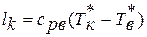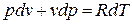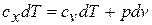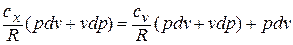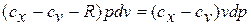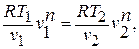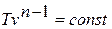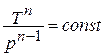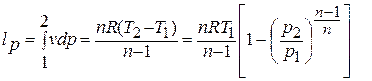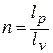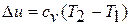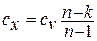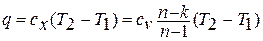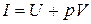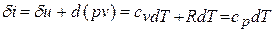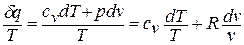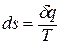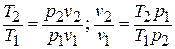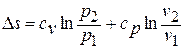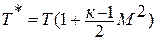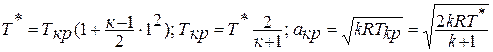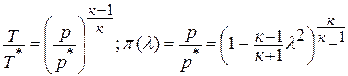Уравнение политропы показатель политропы для процессов

Видео:30. Политропические процессыСкачать

Политропный процесс | 20+ важных часто задаваемых вопросов и числовых значений

Видео:Термодинамика Л3.1. Политропический процесс. Термодинамические циклы и КПДСкачать

Content

Видео:О.Я. Савченко 5.6.28* | Вывод уравнения политропыСкачать

Политропный процесс

Видео:Обобщение политропных процессовСкачать

Определение политропный процесс

Видео:Адиабатный процесс. 10 класс.Скачать

Политропное уравнение | Политропное уравнение состояния

Политропный процесс можно определить уравнением

показатель степени n называется индексом политропы. Он зависит от материала и варьируется от 1.0 до 1.4. Это метод постоянной удельной теплоемкости, при котором учитывается поглощение тепла газом из-за повышения температуры на единицу.

Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Политропный индекс

• п nd закон термодинамики. Эти частные случаи используются в тепловом взаимодействии для астрофизики и химической энергии.
• п = 0: Р = С: Представляет собой изобарический процесс или процесс постоянного давления.
• n = 1: PV = C: Согласно предположению об идеальном газовом законе, PV = C представляет постоянную температуру или изотермический процесс.
• 1 0). Как и в циклах сжатия пара, тепло теряется в горячее окружение.
• п = γ: В предположении закона идеального газа, представляет собой постоянную энтропию, изэнтропический процесс или обратимый адиабатический процесс.
• γ st закон термодинамики,

Видео:Основы теплотехники. Термодинамические процессы. Изохорный, изобарный, изотермический, адиабатный.Скачать

Политропный против изэнтропического процесса

Политропный процесс — это термодинамический процесс, который подчиняется уравнению

Этот процесс учитывает потери на трение и фактор необратимости процесса. Это реальный процесс, за которым следует газ в определенных условиях.

Изэнтропический процесс, также известный как обратимый адиабатический процесс, представляет собой идеальный процесс, в котором не происходит передача энергии или тепла через границы системы. В этом процессе предполагается, что система имеет изолированную границу. Т.к. теплопередача равна нулю. дQ = 0

Согласно первому закону термодинамики,

Видео:Политропный процессСкачать

Политропный процесс против адиабатического процесса

Политропный процесс — это термодинамический процесс, который подчиняется уравнению

Этот процесс учитывает потери на трение и фактор необратимости процесса. Это реальный процесс, за которым следует газ в определенных условиях.

Адиабатический процесс — это особое и специфическое состояние политропного процесса, при котором.

Подобно изэнтропическому процессу, в этом процессе также не происходит передачи энергии или тепла через границы системы. В этом процессе предполагается, что система имеет изолированную границу.

Видео:Политропический процессСкачать

Политропная эффективность

«Политропический КПД, точно определяемый как отношение идеальной работы сжатия для изменения перепада давления в многоступенчатом компрессоре к фактической работе сжатия при изменении перепада давления в многоступенчатом компрессоре».

Проще говоря, это изоэнтропическая эффективность процесса для бесконечно малой ступени многоступенчатого компрессора.

Где, γ = индекс адиабаты

P_d = Давление нагнетания

P_s = Давление всасывания

T_d = Температура подачи

T_s = Температура всасывания

Видео:ЧК_МИФ_ФМЛ_30 _ 2_2_5_3. ПОЛИТРОПНЫЕ ПРОЦЕССЫСкачать

Политропная голова

Политропный напор можно определить как напор, создаваемый центробежным компрессором при политропном сжатии газа или воздуха. Величина развиваемого давления зависит от плотности сжатого газа, и это зависит от изменения плотности газа.

γ = индекс адиабаты

z_{средний} = Средний коэффициент сжимаемости

η = политропная эффективность

P_d = Давление нагнетания

P_s = Давление всасывания

S = удельный вес газа

T_s = Температура всасывания

Видео:29. Адиабатический процесс. Уравнение ПуассонаСкачать

Политропный процесс для воздуха | Политропный процесс для идеального газа

Считается, что воздух является идеальным газом, и поэтому законы идеального газа применимы к воздуху.

………………………. Соотношение между давлением [P] и объемом [V]

………………………. Связь между объемом [В] и температурой [Т]

………………………. Связь между давлением [P] и температурой [T]

Видео:Приемы решения термодинамических задач. Политропа и адиабата. Логарифмические координаты.Скачать

Примеры политропных процессов

Видео:Лекция №7. ТЕРМОДИНАМИЧЕСКИЕ ПРОЦЕССЫ ИДЕАЛЬНЫХ ГАЗОВСкачать

1. Рассмотрим политропный процесс с индексом политропы. п = (1.1). Начальные условия: P₁ = 0, В₁ = 0 и заканчивается на P₂= 600 кПа, В₂ = 0.01 м 3 . Оцените проделанную работу и теплоотдачу.

Ответ: Работы, выполненные политропным процессом, предоставлены

Теплопередача определяется выражением

Видео:Консультация по термодинамике. Часть 1. Билеты 1-10Скачать

2. Поршневой цилиндр содержит кислород при 200 кПа объемом 0.1 м. 3 и при 200 ° С. Масса добавляется так, чтобы газ сжимался с PV. 1.2 = постоянная до конечной температуры 400 ° C. Подсчитайте проделанную работу.

Ответ: Выполненная политропная работа определяется

Видео:Интенсив "Физтех за месяц" | Термодинамика - 1Скачать

3. Рассмотрим аргон при 600 кПа, 30 ° C, сжатый до 90 ° C в политропном процессе с n = 1.33. Найдите проделанную работу на Газе.

Ответ: Выполненная политропная работа определяется

для аргона при 30 ° C составляет 208.1 Дж / кг. K

Принимая m = 1 кг

Видео:Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

4. Предположим, что масса 10 кг ксенона хранится в баллоне при 500 К, 2 МПа, расширение представляет собой политропный процесс (n = 1.28) с конечным давлением 100 кПа. Посчитайте проделанную работу. Учтите, что система имеет постоянную удельную теплоемкость.

Ответ: Выполненная политропная работа определяется

для ксенона при 30 ° C — 63.33 Дж / кг. K

Принимая m = 10 кг

Видео:Лекция №2 "Второе начало термодинамики"Скачать

5. Рассмотрим цилиндр-поршень с начальным объемом 0.3, содержащий 5 кг газообразного метана при давлении 200 кПа. Газ сжимают политропно (n = 1.32) до давления 1 МПа и объема 0.005. Рассчитайте теплопередачу во время процесса.

Ответ: Политропная теплопередача определяется

Видео:Термодинамика Л3. 2022. Изопроцессы. Политропический процесс. Вращательные степени свободыСкачать

6. Примите во внимание цилиндр-поршень, содержащий 1 кг метана при 500 кПа, 20 ° C. Газ политропно сжимают до давления 800 кПа. Рассчитайте теплопередачу с показателем n = 1.15.

Ответ: Политропная теплопередача определяется

Мы знаем, что R для метана = 518.2 Дж / кг. K

Видео:Физический кружок: термодинамика, задачи | Третье занятиеСкачать

7. 1 кг гелия хранится в системе поршень-цилиндр при 303 К, 200 кПа сжимается до 400 К в обратимом политропном процессе с показателем степени n = 1.24. Гелий является идеальным газом, поэтому удельная теплоемкость будет фиксированной. Найдите работу и теплопередачу.

Ответ: Выполненная политропная работа определяется

R для гелия составляет 2077.1 Дж / кг.

Политропная теплопередача определяется выражением

Видео:Урок 178. Тепловые двигатели и их КПД. Цикл КарноСкачать

8. Предположите, что воздух хранится в баллоне объемом 0.3 литра при 3 МПа, 2000 К. Воздух расширяется в соответствии с обратимым политропным процессом с показателем степени n = 1.7, объемное соотношение в этом случае составляет 8: 1. Рассчитайте политропную работу для процесса и сравните ее с адиабатической работой, если процесс расширения следует за обратимым адиабатическим расширением.

Ответ: Нам дается

Соотношение между давлением [P] и объемом [V]

Выполненная политропная работа определяется выражением

Проделанная адиабатическая работа определяется выражением

Для процесса расширения Работа, выполняемая посредством обратимого адиабатического процесса, больше, чем Работа, выполняемая посредством обратимого политропного процесса.

9. В закрытом контейнере содержится 200 л газа при 35 ° C, 120 кПа. Газ сжимается в политропном процессе до температуры 200 ° C, 800 кПа. Найти политропную работу, совершаемую воздухом для n = 1.29.

Ответ: соотношение между давлением [P] и объемом [V]

Выполненная политропная работа определяется выражением

10. Масса 12 кг газообразного метана при 150 ° C, 700 кПа подвергается политропному расширению с n = 1.1 до конечной температуры 30 ° C. Найти теплопередачу?

Ответ: Мы знаем, что R для метана = 518.2 Дж / кг. K

Политропная теплопередача определяется выражением

11. Узел цилиндр-поршень содержит R-134a при 10 ° C; объем 5 литров. Охлаждающая жидкость сжимается до 100 ° C, 3 МПа в соответствии с обратимым политропным процессом. рассчитать проделанную работу и теплоотдачу?

Ответ: Мы знаем, что R для R-134a = 81.49 Дж / кг. K

Выполненная политропная работа определяется выражением

Политропная теплопередача определяется выражением

12. Является ли политропный процесс изотермическим по своей природе?

Ответ: Когда n становится 1 для политропного процесса: согласно предположению об идеальном газовом законе, PV = C представляет постоянную температуру или изотермический процесс.

13. Обратим ли политропный процесс?

Ответ: политропные процессы внутренне обратимы. Вот несколько примеров:

п = 0: Р = С: Представляет собой изобарический процесс или процесс постоянного давления.

n = 1: PV = C: Согласно предположению об идеальном газовом законе, PV γ = C представляет собой постоянную температуру или изотермический процесс.

п = γ: В предположении закона идеального газа, представляет собой постоянную энтропию, изэнтропический процесс или обратимый адиабатический процесс.

n = Бесконечность: Представляет собой изохорный процесс или процесс постоянного объема.

14. Адиабатический политропный процесс?

Ответ: когда п = γ: В предположении закона идеального газа PV γ = C, представляет постоянную энтропию или изэнтропический процесс или обратимый адиабатический процесс.

14. Что такое политропная эффективность?

Ответ: Политропический КПД можно определить как отношение идеальной работы сжатия к фактической работе сжатия при изменении перепада давления в многоступенчатом компрессоре. Проще говоря, это изоэнтропическая эффективность процесса для бесконечно малой ступени многоступенчатого компрессора.

Проще говоря, это изоэнтропическая эффективность процесса для бесконечно малой ступени многоступенчатого компрессора.

Где, γ = индекс адиабаты

P_d = Давление нагнетания

P_s = Давление всасывания

T_d = Температура подачи

T_s = Температура всасывания

15. Что такое гамма в политропном процессе?

Ответ: В политропном процессе, когда п = γ: В предположении закона идеального газа PV γ = C, представляет постоянную энтропию или изэнтропический процесс или обратимый адиабатический процесс.

16. что такое политропный процесс?

Ответ: Политропный процесс можно определить уравнением

показатель степени n называется индексом политропы. Он зависит от материала и варьируется от 1.0 до 1.4. Его также называют процессом с постоянной удельной теплотой, при котором тепло, поглощаемое газом, учитываемое из-за повышения температуры на единицу, является постоянным.

17. Какие выводы можно сделать для политропного процесса с n = 1?

Ответ: когда п = 1: PV n = C : Согласно предположению об идеальном газе, закон становится PV = C представляет собой постоянную температуру или изотермический процесс.

18. Что такое неполитропный процесс?

Ответ: Политропный процесс можно определить уравнением PV n = C показатель степени n называется индексом политропы. Когда,

1. п 0). Как и в циклах сжатия пара, тепло теряется в горячее окружение.
2. п = γ: В предположении закона идеального газа PV γ = C представляет постоянную энтропию или изэнтропический процесс или обратимый адиабатический процесс.
3. γn0). Как и в циклах сжатия пара, тепло теряется в горячее окружение. Изменение температуры происходит из-за изменения внутренней энергии, а не подводимого тепла. Произведенная работа превышает количество поданного или добавленного тепла. Таким образом, даже если при политропном расширении добавляется тепло, температура газа снижается.

21. В политропном процессе, когда PV n = константа, температура тоже постоянна?

Ответ: В политропном процессе, когда PV n = постоянная, температура остается постоянной только при показателе политропы n = 1. Для n = 1: PV = C: Согласно предположению об идеальном газовом законе, PV = C представляет постоянную температуру или изотермический процесс.

Политропный процесс

Политропный процесс

• Обычно фактический процесс работы теплового двигателя происходит при наличии теплообмена, р, в, Т изменений. То есть он не является теплоизолирующим, изобарическим, изобарическим или изотермическим. Для расчета такого процесса соотношение между давлением и объемом обычно выражается уравнениями вида ФВ plvlj p1v Конст. 5. 37. Процесс в соответствии с этим уравнением называется. Политолог. Показатель степени уравнения p НИИ называется политропным indicator. В некоторых процессах величина n постоянна, но в разных процессах политропный показатель может принимать любое число.

Для идеального газа по уравнению pv-rt можно найти уравнение политропного процесса, соединив параметры t, t и t, p. Для этого нужно заменить давление или объем в уравнении 5. 37 соответственно и выразить их с помощью уравнения Клапейрона. После преобразования получены следующие уравнения политропного процесса tv — — t — t2v — const 5. 38 5. 39 ТП т п t2p2. Уравнение 5. 37 5. 38 5. 39 поэтому связь между параметрами в начале и конце политропного процесса может быть легко получена. −1 5.

Поскольку уравнение (16-7) должно быть справедливо также и для воздуха, то одновременно с потоком частиц пара должен существовать и поток частиц воздуха, но в обратном направлении. Людмила Фирмаль

Сорок два. При изучении фактического процесса необходимо установить, является ли процесс политропой, и определить значение индекса политропы. Обычно при изучении работы тепловых машин двигателей, компрессоров и др. , давление и объем рабочей жидкости измеряются в процессе расширения и сжатия. По результатам таких измерений можно построить зависимость p f v рис. 5. 10.

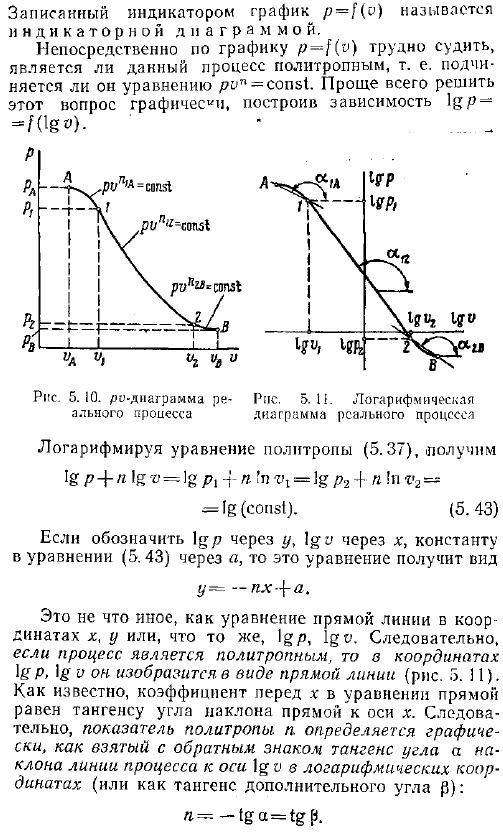
При исследовании работы поршневой машины двигателя внутреннего сгорания, компрессора и др. , такой график рисуют приборы так называемые индикаторы, которые автоматически измеряют изменения давления и объема. Графика р о описывается индикатор называется индикаторной диаграммы. Из графика p-f v трудно непосредственно определить, является ли этот процесс политропой, то есть следует уравнению pon const. Проще всего решить эту проблему графически, построив зависимость lg fog —. — Логарифм уравнения политропа 5. 37, ig p 4-n log-o g pi-i- to r 1 ig p2 4-n in v2— ИГ константа. 5. 43 Если igp обозначается через y, а igo-через x, а константа уравнения 5.

Через a, то это уравнение принимает вид В j -зл-Н. Это то же самое, что и линейные уравнения координат x, y или igp, lgv. So, если процесс представляет собой политропу, то она рисуется в виде прямой линии, с координатами igp, ig рис. 5. 11. Как известно, коэффициент x в уравнении прямой линии равен касательной наклона линии к оси x-axis. As в результате политропный индекс n определяется как тангенс угла a от противоположного знака в логарифмических координатах и как наклон технологической линии к оси МПО или как тангенс дополнительного угла Как будет определено. Обратите внимание, что не все процессы являются политропами.

Например, вы можете видеть, что только процесс at 5. 11, раздел 1-2 процесса at2b, можно считать политропой с равными показателями. Л12 — tga12. Если в координатах лгп фактический процесс МПО не представлен прямой линией, то он разбивается на короткие отрезки, в которых линия практически заменяется прямой segment. In примерный рисунок, раздел 5. 11, al n 2b, также можно считать политропой с индексами n, равными n a — tg u1a и 2b — tg g2b. — Если известно, что процесс является политропным, то значение показателя n можно определить по формуле 2 из значения параметра газа в любой точке этого процесса 5. 43.

Выражает давление по объему из Формулы 3. 2, формулы 5. 37. Эта формула такая же по форме, как и соответствующая формула для процесса термоизоляции, отличающаяся только обозначением индекса теплопроводности. Volume. So, в результате интегрирования вы получите формулу, аналогичную форме 5. Сорок семь Из уравнения состояния pioi этих выражений можно заменить на rt. Выполнив такую замену в выражении 5.

• Мы получим другое выражение, для которого работает политропный процесс. 4 — Г2. 5. 48. Теплотворная способность политропного процесса определяется по следующей формуле 5. 49 Вот, Джей Кг-град — это теплоемкость газа в политропном процессе, то есть процессе, в котором n является постоянной величиной. Теплоемкость газа политропного процесса определяется по общей формуле 4. 3. Для этого необходимо подставить отношение изменения объема к изменению температуры в политропном процессе. Эта зависимость получается путем дифференцирования уравнения 5. 41 политропного процесса переменной Г, о. После логарифма формулы 5.

Отсюда л-т л-1. Подставляя это выражение в выражение 4. 3, вы получаете Если привести их к общему знаменателю с круглыми скобками, то получится формула для теплоемкости газа в политропном процессе. Из этой формулы видно, что было решено учитывать удельную теплоту независимо от температуры удельная теплота идеального газа в политропном процессе будет постоянной. В отличие от теплоемкости cp и c, теплоемкость газа в политропном процессе может быть отрицательной. Это тот случай, когда значение индекса политропа n больше 1 и меньше k, то есть k n.

Так как массосодержание водяного пара иц и воздуха составляют в сумме единицу, градиент массосодержания пара соответствует градиенту маососодержания воздуха. Людмила Фирмаль

Отрицательная теплоемкость означает, что, несмотря на подвод тепла к газу, температура снижается, а при отводе тепла, наоборот, он становится горячим. Это, казалось бы, аномальное поведение температуры объясняется тем, что политропный процесс 1 l, а следовательно, cn 0, получается сильным расширением с небольшим запасом heat. In кроме того, это ln qn, и изменение внутренней энергии отрицательно. Л Несмотря на то, что тепло подается 1 0, когда внутренняя энергия газа уменьшается, температура уменьшается.

В процессе сжатия, если из рабочего тела удаляется меньше тепла, чем выполняется работа, то есть и В случае n избыточная энергия — qn увеличивает внутреннюю энергию газа, и температура повышается. Тепло удаляется н 0. Подставляя давление, выраженное в объеме по уравнению 3. 14 5. 37, показано, что работа газа, имеющаяся в политропном процессе, в n раз больше работы расширения в этом процессе, как это было сделано в адиабатическом процессе 5. 51 Рассмотренные ранее процессы изометрический, изобарный, изотермический, адиабатический-это частный случай политропного процесса. Каждое уравнение может быть представлено в виде swarm const со своим значением индикатора.

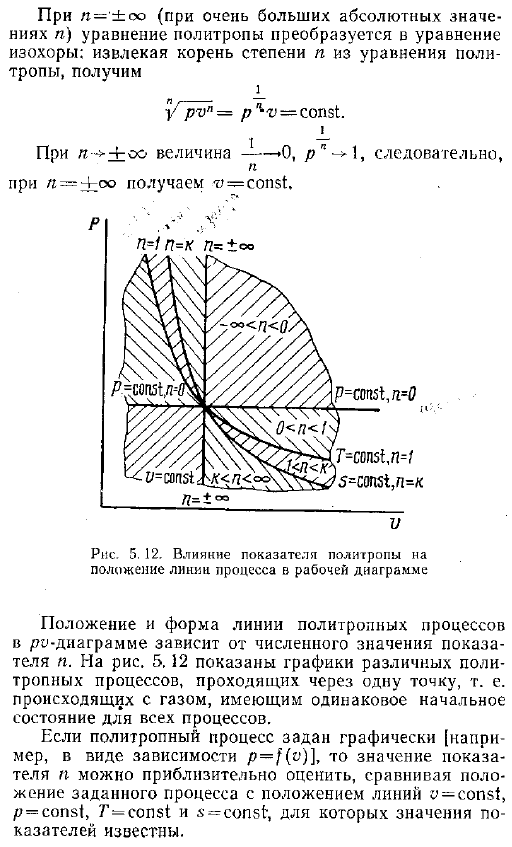
Фактически, в n-0 уравнение политропа принимает следующий вид pr 0 p-1 const или p const изобарный процесс. Если l 1, то политропное уравнение представляет собой изотермический процесс. Рv const и если l a, то политропы соответствуют адиабату. Роль const. В случае n- co где абсолютное значение n очень велико политропное уравнение преобразуется в однородное уравнение. Извлечение корней Порядка n из политропного уравнения дает ПВН Р v пост. Для n — oo значение равно −0 например — — — Лоо, вы получите.

Процесс работы диаграммы расположение и форма линии RO-диаграммы политропного процесса зависит от порядкового номера изделия .На рисунке 5 .12 показан график различных политропных процессов, проходящих через 1 точку .То есть все процессы протекают в одном и том же начальном состоянии газа .Если политропный процесс задан графически например, в виде зависимости p f o, то значение показателя N аппроксимируется путем сравнения положения данного процесса с положениями линий y const, p const, T const и s const .Значение индикатора известно .На рисунке 5 .12 показано ограничение на значение N в политропы между соответствующими линиями этих процессов .Чем выше абсолютное значение показателя, тем круче линия политропного процесса .Рис .

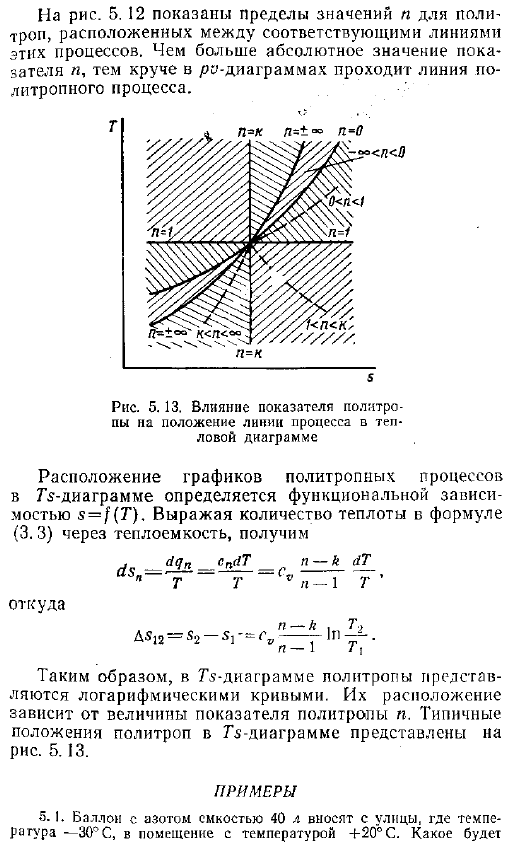
Влияние индекса политропа на расположение технологической линии на диаграмме горячей проволоки Положение графика политропного процесса на диаграмме G определяется зависимостью функции s T .Если величина теплоты уравнения 3 .3 выражается в терминах удельной теплоты, то она выглядит следующим образом Откуда AS12 С2-с — сі, — г п г — Таким образом, в схеме ТС, политроп представлены логарифмические кривые .Их расположение зависит от величины политропного показателя n .на рисунке показано типичное положение политроп на диаграмме G .5 .13 .Пример 5 .1 .Возьмите баллон с емкостью 40 литров азота с улицы, где температура составляет −3 C, в помещение с температурой 20 C .Давление в баке и температура азота равны давлению в баке 98 dir Тепло, и равное cv 742 Дж Кг-град .Решение .О нагревании шара .- Меняйся, Трейс .— 297 Дж кг град- 2 .7 найти 9810S-0 .04 М ря, 7а-Д 5 .45-742 .10-1 293-243 −202 кДж .

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Уравнение политропного процесса.

Продифференцируем уравнение состояния для 1 кг идеального газа:

Принимая теплоемкость не зависящей от температуры, получим уравнение первого закона термодинамики в дифференциальной форме:

Подставляя в это уравнение выражение для 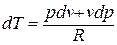, получаем

Разделяя переменные и произведя интегрирование, получаем

,

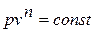
где 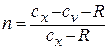— показатель политропы, может принимать значения от нуля до бесконечности.

Зависимость между температурой и удельным объёмом определяется путём замены давления в уравнении политропного процесса его значением из уравнения состояния идеального газа:

или

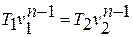
Исключая подобным же образом удельный объём, находим зависимость между давлением и температурой:

отсюда или

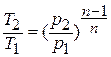
Деформационная работа, производимая 1 кг газа в политропном процессе, определяется по формуле:

Техническая работа, производимая 1 кг газа в политропном процессе, находится по формуле:

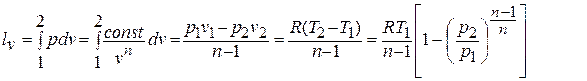
То есть отношение технической и деформационной работ равно показателю политропы:

Изменение внутренней энергии в политропном процессе находится общей формулой:

Теплоёмкость процесса 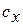определяется из выражения для показателя политропы:

Количество теплоты в политропном процессе находится по формуле:

1.12. Энтальпия рабочего тела.

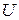
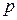
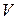
В термодинамике важную роль играет сумма внутренней энергии системы и произведения давления системы на её объём , называемая энтальпией или теплосодержанием и обозначаемая I или Н:

Так как входящие в нее величины являются функциями состояния, то и сама энтальпия является функцией состояния.

Так же как внутренняя энергия, работа и теплота, она измеряется в джоулях (Дж).

Энтальпия обладает свойством аддитивности . Величина

называемая удельной энтальпией ( 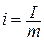), представляет собой энтальпию системы, содержащей 1 кг ве­щества, и измеряется в Дж/кг.

Поскольку энтальпия есть функция состояния, то она может быть представ­лена в виде функции двух любых пара­метров состояния:

, а величина di является полным

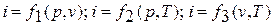
Изменение энтальпии в любом про­цессе определяется только начальным и конечным состояниями тела и не за­висит от характера процесса.

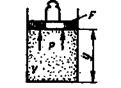
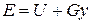
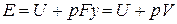
Физический смысл энтальпии выяс­ним на следующем примере. Рассмотрим расширенную систему, включающую газ в цилиндре и поршень с грузом общим весом G (рис.1.7). Энергия этой системы складывается из внутренней энергии га­за и потенциальной энергии поршня с грузом в поле внешних сил: . В условиях равновесия (G = pF) эту функцию можно выразить через па­раметры газа: . Получаем, что , т.е. энтальпию можно трактовать как энергию расширенной системы.

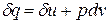
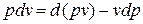
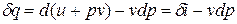
Уравнение в случае, когда единственным видом работы является работа расширения, с уче­том очевидного соотношения может быть записано в виде .

Рис.1.10. К определению физического смысла энтальпии

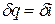
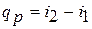
Из этого соотношения следует, что если давление термодинамической системы сохраняется неизменным, то есть осуществляется изобарный процесс (dp = 0), то и , то теплота, подведенная к системе при постоянном давлении, идет только на изменение энтальпии данной системы.

Это выражение очень часто используется в расчетах, так как огромное

количество процессов подвода теплоты в теплоэнергетике (в паровых котлах, камерах сгорания газовых турбореактивных двигателей, теплообменных аппаратах), а также целый ряд процессов химической технологии и многих других производствах осуществляется при постоянном давлении. Кстати, по этой причине в таблицах термодинамических свойств обычно приводятся значения энтальпии, a не внутренней энергии.

Для идеального газа для вычисления энтальпии используется формула

Так как между энтальпией и внутренней энергией существует связь, выбор начала отсчета одной из них произволен: в точке, принятой за начало отсчета внутренней энергии, 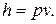Например, для воды при = 0,01 °С ,

р = 610,8 Па, , a .

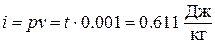
При расчетах практический интерес представляет изменение энтальпии в конечном процессе:

1.13. Энтропия рабочего тела.

Как уже указывалось, величина 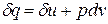не является полным дифференциалом, так как теплота и изменение внутренней энергии зависят от теплоемкости, которая, в свою очередь, является функцией температуры. Кроме того, чтобы проинтегрировать правую часть этого уравнения, нужно знать зависимость давления от удельного объёма, то есть нужно знать процесс, который совершается.

В математике доказывается, что дифференциальный двучлен всегда можно превратить в полный дифференциал путем умножения (или деления) на интегрирующий множитель (или делитель). Таким интегрирующим делителем для элементарного количества теплоты 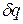является абсолютная температура Т.

Покажем это на примере изменения состояния идеального газа в равновесных процессах:

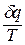
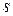
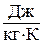
Выражение при равновесном изменении состояния газа есть полный дифференциал некоторой функции состояния, которая называется энтропией, обозначается для 1 кг газа через и измеряется в . Термин «энтропия» был введен впервые Рудольфом Юлиусом Эммануэлем Клаузиусом (1822 – 1888), немецким физиком, в 1865 году.

Для произвольного количества газа энтропия, обозначаемая через ,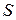

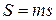
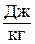
равна и измеряется в .

Таким образом, аналитически энтропия определяется следующим образом:

Эта формула справедлива как для идеальных, так и для реальных газов.

Подобно любой другой функции состояния энтропия может быть представлена в виде функции любых двух параметров состояния:

Понятием «энтропия» (от греч. Entropia – поворот, превращение) будем называть в термодинамике направление теплообмена между рабочим телом термодинамической системы и внешней средой.

Значение энтропии для заданного состояния газа определяется интегрированием уравнения для энтропии:

, где — константа интегрирования.

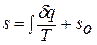
При температурах, близких к абсолютному нулю, все известные газы находятся в конденсированном состоянии. Вальтер Нернст (1864 – 1941), немецкий физик и химик, в 1906 году экспериментально установил, а Макс Планк (1858 – 1947), немецкий физик, в 1912 году окончательно сформулировал следующий принцип:

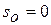
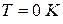
при температуре, стремящейся к абсолютному нулю, энтропия газа, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю,то есть при .

Этот закон называют третьим законом термодинамикиили тепловой теоремой В.Нернста. Он позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии, которые всегда отсчитываются от произвольного уровня.

Однако в технической термодинамике обычно используется не абсолютное значение энтропии, а ее изменение в каком-либо процессе:

(1.18)

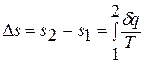
поэтому энтропию тоже отсчитывают от произвольно выбранного уровня.

Получим формулы, позволяющие вычислить изменение энтропии идеального газа. Для этого проинтегрируем уравнение для энтропии, полагая :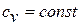

Имея в виду уравнение состояния, записанное для состояний «1» и «2», получаем:

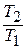
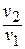
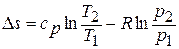
После подстановки отношений и получаем следующие формулы для изменения энтропии идеального газа:

;

Поскольку энтропия есть функция со­стояния рабочего тела, написанными уравнениями можно пользоваться вне зависимости от пути перехода рабочего тела между состояниями «1» и «2» и, в частности, от того, равновесный этот переход или нет.

Понятие энтропии позволяет ввести чрезвычайно удобную для термодинамических расчетов -диаграмму, на которой (как и

на -диаграмме) состояние термодинамической системы изображается точкой, а равновесный термодинамический процесс линией (рис.1.11).

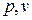
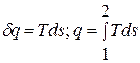
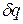
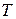
Из уравнения для изменения энтропии следует, что в равновесном процессе: . Очевидно, что в — диаграмме элементарная теплота процесса изображается элементарной площадкой с высотой и основанием ds, а площадь, ограниченная

Рис.1.11. Графическое изображение теплоты в — координатах.

линией процесса, крайними ординатами и осью абсцисс, эквивалентна теплоте процесса.

Формула для элементарного изменения энтропии показывает, что и имеют одинаковые знаки, следовательно, по характеру изменения в равновесном процессе можно судить о том, в каком направлении происходит теплообмен. При подводе теплоты ( ) его энтропия возрастает ( ), а при отводе теплоты ( ) убывает (ds Q, a dT 2 , а отношение скорости к скорости звука называется числом Маха .

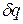
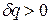
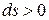
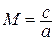
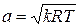
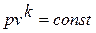
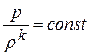
Данное отношение названо в честь Эрнста Маха (1838 – 1916), австрийского физика и философа; отношение является критерием( от греч. Kriterion – средство для суждения) – признаком, на основании которого производится оценка, определение или классификация чего — либо; мерило оценки; в данном случае критерий сжимаемости газа. Формула получается при допущении, что звуковая энергия (волна) распространяется в газе или жидкости в соответствии с уравнением адиабатного процесса или .

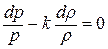
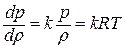
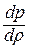
Дифференциальное уравнение этого процесса представляется так , или . Отношение соответствует величине звуковой энергии (квадрату скорости распространения звука в веществе).

Отсюда выражение для полной энергии потока в сечении записывается так:

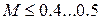
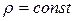
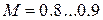
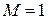
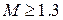
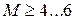
Число Маха, таким образом, является характеристикой сжимаемости рабочего тела. Например, при сжимаемостью газа можно пренебречь и принять , то есть считать газ как жидкость. При — околозвуковой поток, характерный для полетов гражданских самолетов; при — звуковой барьер или критический режим течения потока; при — трансзвуковой поток, характерный режим обтекания некоторых участков крыла самолета даже при околозвуковой скорости полета воздушного судна; при — сверхзвуковой поток; при гиперзвуковой поток. Поскольку плотность воздуха в атмосфере Земли с высотой уменьшается практически до нуля, то число Маха в полете при этих условиях стремится к бесконечности (например, поток газа в пустоту).

Принимая 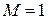, находим критическую скорость звука, используя выражение:

Если формулу для полной энергии потока разделить на и обозначить отношение скорости к критической скорости звука как приведенную скорость , то выражение для полной энергии потока в сечении (или для любой точки потока) представляется так

или — газодинамическая функция температуры. Значение приведенной скорости меняется от нуля до максимального значения .

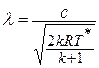
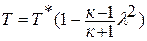
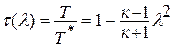
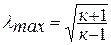
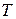
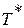
Если принять процесс торможения потока от температуры до адиабатным, что практически соответствует приборам для измерения давления в потоке, то можно найти выражение для газодинамической функции давления

или плотности .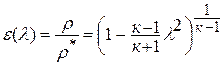

Уравнение сохранения энергии широко используется в авиационной практике для различных элементов двигателей. Например:

а) работа , подводимая к валу ротора компрессора ;