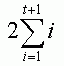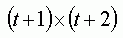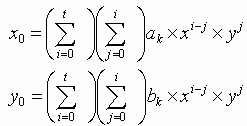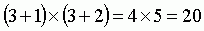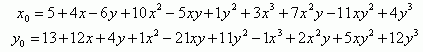Уравнение полиномиального тренда второго порядка (8 видео)

3 способа расчета полинома в Excel.

Автор: Алексей Батурин.

Есть 3 способа расчета значений полинома в Excel:

1-й способ с помощью графика;
2-й способ с помощью функции Excel =ЛИНЕЙН();
3-й способ с помощью Forecast4AC PRO;

Подробнее о полиноме и способе его расчета в Excel далее в нашей статье.

Полиномиальный тренд применяется для описания значений временных рядов, попеременно возрастающих и убывающих. Полином отлично подходит для анализа большого набора данных нестабильной величины (например, продажи сезонных товаров).

Что такое полином? Полином — это степенная функция y=ax 2 +bx+c (полином второй степени) и y=ax 3 +bx 2 +cx+d (полином третей степени) и т.д. Степень полинома определяет количество экстремумов (пиков), т.е. максимальных и минимальных значений на анализируемом промежутке времени.

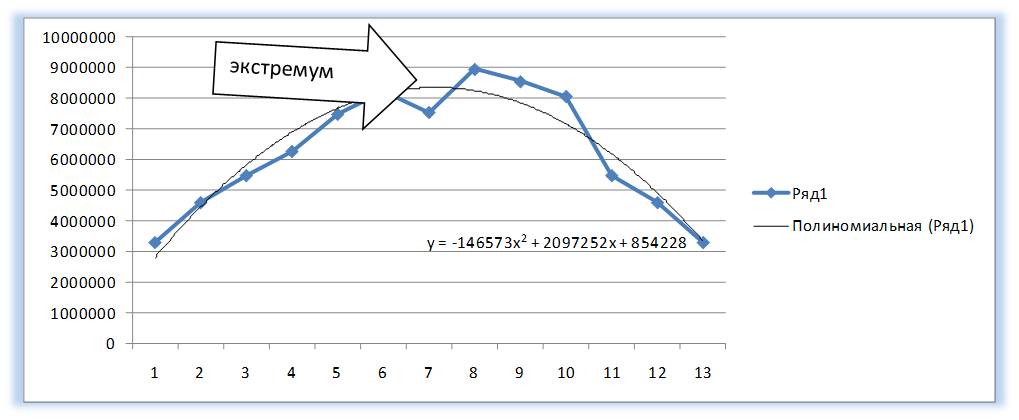
У полинома второй степени y=ax 2 +bx+c один экстремум (на графике ниже 1 максимум).

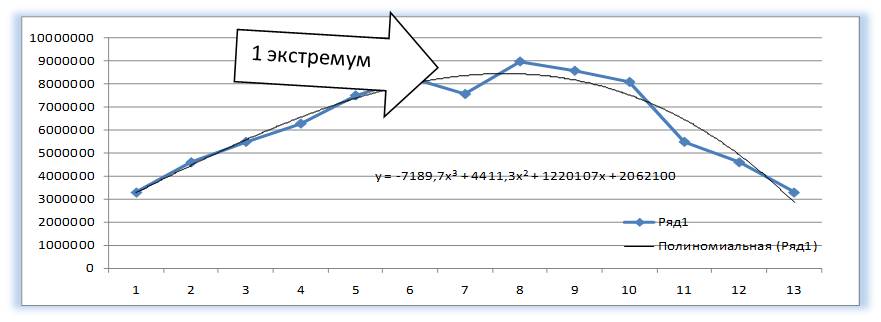
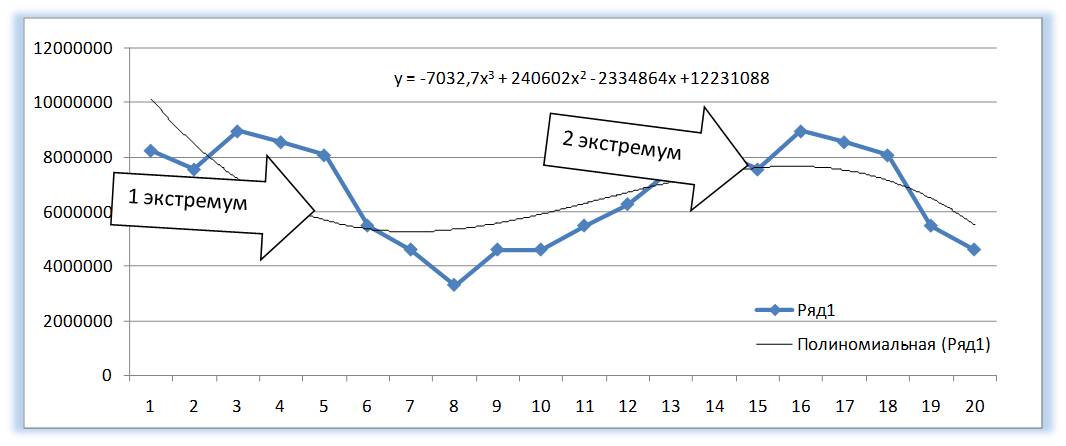
У Полинома третьей степени y=ax 3 +bx 2 +cx+d может быть один или два экстремума.

Один экстремум

Два экстремума

У Полинома четвертой степени не более трех экстремумов и т.д.

Содержание

Как рассчитать значения полинома в Excel?
1-й способ расчета полинома — с помощью графика
2-й способ расчета полинома в Excel — функция ЛИНЕЙН()
3-й способ расчета значений полиномиальных трендов — Forecast4AC PRO
Присоединяйтесь к нам!
GIS-LAB
Полиномиальные преобразования
Доработка алгоритма прогнозирования объема продаж
ПРИМЕР.
🔥 Видео

Видео:16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Как рассчитать значения полинома в Excel?

Есть 3 способа расчета значений полинома в Excel:

1-й способ с помощью графика;
2-й способ с помощью функции Excel =ЛИНЕЙН;
3-й способ с помощью Forecast4AC PRO;

1-й способ расчета полинома — с помощью графика

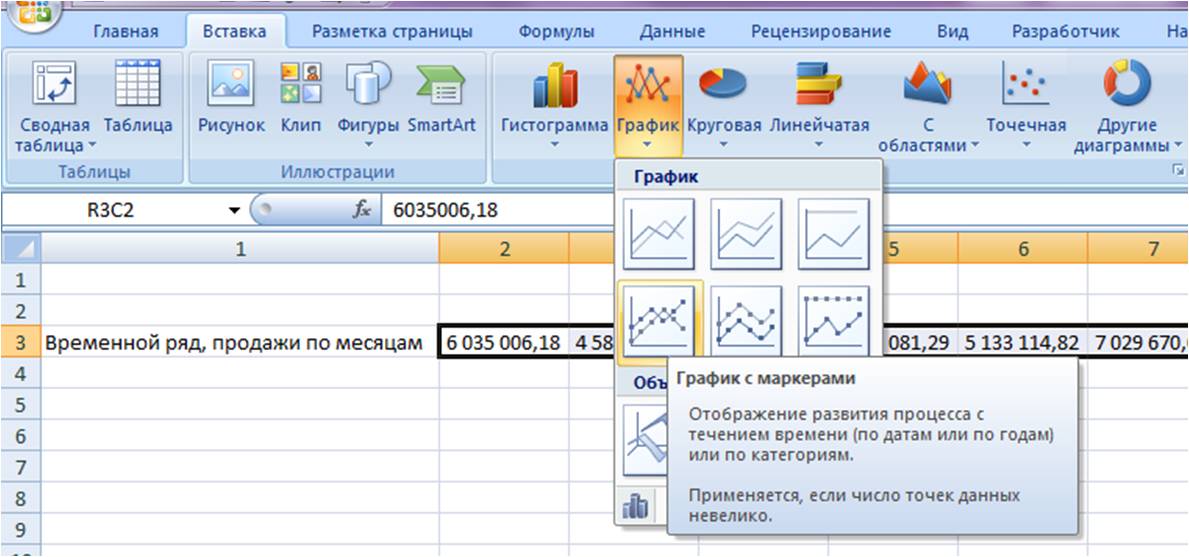
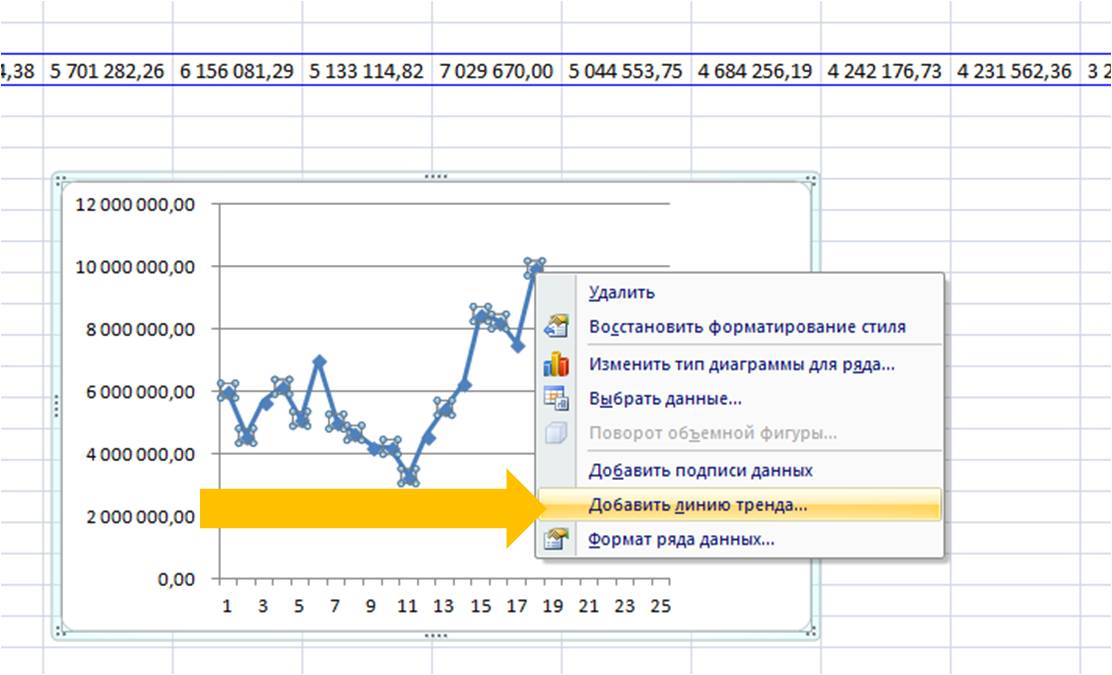
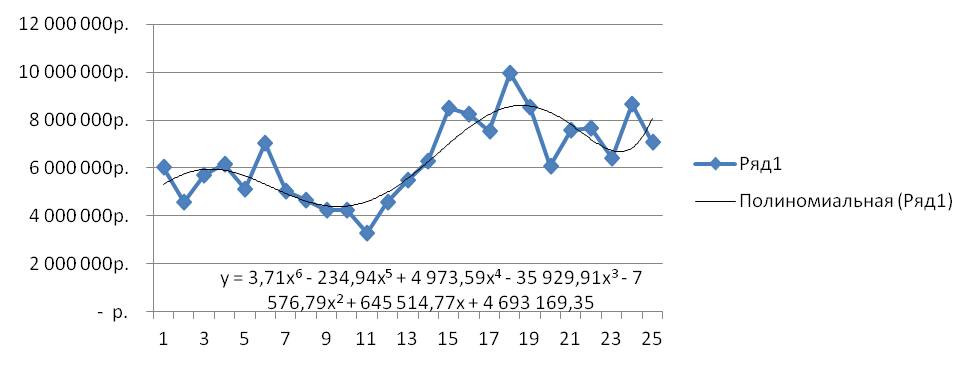
Выделяем ряд со значениями и строим график временного ряда.

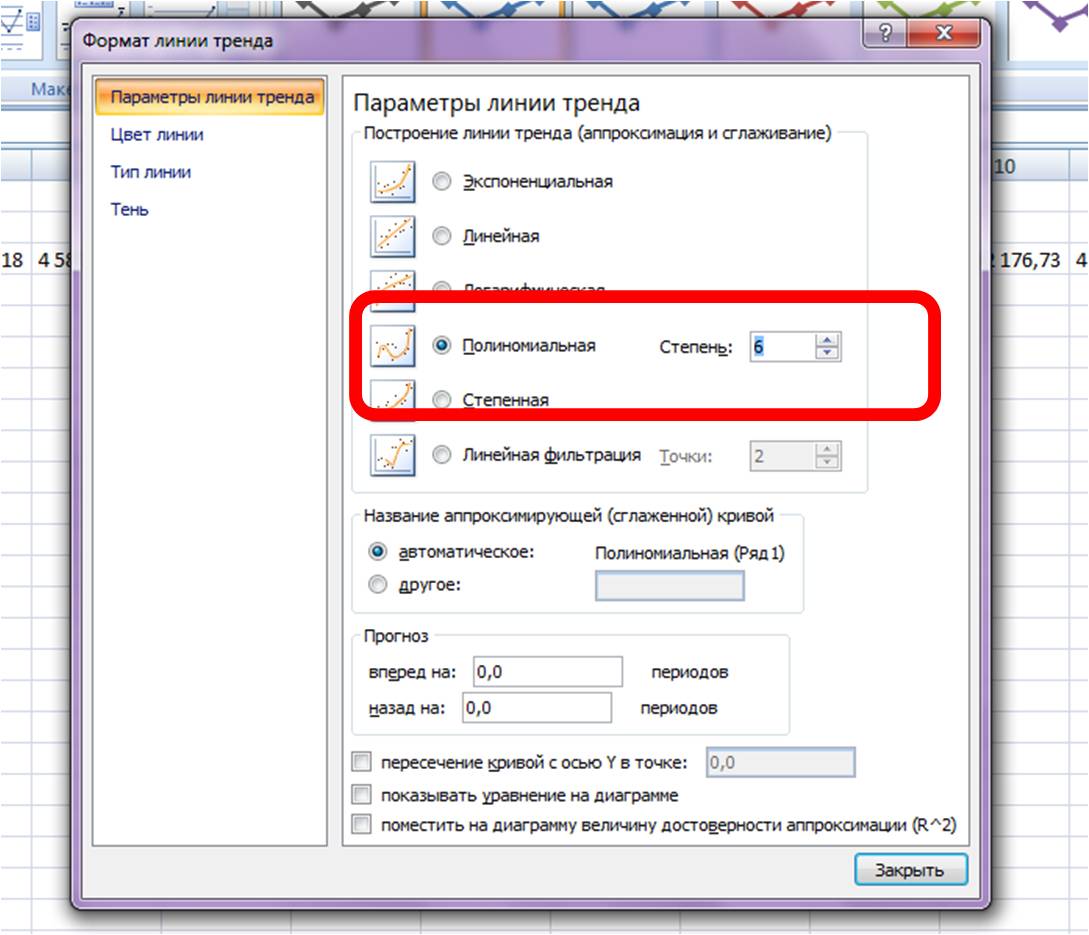
На график добавляем полином 6-й степени.

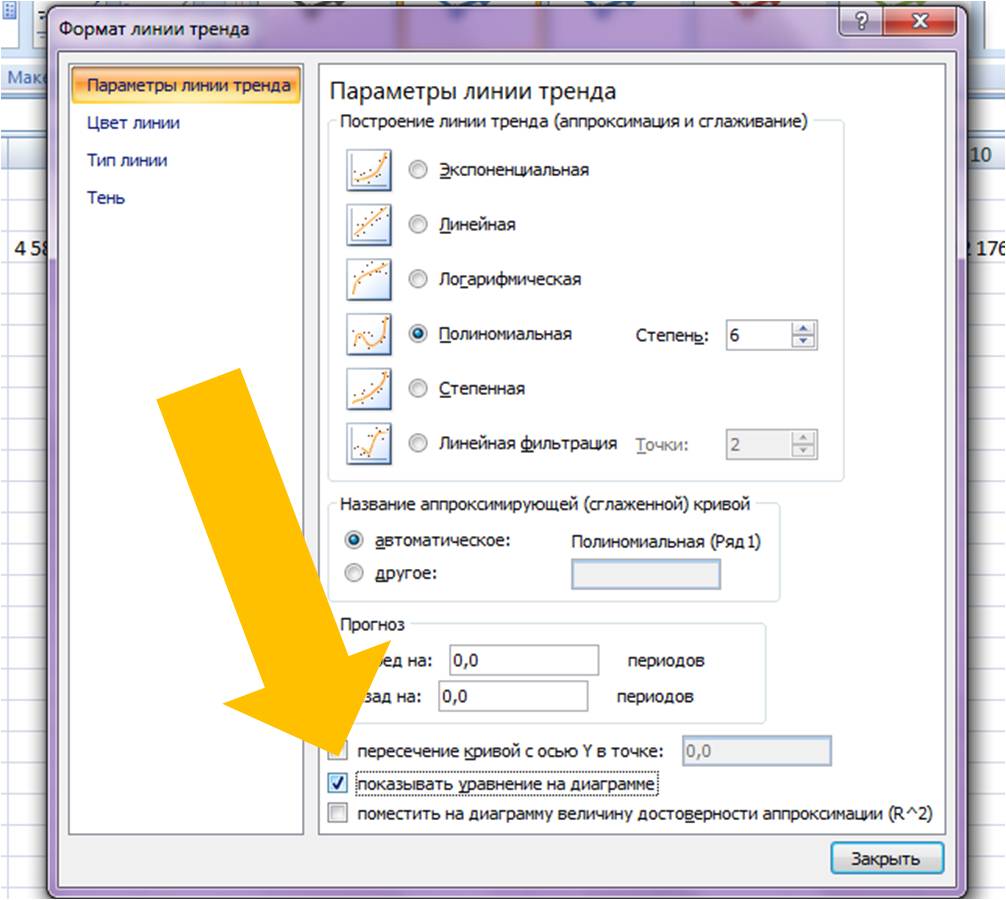
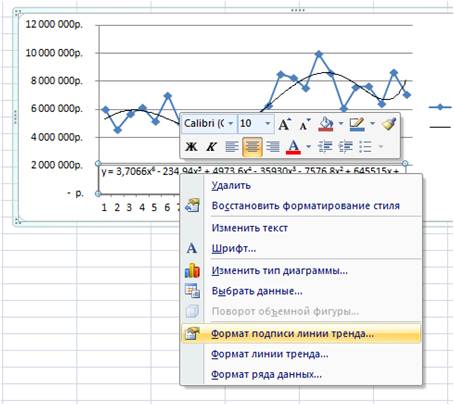
Затем в формате линии тренда ставим галочку «показать уравнение на диаграмме»

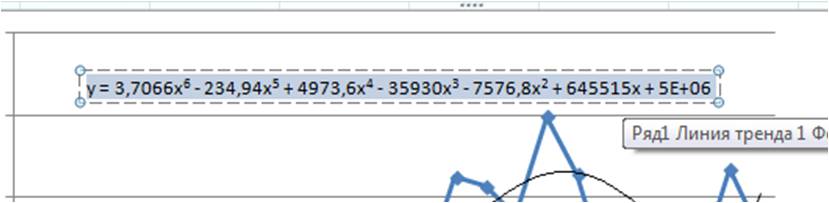
После этого уравнение выводится на график y = 3,7066x 6 — 234,94x 5 + 4973,6x 4 — 35930x 3 — 7576,8x 2 + 645515x + 5E+06 . Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома

Нажимаем правой кнопкой и выбираем «формат подписи линии тренда»

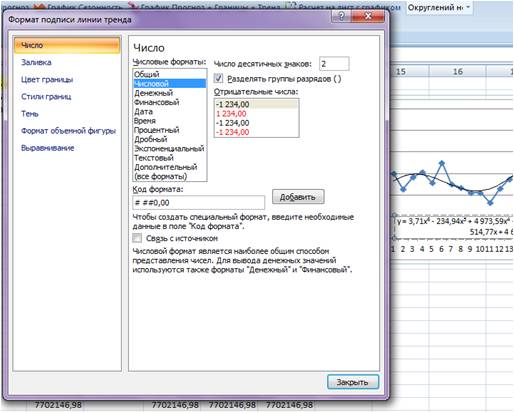
В настройках подписи линии тренда выбираем число и в числовых форматах выбираем «Числовой».

Получаем уравнение полинома в читаемом формате:

y = 3,71x 6 — 234,94x 5 + 4 973,59x 4 — 35 929,91x 3 — 7 576,79x 2 + 645 514,77x + 4 693 169,35

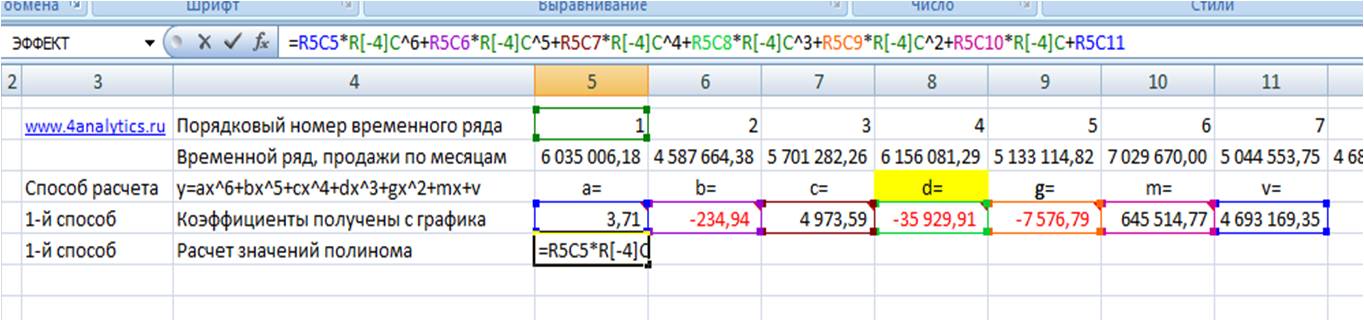
Из этого уравнения берем коэффициенты a, b, c, d, g, m, v, и вводим в соответствующие ячейки Excel

Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение вместо X.

Рассчитаем значения полинома для каждого периода. Для этого вводим формулу полинома y = 3,71x 6 — 234,94x 5 + 4 973,59x 4 — 35 929,91x 3 — 7 576,79x 2 + 645 514,77x + 4 693 169,35 в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)

Получаем формулу следующего вида:

= R2C8 *RC[-3]^6+ R3C8 *RC[-3]^5+ R4C8 *RC[-3]^4+ R5C8 *RC[-3]^3+ R6C8 *RC[-3]^2+ R7C8 *RC[-3]+ R8C8

в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)

Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)

=R2C8*RC[-3] ^6 +R3C8*RC[-3] ^5 +R4C8*RC[-3] ^4 +R5C8*RC[-3] ^3 +R6C8*RC[-3] ^2 +R7C8*RC[-3]+R8C8

Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.

2-й способ расчета полинома в Excel — функция ЛИНЕЙН()

Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel =ЛИНЕЙН()

Для расчета коэффициентов в формулу =ЛИНЕЙН(известные значения y, известные значения x, константа, статистика) вводим:

«известные значения y» (объёмы продаж за периоды),
«известные значения x» (порядковый номер временного ряда),
в константу ставим «1»,
в статистику «0»

Получаем следующего вида формулу:

Теперь, чтобы формула Линейн() рассчитала коэффициенты полинома, нам в неё надо дописать степень полинома, коэффициенты которого мы хотим рассчитать.

Для этого в часть формулы с «известными значениями x» вписываем степень полинома:

^ — для расчета коэффициентов полинома 6-й степени
^ — для расчета коэффициентов полинома 5-й степени
^ — для расчета коэффициентов полинома 2-й степени

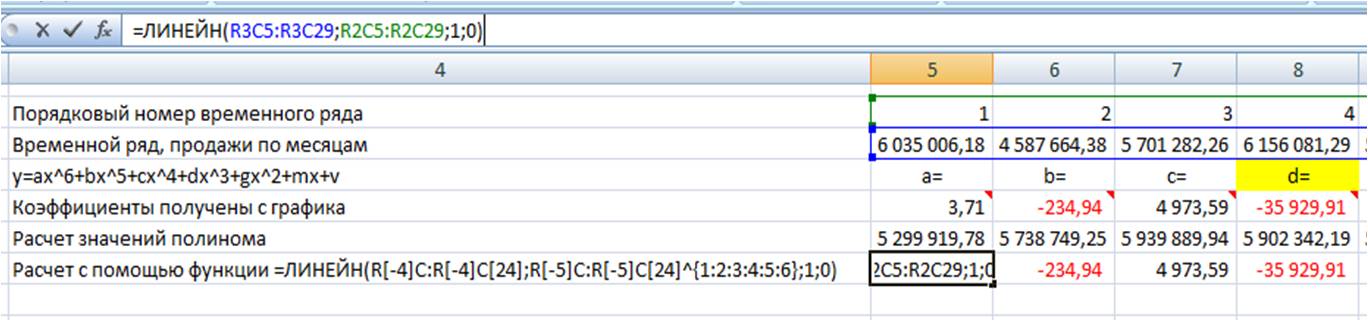
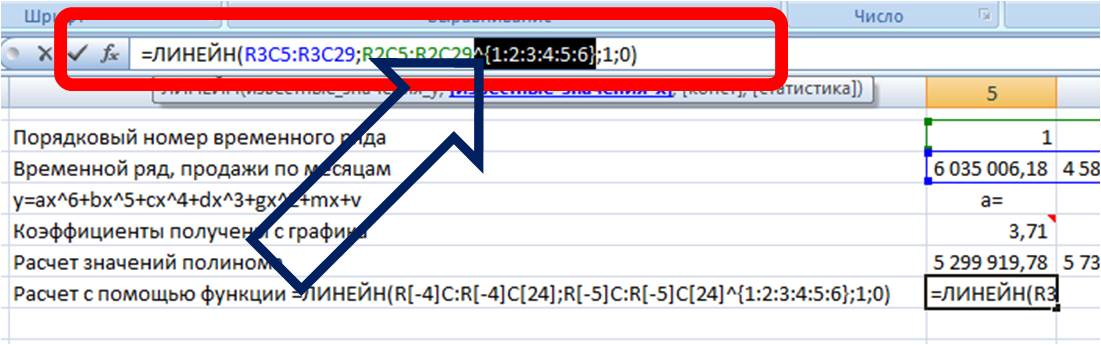
Получаем формулу следующего вида:

Вводим формулу в ячейку, получаем 3,71 —- значение (a) для полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v

Для того, чтобы Excel рассчитал все 7 коэффициентов полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v, необходимо:

1. Установить курсор в ячейку с формулой и выделить 7 соседних ячеек справа, как на рисунке:

2. Нажать на клавишу F2

3. Затем одновременно — клавиши CTRL + SHIFT + ВВОД (т.е. ввести формулу массива, как это сделать читайте подробно в статье «Как ввести формулу массива»)

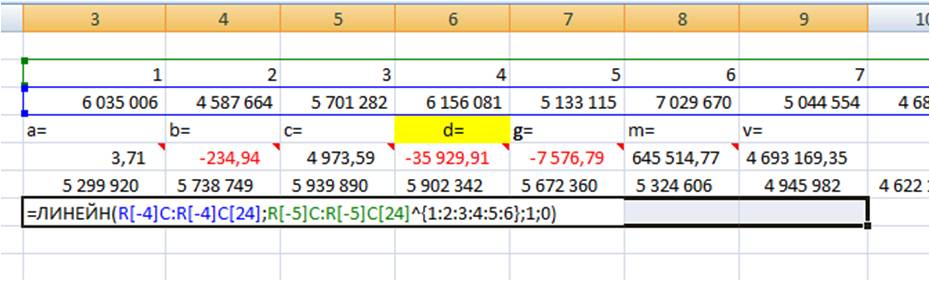
Получаем 7 коэффициентов полиномиального тренда 6-й степени.

Рассчитаем значения полиномиального тренда с помощью полученных коэффициентов. Подставляем в уравнение y=3,7* x ^ 6 -234,9* x ^ 5 +4973,5* x ^ 4 -35929,9 * x^3 -7576,7 * x^2 +645514,7* x +4693169,3 номера периодов X, для которых хотим рассчитать значения полинома.

Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение полинома вместо X.

Рассчитаем значения полиномиального тренда для каждого периода. Для этого вводим формулу полинома в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)

Получаем формулу следующего вида:

= R2C8 *RC[-3]^6+ R3C8 *RC[-3]^5+ R4C8 *RC[-3]^4+ R5C8 *RC[-3]^3+ R6C8 *RC[-3]^2+ R7C8 *RC[-3]+ R8C8

Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)

=R2C8*RC[-3] ^6 +R3C8*RC[-3] ^5 +R4C8*RC[-3] ^4 +R5C8*RC[-3] ^3 +R6C8*RC[-3] ^2 +R7C8*RC[-3]+R8C8

2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также этот расчет быстрее.

3-й способ расчета значений полиномиальных трендов — Forecast4AC PRO

Устанавливаем курсор в начало временного ряда

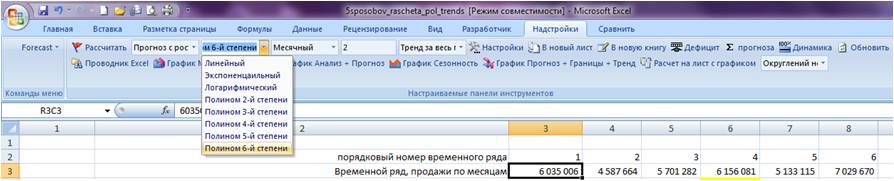
Заходим в настройки Forecast4AC PRO, выбираем «Прогноз с ростом и сезонностью», «Полином 6-й степени», нажимаем кнопку «Рассчитать».

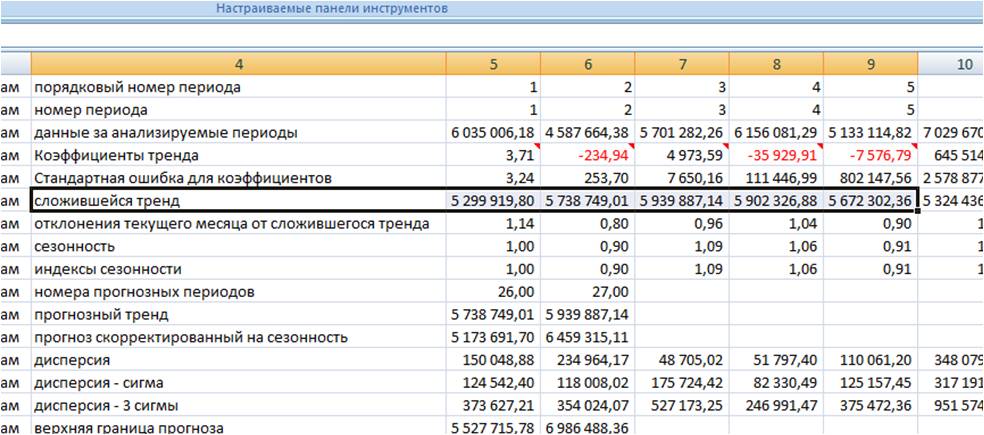
Заходим в лист с пошаговым расчетом «ForPol6», находим строку «Сложившийся тренд»:

Копируем значения в наш лист.

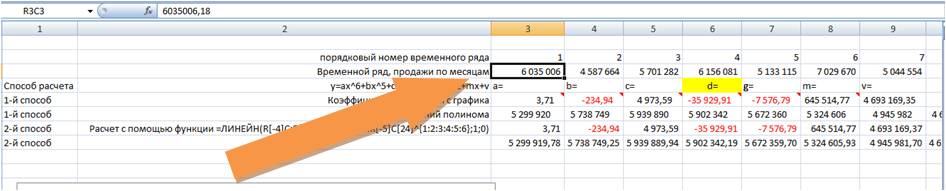
Получаем значения полинома 6-й степени, рассчитанные 3 способами с помощью:

Коэффициентов полиномиального тренда выведенных на график;
Коэффициентов полинома рассчитанных с помощью функцию Excel =ЛИНЕЙН
и с помощью Forecast4AC PRO одним нажатием клавиши, легко и быстро.

Присоединяйтесь к нам!

Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:

Novo Forecast Lite — автоматический расчет прогноза в Excel .
4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.

Тестируйте возможности платных решений:

Novo Forecast PRO — прогнозирование в Excel для больших массивов данных.

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Видео:Прогнозирование в Excel с помощью линий трендаСкачать

GIS-LAB

Географические информационные системы и дистанционное зондирование

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Полиномиальные преобразования

Формулы и примеры расчетов полиномиальных преобразований

Формулы полиноминальных преобразований используются для перевода исходных координат (обычно локальных-прямоугольных) в конечные (обычно спроектированные — прямоугольные). В зависимости от искажения изображения, количества контрольных точек (GCP – ground control point), и их размещения относительно друг друга, для выражения необходимого преобразования могут потребоваться достаточно сложные полиноминальные формулы. Сложность полинома выражается через его порядок. Порядок – это показатель наивысшей степени, используемой в полиноме.

Линейные преобразования

Преобразование 1-го порядка – линейное преобразование. Это преобразование может изменять:

положение по X и/или Y; Изменение положения, смещает изображение на определенное число пикселей по X и Y.
масштаб по X и/или Y; Коэффициенты масштабирования по X и Y могут быть различными
наклон по X и/или Y;
поворот; При повороте, можно определить любое положительное или отрицательное число градусов, для поворота по- и против часовой стрелки соответственно. Поворот происходит вокруг центрального пикселя изображения.
Отражение; слева направо, сверху вниз, сверху вниз и слева направо (аналогично повороту на 180 градусов)

Преобразование 1-го порядка может быть использовано для перевода исходного (например только что отсканированного) изображения в прямоугольную систему координат, преобразования одной прямоугольной системы координат в другую, обычно это преобразование используется для относительной небольших фрагментов.

Примерами применения этого преобразования могут быть: исправление перекосов в данных дистанционного зондирования, поворота отсканированных топографических листов, и поворота данных с нисходящих орбит так, что бы север был вверху изображения (а не по ходу орбиты).

Преобразование 1-го порядка также может быть использовано для данных, которые уже спроецированы на плоскость. Например, часто данные дистанционного зондирования, уже находятся в локальной прямоугольной системе координат, но не приведены к соответствующей проекции. При использовании данного типа преобразования, не имеет смысла увеличение порядка преобразования, если при первом порядке возникает большая среднеквадратическая ошибка. Сначала, необходимо проверить другие возможные источники ошибок: качество опорных точек, их распределение и другие возможные систематические ошибки.

На рисунке показано, как изменяются данные при линейных преобразованиях.

Для осуществления полиномиального преобразования первой степени необходимо найти 6 коэффициентов — по три на каждую координату (X и Y): a₀, a₁, a₂, b₀, b₁, b₂. Эти коэффициенты, далее используются в собственно уравнениях полиномиального преобразования первой степени (эквивалентного также аффинному преобразованию):

где x,y — исходные координаты, x₀,y₀ — конечные координаты

Нелинейные преобразования

Нелинейные преобразования – это преобразования 2-го и более порядка. Эти преобразования могут корректировать нелинейные искажения. На рисунке изображены примеры результатов некоторых нелинейных преобразований.

Преобразования 2-го порядка могут быть использованы для преобразования данных в географической системе координат (широта, долгота) в прямоугольную, для преобразования данных больших областей (для учета кривизны Земли), для точно привязки искаженных по той или иной причине данных (например, из-за искажений линз камеры, плохо отсканированных материалов) и т.д.

Матрица преобразования

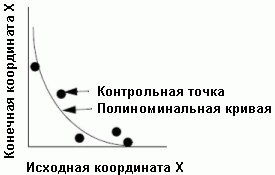
Матрица преобразования рассчитывается по контрольным точкам. Матрица состоит из коэффициентов, которые используются в формулах полиномов для преобразования координат. Размерность матрицы зависит от порядка используемого преобразования. Коэффициенты матрицы преобразований рассчитываются таким образом, чтобы получить формулы полиномиального преобразования с как можно меньшей ошибкой перевода исходных координат в конечные. Получить коэффициенты, которые не приводят к ошибкам удается не всегда. Пример, иллюстрирующий ошибку исходной координаты относительно конечной и кривой, аппроксимирующей зависимость между ними, выраженной полиномом (не все точки лежат на линии, расстояние от исходной точки до кривой полинома — среднеквадратичная ошибка). Для простоты в примере показано только отношение исходной и конечной координаты X и описывающее его кривая, в реальной жизни, исходных координат 2 и конечных координат 2, поэтому зависимость между ними аппроксимируется не кривой, а плоскостью.

Количество коэффициентов матрицы преобразований для преобразования порядка t равно:

Это число необходимо умножить на 2 – для двух наборов коэффициентов, один — для X, другой для Y. Более простая формула для получения количества коэффициентов:

Очевидно, что размерность матрицы преобразований увеличивается с ростом порядка преобразования, соответственно минимальное количество контрольных точек необходимых для вычислений коэффициентов матрицы тоже растет.

Каждая контрольная точка влияет на расчетные коэффициенты, если нет идеального соответствия каждой контрольной точки полиному, который представлен этими коэффициентами. Расстояние между кривой и расчетной координаты точки – называется ошибкой RMS (среднеквадратической ошибкой точки). Для расчета матрицы преобразований по набору контрольных точек используется метод среднеквадратической регрессии (метод наименьших квадратов) на основе контрольных точек расставляемых пользователем от исходного (привязываемого) материала, к конечному материалу (тому, к которому привязывают).

Формула вычисления полинома порядка t

Где: t – порядок полинома, a_k и b_k – коэффициенты, индекс k для a_k и b_k вычисляется как:

Например, для преобразования 3-го порядка будет использоваться 20 коэффициентов:

Формула для преобразования 3-го порядка, после вычисления коэффициентов, может выглядеть так:

Влияние порядка преобразования

Расчет формул полиномов высоких порядков и выходных значений сложнее, чем расчет полиномов первых порядков. Поэтому, полиномы высоких порядков применяются для изображений требующих для привязки более сложных искажений. Для понимания влияния различных порядков преобразования при спрямлении изображения, полезно рассмотреть выходные величины полиномов различных порядков.

В следующем примере, для просты, используется только одна координата (X), вместо двух (X, Y), которые для расчетов в полиномиальных преобразованиях. Это позволяет использовать двухмерные графики, иллюстрирующие, как использование преобразования определенного порядка позволяет связать исходные и конечные координаты. Из-за того, что в примере используется только координата X, число используемых контрольных точек меньше реально требуемого для преобразований соответствующих порядков.

Коэффициенты, подобные тем, которые использованы в примере, обычно рассчитываются по методу наименьших квадратов. Предположим, что введены следующие контрольные точки:

Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Доработка алгоритма прогнозирования объема продаж

Столкнувшись с методикой предложенной Кошечкиным С.А., был крайне признателен автору, поскольку аналогичных материалов не так уж и много. Особенно интересно было изучение сезонных колебаний автором статьи, т.к. предприятие, работником которого я являюсь, продает самый что ни на есть сезонный товар – строительные материалы.

Методики простого и в то же время адекватного прогнозирования на сегодняшний день действительно освещены в научных материалах в небольшом количестве. Одни просты до такой степени, что моделируют ситуацию крайне далекую от реальной. А другие настолько сложны, что период их применения и сбора необходимой информации значительно превышает все установленные начальством сроки.

Методика, предложенная Кошечкиным С.А., сочетает в себе и простоту, и адекватность анализа. Особенно важно отметить актуальность работы в MS Excel, как наиболее доступном и простом для понимания программном продукте.

Однако изучение алгоритма автора и внедрение его в работе предприятия показало на некоторые недоработки. О них и пойдет речь в данной статье.

Пропустим вступление об аддитивных и мультипликативных моделях, т.к. оно представляет теоретическую базу, с которой можно ознакомиться в самой статье и начнем с анализа алгоритма прогнозирования объемов продаж. В результате анализа алгоритма, в первой части статьи будет предложен его доработанный вариант.

Вторым разделом статьи будет использование доработанного алгоритма на примере, который предоставил Кошечкин С.А.

1. Определение тренда . Первым шагом в построении модели является выбор линии тренда. Автор утверждает, что выбор полиномиальной линии тренда дает наиболее точную модель, опираясь на коэффициент детерминации, как критерий оценки всей модели в целом. Однако он пропускает тот факт, что точность модели зависит не только от ошибок моделирования тренда, но и от ошибок моделирования сезонных колебаний. Другими словами, модель F=T+S+E (F – значения модели, T – значения линии тренда, S – значения сезонной компоненты, E – величина ошибок) зависит от двух ключевых параметров Т и S, а не только от Т, как утверждает автор. Параметр Е определяет доверительный интервал модели и дает возможность анализировать точность построенной модели.

Выбор наиболее точной линии тренда (Т) с высоким коэффициентом детерминации не является достаточным условием построения оптимальной модели. При росте коэффициента детерминации уменьшается ошибка тренда, но не модели в целом. Таким образом, автор отсекает альтернативные модели, утверждая, что они заранее менее точны, опираясь при этом на данные анализа одного параметра всей модели – тренда (T).

2. Определение величин сезонной компоненты.Необходимо учитывать также ошибки сезонных колебаний (S), которые характеризуются суммой средних величин сезонной компоненты. Чем дальше от 0 значение суммы колебаний сезонной компоненты, тем больше ошибка параметра S. Кстати говоря, автор сообщает о том, что перечень товаров, относящихся к сезонным достаточно велик, но не рассказывает о том, как определить относится ли товар, продаваемый предприятием, к сезонному.

Таким образом, выбирая линию тренда, характеризующую общую тенденцию развития изучаемого явления, необходимо также рассчитывать сезонную компоненту (S) и смотреть на сколько сильно сумма средних значений S отклоняется от 0. Если эта величина близка к 0, то можно утверждать, что продажи действительно имеют сезонный характер и товар, следовательно, можно называть сезонным.

Следующим упущением автора является отсутствие изучения периода сезонных колебаний. С одной стороны – специалисты сами знают: когда начинают расти продажи, а когда падать, но с другой – не у всех товаров сезонные колебания явно выражены. Кроме того, мнение эксперта еще точнее и убедительнее, когда оно подтверждено конкретными данными.

Итак, если мы уже определили, что в модели существует сезонность (сумма значений S близка к 0), то период сезонности рассчитывается как средняя арифметическая между количеством отрицательных и положительных значений сезонной компоненты.

3. Расчет ошибок модели. Изучив поведение сезонной компоненты можно переходить на следующий этап моделирования – расчет ошибок построенной модели. Ошибки рассчитываются по формуле:

при этом вместо значений F подставляются фактические значения объемов продаж.

После нахождения среднеквадратической ошибки модели мы можем делать вывод о точности модели в целом.

4.Построение прогноза. Когда мы определили самую точную модель мы можем перейти на этап прогнозирования, который также описан автором не полностью.

Ведь задача была поставлена в статье «составить прогноз продаж продукции на следующий год по месяцам». А результат, полученный после прогнозирования, характеризуется одним числом. Следовательно, задача, поставленная самим автором, не решена в полном объеме.

Существует также ряд неясностей в ходе дальнейшего прогнозирования:

Почему взяты данные за январь (F_{ф t-1}=2 361), тогда как оба исследуемых периода начинаются с июля месяца.

Как и кем определяется константа сглаживанияа. Ведь экспертом, работающим над данной проблемой, является сам автор. А, следовательно, необходим инструментарий определения данной величины.

Почему не описан инструментарий получения данных доверительного интервала (± 7,8 (руб.)).

Какие «все возможные сценарии прогноза» автор имеет в виду: те которые зависят от константы сглаживания, или те, которые определяются альтернативными моделями.

Таким образом, автором допущены ошибки использования собственного алгоритма. Эти ошибки позволяют сделать вывод о его несовершенстве или о недостаточной конкретизации самого алгоритма. При этом, следует учесть, что основная идея алгоритма, методики и последовательность действий, выбранные автором, абсолютно верны. Следовательно, доработки требует только алгоритм.

С учетом описанных выше недостатков, можно предположить, что алгоритм должен иметь такой вид:

Таблица 1. Алгоритм прогнозирования объемов продаж.

Рассчитываемые показатели

Критерий оценки

Значение к которому стремиться критерий оценки

1. Построение модели F=T+S+E

Определение трендов, для построения альтернативных моделей (T1, T2, T3 …)

Количество

Чем больше, тем правильнее будет выбор

Определение уравнений линий трендов (вид, который принимает T1, T2, T3 …, в зависимости от величин объема продаж)

Коэффициент детерминации

Определение метода расчета сезонной компоненты (в нашем случае это расчет средней арифметической)

Наличие данных

Максимальное количество наблюдаемых периодов (минимум=2)

Определение величин сезонной компоненты (S)

Сумма средних значений колебаний

Определение ошибок модели (E)

СКО (среднеквадратическое отклонение) для каждого периода

Определение точности всей модели

[1- СКО для всей модели]*100%

100,00%

Определение доверительного интервала модели

(F*[1-СКО]; F*[1+СКО])

2. Построение прогноза

Определение прогнозных значений

Фактическое значение будущего периода

Фактическое значение будущего периода (проверка будет осуществлена только по достижении периода)

Определение константы сглаживания

Корректировка прогнозных значений, с использованием экспоненциального сглаживания

Из таблицы видно, что алгоритм не претерпел существенных изменений. Методики, используемые автором в статье, остаются теми же, следовательно, процессуально алгоритм не был усложнен. Однако произведена конкретизация:

разбивка на этапы моделирования и прогнозирования;
детализация каждого из этапов;
определение критериев оценки каждого из этапов;
определение критических значений критериев оценки. Т.е. чем ближе показатель к величине, указанной в последнем столбце – тем вернее будут модель и прогноз.

С учетом проведенных изменений алгоритма попробует использовать его на примере, предоставленном Кошечкиным С.А.

ПРИМЕР.

Исходные данные: объёмы реализации продукции за два сезона. В качестве исходной информации для прогнозирования была использована информация об объёмах сбыта мороженого “Пломбир” одной из фирм в Нижнем Новгороде. Данная статистика характеризуется тем, что значения объёма продаж имеют выраженный сезонный характер с возрастающим трендом. Исходная информация представлена в табл. 1.

Таблица 2. Фактические объёмы реализации продукции