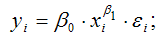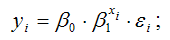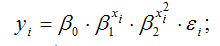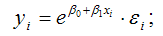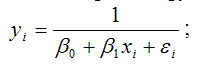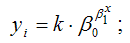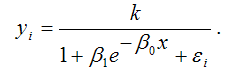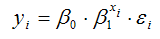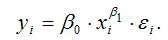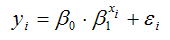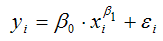Уравнение показательной функции имеет вид эконометрика (3 видео)

Показательное уравнение регрессии

В случае b = e (примерное значение экспоненты e ≈ 2.718281828 ), показательное уравнение регрессии называется экспоненциальным и записывается как y=a·e x .

Здесь b — темп изменения в разах или константа тренда, которая показывает тенденцию ускоренного и все более ускоряющегося возрастания уровней.

Пример . Необходимо изучить зависимость потребительским расходами на моторное масло (у) и располагаемым личным доходом (х). <table x + ε

Составляем систему нормальных уравнений с помощью онлайн-калькулятора Нелинейная регрессия .
a•n + b∑x = ∑y
a∑x + b∑x 2 = ∑y•x

Для наших данных система уравнений имеет вид
21a + 20439.4 b = 32.32
20439.4 a + 20761197.38 b = 31007.03
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = -0.000515, a = 2.04
Уравнение регрессии (эмпирическое уравнение регрессии):
y = e 2.04 *e -0.000515x = 7.69529*0.99948 x
Эмпирические коэффициенты регрессии a и b являются лишь оценками теоретических коэффициентов β_i, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Для расчета параметров регрессии построим расчетную таблицу (табл. 1) <table 2log(y) 2x·log(y)622.91.59388004.412.53989.936581.654329642.721084.82700.41.7490560.162.911194.01740.61.72548488.362.971275.88774.41.72599695.362.971334.11816.21.67666182.442.781361.18853.51.61728462.252.591373.66876.81.55768778.242.391356.99001.538100002.331373.45951.41.61905161.962.591531.221007.91.691015862.412.841699.721004.81.441009623.042.061441.971010.81.441021716.642.061450.581056.21.531115558.442.331611.821105.41.481221909.162.21637.771162.31.551350941.292.391798.731200.71.551441680.492.391858.161209.51.361462890.251.851646.11248.61.281559001.961.641599.371254.41.281573519.361.641606.81284.61.391650197.161.921780.8320439.432.3220761197.3850.131007.03

1. Параметры уравнения регрессии.
Выборочные средние.

Выборочные дисперсии:

Среднеквадратическое отклонение

Содержание

Эконометрика
Тема 4. Множественная регрессия.
Вопросы
1. Нелинейная регрессия. Нелинейные модели и их линеаризация.
Нелинейная регрессия
Модели регрессии, нелинейные по оцениваемым коэффициентам
🎦 Видео

Видео:Показательные уравнения. 11 класс.Скачать

Эконометрика

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ

Кафедра экономико-метематических моделей

Тема 4. Множественная регрессия.

Вопросы

1. Нелинейная регрессия. Нелинейные модели и их линеаризация.

Нелинейная регрессия

При рассмотрении зависимости экономических показателей на основе реальных статистических данных с использованием аппарата теории вероятности и математической статистики можно сделать выводы, что линейные зависимости встречаются не так часто. Линейные зависимости рассматриваются лишь как частный случай для удобства и наглядности рассмотрения протекаемого экономического процесса. Чаще встречаются модели которые отражают экономические процессы в виде нелинейной зависимости.

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций.

Различают два класса нелинейных регрессий:

регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам: регрессии, нелинейные по оцениваемым параметрам.

Нелинейные регрессии по включаемым в нее объясняющим переменным, но линейные по оцениваемым параметрам

Данный класс нелинейных регрессий включает уравнения, в которых зависимая переменная линейно связана с параметрами. Примером могут служить:

полиномы разных степеней

(полином k-й степени)

и равносторонняя гипербола

При оценке параметров регрессий нелинейных по объясняющим переменным используется подход, именуемый «замена переменных». Суть его состоит в замене «нелинейных» объясняющих переменных новыми «линейными» переменными и сведение нелинейной регрессии к линейной регрессии. К новой «преобразованной» регрессии может быть применен обычный метод наименьших квадратов (МНК).

Полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез.

Среди нелинейной полиноминальной регрессии чаще всего используется парабола второй степени; в отдельных случаях — полином третьего порядка. Ограничение в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, менее однородна совокупность по результативному признаку.

Равносторонняя гипербола, для оценки параметров которой используется тот же подход «замены переменных» (1/x заменяют на переменную z) хорошо известна в эконометрике.

Она может быть использована, например, для характеристики связи удельных расходов сырья, материалов и топлива с объемом выпускаемой продукции. Также примером использования равносторонней гиперболы являются кривые Филлипса и Энгеля..

Регрессии нелинейные по оцениваемым параметрам

К данному классу регрессий относятся уравнения, в которых зависимая переменная нелинейно связана с параметрами. Примером таких нелинейных регрессий являются функции:

• степенная — ;

• показательная — ;

• экспоненциальная —

Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду (например, логарифмированием и заменой переменных). Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции и для оценки её параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.

Примером нелинейной по параметрам регрессии внутренне линейной является степенная функция, которая широко используется в эконометрических исследованиях при изучении спроса от цен: , где у — спрашиваемое количество; х — цена;

Данная модель нелинейна относительно оцениваемых параметров, т. к. включает параметры а и b неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду . Заменив переменные и параметры, получим линейную регрессию, оценки параметров которой а и b могут быть найдены МНК.

Широкое использование степенной функции связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %.

Коэффициент эластичности можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру b.

По семи предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (Y, млн. руб.) от объема капиталовложений ( Х, млн. руб. ).

Видео:Показательная функция. 11 класс.Скачать

Модели регрессии, нелинейные по оцениваемым коэффициентам

Нелинейными по оцениваемым параметрам моделями регрессииназываются модели, в которых результативная переменная y_i нелинейно зависит от коэффициентов модели β₀…β_n.

К моделям регрессии, нелинейными по оцениваемым параметрам, относятся:

1) степенная функция:

2) показательная или экспоненциальная функция:

3) логарифмическая парабола:

4) экспоненциальная функция:

5) обратная функция:

7) логистическая функция или кривая Перла-Рида:

Кривыми насыщения называются показательная, логарифмическая и экспоненциальная функции, т. к. будущий прирост результативной переменной зависит от уже достигнутого уровня функции.

Кривые насыщения применяются для характеристики явлений и процессов, величина роста которых является ограниченной величиной (например, в демографии).

Определение. S-образными кривыми называются кривая Гомперца и кривая Перла-Рида. Данные кривые представляют собой кривые насыщения с точкой перегиба.

S-образные кривые применяются для характеристики явлений, включающий в себя два последовательных процесса – ускорения и замедления достигнутого уровня развития. Подобные явления характерны для демографии, страхования и других областей.

Модели регрессии, нелинейные по оцениваемым коэффициентам, делятся на два класса:

1) модели регрессии, которые можно с помощью преобразований привести к линейному виду;

2) модели регрессии, которые невозможно привести к линейному виду.

Рассмотрим первый класс моделей регрессии.

Показательная функция вида

является нелинейной по коэффициенту β₁ и относится к классу моделей регрессии, которые можно с помощью преобразований привести к линейному виду. Данная модель характеризуется тем, что случайная ошибка ε_i мультипликативно связана с факторной переменной хi.

Данную модель можно привести к линейному виду с помощью логарифмирования:

Для более наглядного представления данной модели регрессии воспользуемся методом замен:

В результате произведённых замен получим окончательный вид показательной функции, приведённой к линейной форме:

Таким образом, можно сделать вывод, что рассмотренная показательная функция является внутренне линейной, поэтому оценки неизвестных параметров её линеаризованной формы можно рассчитать с помощью классического метода наименьших квадратов.

Другим примером моделей регрессии первого класса является степенная функция вида:

Данная модель характеризуется тем, что случайная ошибка β_i мультипликативно связана с факторной переменной хi.

Данную модель можно привести к линейному виду с помощью логарифмирования:

Для более наглядного представления данной модели регрессии воспользуемся методом замен:

Таким образом, можно сделать вывод, что рассмотренная степенная функция является внутренне линейной, поэтому оценки неизвестных параметров её линеаризованной формы можно рассчитать с помощью классического метода наименьших квадратов.

Рассмотрим второй класс моделей регрессии, нелинейных по оцениваемым коэффициентам.

Показательная функция вида

относится к классу моделей регрессии, которые невозможно привести к линейной форме путём логарифмирования. Данная модель характеризуется тем, что случайная ошибка β_i аддитивно связана с факторной переменной хi.

Степенная функция вида

относится к классу моделей регрессии, которые невозможно привести к линейной форме путём логарифмирования. Данная модель характеризуется тем, что случайная ошибка εi аддитивно связана с факторной переменной хi.

Таким образом, для оценки неизвестных параметров моделей регрессии, которые нельзя привести к линейному виду, нельзя применять классический метод наименьших квадратов. В этом случае используются итеративные процедуры оценивания (квази-ньютоновский метод, симплекс-метод, метод Хука-Дживса, метод Розенброка и др.).