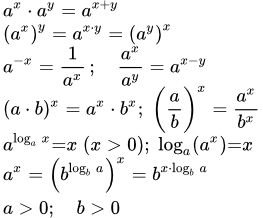Уравнение показательного роста и убывания (2 видео)

Интегрированный урок в 11-м классе по теме: «Дифференциальные уравнения показательного роста и показательного убывания»

Разделы: Математика

Цели урока:

Повысить уровень знаний учащихся по предмету, сделать более понятной важную тему высшей математики, привлекая к уроку учителей биологии и физики.
Выделить разные виды решения задач, расширить кругозор учащихся.
Повысить интерес к предмету, уровень культуры речи, культуры ведения записей.
Учить мыслить, анализировать, приучать к самостоятельности.

Начинает урок учитель математики, объясняя смысл темы: Дифференциальное уравнение – это уравнение, в котором неизвестной является функция от одного неизвестного переменного, причем в это уравнение входят не только сама неизвестная функция, но и ее производные различных порядков.

Термин “дифференциальные уравнения” был предложен Г.Лейбницем. Первые исследования уравнений были проведены в конце XVII века в связи с изучением механики и некоторых геометрических задач.

Дифференциальные уравнения имеют большое прикладное значение, являясь мощным орудием исследования задач естествознания и техники, они широко используются в механике, астрономии, физике, во многих задачах химии, биологии. Это объясняется тем, что весьма часто объективные законы, которым подчиняются те или иные явления (процессы), записываются в форме дифференциальных уравнений, а сами эти уравнения являются средством для количественного выражения этих законов. Например, законы механики Ньютона позволяют механическую задачу описания движения системы материальных точек или твердого тела свести к математической задаче нахождения решений дифференциальных уравнений. Расчет радиотехнических схем и вычисление траектории спутников, исследование устойчивости самолета в полете и выяснение течения химических реакций – все это производится путем изучения и решения дифференциальных уравнений.

Простейшее дифференциальное уравнение имеет вид:

F’(x) = f(x) … (1), где f(x) – данная функция, а F(x) – решение этого уравнения.

Мы будем рассматривать дифференциальное уравнение вида:

Смысл дифференциального уравнения … (2) заключается в том, что скорость изменения функции в точке x пропорциональна значению самой функции в этой точке.

Приведем примеры, в которых величины изменяются по указанному закону.

Объяснение продолжает учитель физики. Она рассматривает задачу 1 о радиоактивном распаде вещества: Если m’(t) скорость радиоактивного распада в момент времени t, то скорость уменьшения массы пропорциональна его количеству.

Значит, решением уравнения … (1) является функцией m’(t) = Сe. С найдем из условия, что в начальный момент времени масса радиоактивного вещества была равна:

m(0) = Сe,

Отсюда, m(t) = m_o · e

Промежуток времени T, через который масса радиоактивного вещества уменьшится в 2 раза называют “периодом полураспада”. Зная Т, можно найти k:

m(T) = m_o ,

m_o · e= m_o,

Логарифмируя по основанию е, получаем

k =

Например, для радия Т 1550 лет. Поэтому, k 0,000447

Следовательно, через 1 млн. лет от начальной массы m_o останется (вычисления проводит учитель математики).

m(10)m_o · e m_o · e0,6 · 10 m_o

Пусть e= y, ln y = – 447, y = 7,37 · 10 = 0,7 · 10

lg y = – 447 lg e = – 447 · 0,4343 = – 194,1321 = – 195 + 0,8679.)

Задача 2. От m_мг радия С через t мин. радиоактивного распада остается n_мг. Найдите период полураспада радия С, т. е. через сколько минут останется 0,5 m_мг радия С.

Дано:

Найти: Т

Решение:

m(t) = m_o · e,

n = m · e,

e =

Далее решение ведет учитель математики:

– kt = ln,

—kt = – ln,

k = .

Зная, что через Т останется 0,5 т_мг радия С, имеем

m(T) = m_o, т.е.

m_oe = m_o,

me = m,

e = ,

– T = – ln2,

– ln T = t(-ln2),

T = =

Ответ: T =

В урок включается учитель биологии. У нее интересный материал о размножении бактерий.

m’(t) = km(t), где k > 0, зависящее от вида бактерий и внешних условий. Решениями этого уравнения являются функции m(t) = C · e. Постоянную C можно найти из условия, что в момент t = 0 масса m_o бактерий известна, тогда m(t) = m_o · e.

Задача 4. Культуре из 100 бактерий представляется возможность размножаться при благоприятных условиях. Через 12 часов число бактерий достигло 500. Сколько бактерий будет через 2 суток после начала опыта?

N (48)Решение:

N(t) = N_oe,

500 = 100 · e,

e = 5,

Значит: N (48) = 100e = 100e = 100 · 626 = 62600

Вычисления проводит учитель математики.

e = y

ln y = 4ln 5 · lg e = 4 · 1,6094 · 0,4343 = 2,7958

Ответ: 62600

В работу включается учитель физики.

Задача 5. Два тела имеют одинаковую температуру – 100 o . Они вынесены на воздух, его температура 0 o . Через 10 мин. температура одного тела стала 80 o , а второго – 64 o . Через сколько минут после начала остывания разность их температур будет равна 25 o .

Содержание

Решение показательных уравнений через возрастание-убывание
Теория
Пример решения показательного уравнения
Показательная функция – свойства, графики, формулы
Определение
Свойства показательной функции
Частные значения
Графики показательной функции
Возрастание, убывание
Обратная функция
Дифференцирование показательной функции
Производная показательной функции
Пример дифференцирования показательной функции
Интеграл
Выражения через комплексные числа
Разложение в ряд
🎥 Видео

Видео:Показательная функция. 11 класс.Скачать

Решение показательных уравнений через возрастание-убывание

Иногда решение показательных уравнений приходится проводить функционально-графическим методом. Одним из направлений этого метода является использование возрастания и убывания функций, отвечающих частям решаемого уравнения. В этой статье мы будем разбираться с решением показательных уравнений через возрастание-убывание. Здесь мы рассмотрим соответствующую теорию и приведем пример решения показательного уравнения через возрастание-убывание.

Видео:Показательные уравнения. 11 класс.Скачать

Теория

Через возрастание-убывание решаются, в основном, показательные уравнения, удовлетворяющие следующим условиям:

для их решения не подходят другие более простые и привычные методы решения показательных уравнений,
область допустимых значений (ОДЗ) для уравнения представляет собой некоторый числовой промежуток,
функции, отвечающие частям уравнения, непрерывны на ОДЗ, при этом очевидно убывание одной из них и возрастание другой, либо есть возможность это доказать,
очевиден корень уравнения, или он каким-либо способом может быть получен, часто подбором.

Например, таким показательным уравнением является .

Выполнение всех перечисленных выше условий гарантируют, что уравнение имеет единственный корень.

Из сказанного вырисовывается метод решения уравнений через возрастание-убывание. Для того, чтобы решить уравнение через возрастание-убывание, в том числе и показательное, надо

Убедиться, что ОДЗ для него есть некоторый числовой промежуток.
Доказать, что функции, отвечающие частям уравнения, непрерывные, и одна из них убывает, а другая – возрастает.
Определить каким-либо способом корень уравнения. Этот корень является единственным.

Вновь обратимся к показательному уравнению . Его ОДЗ есть числовой промежуток x≥−1 . Функции и y=2 −x +5 , отвечающие частям этого уравнения, являются непрерывными на ОДЗ. Возрастание первой из них и убывание второй можно обосновать при помощи свойств возрастающих и убывающих функций. Несложно подобрать корень уравнения, им является число 0 . Из всего сказанного следует, что показательное уравнение имеет единственный корень 0 .

Метод решения уравнений через возрастание убывание распространяется и на уравнения f(x)=C , где f – непрерывная и монотонная (возрастающая или убывающая) функция на ОДЗ для исходного уравнения, C – некоторое число. В качестве примера такого показательного уравнения приведем уравнение . Более того, при помощи этого метода, но с некоторыми корректировками, можно решать уравнения, ОДЗ для которых представляет собой не один числовой промежуток, а объединение нескольких числовых промежутков. Об этом подробно сказано в общей статье решение уравнений через возрастание-убывание. Там же приведено обоснование метода, даны рекомендации по доказательству возрастания-убывания, а также рекомендации по подбору корня уравнения.

Видео:Свойства функции. Промежутки возрастания и убывания функции. 10 класс.Скачать

Пример решения показательного уравнения

Давайте рассмотрим пример решения через возрастание-убывание типичного показательного уравнения . Оно типично в том плане, что удовлетворяет всем без исключения условиям, при которых уравнение решают именно посредством использования возрастания и убывания функций, отвечающих его частям. Действительно. Во-первых, не видно альтернативных методов его решения. Во-вторых, ОДЗ для него есть один числовой промежуток – множество всех действительных чисел. В-третьих, несложно обосновать убывание функции, отвечающей левой части уравнения, а функция, отвечающая правой части, очевидно, возрастающая. Наконец, возможно подобрать корень этого показательного уравнения – им является число 1 . А теперь давайте запишем решение подробно со всеми необходимыми разъяснениями.

Решите показательное уравнение .

Видео:11 класс, 11 урок, Показательная функция, её свойства и графикСкачать

Показательная функция – свойства, графики, формулы

Видео:Промежутки возрастания и убывания функции. 10 класс.Скачать

Определение

Обобщение выполняется следующим образом.
При натуральном x = 1, 2, 3. , показательная функция является произведением x множителей:
.
При этом она обладает свойствами (1.5-8) (см. ниже ⇓), которые следуют из правил умножения чисел. При нулевом и отрицательных значениях целых чисел , показательную функцию определяют по формулам (1.9-10). При дробных значениях x = m/n рациональных чисел, , ее определяют по формуле(1.11). Для действительных , показательную функцию определяют как предел последовательности:
,
где – произвольная последовательность рациональных чисел, сходящаяся к x : .
При таком определении, показательная функция определена для всех , и удовлетворяет свойствам (1.5-8), как и для натуральных x .

Строгая математическая формулировка определения показательной функции и доказательство ее свойств приводится на странице «Определение и доказательство свойств показательной функции».

Видео:ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ 10 класс решение показательных уравненийСкачать

Свойства показательной функции

Показательная функция y = a x , имеет следующие свойства на множестве действительных чисел ( ) :
(1.1) определена и непрерывна, при , для всех ;
(1.2) при a ≠ 1 имеет множество значений ;
(1.3) строго возрастает при , строго убывает при ,
является постоянной при ;
(1.4) при ;
при ;
(1.5) ;
(1.6) ;
(1.7) ;
(1.8) ;
(1.9) ;
(1.10) ;
(1.11) , .

Другие полезные формулы.
.
Формула преобразования к показательной функции с другим основанием степени:

При b = e , получаем выражение показательной функции через экспоненту:

Частные значения

Видео:ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Графики показательной функции

На рисунке представлены графики показательной функции
y ( x ) = a x
для четырех значений основания степени: a = 2 , a = 8 , a = 1/2 и a = 1/8 . Видно, что при a > 1 показательная функция монотонно возрастает. Чем больше основание степени a , тем более сильный рост. При 0 1 показательная функция монотонно убывает. Чем меньше показатель степени a , тем сильнее убывание.

Видео:11 класс, 12 урок, Показательные уравненияСкачать

Возрастание, убывание

Показательная функция, при является строго монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.

y = a x , a > 1	y = a x , 0 1
Область определения	– ∞	– ∞
Область значений	0	0
Монотонность	монотонно возрастает	монотонно убывает
Нули, y = 0	нет	нет
Точки пересечения с осью ординат, x = 0	y = 1	y = 1
+ ∞	0
0	+ ∞

Видео:Алгебра 10 класс (Урок№21 - Показательная функция.)Скачать

Обратная функция

Обратной для показательной функции с основанием степени a является логарифм по основанию a .

Если 0, ; a ne 1)» style=»width:203px;height:20px;vertical-align:-11px;background-position:-0px -492px»> , то
.
Если 0, ; a > 0, a ne 1)» style=»width:286px;height:20px;vertical-align:-11px;background-position:-386px -469px»> , то
.

Видео:✓ Показательное уравнение | ЕГЭ-2017. Задание 12. Математика. Профильный уровень | Борис ТрушинСкачать

Дифференцирование показательной функции

Для дифференцирования показательной функции, ее основание нужно привести к числу e , применить таблицу производных и правило дифференцирования сложной функции.

Для этого нужно использовать свойство логарифмов
и формулу из таблицы производных:
.

Пусть задана показательная функция:
.
Приводим ее к основанию e :

Применим правило дифференцирования сложной функции. Для этого вводим переменную

Тогда

Из таблице производных имеем (заменим переменную x на z ):
.
Поскольку – это постоянная, то производная z по x равна
.
По правилу дифференцирования сложной функции:
.

Производная показательной функции

Пример дифференцирования показательной функции

Найти производную функции
y = 3 5 x

Выразим основание показательной функции через число e .
3 = e ln 3
Тогда
.
Вводим переменную
.
Тогда

Из таблицы производных находим:
.
Поскольку 5ln 3 – это постоянная, то производная z по x равна:
.
По правилу дифференцирования сложной функции имеем:
.

Видео:Как решать такие системы показательных уравненийСкачать

Интеграл

Видео:Показательные уравнения. Практическая часть. 11 класс.Скачать

Выражения через комплексные числа

Рассмотрим функцию комплексного числа z:
f ( z ) = a z
где z = x + iy ; i 2 = – 1 .
Выразим комплексную постоянную a через модуль r и аргумент φ :
a = r e i φ
Тогда

.
Аргумент φ определен не однозначно. В общем виде
φ = φ ₀ + 2 πn ,
где n – целое. Поэтому функция f ( z ) также не однозначна. Часто рассматривают ее главное значение
.

Видео:Показательные уравнения — что это такое и как решатьСкачать