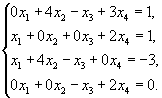Уравнение по высшей математике 1 курс

На этой странице мы собрали простые и сложные примеры из курса высшей математики — от векторов и матриц до дифференциальных уравнений. На каждую тему приведен один решенный пример и даны ссылки на разделы, где собраны другие решения. Фактически, это шпаргалка-каталог типовых задач и решений к ним.

Если вам нужна помощь, узнайте больше о заказе решений по высшей математике.

Далее решенные задачи по темам:

Видео:Курс лекций по высшей математике Производные. Часть 1.Скачать

Высшая математика. Комплексные числа

Задача. Вычислить сумму $(z_1 + z_2)$ и разность $(z_1 — z_2)$ комплексных чисел, заданных в показательной форме, переведя их в алгебраическую форму. Построить операнды и результаты на комплексной плоскости.

Видео:Матан за час. Шпаргалка для первокурсника. Высшая математикаСкачать

Высшая математика. Матрицы

Задача. Найти матрицу, обратную матрице $A$. Сделать проверку.

$$A= begin 1 & 2 & 1 & -1\ 1 & 1 & 0 & 0\ 0 & 2 & 0 & -1\ 1 & 1 & 1 & 0\ end $$

Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Высшая математика. Определители

Задача. Вычислить определитель матрицы $A$

$$A= begin 4 & 5 & 6 & 5 & 11\ 1 & 4 & 2 & 0 & 13\ 1 & 1 & 0 & -1 & 5\ 3 & 2 & 3 & 0 & 7\ 4 & 1 & 2 & 3 & 8\ end $$

Видео:Линейная алгебра: матрицы, определители, метод Крамера. Высшая математикаСкачать

Высшая математика. Системы уравнений

Задача. Исследовать на совместность и решить систему уравнений:

Видео:КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕСкачать

Высшая математика. Векторы

Задача. Написать разложение вектора $X$ по векторам $(a, b, c)$.

Видео:Математика это не ИсламСкачать

Аналитическая геометрия на плоскости

Задача. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Видео:Решаем два варианта Добротина за 2 часаСкачать

Аналитическая геометрия в пространстве

Задача. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.

Видео:Матрицы: начало. Высшая математикаСкачать

Высшая математика. Пределы

Задача. Найти предел функции

Видео:Линейная алгебра, Матрицы: Метод Гаусса. Высшая математикаСкачать

Высшая математика. Производные

Задача. Найти производную от следующей функции

Видео:Высшая математика. Рисую дерево вышматаСкачать

Высшая математика. Исследование функции

Задача. Провести полное исследование функции и построить график.

Видео:Решение системы уравнений методом ГауссаСкачать

Высшая математика. Интегралы

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Высшая математика. Применение интегралов

Задача. Найти длину дуги кривой, заданной параметрическими уравнениями:

$$ x=3(1-cos t)cos t, quad y=3(1-cos t)sin t, quad 0leq t leq pi. $$

Высшая математика. Кратные и криволинейные интегралы

Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Высшая математика. Ряды

Задача. Исследовать сходимость числового ряда

Видео:Матан. Пределы для успешной сдачи зачёта | TutorOnline МатематикаСкачать

Высшая математика. Дифференциальные уравнения

Задача. Найти общее решение линейного дифференциального уравнения первого порядка

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Высшая математика. Теория вероятностей

Задача. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит 8; б) произведение числа очков не превосходит 8; в) произведение числа очков делится на 8.

Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

Высшая математика для 1 курса

Курс лекций для студентов 1 курса по высшей математике любых форм обучения. Я собрала теорию и примеры с решениями к каждой теме, чтобы вы смогли подготовиться к экзамену или освежить память перед контрольной работой!

Высшая математика

Высшая математика — это курс обучения в высших учебных заведениях, включающий высшую алгебру и математический анализ для 1 курса.

Высшая математика включает обычно аналитическую геометрию, элементы высшей и линейной алгебры, дифференциальное и интегральное исчисления, дифференциальные уравнения, теорию множеств, теорию вероятностей и элементы математической статистики.

Часто используется в экономике и технике. Является обязательным предметом в российских высших учебных заведениях, за исключением специальностей, в которых различные разделы математики разнесены по разным дисциплинам.

Линейная алгебра

Линейная алгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения[⇨], системы линейных уравнений[⇨], среди основных инструментов, используемых в линейной алгебре — определители, матрицы[⇨], сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры. Такие объекты как квадратичные и билинейные формы[⇨], тензоры[⇨] и операции как тензорное произведение непосредственно вытекают из изучения линейных пространств, но как таковые относятся к полилинейной алгебре.

Курс лекций на темы:

Векторная алгебра

Векторная алгебра в математике расположена по разделам:

• раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства;
• часть линейной алгебры, занимающаяся векторными пространствами;
• различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).

Курс лекций на темы:

Аналитическая геометрия

Аналитическая геометрия — раздел геометрии, в котором геометрические фигуры и их свойства исследуются средствами алгебры. В основе этого метода лежит так называемый метод координат, впервые применённый Декартом в 1637 году. Каждому геометрическому соотношению этот метод ставит в соответствие некоторое уравнение, связывающее координаты фигуры или тела. Такой метод «алгебраизации» геометрических свойств доказал свою универсальность и плодотворно применяется во многих естественных науках и в технике. В математике аналитическая геометрия является также основой для других разделов геометрии — например, дифференциальной, алгебраической, комбинаторной и вычислительной геометрии.

Курс лекций на темы:

Пределы, непрерывность функций

Понятие предела бесконечной числовой последовательности и предела функции лежит в основе всей теории дифференциального и интегрального исчисления.

Непрерывность функции. Функция f(x) называется непрерывной в точке a, если: 1)эта функция определена в некоторой окрестности точки a; 2)существует предел lim f(x) ; →ax.

Курс лекций на темы:

Производная функции

Производная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.

Курс лекций на темы:

Неопределенный интеграл

Неопределённый интеграл для функции f(x) — это совокупность всех первообразных данной функции.

Курс лекций на темы:

Определенный интеграл

Определённый интеграл — одно из основных понятий математического анализа, один из видов интеграла. Определённый интеграл является числом, равным пределу сумм особого вида (интегральных сумм)[⇨]. Геометрически определённый интеграл выражает площадь «криволинейной трапеции», ограниченной графиком функции[⇨]. В терминах функционального анализа, определённый интеграл — аддитивный монотонный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).

Курс лекций на темы:

Дифференциальное исчисление функций нескольких переменных

Курс лекций на темы:

Обыкновенные дифференциальные уравнения

Курс лекций на темы:

Двойные интегралы

Курс лекций на темы:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Высшая математика 1 курс

Несмотря на то, что зачастую этот предмет в вузах преподается разное количество времени (от 1 семестра для гуманитарных специальностей, и до 3 – для технических), список тем мало отличается. Чаще всего в дисциплине рассматриваются следующие разделы высшей математики: линейная и векторная алгебра, аналитическая геометрия, и линии второго порядка.

Линейная алгебра Матрицы

Изучаются матрицы размерностью n на m следующих видов: квадратные, диагональные, равные, единичные, трапецевидные, и треугольные.

Среди действий, которые возможно над ними выполнять рассматривают следующие:

• Сложение и вычитание матриц, сходных по размерности.
• Умножение их на число, вектор, и на другую матрицу.

Определитель

Изучают понятие определителя, его основные свойства, среди которых следующие:

• Для квадратных матриц А и В действует правило, что определитель произведения чисел А на В равняется определителю произведения В на А. И также равняется определителю А умноженному на определитель В. При этом произведение А на В не равняется произведению В на А.
• Определитель и его транспонируемая версия равны между собой.
• Если определитель содержит ряд из 0, или какие-либо 2 его ряда параллельны, то он равен нулю.
• Если матрица диагональная, то ее определитель есть числа, расположенные по диагонали, умноженные между собой. То же самое правило действует и для треугольных матриц.
• Если у чисел имеется общий множитель, то его можно вынести из определителя.

Изучаются основные правила теоремы Лапласа, связанной с разложением определителя.

Обратная матрица

Изучается понятие невырожденной матрицы. В связи с ним существует следующая схема, по которой вычисляется обратная матрица с положительным определителем:

• Элементы матрицы последовательно заменяются на соответствующие им алгебраические дополнения. В результате этого действия возникает союзная матрица.
• Происходит транспонирование.
• Элементы полученной матрицы нужно разделить на определитель матрицы.

Ранг матрицы

Понятие представляется как самое большое число линейно-зависимых строк матрицы и самый большой порядок, не равняющийся нулю, из миноров первоначальной матрицы.

Ранг матрицы имеет следующие два свойства:

• Он не подвержен изменению после транспонирования, после убирания нулевого ряда, и после совершения преобразований.
• Найти ранг можно по общему числу элементов на главной диагонали, отличающихся от нуля.

Метод Крамера

Используется для нахождения корней уравнений, в которых произведение А и Х равняется В. При этом важно, чтобы определитель А был отличным от нуля.

Если это условие совпадает, то можно воспользоваться следующим алгоритмом:

Находим ak, равное определителю Ак деленному на определитель А. Ак получают из А, подставив в него столбец свободного члена из В.

Метод Гаусса

Для его понятия изучают расширенную матрицу. А также несколько видов систем уравнений: совместные, определенные, равносильные, однородные.

Алгоритм для их решений таков:

• Первым делом находят ранги основной и расширенной.
• Если они отличаются друг от друга, то система является несовместной и на этом решение прекращают.
• Иначе сначала высчитывают базисный минор порядка, затем общее решение системы, и в итоге получают частные решения при подставлении произвольных значений в уравнения.

Векторная алгебра Векторы и операции над ними

Рассматривается основное определение вектора, его свойства, такие как длина и направления. Кроме этого изучают следующие различные векторы: противоположные, нулевые, коллинеарные и компланарные.

Существуют следующие действия над векторами:

• Суммирование;
• Скалярное, векторное и смешанное умножение на другой вектор, а также на другое число.

Рассматривает определения плоскостей и трехмерного пространства.

Прямая на плоскости

Изучают несколько ее основных уравнений: нормальное уравнение, с угловым коэффициентом, через точку и направление, через 2 точки, в отрезках.

Плоскость и прямая в пространстве

Рассматривают уравнения, по которым плоскость задается в пространстве. Такие как: уравнения через точку перпендикулярно к вектору, через 3 точки, нормальное, и в отрезках.

При изучении прямой важно знать каноническое и по 2 точкам, общее, векторное, с направляющими коэффициентами.

Во всех трех случаях рассматривают формулы, по которым можно найти различные углы.

Взаимное расположение плоскостей и прямых

При рассмотрении данного вопроса изучают формулы углов, параллельность, перпендикулярность, принадлежность прямой к плоскости.

Линии второго порядка

В этом разделе рассматриваются определения и свойства нескольких фигур: эллипса, гиперболы и параболы.

В связи с эллипсом изучают его каноническое уравнение, а также определения эксцентриситета и директрис.

При рассмотрении гиперболы, изучают тоже самое, что и у эллипса. Но к этому добавляются понятия фокальных радиусов, а также уравнения асимптот.

При изучении параболы рассматривают, что представляет собой полуфокальный диаметр.

Чаще всего дисциплина высшей математики для первокурсников, заканчивается на изучении вышестоящей темы, но программа предмета может несущественно изменяться в зависимости от вуза.