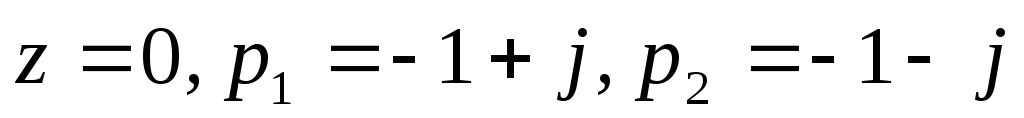Уравнение по точкам в matlab

Видео:Решение произвольных уравнений. Методы вычислений в MATLAB. Часть 1. Урок 61Скачать

Matlab построить график по точкам

Видео:Как в MATLAB Simulink моделировать уравнения (Структурная схема САУ)Скачать

Построение графика по узловым точкам

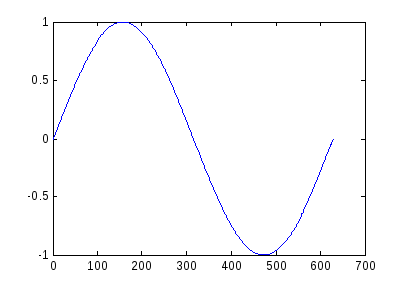
Графики в Matlab, так же как в табличном процессоре, могут быть построены по узловым точкам. Поскольку Matlab — матричная система, совокупность узловых точек у(х) для построения графика задается векторами X и Y одинакового размера.

Графики Matlab строит в отдельных окнах, называемых графическими окнами. С первого взгляда видны отличия графического окна, показанного на рис. 4.5, от командного окна Matlab. В главном меню окна появилась позиция Tools (Инструменты), которая позволяет вывести или скрыть инструментальную панель, видимую в верхней части окна графики на рис. 4.5. Средства этой панели позволяют легко управлять параметрами графиков и наносить на них текстовые комментарии в любом месте.

Рис. 4.5. График, построенный с помощью функции plot

В Matlab для построения графиков функций по узловым точкам в декартовой системе координат служит функция plot. Функция plot имеет несколько синтаксических конструкций:

— plot (X, Y) — строит график функции у(х), координаты точек (х, у) которой берутся из векторов одинакового размера Y и X. Если X или Yматрица, то строится семейство графиков по данным, содержащимся в колонках матрицы;

• — plot( Y) — строит график y(i), где значения у берутся из вектора Y, a i представляет собой индекс соответствующего элемента. Если Yсодержит комплексные элементы, то выполняется команда plot (real (Y), imag( Y)). Во всех других случаях мнимая часть данных игнорируется;
• — plot(X,Y,S) — аналогична команде plot(X,Y), но тип линии графика можно задавать с помощью строковой константы S.

Значениями константы S могут быть символы, приведенные в табл. 4.5.

Построение графиков в matlab командой plot. Она работает с векторами числовых данных. Синтаксис команды представляет собой: plot (X, Y), где X и Y являются векторами одинаковой длины.

Например вот такой график по точкам matlab:

X = [1 2 3]; Y = [4 6 5]; plot (X, Y)

Рис. 2.5. Построение линейных сегментов

• В этом случае мы отделили несколько команд в одной строке с помощью точки
с запятой, вместо запятой. Обратите внимание, что вывод команд,
предшествующих знаку точка с запятой, запрещается.

Команда plot рассматривает вектора X и Y, как перечни координат
последовательных точек на графике, и соединяет точки в виде линейных
сегментов. Таким образом, на Рис. 2.5 показано, как программа MATLAB
соединяет точки с координатами (1, 4), (2, 6) и (3, 5).

Чтобы начертить графики функций matlab например х 2 в интервале от -1 до 2, сначала требуется создать перечень X из значений х, а затем ввести plot (X, Х.^2). (Точка в
данном выражении обязательна, так как Х.^2 представляет собой
поэлементное возведение в квадрат вектора X, но не матричный квадрат.) Нам
необходимо использовать достаточное количество значений х для уверенности в
том, что результирующий график, нарисованный путем соединения точек,
будет выглядеть нормально (плавная, а не ломаная линия). Мы используем
приращение в размере 0.01. Таким образом, чтобы отобразить график
параболы, введите:

X = -1:0.01:2; plot(X, X.^2)

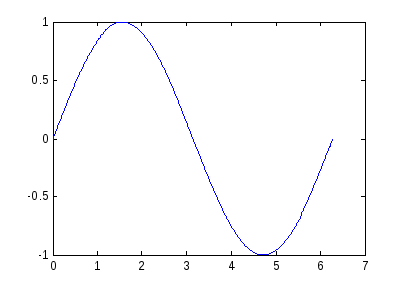
Результат отображен на Рис. 2.6. Обратите внимание, что мы использовали точку
с запятой, чтобы запретить вывод вектора X из 301 элемента.

Рис. 2.6. Построенная парабола

Более подробно графические команды программы MA TLAB рассматриваются в уроке 5.
А пока удовлетворимся демонстрацией построения пары выражений на одном и
том же графике. Надеюсь теперь вы получили подробный ответ на свой вопрос: как строить графики в matlab.

Поэтому из выше всего сказанного можно сделать вывод, что вам необходимо просмотреть много дополнительной информации и альтернатив!

MATLABимеет исключительно мощную систему для построения различных двухмерных и трехмерных графиков, а также их настройки, редактирования и форматирования. Типы и подтипы графиковMATLABочень разнообразны. Список функций двумерной графики можно получить командойhelp graph2d, трехмерной –help graph3d.

Графики выводятся в отдельных графических окнах с помощью команды вида figure(n), гдеn – номер графического окна. На одном графике можно построить несколько кривых, отличающихся цветом и типами линий и точек. Графики могут быть скопированы и вставлены в другие приложения:Word,Excel,PowerPointи др. Для этого используется командаEdit/ Copy Figureокна графики.

Часто используемые команды при построении графиков

plot(t,y) % График непрерывной функции y(t)

plot(x1, y1, x2, y2) % Графики зависимостей y1 от x1 и y2 от x1

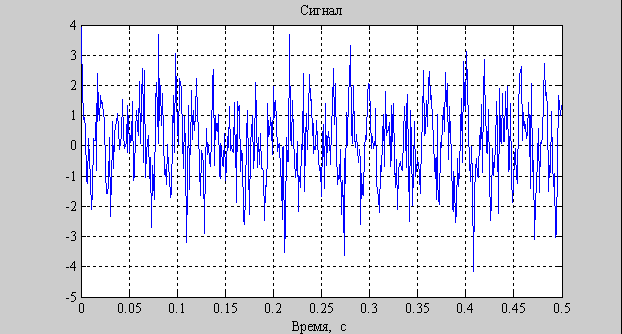
stem(x,y) %График дискретной функции (сигнала)y(x)

stairs(x,y) % График в виде ступенчатой линии

loglog(f,Y) %График с логарифмическими масштабами по x и y

semilogx(f,Y) %Логарифмический масштаб поxи линейный поy

polar(phi,r) % График в полярных координатах

title(‘ название’) % Вывод заголовка графика

xlabel(‘время’) % Метка по осиx

ylabel(‘Напряжение’) % Метка по осиy

legend(‘АЧХ системы‘) % Вывод поясняющей надписи

axis([xmin, xmax, ymin, ymax]) % Установка масштабов по осямxи y

xlim([xmin,xmax]) % Установка масштаба по осиx

ylim([ymin,ymax]) % Установка масштаба по осиy

figure(n) % Устанавливает фигуру (окно)nактивной

subplot(r,c,n) % Разбивает графическое окно наr * cподокон иsubplot(rcn) % устанавливает подокноn в качестве активного.

gridon% к графику добавляется сетка

holdon% позволяет построить несколько графиков в окне

holdoff% отменяетholdonдля текущего графика

text% позволяет разместить текст на графике

zoomon/off% включение / выключение возможности увеличения % фрагментов графика с использованием

% левой и правой кнопок мыши

Построение графика зависимости функции yот индекса массива (номера элемента)x

Построение графика зависимости y(x)

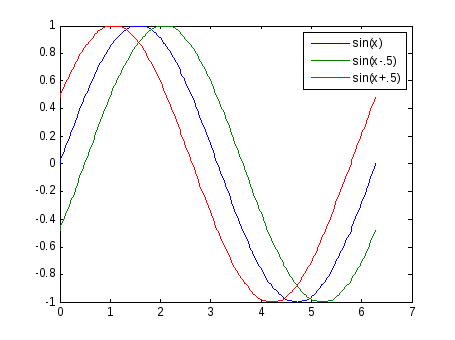
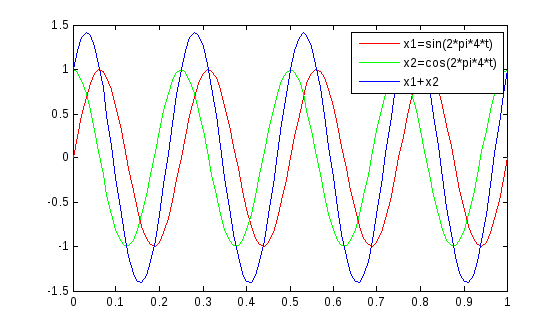
Несколько пар аргументов в функции plot()позволяют построить несколько графиков в одном графическом окне. При этомMATLABдля каждого графика использует отдельный цвет линии.

Цвет, тип линии и обозначение (тип) точек являются аргументами функции plot, соответствующие справочные сведения можно получить с помощью команды вызова справкиhelp plot .

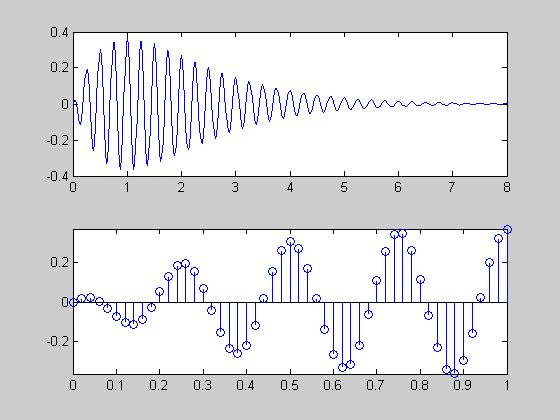
Для разбиения графического окна на подокна служит команда plot(m,n,p)илиplot(mnp),в которойm– число строк,n— число столбцов,p— номер подокна. Пример построения графика функции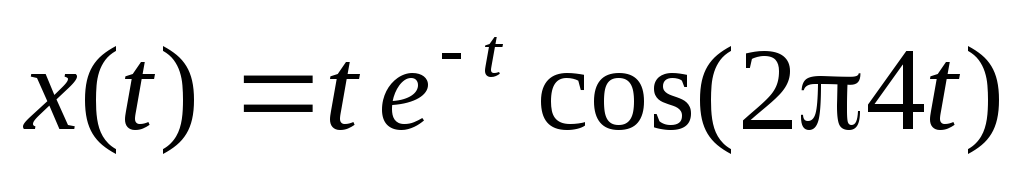в двух подокнах с помощью функцииplot()в одном случае и функцииstem()в другом с разными пределами по оси аргумента (рис. 7):

t=linspace(0, 8, 401); % вычисление 402 точек в интервале [0,8]

axis([0 1 min(x) max(x)] )

Fs=1024; % Частота отсчетов

f1=50; % частота гармоники

N=512; % число отсчетов сигнала

t=0:1/Fs:(N-1)/Fs; % вектор времени

plot(t,x), grid % график сигнала

Для добавления графиков к уже существующим применяют команду hold on

Для отмены действия hold on (освобождения окна графики) используют hold off.

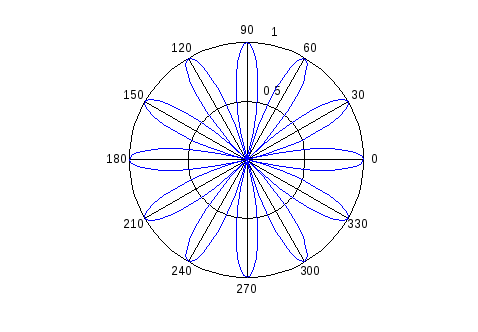
Пример построения графика в полярной системе координат

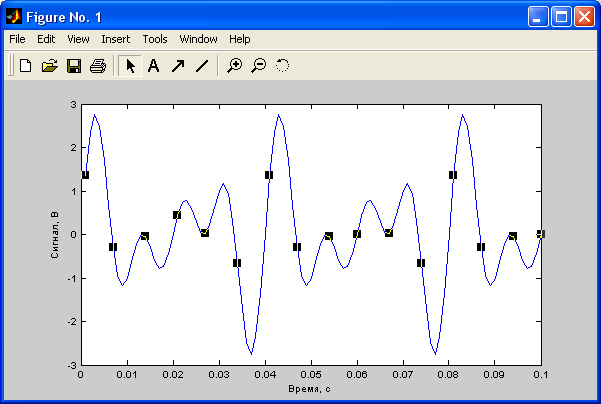
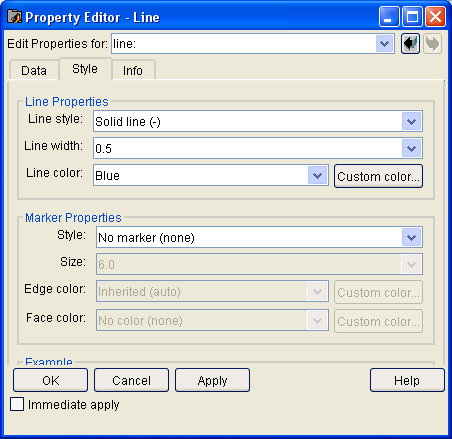
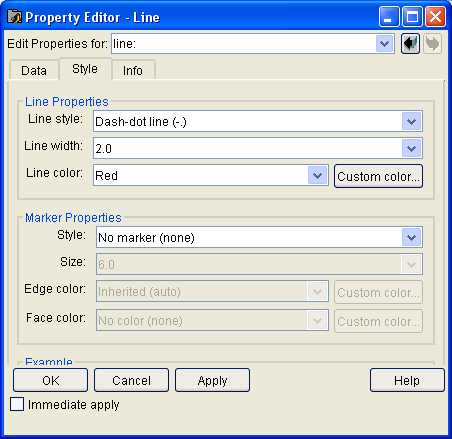
В окне графики MATLABпозволяют выполнять разнообразную настройку графического окна и его объектов с помощью меню или панели инструментов (рис.9).

В окне редактора или с помощью контекстного меню по правой кнопке мыши производятся необходимые установки (цвет, размер, тип, толщина линии и др.) объекта окна графики.

Возможности для подобной интерактивной настройки графики — очень широкие. В первую очередь они обеспечиваются кнопкой Edit Plot инструментальной панели окна.

Трехмерная графика MATLAB– очень развитая и многообразная, сама по себе очень важная часть программы, но в курсе «Сигналы и системы» она используется редко.

Некоторые из команд построения 3D– графиков

>> plot3(…) % строит аксонометрическое изображение 3D-поверхности

>> mesh(…) % строит трехмерные поверхности со специфицированной

Пример построения графика передаточной функции системы второго порядка с передаточной функцией .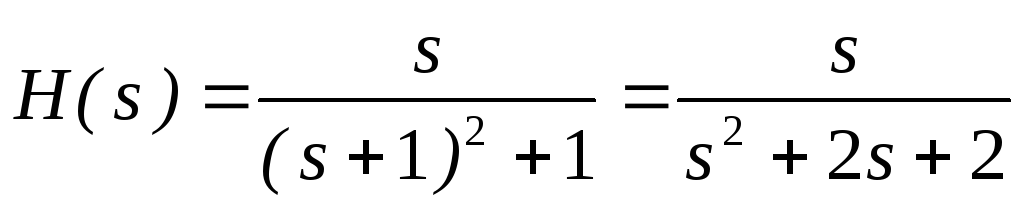

Нули и полюса системы :

Видео:2 - Решениt систем линейных алгебраических уравнений (СЛАУ) с помощью Matlab.Скачать

Как найти уравнение графика, соединяющего точки данных в Matlab?

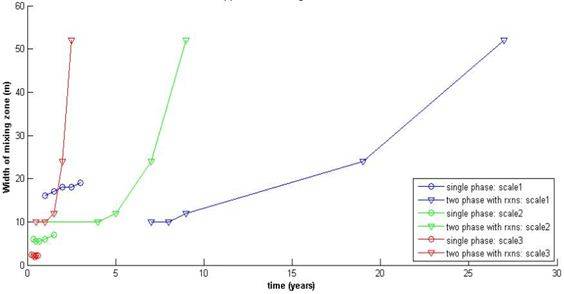
У меня есть различные сюжеты (с hold on ), как показано на следующем рисунке:

Я хотел бы знать, как найти уравнения этих шести кривых в Matlab. Спасибо.

Видео:MATLAB 04 Массивы и матрицыСкачать

5 ответов

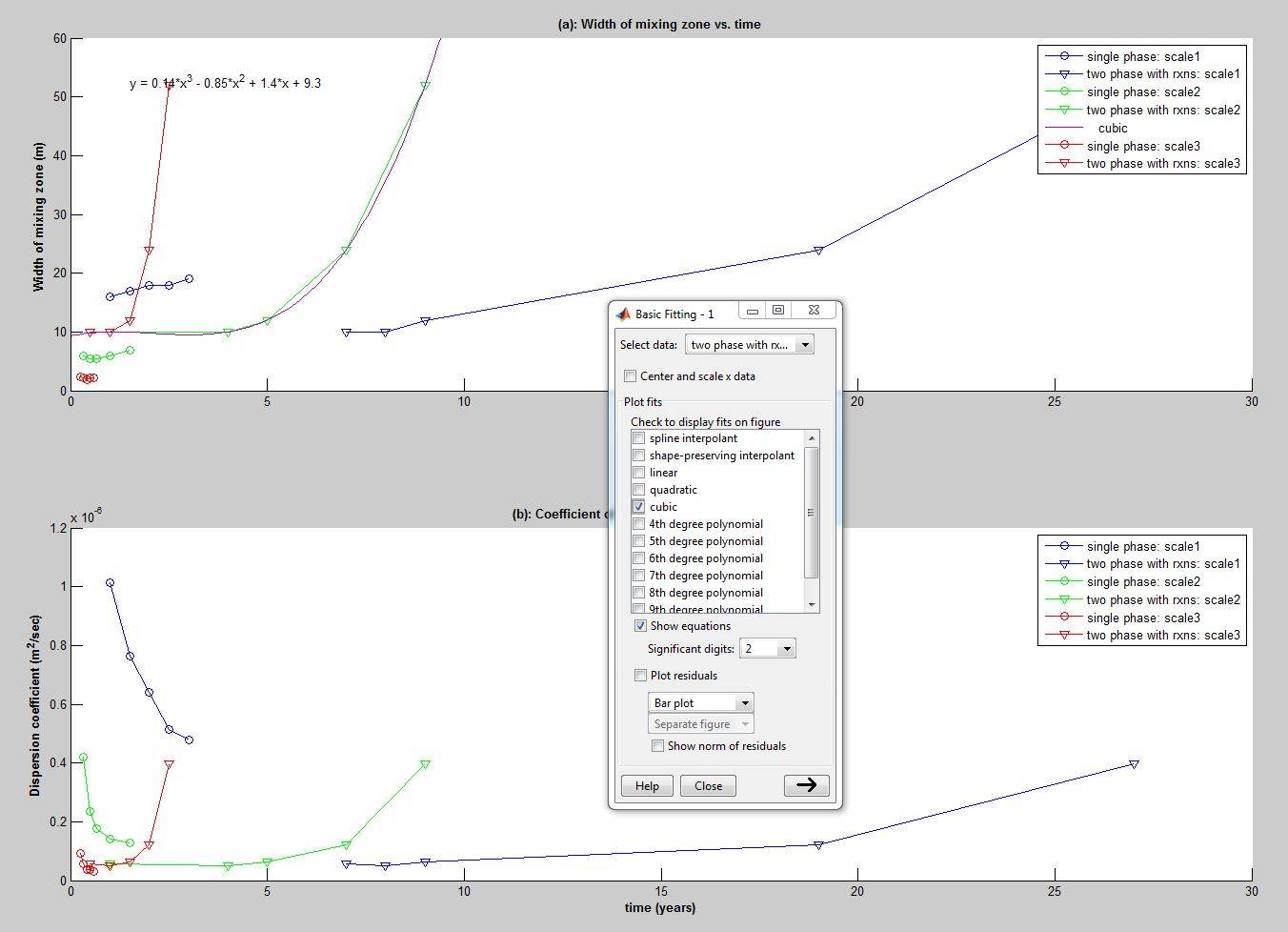
нашел интерактивный инструмент установки в Matlab простой и полезный, хотя несколько ограниченный по объему:

график выше кажется линейной интерполяцией. Учитывая векторы X и Y данных, где X содержит аргументы, а Y-точки функции, вы можете сделать

чтобы получить линейно интерполированное значение f (x). Например, если данные

должно дать вам очень грубое приближение к 1.5^2 . interp1 будет точно соответствовать графику, но вас могут заинтересовать более причудливые операции подгонки кривых, такие как сплайн приближений и т. д.

тут rxns подставка для реакции? В этом случае, ваши кривые, скорее всего, экспоненциальный. Экспоненциальная функция имеет вид: y = a*exp(b * x) . В твоем случае, y — ширина зоны смешивания и x — это время в годах. Теперь, все, что вам нужно сделать, это запустить экспоненциальная регрессия в Matlab найти оптимальные значения параметров a и b , и у вас будут свои уравнения.

совет, хотя может быть лучший ответ, от меня: попробуйте увидеть скорость увеличения кривой. Например, кубический является более репрезентативным, чем квадратичный, если скорость увеличения кажется быстрой и найти полином и вычислить ошибку отклонения. Для нерегулярных кривых, вы можете попробовать сплайн сторона. Я думаю, что в matlab также есть набор инструментов для сплайн-фитинга.

существует способ извлечения информации с помощью текущего дескриптора фигуры (gcf) из вашего графика.

например, вы можете получить ряд, который был нанесен на график:

должна быть другая информация, которую вы можете получить от » findall(gcf. )» методы.

Видео:ТАУ. Matlab/SIMULINK Фазовые портреты нелинейных и линейных диф. уравненийСкачать

Уравнение по точкам в matlab

3 -е занятие по MATLAB

ЛАБОРАТОРНАЯ РАБОТА №3

Трехмерная графика в MATLAB .

Решение обыкновенных дифференциальных уравнений в MATLAB .

1. Элементарная трехмерная (3- D ) графика — функция plot 3.

Функция plot 3 в определенном смысле является аналогом функции plot . С помощью plot 3 формируется построение линии в трехмерном пространстве по заданным трем векторам .

Пример 1.1. Построение трехмерной пространственной спирали.

t =0:0.05:9* pi ; x =2* sin ( t ); y = cos ( t ); % t , x , y — вектора одинакового размера

xlabel( ‘о сь X’ ),ylabel( ‘ось Y’ ),zlabel( ‘ось Z-t’ )

title(‘ Пространственная спираль ‘)

% Сохранить программу в текстовом редакторе MATLAB, например, под именем sp3

% Поменять местами x, y, t в функции plot3

% Сменить начертание и цвет графика

% Добавить пояснение к начертанию в виде легенды — legend( ‘ звездочки ‘ )

%Установить следующий диапазон для t: t=-9*pi:0.05:9*pi;

% Пояснения к графику с помощью функций gtext для 3D-графики не применяются

Пример 1.2. Построение сферы по окружностям.

n=input(‘n=’); % Клавиатурный ввод числа n по запросу в командном окне

t2=(pi/2)*(-n:5:n)’/n ; % транспонированный вектор

E=ones(size(t1)); % матрица единиц размерности вектора t1

% Сохранить программу в текстовом редакторе MATLAB под именем sfera3 .

% Программу выполнить при различных значениях n .

% При n =100 изменить шаг в массивах t1 и t2 : для t1 и t2 одновременно: 3, 1, 10, 25, 50

% Для t1=50, для t2=1; для t1=1, для t2=50.

% Программу sfera3 выполнить без клавиатурного ввода, а для заданного числа n .

% Установить в программе различные цвета изображения сферы.

% Использовать различные коэффициенты для t1 и t2: pi/5, pi/10, pi/50, 2*pi, 5*pi одновременно

% и в сочетании с коэффициентом, равным pi (3.14), при одном из векторов ( t1 или t2).

2. Формирование прямоугольной сетки на плоскости — meshgrid .

% Результатом действия функции meshgrid является формирование «основания» в плоскости XOY для построения над этим основанием пространственной фигуры.

3. Построение пространственных сетчатых фигур — mesh.

Z = 1*x.* exp(-x.^2 — y.^2); % Коэффициент 1 заменить: 2, 5, 10, 20

% Для сравнения применить plot3(x,y,Z),grid вместо mesh(Z) .

R=sqrt(x.^2+y.^2)+0.001; %Коэфф. 0.001 введен для исключения деления на ноль

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Для сравнения применить plot3(x,y,Z),grid

4. Сетчатая поверхность с проекциями линий постоянного уровня — meshс.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

5. Сетчатая поверхность с пьедесталом плоскости отсчета на нулевом уровне— meshz.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

6. Построение пространственных сплошных фигур — surf.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

1. С плошная поверхность с проекциями линий постоянного уровня — surfс.

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

% Коэффициент 1 заменить: 5, 10, 20, 0.5, 0.1

8. Стандартные сферические поверхности — sphere .

8 .1. Сфера единичного радиуса — sphere ;

» sphere % равносильно sphere(20);

8.2 Формирование сферы с произвольным радиусом, например, равным 5;

% Выполнить построения с надписями

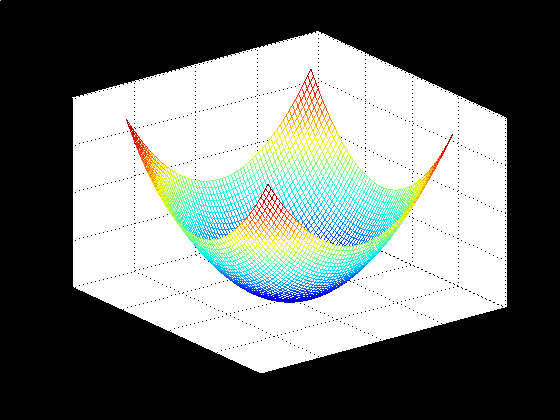
9. Пространственное распределение вероятностей Гаусса — peaks.

peaks; % По умолчанию формируются матрицы размера 49 ´ 49, по которым строится

%поверхность с пометками координат и титульной надписью ‘Peaks’.

peaks, title(‘Gauss’); % Со специальной титульной надписью

peaks(78); % Размерность матриц построения 78 ´ 78

peaks(25); % Размерность матриц построения 25 ´ 25

z=peaks; surf(z); % Построение поверхности Гаусса по заданной 49 ´ 49 матрице z.

% Сравнить с поверхностью на основе функции mesh(z)

% Сравнить с функцией mesh(z)

z=3*peaks(78); surf(z), title(‘Gauss’) % С множителем по оси Z .

% Применить множители: 4, 10, 33, 50

Пример 9.3. Цветовые массивные уровни на плоскости от распределения Гаусса.

[X,Y,Z]=peaks; pcolor(7*X,12*Y,20*Z),title(‘Цвет’) % С расширенной %областью определения на плоскости XOY — множители 7 и 12 и с изменением по Z — коэф-

Пример 9.4. Распределение Гаусса с задаваемой областью определения на плоскости XOY.

% Функция pcolor позволяет наблюдать обл а сть определения в плоскости XOY

% Изменить шаг по x и y : 0.2, 0.1, 0.5

% Изменить границы по x и y одновременно и порознь :(-7:0.2:3),(-7:0.2:1),(-7:0.2:-1),(-7:0.2:-3)

Пример 9.5. Линии уровня трехмерной поверхности — contour.

% Линии уровня без учета масштаба плоскости XOY:

contour(peaks),grid,title(‘ Линии уровня ‘) % 10 линий уровня по умолчанию

contour(peaks,4),grid,title(‘ Линии уровня ‘) % 4 линии уровня

contour(peaks,10),grid,title(‘ Линии уровня ‘) % 10 лини q уровня

contour(peaks,15),grid,title(‘ Линии уровня ‘) % 15 лини q уровня

contour(peaks,25),grid,title(‘ Линии уровня ‘) % 25 лини q уровня

% Применить функцию contour для стандартной сферической поверхности sphere с различным числом линий уровня.

Пример 9.6. Линии уровня с учетом масштаба плоскости XOY (два примера):

Пример 9.7. Линии уровня с учетом масштаба плоскости XOY и заданным числом (три примера):

Пример 9.7. Линии уровня с цветовой окраской плоскости XOY — contourF.

contourF(peaks),title(‘Цвет линий уровня’)

Пример 9.8. «Пространственные» линии уровня — contour3.

contour3(peaks,25),title(’25 л иний уровня в пространстве ‘)

Пример 9.9. Обзор поверхности из заданной точки пространства — view.

peaks,view(10,45); % Число 10 — азимут обзора, 45 — угол обзора (все в градусах)

[X,Y]=meshgrid(-7:0.3:7,-5:0.3:5);Z=peaks(X,Y);surf(Z), view( — 10,45)

% Задать различные параметры функции view и выполнить построение различных поверхностей.

10. Пострение поверхностей относительно полярной системы координат.

Z=peaks(x1,y1);surf(x1,y1,Z),title(‘ Полярная плоскость ‘)

% С изменением точки обзора

Z=peaks(x1,y1);surf(x1,y1,Z),title(‘ Полярная плоскость ‘),view(-12,45)

11. Построение цилиндрических поверхностей — cylinder.

cylinder % Построение цилиндра без параметров, по умолчанию

cylinder(40) % Построение цилиндра с заданным размером плоскости XOY

cylinder(40,60) % Цилиндр с заданным размером плоскости XOY и числом образующих %граней — 60

% Построение совокупности цилиндрообразующих поверхностей

[x,y,z]=cylinder([5 0],160); surf(x,y,z) % Конус по заданному вектору [5,0]

[x,y,z]=cylinder([5 0 5],160); surf(x,y,z) % 2 к онуса

[x,y,z]=cylinder([5 0],3); surf(x,y,z) % Пирамида

[x,y,z]=cylinder([5 0 5],3); surf(x,y,z) % 2 пиирамиды

[x,y,z]=cylinder([5 12 12],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 5],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 12 5],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 5 12 5 12],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 12 5 18],100); surf(x,y,z)

[x,y,z]=cylinder([5 12 12 5 5 18 18],100); surf(x,y,z)

% Построение совокупности цилиндрообразующих поверхностей с масштабированием

[x,y,z]=cylinder([5 12 12 5 5 18 18],100); surf(x,y,20*z)

plot(x,20*z),grid % Масштаб плоскости XOZ

plot(7*x,y),grid % Масштаб плоскости XOY

plot(7*x,13*y),grid % Масштаб плоскости XOY

Решение обыкновенных дифференциальных уравнений в MATLAB.

Для решения обыкновенных дифференциальных уравнений (ODE) могут быть применены численные методы, которые в MATLAB реализованы в специальных функциях-решателях: ode45, ode23, ode113 .

Общий порядок программирования:

1) Создается М-функция с описанием правых частей дифференциальных уравнений;

2) Создается М-сценарий с выбранным решателем;

Пример 1. Решить следующую систему обыкновенных дифференциальных уравнений с заданными начальными условиями:

% Программа решения примера 1

% Создаем М-функцию под именем dif31.m

% Создаем М-сценарий под именем ddd45_31.m

% Сценарий решения с помощью ode45

T=[0 15]; % Интервал интегрирования

x0=[10;5]; % Начальные условия

[t,x]=ode45(‘dif31’,T,x0); %t, x — выходные переменные решателя ode45

plot(t,x),grid,title(‘ Пример 3.1 ‘),legend(‘X1′,’X2’)

% Изменить начальные условия:

% Изменить интервал интегрирования: от 0 до 20, от 0 до 7.

% Вывести графические результаты с различным начертанием координат

% Прменить решатели ode23, ode113 . Сравнить результаты покоординатно, для чего вывести результаты решения и свести их в таблицу, например, в WORD .

Пример 2. Решить следующую систему линейных дифференциальных уравнений с заданными начальными условиями:

% Создаем М-функцию с именем dif32.m

function f=dif32(t,x); % t, x — входные переменные для М-функции

%Создаем М-сценарий под именем ddd45_32

% Сценарий решения примера 2

x0=[0;0;0]; % x0 — вектор начальных условий

% Изменить интервал интегрирования

% Изменить начальные условия

% Вывести графические результаты с различным начертанием координат

% Использовать решатели ode23, ode113 .

Пример 3. Уравнение Ван-дер-Поля.

Для решения дифференциального уравнения 2-го порядка сначала приведем его к системе дифференциальных уравнений 1-го порядка:

где

% Создаем М-функцию под именем van33.m

%Создаем М-сценарий под именем ddd45_33

plot(t,X),grid,title(‘ Ур-е Ван-дер-Поля ‘ ), legend(‘X1′,’X2’)

% Изменить интервал интегрирования

% Изменить начальные условия ( только все нулевые не должны быть)

% Изменить множитель в уравнении (вместо 2)

% Вывести графические результаты с различным начертанием координат

% Использовать решатели ode23, ode113 .

Пример 4. Интегрирование дифференциальных уравнений с выводом результатов в заданн ом диапазоне точек независимого переменного. Видоизменим пример 2 в сценарии задания интервала интегрирования.

% Сценарий решения примера 4

T=[0:1:6,7:2:18]; % от 0 до 6 шаг 1, от 7 до 18 шаг 2

Пример 5. Интегрирование дифференциальных уравнений с выводом результатов в заданных точках независимого переменного. Видоизменим пример 2 в сценарии задания интервала интегрирования.

% Сценарий решения примера 5

T=[0 0.5 1 1.5 3 4 8]; 7 точек переменного t

Задание к примерам 1-5: произвести графический вывод координат каждой в отдельности

Пример 6. Интегрирование систем линейных дифференциальных уравнений в матричном виде, т.е.

(6.1)

где — вектор переменных состояния размера n ´ 1, — вектор входного воздействия размера rx1, — матрицы чисел размера n ´ n, n ´ r, соответственно .

% Матрицы и берем из примера 2

% Создаем М-функцию под именем syst36.m

A=[-3,0,0;1,-2,0;0,4,-1]; % Матрица А размера 3 ´ 3

B=[10 0 0;0 0 0;0 0 0]; % Матрица B размера 3 ´ 3

u=[1;1;1]; % Входное воздействие размера 3 ´ 1

ds36=A*x+B*u; % Описание правой части матричного дифференциального уравнения (6.1)

% Создаем М-сценарий под именем ddd45_36

% Сценарий решения примера 3.6

plot(t,x),grid,title(‘ Система ур-й 3-го порядка ‘),

Задание к примеру 6:

% Решить систему с двумя воздействиями, с одним воздействием

% Вывести графические результаты с различным начертанием координат

% Вывести графические результаты с по отдельным координатам

% Создать программу решения системы дифференциальных уравнений 4-го порядка

% Использовать решатели ode23, ode113 .

Решение обыкновенных дифференциальных уравнений

с заданной точностью и с параметрами.

Решатели дифференциальных уравнений по умолчанию производят численное интегрирование с относительной погрешностью и вектором абсолютной погрешности со значением по всем компонентам вектора.

1. Установление заданной относительной погрешности RelTol — ODESET( odeset) .

С помощью установления относительной погрешности RelTol контролируется количество «правильных» цифр в решении дифференциального уравнения в соответствии с общей записью , где показатель степени P есть число контролируемых цифр в решении.

Пример1. Уравнение Ван-дер-Поля с заданной относительной погрешностью.

С помощью функции ODESET задаются опции решателя дифуравнений с помощью соответствующих строковых символов, которых всего может быть 18. Перечень строковых символов функции ODESET можно просмотреть из командной строки, набрав в ней ODESET

% Сформируем М-функцию для описания правых частей дифференциальных уравнений

% Сохрани ть под именем van33

% Создадим М-сценарий решения на основе ode23 и с относительной погрешностью, равной

% d1= 0.1 и d2=0.0001

% М-сценарий сохранить под именем ret71.

% Формат записи функции odeset включает строковый служебный символ RelTol и задаваемую %величину относительной погрешности (0.1 для d1 и 0.2 для d2).

% d1 и d2 подставляются в соответствующие решатели ( ode23).

Задание к примеру 1:

— выполнить с ode45, ode113;

— изменить коэффициент в М-функции van33 : 0.3, 2.3;

— изменить для d1 относительную погрешность: 1, 0.5, 0.1, 0.01, 0.001, 0.0001 (для ode23).

Пример 2. Анализ нелинейной тест-системы с задаваемой относительной погрешностью вычислений в решателях MATLAB.

где — постоянные действительные числа.

2.1. Проинтегрируем тест-систему с коэффициентами и с относительной погрешностью, равной 0.1, 0.01, 0.001, 0.4, 0.3, 0.2

% Создадим М-функцию под именем dif21

% Создадим М-сценарий под именем syst21

% Введем относительную погрешность 0.1

% В сценарии применим функцию odeset

% Проанализировать тест-систему по 2-й и 3-й координатам.

% Для графического вывода результатов по 2-й координате следует ввести plot в виде

%% Для графического вывода результатов по 3-й координате следует ввести plot в виде

% Проанализировать тест-систему с относительной погрешностью, равной 0.01, 0.4, 0.3, 0.2

% Проанализировать тест-систему с помощью решателей ode45, ode113 , сравнить результаты.

2. Задание абсолютной погрешности — AbsTol .

Абсолютная погрешность AbsTol контролирует разницу между ожидаемым решением и его действительным значением. AbsTol начинает проявляться, когда компонента (координата) решения становится неожидаемо большой. Влияние AbsTol зависит также от интервала и масштаба интегрирования. По умолчанию решатели дифференциальных уравнений Matlab устанавливают величину абсолютной погрешности, равную .

Пример3. Уравнение Ван-дер-Поля с заданной абсолютной погрешностью — ‘AbsTol’ .

% Используем имеющую М-функцию описания уравнения Ван-дер-Поля — van33

% Создадим М-сценарий ( присвоить имя) с задаваемой абсолютной погрешностью по всем координатам и по %одной из возможных

a1=odeset(‘AbsTol’,0.5); % Скаляр 0.1 по всем координатам

% Задание избирательной абсолютной погрешности осуществляется с помощью вектора в виде :

% По первой координате погрешность равна 0.5, по 2-й — 0.000001

% В целом сценарий (присвоить имя) должен иметь вид

% Поскольку система уравнений Ван-дер-Поля имеет взаимозависимые координаты, то интегрирование осуществляется практически с наименьшей погрешностью, т.е. с 0.000001

Задание к примеру 3.

— Применить скаляр абсолютной погрешности: 0.3, 0.1, 0.01.

— Вывести график по 2-й координате.

3. Интегрирование дифференциальных уравнений с параметрами.

Пример 4. Проинтегрировать однородную систему нелинейных дифференциальных уравнений с четырьмя параметрами k1, k2, k3, a:

при следующих начальных условиях:

Целью является анализ решений при различных параметрах, входящих в систему.

% Создадим М-функцию под именем dif44 с ключевым словом flag

switch flag % Начало процедуры описания правых частей дифуравнений

case » % Состояние flag с опциями по умолчанию

end % Окончание описания правых частей дифуравнений с опциями по умолчанию

% Создадим М-сценарий под именем syst44 для решателя ode23 c опциями по умолчанию

% и введения параметров

x0=[0;1;-1]; % Вектор начальных условий

tt=[0,25]; % Интервал интегрирования

k1=input(‘k1=’)%2.333; % Можно также k1=2.333;

k2=input(‘k2=’)%-0.7789; % Можно также k2=-0.7789;

k3=input(‘k3=’)%-0.7888; % Можно также k3=-0.7888;

a=input(‘a=’)%-0.1; % Можно также a=-0.1;

plot(t,x),grid,title(‘ Система с параметрами ‘), legend( ‘x1’ , ‘x2’ , ‘x3’ )

% В записи функции ode23 символ [ ] указывает на опции ( RelTol, AbsTol и др.), принятые по %умолчанию

Задание к примеру 4.

— Изменить параметр k1: 2, 1, 0.5, 0.2; ( остальные исходные) ;

— Изменить параметр k2: -0.111, -0.333,-0.555,0.7789 ( остальные исходные) ;

— Изменить параметр k3: -1.333, -0.333, -0.666, 0.7888 ( остальные исходные) ;

— Изменить параметр a: -1, 1, 0, 0.5 ( остальные исходные) ;

Произвести интегрирование системы при:

Пример 5. Интегрирование систем с циклическим изменением параметра.

% Используем М-функцию dif55

% Видоизменим М-сценарий syst66 так, чтобы программно изменялся какой-либо параметр (например, k3) и происходило наложение графиков решения по заданной координате (например, по ). Новый М-сценарий будет с именем syst77.

if i==-0.51 % Двойное равенство соответствует логической истине

plot(t,x(:,2),’r’),title(‘ Система с циклическим параметром ‘ )

k3=i; % Без точки с запятой (;) выводятся значения k3

Задание к примеру 5.

— Расширить диапазон изменения параметра k3;

— Написать программу с изменением параметра k2 ;

— Написать программу с графическим выводом всех координат системы при k3=0.51 и только координаты при остальных значениях параметра k3 .

🎥 Видео

Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать

MATLAB 07 Интерактивное построение графиковСкачать

Обучение в MATLAB и Simulink: от уравнения к фундаментальным принципамСкачать

1 - Решение систем нелинейных уравнений в MatlabСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

MatLab. Решение дифференциального уравнения.Скачать

ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать

Самый короткий тест на интеллект Задача Массачусетского профессораСкачать

Работа в MATLAB. МКР. Задача КошиСкачать

Математика это не ИсламСкачать

Нативная разработка VS кроссплатформенная разработка | Что выбрать?Скачать

MATLAB 03 Написание программСкачать

Решение системы уравнений Колмогорова в МатлабеСкачать

Символьные и численные расчеты в MATLABСкачать