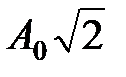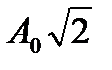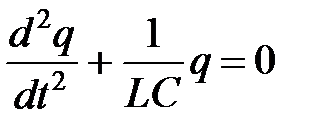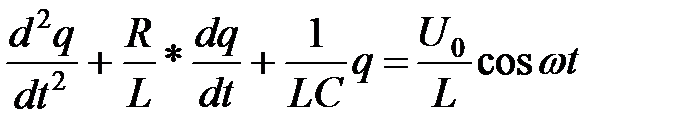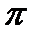Уравнение плоской волны распространяющейся вдоль оси ох имеет вид период равен (6 видео)

Уравнение плоской волны распространяющейся вдоль оси ох имеет вид период равен

отстоящие друг от друга на расстоянии λ, колеблются одинаковым образом.

Уравнение плоской волны

Найдем вид функции . в случае плоской волны, предполагая, что колебания носят гармонический характер.

Пусть колебание точек, лежащих в плоскости x = 0, имеет вид (при начальной фазе ф = 0)

Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время τ = х/v. Следовательно, колебания частиц в плоскости x будут отставать по времени на τ от колебаний частиц в плоскости x = 0, т. е.

— это уравнение плоской волны (рис. 2.4.3). Таким образом, . есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания A = const. Это будет, если энергия волны не поглощается средой.

Такой же вид уравнение (2.4.5) будет иметь, если колебания распространяются вдоль оси y или z.

В общем виде уравнение плоской волны записывается так:

Выражения (2.4.5) и (2.4.6) есть уравнения бегущей волны. Уравнение волны можно записать и в другом виде.

Введем волновое число k = 2π/λ, или в векторной форме

где k — волновой вектор; n — нормаль к волновой поверхности.

Так как λ = vT , то k = 2π/vT = 2πν/v = ω/v. Отсюда v = ω/k.

Тогда уравнение плоской волны запишется так:

Содержание

Колебания и волны
Плоская волна
Определение и основные понятия плоской волны
Уравнение плоской волны
📺 Видео

Видео:Получение уравнения плоской бегущей волны.Скачать

Колебания и волны

Уравнение движения пружинного маятника 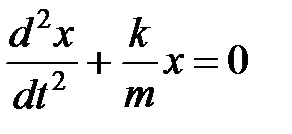является дифференциальным уравнением .

свободных незатухающих колебаний

Уравнение движения пружинного маятника 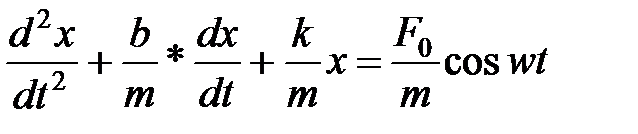является дифференциальным уравнением .

При сложении двух гармонических колебаний одного направления с одинаковыми периодами и равными амплитудами результирующее колебание имеет такую же амплитуду, что и складываемые колебания. При этом разность фаз исходных колебаний равна .

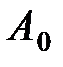
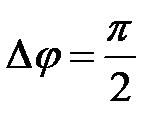
Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами . При разности фаз амплитуда результирующего колебания равна .

Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной .

Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами A_0. При разности фаз амплитуда результирующего колебания равна .

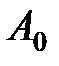
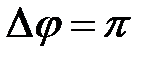
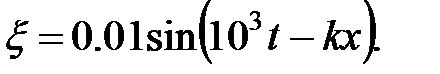
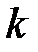
Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ со скоростью 500 м/с, имеет вид Волновое число (в м -1 ) равно .

Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 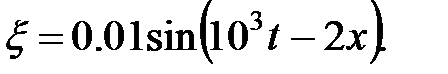Длина волны (в м) равна .

3,14

Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 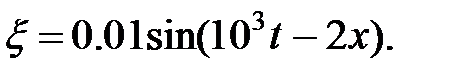Период (в мс) равен .

6,28

Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 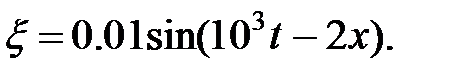Тогда скорость распространения волны (в м/с) равна .

500

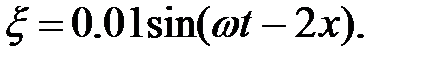
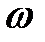
Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ со скоростью 500 м/с, имеет вид Циклическая частота (в с -1 ) равна .

1000

Свободные незатухающие колебания заряда конденсатора в колебательном контуре описываются уравнением.

Вынужденные колебания заряда конденсатора в колебательном контуре описываются уравнением .

Уравнение движения пружинного маятника 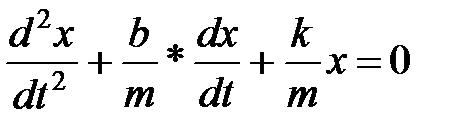Является дифференциальным уравнением .

свободных затухающих колебаний

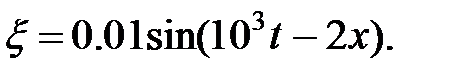
500

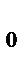
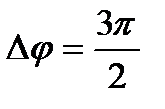
Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами А . При разности фаз амплитуда результирующего колебания равна .

Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет минимальную амплитуду при разности фаз, равной .

Если увеличить в 2 раза объемную плотность энергии и при этом увеличить в 2 раза скорость распространения упругих волн, то плотность потока энергии .

увеличится в 4 раза

На рисунках изображены зависимости от времени координаты и скорости материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний точки равна .

На рисунках изображены зависимости от времени координаты и ускорения материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний точки равна .

Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет минимальную амплитуду при разности фаз, равной .

Сейсмическая упругая волна, падающая со скоростью 5,6 км/с под углом 45° на границу раздела между двумя слоями земной коры с различными свойствами, испытывает преломление, причем угол преломления равен 30°. Во второй среде волна будет распространяться со скоростью .

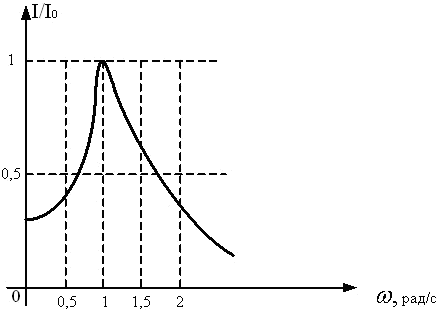
На рисунке представлена зависимость относительной амплитуды колебаний силы тока в катушке индуктивностью1 мГн, включенной в идеальный колебательный контур. Емкость конденсатора этого контура равна .

На рисунках изображены зависимости от времени скорости и ускорения материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний точки равна .

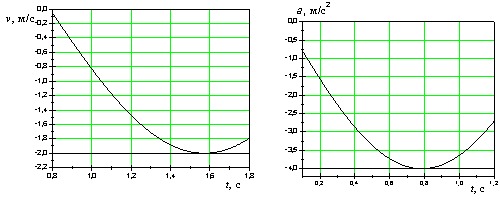Уравнение плоской волны распространяющейся вдоль оси ох имеет вид период равен

2 с -1

Сейсмическая упругая волна, падающая под углом 45° на границу раздела между двумя слоями земной коры с различными свойствами, испытывает преломление, причем угол преломления равен 30°. Во второй среде волна распространяется со скоростью 4,0 км/с. В первой среде скорость волны была равна .

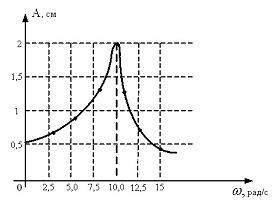
На рисунке представлена зависимость амплитуды колебаний груза на пружине с жесткостью k=10 Н/м от частоты внешней силы. Масса колеблющегося груза равна .

Если увеличить в 2 раза объемную плотность энергии и при этом уменьшить в 2 раза скорость распространения упругих волн, то плотность потока энергии .

Видео:10й класс; Физика; "Уравнение плоской волны"Скачать

Плоская волна

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Определение и основные понятия плоской волны

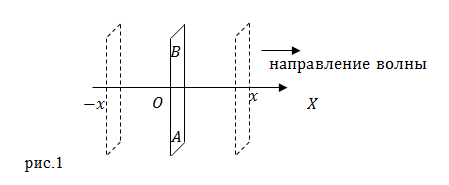
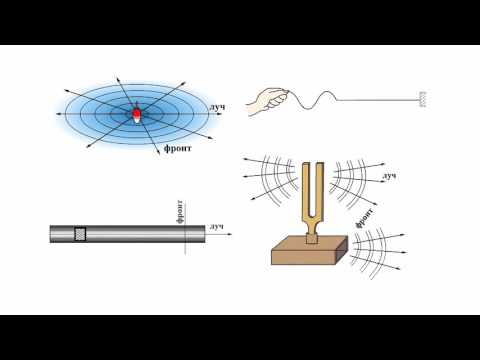
Пусть источником волн в бесконечной упругой среде является бесконечно большая пластина. Она совершает колебания вдоль оси X, плоскость пластины перпендикулярна оси X (рис.1).

Пластина совершает гармонические колебания. Введем следующие обозначения: $s_0$ — смещение точек пластины AB и примыкающих к ней частиц среды от положения равновесия; $A_0$ — амплитуда колебаний пластины; $varphi $ — фаза колебаний; $omega $ — циклическая частота колебаний. Уравнение колебаний пластины имеет вид:

В таком случае в среде распространяется гармоническая волна такой же частоты. Если среда является однородной и изотропной, то колебания всех частиц вещества на одинаковых расстояниях от пластины идентичны (совпадают амплитуды и начальные фазы колебаний). То есть волновые поверхности имеют вид параллельных плоскостей, которые перпендикулярны оси X (направлению волны). Данные волны называют плоскими.

Волны, волновые поверхности которых представляют собой плоскости, называют плоскими.

Видео:Физика 11 класс (Урок№2 - Механические волны.)Скачать

Уравнение плоской волны

Колебания в точках среды, находящихся на расстоянии $x$ от плоскости AB отстают по фазе от колебаний источника на величину $kx$:

при отсутствии рассеяния энергии волны в веществе $A$=$A_0$. $k=frac $- волновое число.

Для точек пространства находящихся правее плоскости AB $x>0$, для точек находящихся левее этой плоскости $x Пример 1

Задание: Плоская гармоническая волна распространяется по прямой, которая совпадает с осью X, в положительном направлении оси. Среда энергию не поглощает. Скорость распространения волны равна $v$. Амплитуда волны $A.$ Две точки, которые находятся на расстояниях $x_1 и x_2$ от источника волны совершают колебания с разностью фаз $Delta varphi =frac$. Какова длина волны? Запишите уравнение волны.

Решение: Запишем уравнение плоской волны:

Фазы колебаний двух точек в этой волне равны:

[_1=omega t-kx_1+varphi ;; _2=omega t-kx_2+varphi left(1.3right).]

Найдем их разность:

[Delta varphi =omega t-kx_2+varphi -left(omega t-kx_1+varphi right)=kleft(x_2-x_1right)=fracleft(x_2-x_1right)left(1.4right).]

Выразим длину волны ($lambda $) из (1.4):

Для написания уравнения волны через известные из условий задачи величины используем формулу:

Можем записать уравнение волны:

Задание: В однородном упругом веществе имеется плоская стоячая волна вида: $s=A$. Нарисуйте графики зависимости $sleft(xright)$ при $t=0$ и $t=frac$, где $T$ — период колебаний.