| Уравнения плоской и сферической волн |   |
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид: Уравнение волны можно записать и в другом виде. Введем волновое число
где Так как
Уравнение сферической волны В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна wt (т.е.
где А равна амплитуде на расстоянии от источника равном единице. Уравнение (5.2.7) неприменимо для малых r, т.к. при Содержание
Видео:10й класс; Физика; "Уравнение плоской волны"Скачать  Уравнение плоской волны как найти периодотстоящие друг от друга на расстоянии λ, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции . в случае плоской волны, предполагая, что колебания носят гармонический характер. Пусть колебание точек, лежащих в плоскости x = 0, имеет вид (при начальной фазе ф = 0) Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время τ = х/v. Следовательно, колебания частиц в плоскости x будут отставать по времени на τ от колебаний частиц в плоскости x = 0, т. е. — это уравнение плоской волны (рис. 2.4.3). Таким образом, . есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания A = const. Это будет, если энергия волны не поглощается средой. Такой же вид уравнение (2.4.5) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так: Выражения (2.4.5) и (2.4.6) есть уравнения бегущей волны. Уравнение волны можно записать и в другом виде. Введем волновое число k = 2π/λ, или в векторной форме где k — волновой вектор; n — нормаль к волновой поверхности. Так как λ = vT , то k = 2π/vT = 2πν/v = ω/v. Отсюда v = ω/k. Тогда уравнение плоской волны запишется так: Видео:Получение уравнения плоской бегущей волны.Скачать  Волновое движение в физике — формулы и определение с примерамиСодержание: Волновое движение: Процесс распространения колебаний в упругой среде называют механической волной. Для механических волн нужна среда, обладающая способностью запасать кинетическую и потенциальную энергию, она должна обладать инертными и упругими свойствами. Различают поперечные и продольные волны. Продольные волны могут распространяться в любых средах: твердых, жидких и газообразных; поперечные – только в твердых средах. Как в поперечных, так и в продольных волнах переноса вещества в направлении распространения волны не происходит. Волны переносят энергию колебаний. Изучив страницу, вы сможете:
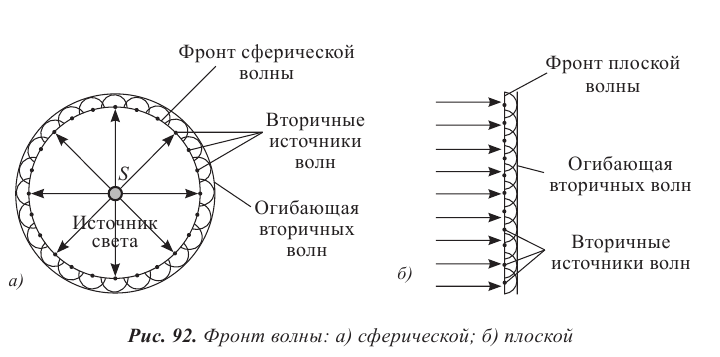
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать  Уравнение бегущей волныКолебательное движение тела в упругой среде является источником механической волны. Волну, переносящую энергию, называют бегущей волной. В однородной среде скорость распространения волны остается величиной постоянной. Смещение y (x, t) от положения равновесия частиц среды при распространении волны зависит от координаты x на оси 0х, вдоль которой распространяется волна, и от времени t по закону: где Введем волновое число Смещение точек упругой среды в волне, бегущей в противоположном направлении выбранной оси 0х, можно определить по формуле: Вспомните! Основные характеристики волн. Волны, созданные источником, совершающим гармонические колебания, характеризуются амплитудой колебания частиц среды A, частотой Длиной волны Видео:Амплитуда, период, частота и длина волны периодических волнСкачать  Физический смысл волнового числаЗапишем формулу (2), выразив циклическую частоту через период Бегущая волна обладает двойной периодичностью – во времени и в пространстве. Временной период равен периоду колебаний T частиц среды, пространственный период равен длине волны Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать  Фронт волны и волновая поверхностьВолна за время, равное периоду колебаний, достигает точек пространства, расположенных от источника на расстоянии длины волны. Совокупность этих точек представляет собой фронт волны, который отделяет колеблющиеся точки среды от точек, не вовлеченных в колебательное движение. Фронт волны от точечного источника представляет собой сферу, от плоской пластины – плоскость, от струны – форму цилиндра (рис. 79–81). Фронт волны – это геометрическое место точек пространства, до которых дошли колебания в данный момент времени t. Направление распространения волны указывает луч, который перпендикулярен фронту волны. В волне можно рассмотреть множество поверхностей, все точки которых совершают колебания синфазно, их называют волновыми поверхностями. При множестве волновых поверхностей, фронт волны только один. Геометрическое место точек пространства, которые совершают колебания в одинаковой фазе в данный момент времени, называют волновой поверхностью. Видео:Волны. Основные понятия. Решение задач.Задача 1Скачать  Стоячие волныУравнение стоячей волны При отражении от более плотной среды волна, изменив свое направление на обратное, меняет фазу на Получим уравнение стоячей волны путем сложения уравнений бегущих волн: Заменив волновое число его значением Координаты точек пучностей и узлов определяются из условий наибольшего и наименьшего значений амплитуды. При При Расстояния между двумя соседними пучностями или двумя соседними узлами равны: В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не переносится в другие части струны. В каждом таком отрезке происходит дважды за период превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Отсутствие переноса энергии является отличительной особенностью стоячей волны. Пример: Уравнение бегущей волны, изображенной на рисунке (рис. 85): А. Получите уравнение стоячей волны как сумму падающей и отраженной волн. В. Полученное выражение запишите, заменив волновое число и циклическую частоту через длину волны и период. С. Определите положение узлов и пучностей. Дано: Решение: А. Уравнение стоячей волны определятся сложением уравнений бегущих волн: В. С. При С. Расстояние от узлов определим из условия Ответ: Интерференция волнЕсли в некоторой среде несколько источников возбуждают механические волны, то они распространяются независимо друг от друга. Все точки среды принимают участие в колебаниях, вызванных каждой волной в отдельности. Наложение волн, в результате которой появляется устойчивая картина чередующихся максимумов и минимумов колебаний частиц среды, называют интерференцией. Интерферировать могут только волны, имеющие одинаковую частоту и постоянный сдвиг фаз. Такие волны называют когерентными, их создают источники, колеблющиеся с одинаковой частотой и постоянным значением сдвига фаз. Интерференция волн – взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга. Интерференция бывает стационарной и нестационарной. Стационарную интерференционную картину могут давать только когерентные волны: например, две сферические волны на поверхности воды, распространяющиеся от двух когерентных точечных источников (рис. 87). Запомните! Волны называют когерентными, если их источники совершают колебания одной частоты с постоянным сдвигом фаз. Условие максимума и минимума при интерференции двух волнАмплитуда колебаний при наложении волн определяется в соответствии с принципом суперпозиции (рис. 88). Если в некоторой точке среды накладываются гребни когерентных волн, то происходит усиление колебаний, амплитуда принимает значение, равное сумме амплитуд. Если накладывается гребень одной волны с впадиной другой волны, то при равенстве амплитуд отдельно взятых волн данная точка пространства не совершает колебания. Если амплитуды отличаются, то колебания в этой точке совершаются с амплитудой равной разности амплитуд распространяющихся волн. Для определения результата интерференции волн, распространяющихся от двух источников А и В, находящихся на расстоянии где так как волна за период пробегает расстояние равное длине волны Минимум колебаний в рассматриваемой точке среды наблюдается в том случае, если от двух когерентных источников распространяются волны со сдвигом фаз, равным нечетному числу p, а разность хода лучей кратна нечетному числу полуволн. В этом случае колебания происходят в противофазе (рис. 90). Возьмите на заметку: Интерференция волн приводит к перераспределению энергии колебаний между частицами среды. Это не противоречит закону сохранения энергии, так как в среднем, для большой области пространства, энергия результирующей волны равна сумме энергий интерферирующих волн. Распространение волн. Принцип Гюйгенса – ФренеляНа основе принципа Х. Гюйгенса: каждая точка среды, до которой дошло возмущение, является источником вторичных волн, невозможно объяснить, почему источники вторичных волн создают фронт только по направлению распространения волны. Для объяснения явлений распространения волны французский физик О. Френель в 1815 г. дополнил принцип Х. Гюйгенса представлениями о когерентности и интерференции вторичных волн. При наложении вторичных когерентных волн происходит интерференция, в результате которой амплитуда колебаний в различных точках пространства становится разной: по направлению распространения волны усиливается, в обратном направлении – уменьшается. Огибающая фронты вторичных волн является фронтом результирующей волны (рис. 92). Дифракция механических волнВторичные волны, созданные точками среды, которые находятся на краю отверстия или препятствия, искривляются и волна огибает препятствие (рис. 93 а–г). Дифракция – это явление огибания волнами препятствий. Все волны способны огибать препятствия, если длина волны соизмерима с размерами препятствия. Дифракция становится заметной, если размеры препятствия меньше длины волны. Физика в нашей жизни: Струнные музыкальные инструменты Интересно знать! Адырна (рис. 96 а) – один из древнейших казахских струнных инструментов. В его форме отобразилась воинственность кочевников-казахов: он напоминает изогнутый лук воина. Деревянный корпус инструмента легкий, так как он пустотелый. Струны изготавливают из кусков специально выделанной кожи или сплетенных из верблюжьей шерсти нитей. Музыкант играет, перебирая струны. Их в инструменте 13. Жетыген (рис. 96 б) – семиструнный музыкальный инструмент. Он имеет прямоугольную форму, изготовлен из дерева, струны – из конского волоса. Легенда о жетыгене раскрывает причину использования именно семи струн. Старик, потерявший семерых сыновей, вылил свое горе, исполняя кюи о них. Вспоминая каждого из сыновей, он натягивал новую струну на музыкальном инструменте. Условие возникновения стоячей волны в струнеСтоячая волна в струне возникает только в том случае, если длина Набору значений В отличие от груза на пружине или маятника, у которых имеется единственная собственная частота, струна обладает бесконечным числом собственных резонансных частот. На рисунке 96 в изображены несколько типов стоячих волн в струне. Стоячие волны различных типов могут одновременно присутствовать в колебаниях струны. Визуализация звуковых волнСуществует несколько способов демонстрации стоячей волны, один из них – фигуры Хладни (рис. 97). Немецкий физик Эрнст Хладни получал узор, посыпая пластинку песком и проводя по краю смычком. Движения смычка заставляли пластинку колебаться на некоторой резонансной частоте. Песок скапливался и лежал неподвижно в узлах, а на участках, где отраженная волна усиливала бегущую, песок смещался. Интересно знать! В Шотландии есть рослинская капелла св. Матвея, на одной из арок которой есть 213 резных каменных кубов, с вырезанным на них геометрическим рисунком. Многие исследователи пытались понять, что зашифровано в рисунках на кубах. Отставной генерал ВВС Томас Митчел со своим сыном, пианистом Стюартом Митчелом предложили оригинальный способ расшифровки послания. Они сопоставили геометрические рисунки с фигурами Хладни и пришли к выводу, что на кубах записаны ноты. Собрав ноты воедино и творчески обработав их, они представили миру произведение «Рослинский Мотет». Итоги: Глоссарий Волновая поверхность – геометрическое место точек, имеющих одинаковую фазу колебаний. Дифракция – явление огибания волнами препятствий. Интерференция волн – взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга. Когерентные волны – волны, имеющие одинаковую частоту и постоянный сдвиг фаз. Механическая волна – процесс распространения колебаний в упругой среде. Фронт волны – геометрическое место точек пространства, до которых дошли колебания в данный момент времени t. Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать  Распространение колебаний в упругих средах. Продольные и поперечные волныОпыт показывает, что колебания, возбужденные в какой-либо точке упругой среды, с течением времени передаются в ее другие точки. В качестве примера достаточно вспомнить, что измерение пульса осуществляется на запястье, хотя сердце расположено внутри грудной клетки. Такие явления связаны с распространением механических волн. Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой. Механические волны не могут распространяться в вакууме. Подчеркнем, что при распространении волны отсутствует перенос вещества, т. е. частицы колеблются вблизи положений равновесия. Среднее смещение частиц за большой промежуток времени равно нулю. Волновой фронт — это воображаемая поверхность, до которой дошло волновое возмущение в данный момент времени. Линия, проведенная перпендикулярно волновому фронту в направлении распространения волны, называется лучом. Луч указывает направление распространения волны. Основными характеристиками волны являются (рис. 208):
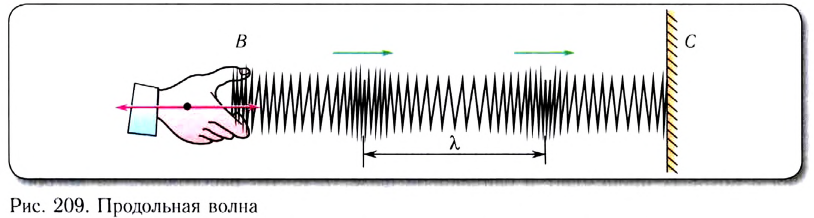
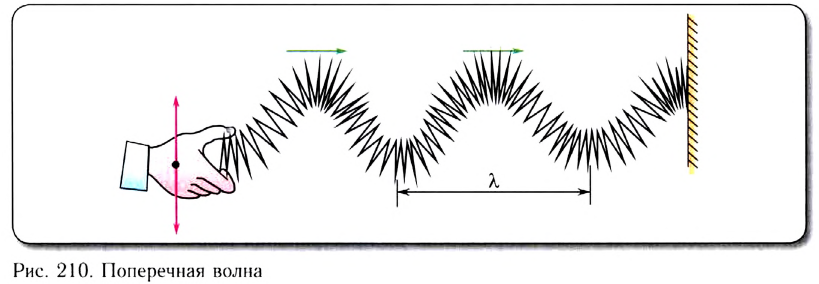
Рассмотрим колебания источника волны, происходящие с циклической частотой В некоторую точку среды колебания придут не мгновенно, а через промежуток времени, определяемый скоростью волны и расстоянием от источника до точки наблюдения. Если скорость волны в данной среде равна v, то зависимость от времени t координаты (смещения) х колеблющейся точки, находящейся на расстоянии r от источника, описывается функцией Выражение х(t, r) называется уравнением плоской волны, распространяющейся (бегущей) вдоль направления радиус-вектора Бегущую волну можно наблюдать, проведя следующий опыт: если один конец резинового шнура, лежащего на гладком горизонтальном столе, закрепить и, слегка натянув шнур рукой, привести его второй конец в колебательное движение в направлении, перпендикулярном шнуру, то по нему побежит волна, описываемая уравнением плоской волны. Рассмотрим классификацию бегущих волн по направлению колебаний частиц среды, в которой они распространяются. Волна называется продольной, если колебания частиц среды происходят вдоль направления распространения волн. Продольную волну легко получить с помощью длинной пружины, которая лежит на гладкой горизонтальной поверхности и один конец ее закреплен. Легким ударом по свободному концу В пружины мы вызовем появление волны (рис. 209). При этом каждый виток пружины будет колебаться вдоль направления распространения волны ВС. Примерами продольных волн являются звуковые волны в воздухе и жидкости. Волна называется поперечной, если частицы среды колеблются в плоскости, перпендикулярной направлению распространения волны. С помощью длинной пружины можно продемонстрировать распространение поперечных волн, если совершать колебания незакрепленного конца перпендикулярно пружине (рис. 210). Поперечные волны вызывают звучание струн музыкальных инструментов при их возбуждении. Продольные колебания симметричны относительно линии распространения ВС, и их действие на любой регистрирующий прибор не изменяется, если прибор будет поворачиваться вокруг направления распространения. Действие поперечных волн на регистрирующий прибор зависит от того, в какой плоскости, проходящей через линию распространения, происходит колебание. Эта особенность поперечных волн носит название поляризации. Если колебания происходят в одной плоскости, то волну называют плоско или линейно поляризованной. Если конец вектора колебаний, например вектора смещения, скорости, напряженности электрического поля, описывает эллипс или окружность, то волну называют эллиптически или циркулярно-поляризованной. До сих пор мы рассматривали волны, распространяющиеся в какой-либо среде. Волны, которые распространяются на границе раздела двух сред, называются поверхностными волнами. Примером данного типа волн служат волны на поверхности воды. Звуковые волны. Скорость звука. УльтразвукЗвуком называются колебания среды, воспринимаемые органами слуха. Звуковая волна — упругая продольная волна, представляющая собой зоны сжатия и разрежения упругой среды (например, воздуха), распространяющиеся в пространстве с течением времени. Таким образом, в процессе распространения звуковой волны меняются такие характеристики среды, как давление и плотность. Звуковые волны классифицируются по частоте следующим образом:
Многие животные могут воспринимать ультразвуковые частоты. Например, собаки могут слышать звуки до 50 000 Гц, а летучие мыши — до 100 000 Гц. Инфразвук, распространяясь в воде на сотни километров, помогает китам и многим другим морским животным ориентироваться в толще воды. Одной из важнейших характеристик звуковых волн является спектр. Спектром называется набор различных частот, образующих данный звуковой сигнал. Спектр может быть сплошным или дискретным. В сплошном спектре присутствуют волны, частоты которых заполняют весь заданный спектральный диапазон. дискретном спектре — конечное число волн с определенными частотами и амплитудами, которые образуют рассматриваемый сигнал. По типу спектра звуки разделяются на шумы и музыкальные тона. Шум — совокупность множества разнообразных кратковременных звуков (хруст, шелест, шорох, стук и т.п.) — представляет собой наложение большого числа колебаний с близкими амплитудами, но различными частотами (имеет сплошной спектр). Музыкальный тон создается периодическими колебаниями звучащего тела (камертон, струна) и представляет собой гармоническое колебание одной частоты. На основе музыкальных тонов создана музыкальная азбука — ноты (до, ре, ми, фа, соль, ля, си), которые позволяют воспроизводить одну и ту же мелодию па различных музыкальных инструментах. Музыкальный звук (созвучие) — результат наложения нескольких одновременно звучащих музыкальных тонов, из которых можно выделить основной тон, соответствующий наименьшей частоте. Основной тон называется также первой гармоникой. Все остальные тоны называются обертонами. Обертоны называются гармоническими, если частоты обертонов кратны частоте основного тона. Таким образом, музыкальный звук имеет дискретный спектр. Любой звук, помимо частоты, характеризуется интенсивностью. Интенсивность I — это энергия Другими словами, интенсивность любой волны — мощность, переносимая волной через единичную площадку, расположенную перпендикулярно к направлению распространения волны. Единицей интенсивности в СИ является ватт на метр в квадрате С возрастом порог слышимости человека возрастает. Интенсивность звуковых волн, при которой возникает ощущение боли, называют порогом болевого ощущения или болевым порогом. Интенсивность звука, улавливаемого ухом человека, лежит в широких пределах: от Реактивный самолет может создать звук интенсивностью Уровни интенсивности звука L определяют обычно, используя шкалу, единицей которой является бел (Б) или, что гораздо чаще, децибел (дБ) (одна десятая бела). 1 Б самый слабый звук, который воспринимает наше ухо. Единица названа в честь изобретателя телефона А. Г. Белла. Измерение уровня интенсивности в децибелах проще, поэтому принято в физике и технике. Уровень интенсивности L любого звука в децибелах вычисляется через интенсивность звука по формуле
Так, поезд метро создает уровень интенсивности звука 100 дБ, мощные усилители — 120 дБ, а реактивный самолет — 150 дБ. Тем, кто при работе подвергается воздействию шума свыше 100 дБ, следует пользоваться наушниками. Физическим характеристикам звука соответствуют определенные (субъективные) характеристики, связанные с восприятием его конкретным человеком. Это связано с тем, что восприятие звука — процесс не только физический, но и физиологический. Действительно, человеческое ухо воспринимает звуковые колебания определенных частот и интенсивностей (это объективные, не зависящие от человека характеристики звука) по-разному, в зависимости от «характеристик приемника» (здесь влияют субъективные индивидуальные черты каждого человека). Основными физиологическими характеристиками звука являются громкость, высота и тембр. Громкость (степень слышимости звука) определяется как интенсивностью звука (амплитудой колебаний в звуковой волне), так и различной чувствительностью человеческого уха на разных частотах, т. е. его способностью улавливать звуки различных частот. Наибольшей чувствительностью человеческое ухо обладает в диапазоне частот от 1000 Гц до При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи Сайт пишется, поддерживается и управляется коллективом преподавателей Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC. Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг. 💡 ВидеоВыполнялка 53.Гармонические колебания.Скачать  4.3 Плоские электромагнитные волны в идеальных диэлектрических средахСкачать 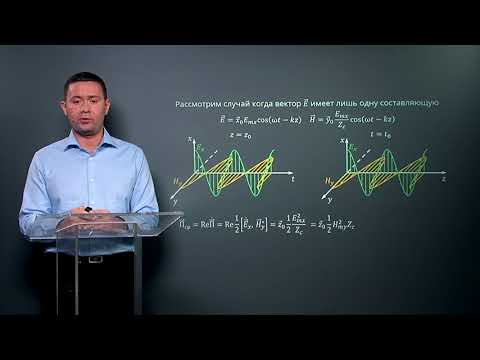 6 ключевых признаков того, что ваш прорыв близокСкачать  Урок 95 (осн). Механические волны. ЗвукСкачать  4.2 Решение волновых уравнений Гельмгольца в виде плоских бегущих волнСкачать  Урок 370. Механические волны. Математическое описание бегущей волныСкачать  КОЛЕБАНИЯ физика 9 класс решение задачСкачать  Урок 92 (осн). Колебательное движение. МаятникиСкачать  Длина волны Связь длины волны со скоростью ее распространения и периодом Уравнение волны converСкачать  Механические модели волн. 1.Скачать  74. Упругие волныСкачать  Урок 94 (осн). Задачи на колебательное движениеСкачать  Урок 327. Гармонические колебанияСкачать  |

 .
. . Пусть колебание точек, лежащих в плоскости
. Пусть колебание точек, лежащих в плоскости  , имеет вид (при начальной фазе
, имеет вид (при начальной фазе  )
)

 .
. ,
, . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой. , или
, или  .
. .
. , или в векторной форме:
, или в векторной форме: ,
, – волновой вектор,
– волновой вектор,  – нормаль к волновой поверхности.
– нормаль к волновой поверхности. , то
, то  . Отсюда
. Отсюда  . Тогда уравнение плоской волны запишется так:
. Тогда уравнение плоской волны запишется так: .
. ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу  . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону  . Следовательно, уравнение сферической волны:
. Следовательно, уравнение сферической волны: , или
, или  ,
, , амплитуда стремится к бесконечности. То, что амплитуда колебаний
, амплитуда стремится к бесконечности. То, что амплитуда колебаний  , следует из рассмотрения энергии, переносимой волной.
, следует из рассмотрения энергии, переносимой волной.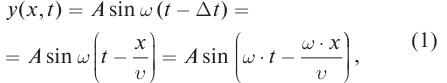
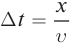
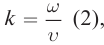 тогда уравнение бегущей волны примет вид
тогда уравнение бегущей волны примет вид 

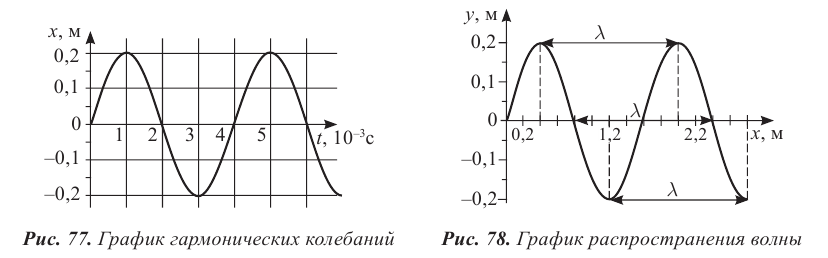
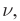 длиной волны
длиной волны 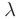 и скоростью распространения
и скоростью распространения 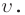
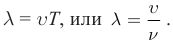 В однородных средах скорость распространения волны величина постоянная.
В однородных средах скорость распространения волны величина постоянная.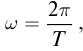 с учетом определения длины волны
с учетом определения длины волны 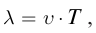 получим:
получим: 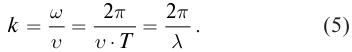
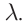 Волновое число
Волновое число 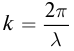 является пространственным аналогом циклической частоты
является пространственным аналогом циклической частоты 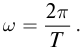
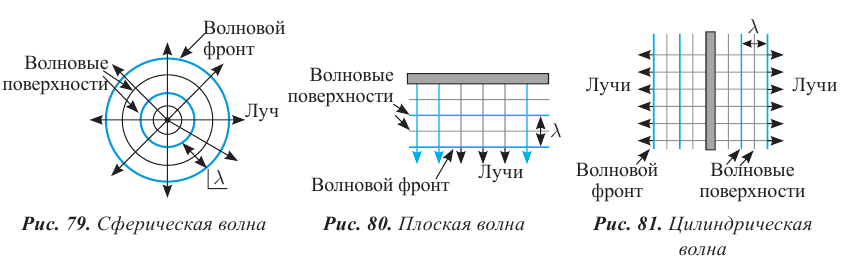
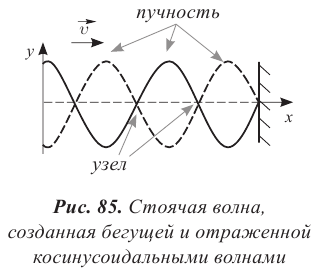
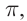 то есть на противоположную. В результате сложения падающей и отраженной волн образуется стоячая волна. Она имеет вид, представленный на рисунке 83. В стоячей волне существуют неподвижные точки, которые называются узлами. Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями.
то есть на противоположную. В результате сложения падающей и отраженной волн образуется стоячая волна. Она имеет вид, представленный на рисунке 83. В стоячей волне существуют неподвижные точки, которые называются узлами. Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями.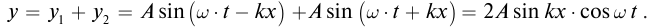
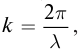 запишем уравнение стоячей волны в виде:
запишем уравнение стоячей волны в виде: 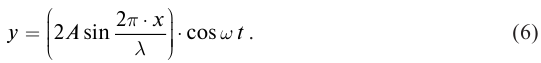
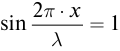 образуется пучность с амплитудой равной 2 А (рис. 84). Расстояния от источника стоячей волны до пучностей равны:
образуется пучность с амплитудой равной 2 А (рис. 84). Расстояния от источника стоячей волны до пучностей равны: 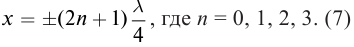
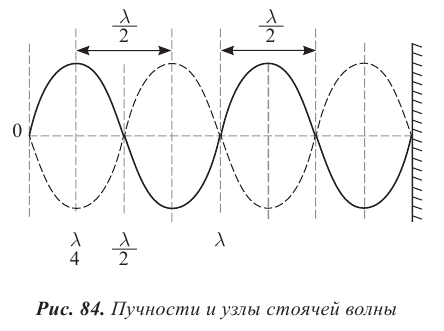
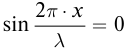 образуются узлы, амплитуда колебаний в этой точке равна 0. Расстояния от источника волны до узлов равны:
образуются узлы, амплитуда колебаний в этой точке равна 0. Расстояния от источника волны до узлов равны:

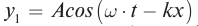 . Уравнение отраженной волны:
. Уравнение отраженной волны: 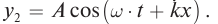
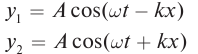
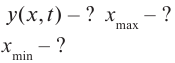
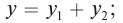
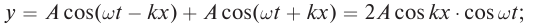
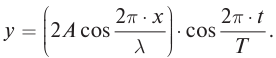
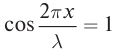 образуется пучность с амплитудой 2А. Расстояние от источника до пучностей
образуется пучность с амплитудой 2А. Расстояние от источника до пучностей 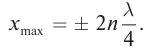
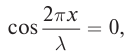 тогда
тогда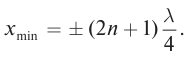
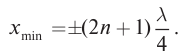

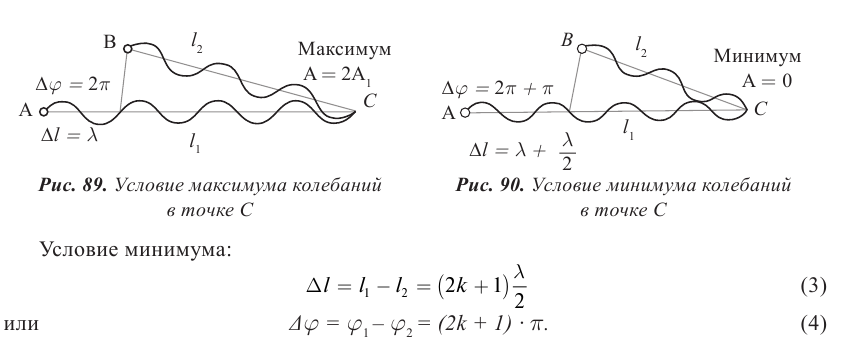
 от точки С, достаточно определить разность хода волн и сравнить с длиной волны. Если разность хода равна целому числу длин волн, то в точке С произойдет наложение гребней или впадин, амплитуда колебаний возрастет (рис. 89). Выполняется условие максимума:
от точки С, достаточно определить разность хода волн и сравнить с длиной волны. Если разность хода равна целому числу длин волн, то в точке С произойдет наложение гребней или впадин, амплитуда колебаний возрастет (рис. 89). Выполняется условие максимума: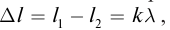
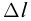 − разность хода волн,
− разность хода волн, 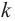 – натуральное число, равное 0, 1, 2, 3 … Разность хода лучей соответствует разности фаз колебаний:
– натуральное число, равное 0, 1, 2, 3 … Разность хода лучей соответствует разности фаз колебаний:
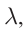 периоду Т соответствует фаза
периоду Т соответствует фаза 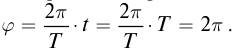

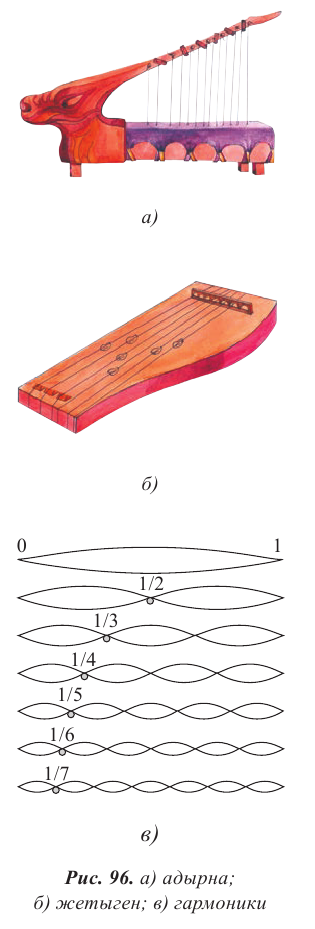
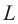 струны равняется целому числу длин полуволн:
струны равняется целому числу длин полуволн: 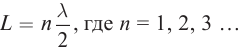
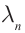 длин волн соответствует набор возможных частот
длин волн соответствует набор возможных частот 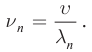 Каждая из частот
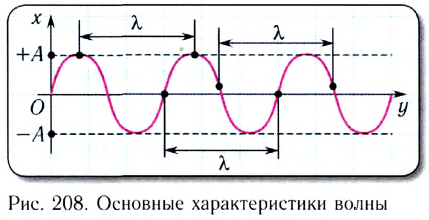
Каждая из частот 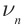 и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота называется основной частотой, все остальные частоты называются гармониками.
и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота называется основной частотой, все остальные частоты называются гармониками.

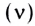 — число полных колебаний в данной точке в единицу времени. Частота волн определяется частотой источника;
— число полных колебаний в данной точке в единицу времени. Частота волн определяется частотой источника;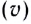 — скорость перемещения гребня волны (это не скорость частиц!):
— скорость перемещения гребня волны (это не скорость частиц!):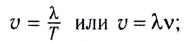
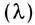 — наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. это расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника
— наименьшее расстояние между двумя точками, колебания в которых происходят в одинаковой фазе, т. е. это расстояние, на которое волна распространяется за промежуток времени, равный периоду колебаний источника 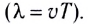
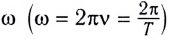 и амплитудой А:
и амплитудой А: 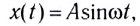
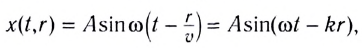
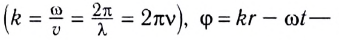 фаза волны.
фаза волны.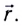
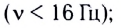
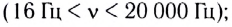
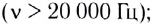
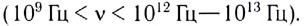
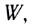 переносимая волной в единицу времени
переносимая волной в единицу времени 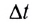 = 1 с через единичную площадку площадью
= 1 с через единичную площадку площадью 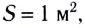 расположенную перпендикулярно к направлению распространения волны:
расположенную перпендикулярно к направлению распространения волны: 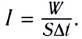
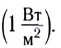
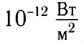 (порог слышимости) до
(порог слышимости) до 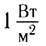 (порог болевого ощущения). Человек может слышать и более интенсивные звуки, но при этом он будет испытывать боль.
(порог болевого ощущения). Человек может слышать и более интенсивные звуки, но при этом он будет испытывать боль.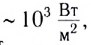 мощные усилители на концерте в закрытом помещении — до
мощные усилители на концерте в закрытом помещении — до 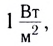 поезд метро — около
поезд метро — около 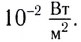
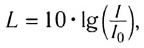
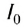 — интенсивность
— интенсивность 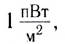 соответствующая минимально возможной интенсивности звука, улавливаемого ухом человека.
соответствующая минимально возможной интенсивности звука, улавливаемого ухом человека.