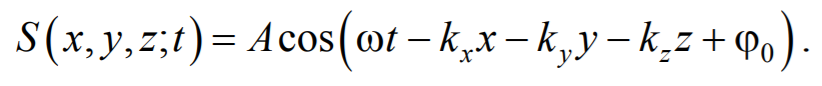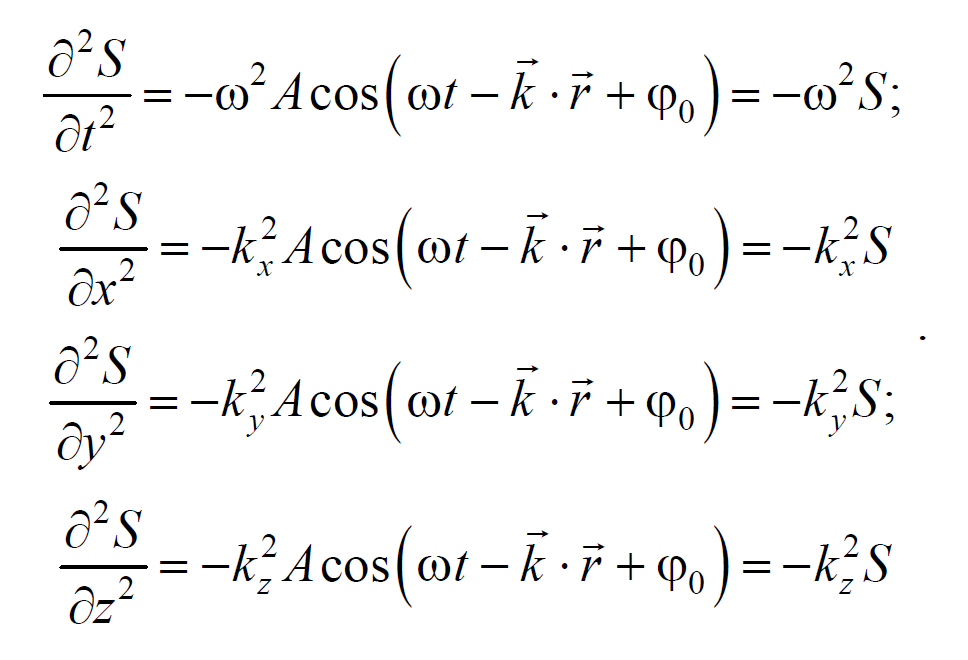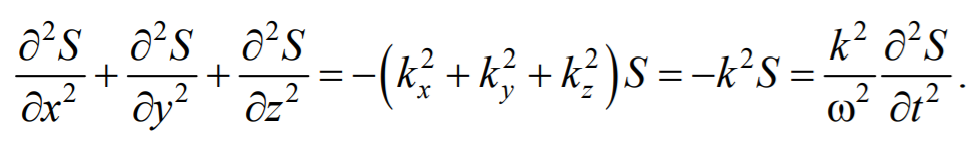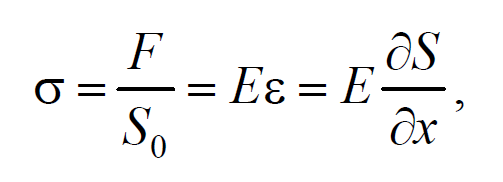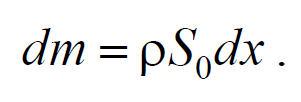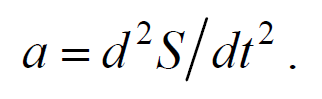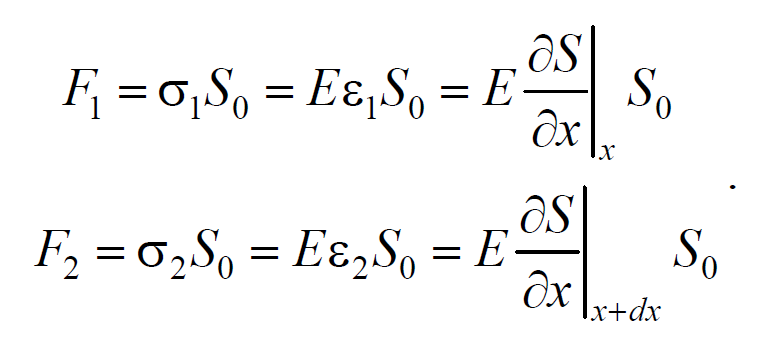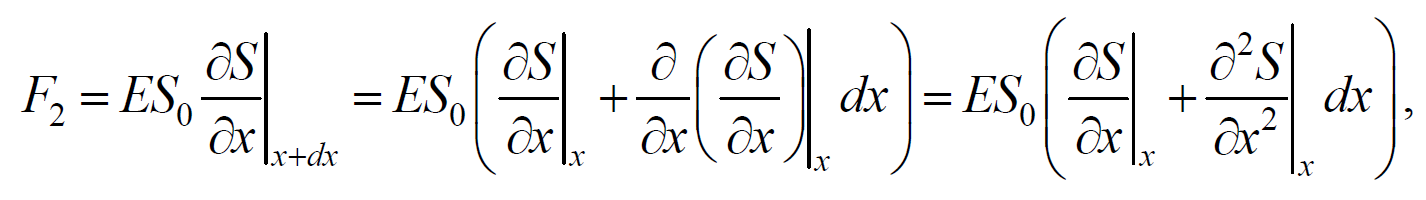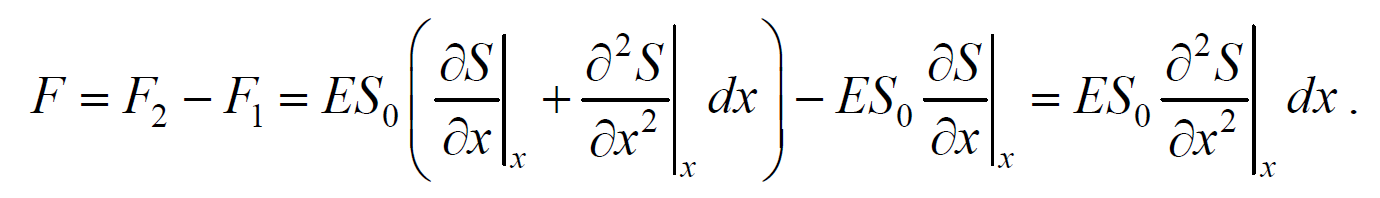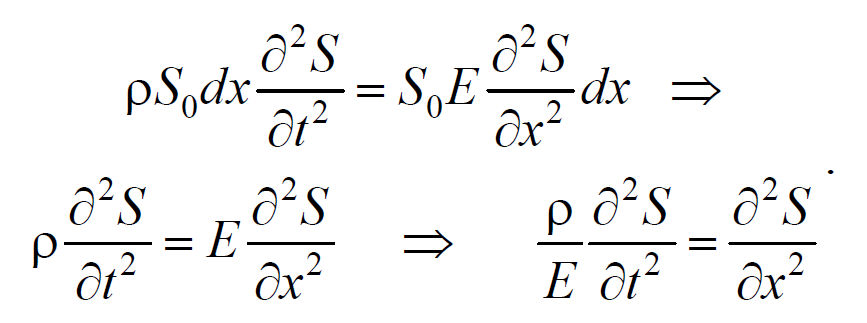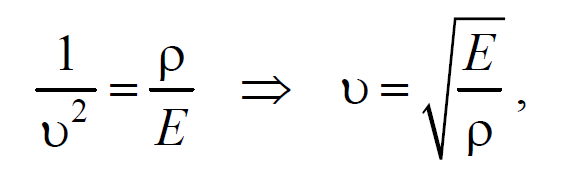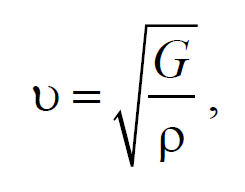| Уравнения плоской и сферической волн |   |
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.
Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид: Уравнение волны можно записать и в другом виде. Введем волновое число
где Так как
Уравнение сферической волны В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна wt (т.е.
где А равна амплитуде на расстоянии от источника равном единице. Уравнение (5.2.7) неприменимо для малых r, т.к. при Содержание Видео:10й класс; Физика; "Уравнение плоской волны"Скачать  Уравнение плоской волны и его параметрыотстоящие друг от друга на расстоянии λ, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции . в случае плоской волны, предполагая, что колебания носят гармонический характер. Пусть колебание точек, лежащих в плоскости x = 0, имеет вид (при начальной фазе ф = 0) Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время τ = х/v. Следовательно, колебания частиц в плоскости x будут отставать по времени на τ от колебаний частиц в плоскости x = 0, т. е. — это уравнение плоской волны (рис. 2.4.3). Таким образом, . есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания A = const. Это будет, если энергия волны не поглощается средой. Такой же вид уравнение (2.4.5) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так: Выражения (2.4.5) и (2.4.6) есть уравнения бегущей волны. Уравнение волны можно записать и в другом виде. Введем волновое число k = 2π/λ, или в векторной форме где k — волновой вектор; n — нормаль к волновой поверхности. Так как λ = vT , то k = 2π/vT = 2πν/v = ω/v. Отсюда v = ω/k. Тогда уравнение плоской волны запишется так: Видео:Получение уравнения плоской бегущей волны.Скачать  Лекция №9. Механические волны6.1. Распространение колебаний в упругой средеМеханические колебания, распространяющиеся в упругой среде (твердой, жидкой или газообразной), называются механическими или упругими волнами . Процесс распространения колебаний в сплошной среде называется волновым процессом или волной. Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение. Они лишь совершают колебания около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества . В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны. Упругая волна называется продольной , если колебания частиц среды происходят в направлении распространения волны. Продольные волны связаны с объемной деформацией растяжения − сжатия среды, поэтому они могут распространяться как в твердых телах, так и в жидкостях и газообразных средах.
На рис. 6.1.1 представлена гармоническая поперечная волна, распространяющаяся вдоль оси 0х . График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны . Длина волны также равна тому расстоянию, на которое распространяется определенная фаза колебания за период колебаний Колеблются не только частицы, расположенные вдоль оси 0х , а совокупность частиц, заключенных в некотором объеме. Геометрическое место точек, до которых доходят колебания к моменту времени t , называется фронтом волны . Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью . Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, а в сферической − множество концентрических сфер. 6.2. Уравнение плоской волныУравнением плоской волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x , y , z и времени t Эта функция должна быть периодической как относительно времени t , так и относительно координат x , y , z . Периодичность по времени вытекает из того, что смещение S описывает колебания частицы с координатами x , y , z , а периодичность по координатам следует из того, что точки, отстоящие друг от друга на расстоянии, равном длине волны, колеблются одинаковым образом. Предположим, что колебания носят гармонический характер, а ось 0х совпадает с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны оси 0х и, поскольку все точки волновой поверхности колеблются одинаково, смещение S будет зависеть только от координаты х и времени t Рассмотрим некоторую частицу среды, находящуюся от источника колебаний О на расстоянии х . Пусть колебания точек, лежащих в плоскости х = 0 имеют вид Найдем вид колебания точек в плоскости, соответствующей произвольному значению х . Для того, чтобы пройти путь от плоскости х = 0 до плоскости х , волне требуется время τ = x/υ . Следовательно, колебания частиц, лежащих в плоскости х , будут отставать по времени на τ от колебаний частиц в плоскости х = 0 и описываться уравнением где А − амплитуда волны; ϕ0 − начальная фаза волны (определяется выбором начал отсчета х и t ). Зафиксируем какое-либо значение фазы ω(t-x/υ)+ϕ0=const. Это выражение определяет связь между временем t и тем местом х , в котором фаза имеет фиксированное значение. Продифференцировав данное выражение, получим Таким образом, скорость распространения волны есть скорость перемещения фазы, и называется фазовой скоростью . При υ > 0 волна распространяется в сторону возрастания х . Волна, распространяющаяся в противоположном направлении, описывается уравнением Придадим уравнению плоской волны симметричный относительно х и t вид. Для этого введем величину $$k = $$ , которая называется волновым числом , которое можно представить в виде Тогда уравнение плоской волны будет иметь вид Мы предполагали, что амплитуда колебаний не зависит от х . Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. При распространении в поглощающей энергию среде интенсивность волны с удалением от источника колебаний постепенно уменьшается, т. е. наблюдается затухание волны. В однородной среде такое затухание происходит по экспоненциальному закону A=A0e −βx . Тогда уравнение плоской волны для поглощающей среды имеет вид 6.3. Волновое уравнениеУравнение плоской волны, распространяющейся в произвольном направлении, будет иметь вид где r − радиус-вектор, точки волны; r =k× n − волновой вектор ; n − единичный вектор нормали к волновой поверхности Волновой вектор − это вектор, равный по модулю волновому числу k и имеющий направление нормали к волновой поверхности называется. Перейдем от радиус-вектора точки к ее координатам x , y , z Установим вид волнового уравнения. Для этого найдем вторые частные производные по координатам и времени выражение (6.3.3) Сложив производные по координатам, и с учетом производной по времени, получим 6.4. Скорость распространения волн в различных средахДля определения скорости упругих волн в упругой среде рассмотрим продольную плоскую волну, распространяющуюся в направлении оси 0х . Выделим в среде цилиндрический объем с площадью основания S0 и высотой dx . Смещения S частиц с разными х в каждый момент времени оказываются различными. Если основание цилиндра с координатой х имеет в некоторый момент времени смещение S , то смещение основания с координатой x+dx будет S+dS . Тогда, рассматриваемый объем деформируется и получает удлинение dS или относительную деформацию ε=∂S/∂x (деформации растяжения). Наличие деформации свидетельствует о существовании нормального напряжения σ , которое при малых деформациях пропорционального величине деформации. По закону Гука для деформации растяжения − сжатия где Е − модуль Юнга среды. Из зависимости смещения от координаты x видно, что относительная деформация ∂S/∂x , а также, и напряжение σ в фиксированный момент времени зависят от х . В соответствии с этим, продольная волна состоит из чередующихся разрежений и сжатий среды. Теперь для цилиндрического объема запишем уравнение движения. Масса этого объема где ρ − плотность недеформированной среды. Ввиду малости dx можно считать ускорение всех точек цилиндра одинаковым и равным Тогда этот участок объема будет растянут под влиянием сил F1 и F2 , приложенных к основаниям цилиндра в данный момент времени. Силы, действующие на левое и правое основание цилиндра равны, соответственно После разложения силы F2 в ряд, получим и результирующая F1 , F2 сил, действующая на элемент объема равна Используя основное уравнение динамики поступательного движения (2.1.2) и, подставив значения массы, ускорения и силы, получим Из сравнения этого уравнения с волновым уравнением для плоской волны (6.3.6) $$=$$ , получим где Е − модуль Юнга. Полученное уравнение определяет фазовую скорость продольных упругих волн. Если проделать аналогичные преобразования для поперечных упругих волн, то фазовая скорость поперечных упругих волн будет иметь следующий вид 💡 ВидеоУрок 370. Механические волны. Математическое описание бегущей волныСкачать  4.3 Плоские электромагнитные волны в идеальных диэлектрических средахСкачать  Билет №34 "Электромагнитные волны"Скачать  Механические модели волн. 1.Скачать  Уравнения и графики механических гармонических колебаний. 11 класс.Скачать  Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать  Урок 374. Энергия, переносимая волной. Интенсивность сферической волныСкачать  4.2 Решение волновых уравнений Гельмгольца в виде плоских бегущих волнСкачать  Билеты № 35, 39 "Плоская волна, ее отражение. Давление излучения"Скачать  74. Упругие волныСкачать  МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать  Упругие механические волны. 1 часть. 11 класс.Скачать  Волновое движение. Механические волны. 9 класс.Скачать  МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать  Физика 11 класс (Урок№2 - Механические волны.)Скачать  4.7 Характеристики плоских однородных электромагнитных волнСкачать  Урок 95 (осн). Механические волны. ЗвукСкачать  Лекция 2 ВолныСкачать  |

 .
. . Пусть колебание точек, лежащих в плоскости
. Пусть колебание точек, лежащих в плоскости  , имеет вид (при начальной фазе
, имеет вид (при начальной фазе  )
)

 .
. ,
, . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой. , или
, или  .
. .
. , или в векторной форме:
, или в векторной форме: ,
, – волновой вектор,
– волновой вектор,  – нормаль к волновой поверхности.
– нормаль к волновой поверхности. , то
, то  . Отсюда
. Отсюда  . Тогда уравнение плоской волны запишется так:
. Тогда уравнение плоской волны запишется так: .
. ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу  . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону  . Следовательно, уравнение сферической волны:
. Следовательно, уравнение сферической волны: , или
, или  ,
, , амплитуда стремится к бесконечности. То, что амплитуда колебаний
, амплитуда стремится к бесконечности. То, что амплитуда колебаний  , следует из рассмотрения энергии, переносимой волной.
, следует из рассмотрения энергии, переносимой волной.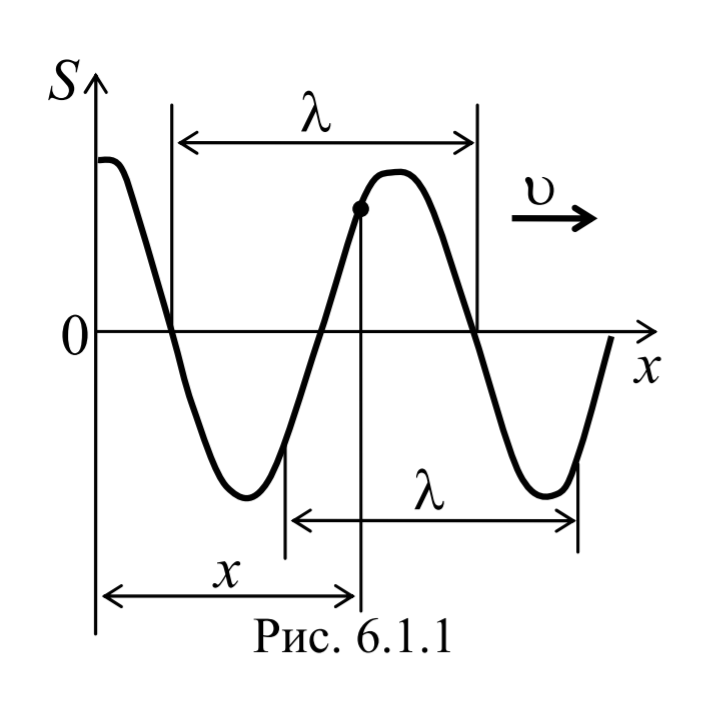 Упругая волна называется поперечной , если колебания частиц среды происходят в плоскостях, перпендикулярных к направлению распространения волны Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т. е. способна сопротивляться деформации сдвига. Этим свойством обладают только твердые тела.
Упругая волна называется поперечной , если колебания частиц среды происходят в плоскостях, перпендикулярных к направлению распространения волны Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т. е. способна сопротивляться деформации сдвига. Этим свойством обладают только твердые тела.
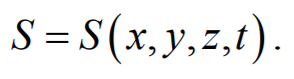
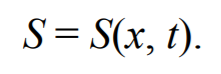
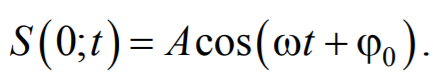
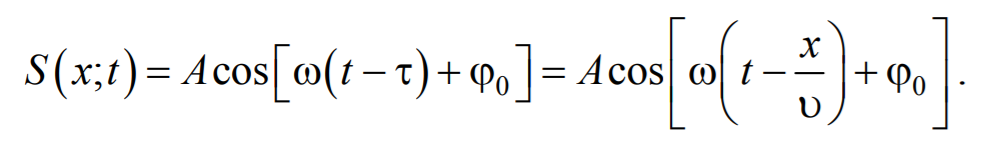
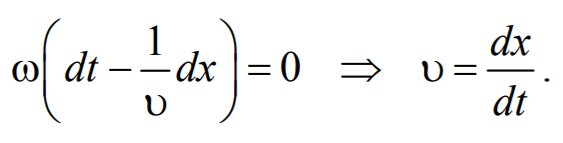

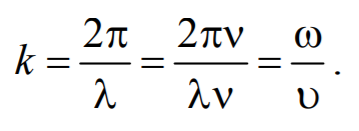
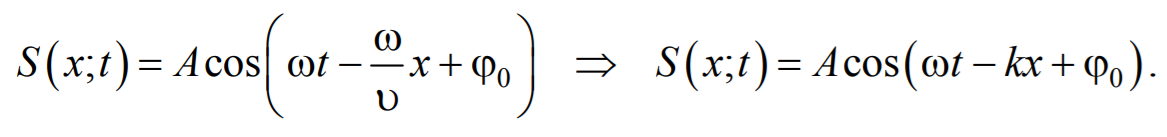
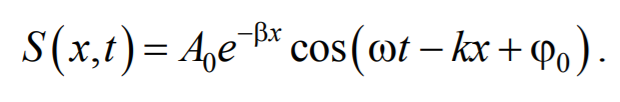
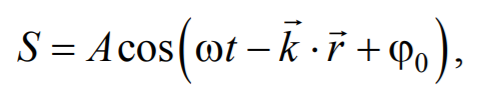
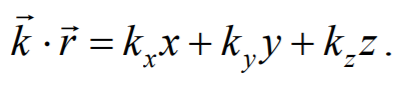 Тогда уравнение (6.3.2) примет вид
Тогда уравнение (6.3.2) примет вид