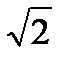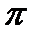Уравнение упругой волны — это зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при похождении в ней рассматриваемой волны. При распространении в упругой среде механических возмущений, возбуждаемых источником волн, происходит перенос энергии, поэтому такие волны называют бегущими волнами.
Упругая волна называется синусоидальной или гармонической, если соответствующие ей колебания частиц среды являются гармоническими.
Геометрическое место точек, в которых фаза колебаний имеет одно и то же значение, называется волновой поверхностью. Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу.
Уравнение плоской волны, распространяющейся вдоль оси ОХ в непоглощающей среде, можно записать в виде:
Здесь s — величина, характеризующая колебательное движение среды; и — скорость распространения волны. Колебания в некоторой точке отличаются от колебаний в начале координат (О) сдвигом по времени
Уравнение плоской синусоидальной волны, распространяющейся в непоглощающей среде вдоль положительного направления оси ОХ, имеет вид:
Здесь А — амплитуда волны; со = —— циклическая частота волны,
Т — период колебаний; ср0 — начальная фаза колебаний в точках координатной плоскости х = 0; (р = ( + ср0) — фаза плоской волны.
Расстояние X = х>Т, на которое распространяется синусоидальная волна за время, равное периоду колебаний, называется длиной волны. Длина волны X равна расстоянию между двумя ближайшими точками среды, для которых разность фаз колебаний равна 2л.
Еще одна характеристика синусоидальной волны — волновое число к, которое численно равно количеству длин волн, укладывающихся на отрезке длиной 2л.
Уравнение плоской синусоидальной волны (4.3.2) можно также записать в виде:
Волновым вектором называется вектор к, по модулю равный волновому числу к и направленный вдоль луча в рассматриваемой точке. Лучом называется линия, касательная к которой в каждой ее точке совпадает с направлением распространения волны, т. е. с направлением переноса энергии волной.
Волновой вектор плоской синусоидальной волны не зависит от выбора точки. Для плоской синусоидальной волны, распространяющейся вдоль положительного направления оси ОХ, выражение (4.3.4) можно записать в виде:
Здесь к — ki, кх = кг, где г — радиус-вектор, определяющий положение равновесия колеблющейся точки среды.
Волна называется сферической, если ее волновые поверхности имеют вид концентрических сфер; такие волны возбуждаются в однородной изотропной среде уединенным точечным источником. Центр этих сфер называется центром волны.
Для синусоидальной сферической волны запишем:
где А(г) — амплитуда волны; ср0 — начальная фаза колебаний в центре волны.
Можно доказать, что при распространении сферической волны в непоглощающей среде амплитуда волны удовлетворяет соотношению:

где а0 — физическая величина, численно равна амплитуде волны на расстоянии г = 1 м от центра волны.
В линейной однородной, изотропной, непоглощающей среде волны описываются дифференциальным уравнением в частных производных, которое называется волновым уравнением и имеет вид:
Скорость v распространения синусоидальной волны называется фазовой скоростью. Эта скорость равна скорости перемещения в пространстве точек поверхности, соответствующей любому фиксированному значению фазы синусоидальной волны.
Например, для случая плоской синусоидальной волны, задавая фиксированное значение фазы волны, cot — кх + ср0 = const, найдем производную от координаты по времени, т. е. скорость:
Можно получить, что скорость продольной волны в однородной газообразной среде определяется выражением:
где р — плотность газа (р = const), К — модуль объемной упругости газа.
Скорость поперечных упругих волн в неограниченной изотропной твердой среде
Здесь G — модуль сдвига среды, р — плотность среды.
Распространение продольных волн в тонком стержне связано с его продольным растяжением и сжатием. Для скорости продольных волн в тонком стержне можно получить, используя модуль Юнга Е для материала стержня,
Скорость распространения поперечных волн в натянутой тонкой нити (в струне) зависит от натяжения струны и определяется выражением:
где F — сила натяжения струны; р — плотность материала струны; Sceч — площадь ее поперечного сечения.
Заметим, что упругие свойства и плотность твердых тел и жидкостей зависят от химического состава и мало изменяются при различных давлениях и температурах.
Приближенно можно считать, что скорость упругих волн в твердых телах и в жидкостях постоянна.
Модуль объемной упругости К газа зависит от вида термодинамического процесса его объемной деформации, поэтому скорость упругих волн в идеальном газе зависит от частоты волн (дисперсия волн). Колебания частиц среды при распространении в ней упругих волн совершаются с той же частотой, что и колебания источника волн.
Будем считать, что при очень быстрой деформации, т. е. при достаточно большой частоте колебаний частиц среды (газа), реализуется адиабатический процесс.
Тогда можно получить выражение для скорости упругих волн в идеальном газе при адиабатическом процессе.
где у — показатель адиабаты; R — универсальная газовая постоянная, Т — температура, М- молярная масса.
Из опытов скорость слышимых звуковых волн в газах слабо зависит от частоты и может определиться выражением (4.3.9), если плотность газов не велика.
Видео:10й класс; Физика; "Уравнение плоской волны"Скачать

Волновая природа света
| Название | Волновая природа света |
| Анкор | FEPO_2005_fizika_-_moi_otvety.docx |
| Дата | 03.11.2017 |
| Размер | 193.97 Kb. |
| Формат файла |  |
| Имя файла | FEPO_2005_fizika_-_moi_otvety.docx |
| Тип | Документы #10071 |
| страница | 3 из 3 |
| Подборка по базе: 2-2 ИДЗ Волновая оптика+Теплов.излучение 25 вар_5 зад 2017г .do, Урок-КВН. Природа вокруг нас..docx, Эта удивительная природа..doc, 7. Путешествуем вокруг света.doc, 7 кл-ЗАКОН И ПРИРОдА.docx, Кроссворд Природа Алтая.docx, статья Он весь дитя добра и света.docx, Влияние света тепла и влаги на рост растений.docx, быть может вся природа мозаика цветов.docx, ОВЗ природа.docx 1. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ, имеет вид 2. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ, имеет вид 3. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ со скоростью 500 м/с, имеет вид 4. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ со скоростью 500 м/с, имеет вид 5. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси OХ, имеет вид Уравнение гармонических колебаний 1. Материальная точка совершает гармонические колебания с амплитудой А=4см и периодом Т=2с. Если смещение точки в момент времени, принятый за начальный, равно своему максимальному значению, то точка колеблется в соответствии с уравнением (в СИ)… С) 2. Материальная точка совершает гармонические колебания с амплитудой А=4см и частотой =2Гц. Если смещение точки в момент времени, принятый за начальный, равно нулю, то точка колеблется в соответствии с уравнением (в СИ)… d) 3. Материальная точка совершает гармонические колебания с амплитудой А=4см и частотой =2Гц. Если смещение точки в момент времени, принятый за начальный, равно своему максимальному значению, то точка колеблется в соответствии с уравнением (в СИ)… 4. Материальная точка совершает гармонические колебания с амплитудой А=4см и периодом Т=2с. Если смещение точки в момент времени, принятый за начальный, равно 2см, то точка колеблется в соответствии с уравнением (в СИ)… 5. Материальная точка совершает гармонические колебания с амплитудой А=4см и частотой =2Гц. Если смещение точки в момент времени, принятый за начальный, равно 2см, то точка колеблется в соответствии с уравнением (в СИ)… Уравнение Шредингера (конкретные ситуации) 1. Вероятность обнаружить электрон на участке (a,b) одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле (Считает по интегралу в зависимости от заданных границ) Уравнения свободных и вынужденных колебаний 1. Уравнение движения пружинного маятника Решение: 1) Вынужденные колебания: 2) Свободные затухающие колебания: 3) Свободные незатухающие колебания: 4. Свободные затухающие колебания заряда конденсатора в колебательном контуре описываются уравнением… 5. Вынужденные колебания заряда конденсатора в колебательном контуре описываются уравнением… Уравнения Шредингера (общие свойства) 1. Стационарным уравнением Шредингера для частицы в трехмерном ящике с бесконечно высокими стенками является уравнение… 2. Стационарным уравнением Шредингера для частицы в одномерном ящике с бесконечно высокими стенками является уравнение…c) 3. Стационарным уравнением Шредингера для электрона в водородоподобном ионе является уравнение… 4. Нестационарным уравнением Шредингера является уравнение… 1. На рисунке представлены две вольтамперные характеристики вакуумного фотоэлемента. Если Е – освещенность фотокатода, а – частота падающего на него света, то справедливо следующее утверждение… # 2. На рисунке представлены две вольтамперные характеристики вакуумного фотоэлемента. Если Е – освещенность фотокатода, а – длина волны падающего на него света, то справедливо следующее утверждение… 3. На рисунке представлены две вольтамперные характеристики вакуумного фотоэлемента. Если Е – освещенность фотокатода, а – длина волны падающего на него света, то справедливо следующее утверждение… 4. На рисунке представлены две вольтамперные характеристики вакуумного фотоэлемента. Если Е – освещенность фотокатода, а – длина волны падающего на него света, то справедливо следующее утверждение… Энергия волны. Перенос энергии волной 1. На рисунке показана ориентация векторов напряженности электрического ( 3. На рисунке показана ориентация векторов напряженности электрического () и магнитного () полей в электромагнитной волне. Вектор плотности потока энергии электромагнитного поля ориентирован в направлении…
5. На рисунке показана ориентация векторов напряженности электрического () и магнитного () полей в электромагнитной волне. Поток энергии электромагнитного поля ориентирован в направлении…
6. При увеличении в 2 раза амплитуды колебаний векторов напряженности электрического и магнитного полей плотность потока энергии … a) увеличится в 4 раза 7. При уменьшении в 2 раза амплитуды колебаний векторов напряженности электрического и магнитного полей плотность потока энергии …c) уменьшится в 4 раза 8. Если увеличить в 2 раза объемную плотность энергии и при этом увеличить в 2 раза скорость распространения упругих волн, то плотность потока энергии…b) увеличится в 4 раза 9. Если уменьшить в 2 раза объемную плотность энергии при неизменной скорости распространения упругих волн, то плотность потока энергии… b) уменьшится в 4 раза 10. Если увеличить в 2 раза объемную плотность энергии и при этом уменьшить в 2 раза скорость распространения упругих волн, то плотность потока энергии…a) останется неизменной 11. Плотность потока электромагнитной энергии имеет размерность…d) В·А/м 2 12. Плотность потока энергии упругой волны имеет размерность…c) Дж/м 2 Эффект Комптона. Световое давление 1. На рисунке показаны направления падающего фотона (), рассеянного фотона (’) и электрона отдачи (e). Угол рассеяния 90°, направление движения электрона отдачи составляет с направлением падающего фотона угол Решение 2. На рисунке показаны направления падающего фотона (), рассеянного фотона (’) и электрона отдачи (e). Угол рассеяния 90°, направление движения электрона отдачи составляет с направлением падающего фотона угол . Если импульс электрона отдачи Pе, то импульс падающего фотона равен… 3. На рисунке показаны направления падающего фотона (), рассеянного фотона (’) и электрона отдачи (e). Угол рассеяния 90°, направление движения электрона отдачи составляет с направлением падающего фотона угол . Если импульс электрона отдачи Pе, то импульс рассеянного фотона равен… 5. Если увеличить в 2 раза объемную плотность световой энергии, то давление света …b) увеличится в 2 раза 6. Если зачерненную пластинку, на которую падает свет, заменить на зеркальную той же площади, то световое давление …c) увеличится 2 раза 7. Если зеркальную пластинку, на которую падает свет, заменить на зачерненную той же площади, то световое давление … b) уменьшится 2 раза Видео:Получение уравнения плоской бегущей волны.Скачать  Дисциплина: Физика тема: 060 Механические колебания и волны (стр. 3 )
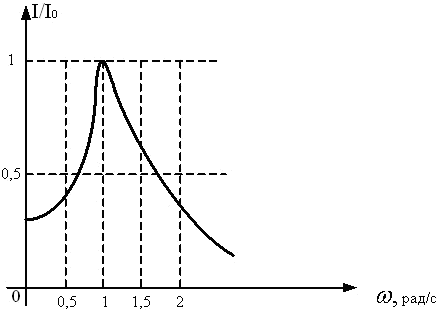
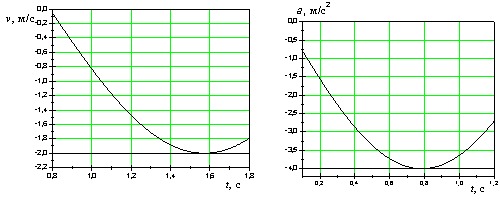
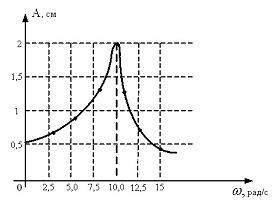
2) ∆ц = 3) ∆ц = 16. [Уд1] (ВО1) Два гармонических колебания происходят с одинаковыми периодами в одном направлении с амплитудами А1 = 4 см и А2 = 3 см. Разность фаз складываемых колебаний равна ∆ц = Тема: 060 Механические колебания и волны V064 – П Волновое движение S064 – П Волновое движение — 10 заданий 1. [Уд1] (ВО1) Решением волнового уравнения 1) 2) 3) 4) 2. [Уд1] (ВО1) Уравнение плоской синусоидальной волны, распространяющейся вдоль оси Ох со скоростью v = 500 м/с, имеет вид о = 0,01 sin (щt – 2х). Циклическая частота щ равна … рад·с-1. 3. [Уд1] (ВО1) Уравнение плоской монохроматической волны ξ, которая распространяется вдоль положительного направления оси Ох представлено формулой 1) 2) 3) 4) 4. [Уд1] (ВО1) Уравнение сферической монохроматической волны ξ представлено формулой 1) 2) 3) 4) 5. [Уд1] (ВО1) Уравнение стоячей волны ξ представлено формулой 1) 2) 3) 4) 6. [Уд1] (ВО1) При интерференции двух волн результирующая волна характеризуется изменением 1) частоты волны 3) распределения энергии в пространстве 4) периода колебаний 7. [Уд1] (ВО1) Источник колебаний, находится в упругой среде, и точки этой среды находятся на расстоянии 8. [Уд1] (ВО1) Если разность фаз колебаний источника волн в упругой среде равна 9. [Уд1] (О) Точки пространства, в которых амплитуда колебаний стоячей волны, равна нулю, называются … стоячей волны. 10. [Уд1] (ВО1) В стоячей волне расстояния между двумя соседними пучностями равно C064 – П Волновое движение (графики) – 4 задания 1. [Уд1] (ВО1) В упругой среде в положительном направлении оси 0x распространяется плоская волна. На рисунке приведен график зависимости смещения о частицы среды от времени t в произвольной точке оси 0х. Циклическая частота волны … рад/c. 2. [Уд1] (ВО1) В упругой среде в положительном направлении оси 0x распространяется плоская волна. На рисунке приведен график зависимости смещения о частицы среды от времени t в произвольной точке оси 0х. Если длина волны равна 40 м, то скорость распространения составляет … м/c. 3. [Уд1] (ВО1) На рисунке приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t = 6 с. Источник колебаний находится в точке с координатой х = 0. В начальный момент времени (t = 0) все частицы среды находились в покое. Фазовая скорость волны равна … м/c. 4. [Уд1] (ВО1) На рисунке приведена моментальная «фотография» модели плоской поперечной гармонической волны в момент времени t = 6 с. Источник колебаний находится в точке с координатой х = 0. В начальный момент времени (t = 0) все частицы среды находились в покое. Циклическая частота волны равна … рад/c. Тема: 240 Электромагнитная индукция Видео:Математика без Ху!ни. Уравнение плоскости.Скачать  v241П Электромагнитная индукция. Закон Фарадеяs241 Сингл П (Магнитный поток, самоиндукция, индуктивность, энергия МП) – 19 заданий1. [Уд1] (О) Неподвижный проводящий контур находится в изменяющемся со временем магнитном поле. Вызывают появление ЭДС индукции в контуре силы … электрического поля. 2. [Уд1] (ВО1) Линии индукции магнитного поля пронизывают рамку площадью S = 0,5 м2 под углом б = 30° к ее плоскости, создавая магнитный поток, равный Ф = 2 Вб. Модуль индукции магнитного поля равен … Тл. 3. [Уд1] (ВО1) Потокосцепление, пронизывающее катушку, концы которой соединены между собой, сопротивлением R в магнитном поле равно Ψ1. При изменении направления вектора магнитной индукции 1) 2) 3) 4. [Уд1] (ВО1) Магнитный поток Φ, сцепленный с проводящим контуром, изменяется со временем так, как показано на рисунке под номером 1. График, соответствующий зависимости от времени ЭДС индукции εi, возникающей в контуре представлен на рисунке 5. [Уд1] (ВО1) В одной плоскости с прямолинейным проводником, по которому течет возрастающий со временем ток, находится проволочная квадратная рамка. Индукционный ток в рамке направлен 1) по часовой стрелке 2) против часовой стрелки 3) индукционный ток в рамке не возникает 4) направление может быть любым 6. [Уд1] (ВОМ) Для получения ЭДС индукции в проводящем контуре, находящемся в магнитном поле, можно изменять со временем: 1) площадь контура; 2) угол между нормалью к плоскости контура и вектором 3) модуль вектора Силы Лоренца являются сторонними силами в случаях 7. [Уд1] (ВО1) По обмотке соленоида индуктивностью L = 0,20 Гн течет ток силой I = 10 А. Энергия W магнитного поля соленоида равна ….… Дж. 8. [Уд1] (ВО1) Проводник длиной l = 1,0 м движется со скоростью v = 5,0 м/с перпендикулярно к линиям индукции однородного магнитного поля. Если на концах проводника возникает разность потенциалов U = 0,02 В, то индукция магнитного поля В равна 9. [Уд1] (ВО1) Магнитный поток Φ, сцепленный с проводящим контуром, изменяется со временем так, как показано на рисунке под номером 1. График, соответствующий зависимости от времени ЭДС индукции εi, возникающей в контуре, представлен на рисунке под номером Видео:9 класс, 35 урок, Длина волны. Скорость распространения волнСкачать  Колебания и волныУравнение движения пружинного маятника свободных незатухающих колебаний Уравнение движения пружинного маятника При сложении двух гармонических колебаний одного направления с одинаковыми периодами и равными амплитудами результирующее колебание имеет такую же амплитуду, что и складываемые колебания. При этом разность фаз исходных колебаний равна . Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной . Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами A0. При разности фаз Складываются два гармонических колебания одного направления с одинаковыми частотами и равными амплитудами Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ со скоростью 500 м/с, имеет вид Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 3,14 Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 6,28 Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 500 Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ со скоростью 500 м/с, имеет вид 1000 Свободные незатухающие колебания заряда конденсатора в колебательном контуре описываются уравнением. Вынужденные колебания заряда конденсатора в колебательном контуре описываются уравнением . Уравнение движения пружинного маятника свободных затухающих колебаний Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 500 Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами А А Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет минимальную амплитуду при разности фаз, равной . Если увеличить в 2 раза объемную плотность энергии и при этом увеличить в 2 раза скорость распространения упругих волн, то плотность потока энергии . увеличится в 4 раза На рисунках изображены зависимости от времени координаты и скорости материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний точки равна . На рисунках изображены зависимости от времени координаты и ускорения материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний точки равна . Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет минимальную амплитуду при разности фаз, равной . Сейсмическая упругая волна, падающая со скоростью 5,6 км/с под углом 45° на границу раздела между двумя слоями земной коры с различными свойствами, испытывает преломление, причем угол преломления равен 30°. Во второй среде волна будет распространяться со скоростью . На рисунке представлена зависимость относительной амплитуды колебаний силы тока в катушке индуктивностью1 мГн, включенной в идеальный колебательный контур. Емкость конденсатора этого контура равна . На рисунках изображены зависимости от времени скорости и ускорения материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний точки равна .
2 с -1 Сейсмическая упругая волна, падающая под углом 45° на границу раздела между двумя слоями земной коры с различными свойствами, испытывает преломление, причем угол преломления равен 30°. Во второй среде волна распространяется со скоростью 4,0 км/с. В первой среде скорость волны была равна . На рисунке представлена зависимость амплитуды колебаний груза на пружине с жесткостью k=10 Н/м от частоты внешней силы. Масса колеблющегося груза равна . Если увеличить в 2 раза объемную плотность энергии и при этом уменьшить в 2 раза скорость распространения упругих волн, то плотность потока энергии . 📺 ВидеоУрок 370. Механические волны. Математическое описание бегущей волныСкачать  Билет №34 "Электромагнитные волны"Скачать  Распространение колебаний в среде. Волны | Физика 9 класс #28 | ИнфоурокСкачать  Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать  Урок 374. Энергия, переносимая волной. Интенсивность сферической волныСкачать  Урок 384. Излучение электромагнитных волн.Скачать  Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать  9 класс, 7 урок, Уравнение прямойСкачать  Раскрытие тайн электромагнитной волныСкачать  Распространение звука. Звуковые волны | Физика 9 класс #32 | ИнфоурокСкачать  Урок 454. Понятие о волновой функцииСкачать  Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Распространение волн в упругих средах. Звуковые волны | Физика 11 класс #18 | ИнфоурокСкачать  Система сходящихся сил. Решение задач по МещерскомуСкачать  Уравнение, которое меняет взгляд на мир [Veritasium]Скачать ![Уравнение, которое меняет взгляд на мир [Veritasium]](https://i.ytimg.com/vi/DH1cv0Rdf2w/0.jpg) Теория поля 12. Рассеяние электромагнитных волн волнСкачать  |













 . Длина волны (в м) равна…
. Длина волны (в м) равна… . Волновое число k (в м -1 ) равно…
. Волновое число k (в м -1 ) равно… . Циклическая частота в (с -1 ) равна…
. Циклическая частота в (с -1 ) равна… . Длина волны (в м) равна …
. Длина волны (в м) равна …




 , где
, где  – плотность вероятности, определяемая
– плотность вероятности, определяемая  -функцией. Если
-функцией. Если  -функция имеет вид, указанный на рисунке, то вероятность обнаружить электрон на участке
-функция имеет вид, указанный на рисунке, то вероятность обнаружить электрон на участке является дифференциальным уравнением …
является дифференциальным уравнением … или
или  , где x – смещение колеблющегося тела из положения равновесия; δ=b/m – коэффициент затухания,
, где x – смещение колеблющегося тела из положения равновесия; δ=b/m – коэффициент затухания,  – собственная частота той же колебательной системы, F0 – амплитуда вынуждающей силы, k – коэффициент жёсткости пружины, m – масса тела.
– собственная частота той же колебательной системы, F0 – амплитуда вынуждающей силы, k – коэффициент жёсткости пружины, m – масса тела. или
или  .
. или
или  .
.













 ) и магнитного (
) и магнитного ( ) полей в электромагнитной волне. Вектор плотности потока энергии электромагнитного поля ориентирован в направлении…
) полей в электромагнитной волне. Вектор плотности потока энергии электромагнитного поля ориентирован в направлении…
 a) 4
a) 4 a) 4
a) 4 . Если импульс падающего фотона Pф, то импульс электрона отдачи равен…
. Если импульс падающего фотона Pф, то импульс электрона отдачи равен…
 /
/





 . Амплитуда их результирующего колебания составляет … см.
. Амплитуда их результирующего колебания составляет … см. является уравнение плоской монохроматической волны ξ, которая распространяется вдоль направления оси Ох. Это уравнение представлено формулой
является уравнение плоской монохроматической волны ξ, которая распространяется вдоль направления оси Ох. Это уравнение представлено формулой















 м от источника. Частота колебаний
м от источника. Частота колебаний  Гц, фазовая скорость волны
Гц, фазовая скорость волны  м/с. Разность фаз
м/с. Разность фаз  равна … рад.
равна … рад. = 0,5р рад, и точки этой среды находятся на расстоянии
= 0,5р рад, и точки этой среды находятся на расстоянии  м от источника. Частота колебаний составляет
м от источника. Частота колебаний составляет  Гц, тогда фазовая скорость волны равна … м/с.
Гц, тогда фазовая скорость волны равна … м/с.


 на противоположное, через катушку протекает заряд q. Верное выражение для заряда соответствует формуле
на противоположное, через катушку протекает заряд q. Верное выражение для заряда соответствует формуле




 магнитной индукции;
магнитной индукции; .
.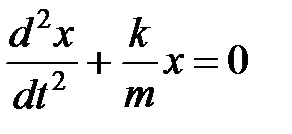 является дифференциальным уравнением .
является дифференциальным уравнением .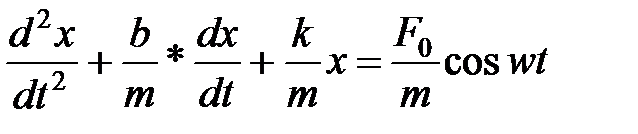 является дифференциальным уравнением .
является дифференциальным уравнением .
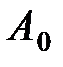 . При разности фаз
. При разности фаз 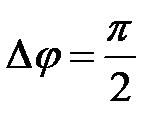 амплитуда результирующего колебания равна .
амплитуда результирующего колебания равна .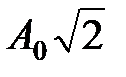
 амплитуда результирующего колебания равна .
амплитуда результирующего колебания равна .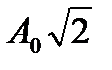
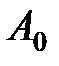 . При разности фаз
. При разности фаз 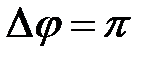 амплитуда результирующего колебания равна .
амплитуда результирующего колебания равна .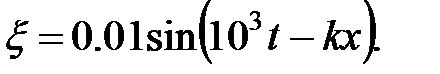 Волновое число
Волновое число 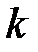 (в м -1 ) равно .
(в м -1 ) равно .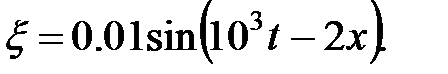 Длина волны (в м) равна .
Длина волны (в м) равна .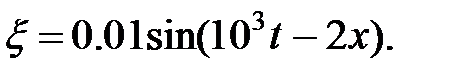 Период (в мс) равен .
Период (в мс) равен .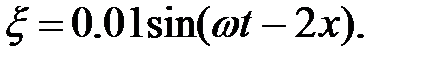 Циклическая частота
Циклическая частота 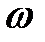 (в с -1 ) равна .
(в с -1 ) равна .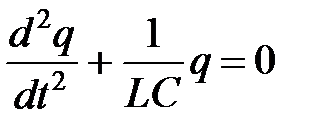
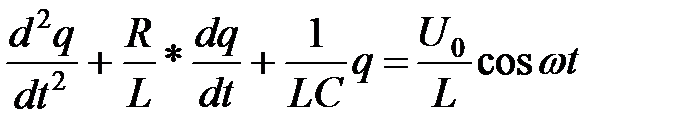
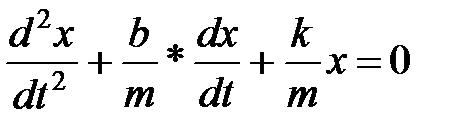 Является дифференциальным уравнением .
Является дифференциальным уравнением .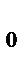 . При разности фаз
. При разности фаз 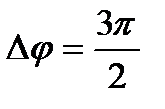 амплитуда результирующего колебания равна .
амплитуда результирующего колебания равна .