Величина  — максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: — максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем:  , а для случая нулевой начальной фазы: , а для случая нулевой начальной фазы:  (см. график). (см. график). |  |
| Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения). | |
Сравним выражения для смещения и ускорения при гармонических колебаниях:  и и  . . | |
Можно записать:  — т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота. — т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота. |
3.2 Представление гармонических колебаний в виде вращающегося вектора. Сложение двух гармонических колебаний с одинаковыми частотами, совершающихся в одном направлении. Условия усиления и максимального усиления колебаний. Условия ослабления и наибольшего ослабления колебаний.
· Гармоническое (то есть синусоидальное) колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствуетамплитуде, угол поворота относительно оси (Ox) — фазе.
Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом (геометрической) суммой [1] (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда — длиной этого вектора, а фаза — углом его поворота относительно Ox.
- Колеблющееся тело может принимать участие в нескольких колебательных процессах, тогда следует найти результирующее колебание, другими словами, колебания необходимо сложить. В данном разделе будем складывать гармонические колебания одного направления и одинаковой частоты

применяя метод вращающегося вектора амплитуды, построим графически векторные диаграммы этих колебаний (рис. 1). Tax как векторы A1 и A2 вращаются с одинаковой угловой скоростью ω0, то разность фаз (φ2 — φ1) между ними будет оставаться постоянной. Значит, уравнение результирующего колебания будет

В формуле (1) амплитуда А и начальная фаза φ соответственно определяются выражениями

Значит, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает при этом также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2 — φ1) складываемых колебаний.
3.3 Квазиупругая сила. Математический и физический маятники. Циклическая частота гармонического осциллятора. Энергия колебаний.
·
Такая зависимость силы от смещения характерна для упругой силы силы. Поэтому силы иной физической природы удовлетворяющие тому же виду зависимости, называются квазиупругими.
· Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит [1] от амплитуды и массы маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо силотносительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:

· гармонический осциллятор — это система, уравнение движения которой описывается дифференциальным уравнением 2 x + ω0 x = 0, ¨ (1) где x — величина, совершающая колебания, ω0 — циклическая частота.
· При механических колебаниях колеблющееся тело (или материальная точка) обладает кинетической и потенциальной энергией.Кинетическая энергия тела W:
·
Для вычисления потенциальной энергии тела воспользуемся самой общей формулой, связывающей силу и потенциальную энергию тела в поле этой силы:
где U — потенциальная энергия, набираемая (или теряемая) телом, движущимся в силовом поле F от точки 0 (точки, в которой потенциальная энергия принимается равной 0) до точки х.
Для силы, линейно зависящей от смещения (как в случае наших механических маятников, такие силы носят общее название квазиупругих сил) мы имеем:

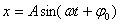

Сравнивая формулы для кинетической и потенциальной энергии, можно сделать выводы:
1. Полная механическая энергия тела не изменяется при колебаниях: 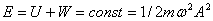
2. Частота колебаний кинетической и потенциальной энергии в 2 раза больше частоты колебаний маятника.
3. Колебания кинетической и потенциальной энергии сдвинуты друг относительно друга по фазе на p (на полпериода). Когда кинетическая энергия достигает максимума, потенциальная — минимума (нуля) и наоборот. Энергия при колебаниях постоянно перекачивается из потенциальной в кинетическую и обратно.
3.4 Упругие (механические) волны. Механизмы и условия возникновения упругих волн. Поперечные и продольные упругие волны, условия их возникновения. Формула скорости упругих волн в различных средах. Длина волны. Циклическое волновое число. Уравнение плоской волны.
Механической волной называется процесс распространения колебаний в упругой среде, который сопровождается передачей энергии от одной точки среды к другой.
Источником механической волны является колеблющее тело. Если источник колеблется синусоидально, то и волна в упругой среде будет иметь форму синусоиды. Колебания, вызванные в каком-либо месте упругой среды, распространяются в среде с определенной скоростью, зависящей от плотности и упругих свойств среды.
Подчеркнем, что при распространении волны отсутствует перенос вещества, т. е. частицы только колеблются вблизи положений равновесия.
Различают продольные и поперечные волны.
Упругая волна называется продольной, если частицы среды колеблются в направлении распространения волны. Продольные волны связаны с объемной деформацией упругой среды и потому могут распространяться в любой среде — твердой, жидкой и газообразной. Примером таких волн являются звуковые волны в воздухе.
Упругая волна называется поперечной, если частицы среды колеблются, оставаясь в плоскостях, перпендикулярных направлению распространения волны. Поперечные волны связаны с деформацией сдвига упругой среды и, следовательно, могут образовываться и распространяться только в средах, обладающих упругостью формы, т. е. в твердых телах. Примером поперечных волн могут, служить волны, распространяющиеся вдоль струн музыкальных инструментов.
Фазовая скорость различна для разных сред. В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:



Фазовая скорость упругих продольных волн в твердом теле равна

где Е — модуль Юнга, 
Фазовая скорость продольных волн в жидкости и газе определяется соотношением:
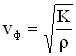

Фазовая скорость продольных волн в идеальном газе задается формулой:




Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой 
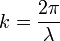
Получить соотношение, связывающее длину волны с фазовой скоростью ( 

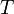
Уравнение плоской волны:
Волна называется плоской , если ее волновые поверхности представляют совокупность плоскостей, параллельных друг другу. В плоской волне , распространяющейся вдоль оси ОХ , все величины s, характеризующие колебательные движение среды, зависят только от времени и координаты х точки М среды. Колебания происходят по закону s=f(t), но сдвинуты во времени на xv. Поэтому ур-ие плоской волны имеет вид: s=f(t-xv). Синусоидальная волна:
s=Asin(-t-wxv+w0). A=const – амплитуда колебаний (амплит. волны). j=2wT.
3.5 энергетические характеристики волн: объёмная плотность энергии волны, поток энергии волны, плотность потока энергии волны, интенсивность волны, спектральная плотность потока энергии излучения. Уровень интенсивности, уровень звукового давления, уровень громкости звука.
При волновом движении происходит перенос энергии, которая состоит из кинетической и потенциальной энергий колеблющихся частиц среды. Причем потенциальная энергия обусловлена деформацией вещества при взаимном смещении частиц. В отличие от колебаний свободного тела в волне не происходит взаимного перехода кинетической и потенциальной энергии частиц. Мгновенные значения той и другой энергии изменяются одновременно (в фазе) соответственно изменению смещения частиц.
Для мгновенного значения энергии (потенциальной и кинетической) одной частицы можно записать:

где S- смещение частицы, w- частота колебания частицы, A- амплитуда колебания частицы, V- скорость волнового процесса, в котором участвует частица, m – масса одной частицы.
Из формулы 18 следует, что мгновенные значения энергии каждой частицы среды изменяются во времени с удвоенной частотой колебания, причем в каждый момент времени эти значения для различных частиц отличаются. Однако среднее значение энергии за период колебания для всех частиц одинаково и составляет:
eср = 
Рассчитаем энергию волны для некоторого объема DV среды, в которой она распространяется.
Если в единице объема среды содержится N частиц, то r = Nm —плотность среды и среднее значение энергии волны в объеме DV будет:
Еср = 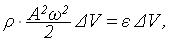
где 
Величина, численно равная средней энергии Еср, переносимой волной в единицу времени t через заданную поверхность S, перпендикулярную направлению распространения волны, называется потоком энергии через эту поверхность:
Ф = 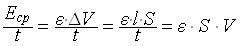
и измеряется в единицах мощности — Вт.
Поток энергии, приходящийся на единицу поверхности, называется плотностью потока энергии:
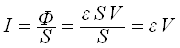
и измеряется в Вт/м2. Плотность потока энергии называют также интенсивностью волны.
В векторной форме:
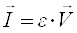
Плотность потока энергии, переносимого волной, можно рассматривать как вектор, совпадающий по направлению с вектором скорости волны.
Уровень интенсивности звука = 10 lg (J/J0) дБ
Поскольку звуки столь сильно различаются по интенсивности, удобнее рассматривать ее как логарифмическую величину и измерять в децибелах. Логарифмическая величина интенсивности представляет собой логарифм отношения рассматриваемого значения величины к ее значению, принимаемому за исходное. Уровень интенсивности J по отношению к некоторой условно выбранной интенсивности J0 равен
Таким образом, один звук, превышающий другой по уровню интенсивности на 20 дБ, превышает его в 100 раз по интенсивности.
В практике акустических измерений принято выражать интенсивность звука через соответствующую амплитуду избыточного давления Ре. Когда давление измеряется в децибелах относительно некоторого условно выбранного давления Р0, получают так называемый уровень звукового давления. Поскольку интенсивность звука пропорциональна величине Pe 2 , а lg(Pe 2 ) = 2lgPe, уровень звукового давления определяется следующим образом:
Уровень звукового давления = 20 lg (Pe/P0) дБ
Условное давление Р0 = 2Ч10 —5 Па соответствует стандартному порогу слышимости для звука с частотой 1 кГц.
Уровень громкости звука —относительная величина, которая выражается в фонах и численно равна уровню звукового давления (в децибелах — дБ), создаваемого синусоидальным тоном частотой 1 кГц такой же громкости, как и измеряемый звук (равногромким данному звуку).
3.6 Электромагнитная волна, условие и механизм ее возникновения. Скорость и длина электромагнитной волны в вакууме и в различных средах. Показатель преломления среды. Шкала электромагнитных волн. Характеристика электромагнитных волн различных интервалов длин волн.
Электромагнитные волны-это процесс распространения переменных магнитного и электрического полей. Переменное электрическое поле порождает магнитное, которое оказывается переменным. Оно порождает электрическое. Если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле, то в окружающем заряды пространстве возникнет последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке.
Скорость в вакууме: Е=М=1 V=C=3*10^8(м/с ) V=C/((E*M)^1/2),
Где E-диэлектрическая проницаемость среды, M-магнитная проницаемость среды.
Показатель преломления(абс.)- отношение скорости волны в вакууме к скорости в среде.
n=C/V =лямда(0)/лямда лямда(0)=С/ню лямда=V/ню
3.7 Интерференция когерентных волн. Амплитуда результирующего колебания при интерференции 2х волн, условия максимумов и минимумов амплитуды. Интерференционный спектр.
Интерференция- такое положение когерентных волн, при которой имеет место перераспределение энергии волн в пространстве и устойчивое во времени и пространстве усиление колебаний в одних местах и ослабление в других.
Когерентные волны- волны одинаковой частоты, разность фаз которых не зависит от времени.
Если источник света монохромотичный (одного цвета)-то на интерференционной картине полосы черные и цвета соответствуют источнику. Если источник излучает белый (сложный) свет, то интерференционная картина представляет собой чередующиеся спектры цветов (от фиолетового до красного)=> максимумы разлагаются в спектры.
3.8. Осуществление интерференции света с помощью тонкой пленки. Интерференционные полосы равной толщины и равного наклона.
Кольца Ньютона (пример полос равной толщины) При отражении от соприкосновения плоскопараллельной толстой стеклянной пластины и плосковыпуклой линзы с большим радиусом кривизны. Радиус темных колец в отраженном и светлых в проходящем : r=(nRh)^1/2
Где h(лямда)-длина волны,R- радиус кривизны линзы.
Радиус светлых колец в отраженном и темных в проходящем:r=((n-1/2)Rh)^1/2
3.9. Стоячая волна как частный случай интерференции. Уравнение плоской стоячей волны. Амплитуда, узлы и пучности стоячей волны. Превращения энергии в стоячей волне. Образование стоячей волны в сплошной ограниченной среде. Условия возникновения волны в стержне, в столбе воздуха, в натянутой струне. Стоячая волна в сплошной ограниченной среде как резонансное колебание.
3.10. Дифракция волн. Объяснение дифракции волн на основе принципа Гюйгенса-Френеля. Дифракция Фраунгофера на одной щели и на дифракционной решетке. Дифракционный спектр.
4.1 Тепловое Излучение, его энергетические характеристики. Закон Кирхгофа, Стефана-Больцмана, Вина. Постулат Планка.
Тепловое излучение — электромагнитное излучение, испускаемое нагретыми телами за счёт их тепловой энергии.
Примером теплового излучения является свет от лампы накаливания.
· Энергетическая светимость тела.
Энергетическая светимость тела- физическая величина, являющаяся функцией температуры и численно равная энергии, испускаемой телом в единицу времени с единицы площади поверхности по всем направлениям и по всему спектру частот.
Или (по лекции):
Это физическая величина, численно равная мощности излучения единицы поверхности нагретого тела по всему диапазону длин волн. 


· Спектральная плотность энергетической светимости.
Спектральная плотность энергетической светимости — функция частоты и температуры характеризующая распределение энергии излучения по всему спектру частот (или длин волн).
Или (по лекции):
Это физическая величина, численно равная энергии, излучаемой телом с единицы поверхности в единицу времени в единичном диапазоне длин волн.
· Поглощающая способность тела.
Поглощающая способность тела — функция частоты и температуры, показывающая, какая часть энергии электромагнитного излучения, падающего на тело, поглощается телом в области частот вблизи.
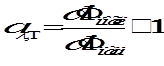
То, что не было в лекции:
· Отражающая способность тела.
Отражающая способность тела — функция частоты и температуры, показывающая какая часть энергии электромагнитного излучения, падающего на тело, отражается от него в области частот вблизи.
· Объемная плотность энергии излучения.
Объемная плотность энергии излучения — функция температуры, численно равная энергии электромагнитного излучения в единицу объема по всему спектру частот
· Спектральная плотность энергии.
Спектральная плотность энергии — функция частоты и температуры, связанная с объемной плотностью излучения формулой.
Закон излучения Кирхгофа — физический закон, установленный немецким физиком Кирхгофом в 1859 году. В современной формулировке закон звучит следующим образом:
Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы.
Или (по лекции):
Для всех тел, нагретых до одинаковой температуры, отношение спектральная плотности энергетической светимости 

Закон Стефана-Больцмана — закон излучения абсолютно чёрного тела. Определяет зависимость мощности излучения абсолютно чёрного тела от его температуры. Формулировка закона:
Мощность излучения абсолютно чёрного тела прямо пропорциональна четвёртой степени температуры тела.
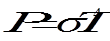

Закон смещения Вина даёт зависимость длины волны, на которой поток излучения энергии чёрного тела достигает своего максимума, от температуры чёрного тела.
Или (по лекции):


Постулат Планка:
Тела излучают энергию не непрерывно, а порциями. Энергия такой порции(кванта) равна:

4.2 Фотоэлектрический эффект. Вольт-амперная характеристика фототока. Опытные закономерности фотоэффекта. Уравнение Эйнштейна для фотоэффекта.
Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения).
Или (по лекции):
Явление вырывания электронов с поверхности металлов под действием света.
Вольт-амперная характеристика (ВАХ) — график зависимости тока от напряжения.
Опытные закономерности фотоэффекта или законы Столетова:
1) при неизменном спектральном составе электромагнитных излучений, падающих на фотокатод, фототок насыщения пропорционален энергетической освещенности катода.
Или по методичке :
Сила фототока насыщения Iн прямо пропорциональна световому потоку Ф – средней по времени энергии, подающей на поверхность катода за единицу времени.

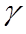

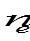
2) Максимальная начальная скорость фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой.
3) Для каждого вещества существует красная граница фотоэффекта, то есть минимальная частота ν0 света (зависящая от химической природы вещества и состояния поверхности), ниже которой фотоэффект невозможен.
Уравнение Эйнштейна для фотоэффекта.
Есть ещё много разновидностей этой формулы.
4.3 Фотоны. Корпускулярно-волновая природа света и частиц.
Фотон (от др. греч. φῶς, род. Пад. φωτός, «свет») — элементарная частица, квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать только двигаясь со скоростью света. Электрический заряд фотона также равен нулю.
Спин фотона равен 1 (частица является бозоном), но из-за нулевой массы покоя более подходящей характеристикой является спиральность, проекция спина частицы на направление движения. Фотон может находиться только в двух спиновых состояниях со спиральностью, равной . Этому свойству в классической электродинамике соответствует поперечность электромагнитной волны.
Корпускулярно-волновая природа света и частиц.
Корпускулярно-волновой дуализм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства.
4.4 Ядерная модель атома.
Первая попытка создания модели атома на основе накопленных экспериментальных данных (1903 г.) принадлежит Дж. Томсону. Он считал, что атом представляет собой электронейтральную систему шарообразной формы радиусом, примерно равным 10–10 м. Положительный заряд атома равномерно распределен по всему объему шара, а отрицательно заряженные электроны находятся внутри него. Для объяснения линейчатых спектров испускания атомов Томсон пытался определить расположение электронов в атоме и рассчитать частоты их колебаний около положений равновесия. Однако эти попытки не увенчались успехом. Через несколько лет в опытах великого английского физика Э. Резерфорда было доказано, что модель Томсона неверна.
Первые прямые эксперименты по исследованию внутренней структуры атомов были выполнены Э. Резерфордом и его сотрудниками Э. Марсденом и Х. Гейгером в 1909–1911 годах. Резерфорд предложил применить зондирование атома с помощью α-частиц. От радиоактивного источника, заключенного в свинцовый контейнер, α-частицы направлялись на тонкую металлическую фольгу. Рассеянные частицы попадали на экран, покрытый слоем кристаллов сульфида цинка, способных светиться под ударами быстрых заряженных частиц. Сцинтилляции (вспышки) на экране наблюдались глазом с помощью микроскопа. Наблюдения рассеянных α-частиц в опыте Резерфорда можно было проводить под различными углами φ к первоначальному направлению пучка. Было обнаружено, что большинство α-частиц проходит через тонкий слой металла, практически не испытывая отклонения. Однако небольшая часть частиц отклоняется на значительные углы, превышающие 30°. Очень редкие α-частицы (приблизительно одна на десять тысяч) испытывали отклонение на углы, близкие к 180°.
Этот результат был совершенно неожиданным даже для Резерфорда. Его представления находил в резком противоречии с моделью атома Томсона, согласно которой положительный заряд распределен по всему объему атома. При таком распределении положительный заряд не может создать сильное электрическое поле, способное отбросить α-частицы назад. Электрическое поле однородного заряженного шара максимально на его поверхности и убывает до нуля по мере приближения к центру шара. Если бы радиус шара, в котором сосредоточен весь положительный заряд атома, уменьшился в n раз, то максимальная сила отталкивания, действующая на α-частицу, по закону Кулона возросла бы в n2 раз. Следовательно, при достаточно большом значении n α-частицы могли бы испытать рассеяние на большие углы вплоть до 180°. Эти соображения привели Резерфорда к выводу, что атом почти пустой, и весь его положительный заряд сосредоточен в малом объеме. Эту часть атома Резерфорд назвал атомным ядром. Так возникла ядерная модель атома.
Радикальные выводы о строении атома, следовавшие из опытов Резерфорда, заставляли многих ученых сомневаться в их справедливости. Опираясь на классические представления о движении микрочастиц, Резерфорд предложил планетарную модель атома. Согласно этой модели, в центре атома располагается положительно заряженное ядро, в котором сосредоточена почти вся масса атома. Атом в целом нейтрален. Вокруг ядра, подобно планетам, под действием кулоновских сил со стороны ядра вращаются электроны. Находиться в состоянии покоя электроны не могут, так как они упали бы на ядро.
Планетарная модель атома, предложенная Резерфордом, несомненно явилась крупным шагом вперед в развитии знаний о строении атома. Она была совершенно необходимой для объяснения опытов по рассеянию α-частиц, однако оказалась неспособной объяснить сам факт длительного существования атома, т. е. его устойчивость. По законам классической электродинамики, движущийся с ускорением заряд должен излучать электромагнитные волны, уносящие энергию. За короткое время (порядка 10 –8 с) все электроны в атоме Резерфорда должны растратить всю свою энергию и упасть на ядро. То, что этого не происходит в устойчивых состояниях атома, показывает, что внутренние процессы в атоме не подчиняются классическим законам.
4.5 Состав ядер атомов. Радиоактивность ядер. Реакции деления и синтез ядер.
Состав ядер атомов.
Физики Д. Д. Иваненко и В. Гейзенберг в 1932 г. выдвинули протонно-нейтронную модель атомного ядра. Согласно этой модели, ядро атома любого вещества состоит из протонов и нейтронов. (Общее название протонов и нейтронов — нуклоны.) Число протонов равно заряду ядра и совпадает с номером элемента в таблице Менделеева. Сумма числа протонов и нейтронов равна массовому числу.
Химические вещества, занимающие одно и то же место в таблице Менделеева, но имеющие разную атомную массу, называются изотопами. Ядра изотопов отличаются числом нейтронов. Например, водород имеет три изотопа: протии — ядро состоит из одного протона, дейтерий — ядро состоит из одного протона и одного нейтрона, тритий — ядро состоит из одного протона и двух нейтронов.
Лишь небольшая часть нуклидов являются стабильными. В большинстве случаев ядерные силы оказываются неспособны обеспечить их постоянную целостность, и ядра рано или поздно распадаются. Это явление получило название радиоактивности.
Установлено, что радиоактивны все химические элементы с порядковым номером, большим 82.
α-распадом называют самопроизвольный распад атомного ядра на дочернее ядро и α-частицу (ядро атома 4 He).
β-распад (точнее, бета-минус-распад, -распад) — это радиоактивный распад, сопровождающийся испусканием из ядра электрона и антинейтрино.
β-распад является внутринуклонным процессом. Он происходит вследствие превращения одного из d-кварков в одном из нейтронов ядра в u-кварк; при этом происходит превращение нейтрона в протон с испусканием электрона и антинейтрино:
Термин «гамма-распад» применяется редко; испускание ядром гамма-квантов называют обычно изомерным переходом. Гамма-излучение часто сопровождает другие типы распада.
Реакции деления и синтез ядер.
Деление представляет собой распад (расщепление) атомного ядра на две приближённо равные части (осколки), сопровождающийся выделением энергии и, в отд. случаях, испусканием одной или нескольких частиц, например, нейтронов. Некоторые тяжелые ядра могут делиться самопроизвольно (спонтанно), более легкие — в случае соударения с другими ядрами, обладающими большой энергией. Кроме того, тяжелые ядра, например, атомов урана, способны делиться под воздействием бомбардировки нейтронами, а поскольку при этом испускаются новые нейтроны, процесс может стать самоподдерживающимся, т.е. возникает цепная реакция. В ходе такой реакции деления происходит высвобождение большого количества энергии. Синтезом называется слияние ядер двух легких атомов с образованием нового ядра, соответствующего более тяжелому атому. Если это новое ядро стабильно, то при синтезе выделяется энергия, поскольку связи в нем оказываются более прочными, чем в исходных ядрах. От химических реакций ядерный синтез отличается участием в нем не только электронов атомов, но и их ядер. энергии, чем в реакциях деления. Синтез ядер идет в центр, области Солнца и других звезд, являясь источником их энергии.
4.6 Элементарные и фундаментальные частицы. Обменный механизм взаимодействия.
Элементарная частица — собирательный термин, относящийся к микрообъектам в субъядерном масштабе, которые невозможно расщепить на составные части.
Следует иметь в виду, что некоторые элементарные частицы (электрон, фотон, кварки и т. д.) на данный момент считаются бесструктурными и рассматриваются как первичные фундаментальные частицы.
Строение и поведение элементарных частиц изучается физикой элементарных частиц.
Все элементарные частицы делятся на два класса:
· бозоны — частицы с целым спином (например, фотон, глюон, мезоны).
· фермионы — частицы с полуцелым спином (например, электрон, протон, нейтрон, нейтрино).
- Техническая акустика и защита от шума. Лекция №2 Уравнение плоской синусоидальной волны.
- Описание презентации по отдельным слайдам:
- Дистанционное обучение как современный формат преподавания
- Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Уравнение плоской синусоидальной волны амплитуда ускорения
- 🔥 Видео
Видео:10й класс; Физика; "Уравнение плоской волны"Скачать

Техническая акустика и защита от шума. Лекция №2 Уравнение плоской синусоидальной волны.
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
Техническая акустика и защита от шума
Лекция №2
Уравнение плоской синусоидальной волны. Волновое число.
Уравнение сферической волны
Диапазоны частот акустических волн.
Понятия шума, основного тона, обертона, тембра музыкальных звуков.
Громкость звука, порог слышимости, порог осязания.
Уровень интенсивности акустических волн. Ультразвук.
! ! ! Волна называется плоской, если ее волновые повеpхности пpедставляют собой паpаллельные дpуг дpугу плоскости, пеpпендикуляpные фазовой скоpости волны
6 Уравнение плоской синусоидальной волны. Волновое число
S зависит не только от времени, но и от
координаты.
v — скорость распространения волны, А — амплитуда волны, аргумент синуса — фаза волны, 𝜑 0 — начальная фаза колебаний в точке х = 0, 𝜔 — частота (циклическая) волны.
Уравнение имеет вид:
Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется ДЛИНОЙ ВОЛНЫ 𝜆=𝜈𝑇.
Введем ВОЛНОВОЕ ЧИСЛО k, равное:
𝑘= 2𝜋 𝜆
Тогда уравнение плоской волны примет вид:
𝑆=𝐴∙sin 𝜔𝑡−𝑘𝑥+ 𝜑 0
http://koi.tspu.ru/waves/ch4_2.htm
При записи уравнения сферической волны учитывается, что амплитуда волны убывает с расстоянием от источника:
𝑆= 𝐴 0 𝑟 sin(𝜔𝑡− 𝑘∙𝑟 + 𝜑 0 )
𝑘 − ВОЛНОВОЙ ВЕКТОР, модуль которого 𝑘 равен волновому числу, а направление совпадает с направлением луча распространения волны.
7 Уравнение сферической волны
http://edu.dvgups.ru/METDOC/ENF/PHIZIK/PHIZIK/LAB_RAB/SKOROST_ZVUKA/MAIN.HTM
Инфразвуковой — ниже 20 Гц.
Звуковой — от 20 Гц до 20 кГц (в него полностью укладывается диапазон средне статистических людей слышимых человеческим ухом частот). Более 20 кГц человеческое ухо может услышать диапазон. Изначально с рождения ребёнок слышит ультразвук с частотой более 20 кГц, но после в возрастом происходит уплотнение стен перепонок.
Ультразвуковой — от 20 кГц до 100кГц.
Гиперзвуковой — свыше 100кГц.
8 Диапазоны частот акустических волн
Шкала диапазона частот
Шум — беспорядочные колебания различной физической природы, отличающиеся сложностью временной спектральной структуры.
Шум – одновременное сочетание звуков различной частоты.
9 Понятия шума, основного тона, обертона, тембра музыкальных звуков.
Чистый тон — это звук , совершающий гармонические колебания одинаковой частоты.
Звуки разных источников (например разные музыкальные инструменты, человеческий голос, звуки посторонних предметов и т.д ) вместе составляют совокупность гармонических колебаний разных частот.
Основной частотой называется самая маленькая частота этого многосоставного звука, а звук который ей соответствует и он определенной высоты называется основным тоном.
ОБЕРТОН (от нем. Oberton — высокий тон, высокий звук) — синусоидальная составляющая звуковых колебаний сложной формы с частотой, более высокой, чем основной тон.
Любое периодическое колебание можно представить как сумму основного тона и обертонов, причём частоты и амплитуды этих обертонов определяются как физическими свойствами колебательной системы, так и способом её возбуждения.
Если частоты всех обертонов — целые кратные основной частоте, то такие обертоны называют гармоническими или гармониками. Если же частоты зависят от основной частоты более сложным образом, то говорят о негармонических обертонах. В этом случае представление периодических колебания в виде суммы гармоник будет приближённым, но тем более точным, чем большее число гармоник взято.
Если частота основного тона f (первая гармоника), то частота второй гармоники равна 2f или близка к этому значению, частота третьей 3f и т. д. Состав и количество обертонов сложного звука определяет его качественную окраску, или тембр звука.
Те́мбр (фр. timbre — «колокольчик», «метка», «отличительный знак») — колористическая (обертоновая) окраска звука; одна из специфических характеристик музыкального звука (наряду с его высотой, громкостью и длительностью).
По тембрам отличают звуки одинаковой высоты и громкости, но исполненные на различных инструментах, разными голосами, или же на одном инструменте, но разными способами, штрихами и т. п.
При восприятии тембров обычно возникают различные ассоциации: тембральную специфику звука сравнивают с органолептическими ощущениями от тех или иных предметов и явлений, например, звуки называют яркими, блестящими, матовыми,тёплыми, холодными, глубокими, полными, резкими, насыщенными, сочными, металлическими, стеклянными; применяются и собственно слуховые определения (например, звонкие, глухие, шумные).
Человек номинально слышит звуки в диапазоне от 16 до 20 000 Гц.
Диапазон громкости воспринимаемых звуков огромен. Но барабанная перепонка в ухе чувствительна только к изменению давления. Уровень давления звука принято измерять в децибелах (дБ).
10 Громкость звука, порог слышимости, порог осязания
Нижний порог слышимости определён как 0 дБ (20 микропаскаль) 20∙10-5 Па, а определение верхнего предела слышимости относится скорее к порогу дискомфорта и далее — к нарушению слуха, контузии и т. д. Этот предел зависит от того, как долго по времени мы слушаем звук. Ухо способно переносить кратковременное повышение громкости до 120 дБ без последствий, но долговременное восприятие звуков громкостью более 80 дБ может вызвать потерю слуха.
Минимальный порог, при котором звук остаётся слышен, зависит от частоты. График этой зависимости получил название абсолютный порог слышимости. В среднем, он имеет участок наибольшей чувствительности в диапазоне от 1 кГц до 5 кГц, хотя с возрастом чувствительность понижается в диапазоне выше 2 кГц.
Человеческий слух во многом подобен спектральному анализатору, то есть ухо распознаёт спектральный состав звуковых волн без анализа фазы волны. В реальности фазовая информация распознаётся и очень важна для направленного восприятия звука, но эту функцию выполняют ответственные за обработку звука отделы головного мозга.
Разница между фазами звуковых волн, приходящих на правое и левое ухо, позволяет определять направление на источник звука, причём информация о разности фаз имеет первостепенное значение, в отличие от изменения громкости звука воспринимаемого разными ушами.
Порогом осязания ( порогом болевого ощущения) называется наибольшая интенсивность звуковой волны, при которой восприятие звука не вызывает болевого ощущения. Порог осязания зависит от частоты звука, изменяясь от 0,1 Вт/м2 при 6000 Гц до 10 Вт/м2 при низких и высоких частотах.
Интенсивность звука — скалярная физическая величина, характеризующая мощность, переносимую звуковой волной в направлении распространения. Количественно интенсивность звука равна среднему по времени потоку звуковой энергии через единичную площадку, расположенную перпендикулярно направлению распространения звука:
𝐼= 1 𝑇 𝑡 𝑡+𝑇 𝑑𝑃 𝑑𝑆 𝑑𝑡
11. Уровень интенсивности акустических волн, интенсивность. Ультразвук
Звуки способны сильно различаются по интенсивности, потому удобнее рассматривать интенсивность как логарифмическую величину и измерять в децибелах (дБ). Логарифмическая величина интенсивности представляет собой логарифм отношения рассматриваемого значения величины к ее значению, принимаемому за исходное.
Уровень интенсивности I по отношению к некоторой условно выбранной интенсивности I0 равен:
𝛽=10𝑙𝑔 𝐼 𝐼 0 , дБ
Таким образом, один звук, превышающий другой по уровню интенсивности на 20 дБ, превышает его в 100 раз по интенсивности.
Ультразву́к — упругие колебания в среде с частотой за пределом слышимости человека. Обычно под ультразвуком понимают частоты выше 20 000 Гц.
Частота ультразвуковых колебаний, применяемых в промышленности и биологии, лежит в диапазоне от нескольких десятков КГц до единиц МГц. Высокочастотные колебания обычно создают с помощью пьезокерамических преобразователей, например, из титанита бария. В тех случаях, когда основное значение имеет мощность ультразвуковых колебаний, обычно используются механические источники ультразвука. Первоначально все ультразвуковые волны получали механическим путем (камертоны, свистки, сирены).
В природе УЗ встречается как в качестве компонентов многих естественных шумов (в шуме ветра, водопада, дождя, в шуме гальки, перекатываемой морским прибоем, в звуках, сопровождающих грозовые разряды, и т. д.), так и среди звуков животного мира. Некоторые животные пользуются ультразвуковыми волнами для обнаружения препятствий, ориентировки в пространстве и общения (киты, дельфины, летучие мыши, грызуны).
В медицине (УЗИ)
Применение ультразвука в косметологии
Резка и сварка металла
Приготовление гомогенных смесей
В биологии
Чистка в промышленности и быту
Применение ультразвука в эхолокации
Применение ультразвука в расходометрии
В дефектоскопии
В гальванотехнике
Свисто́к Га́льтона — акустический излучатель, работающий по принципу свистка (рассечение воздушного потока клином, расположенным рядом с акустическим резонатором). Первое изобретенное устройство для получения ультразвука.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 939 человек из 80 регионов
Курс повышения квалификации
Инструменты онлайн-обучения на примере программ Zoom, Skype, Microsoft Teams, Bandicam
- Курс добавлен 31.01.2022
- Сейчас обучается 23 человека из 14 регионов
Курс повышения квалификации
Педагогическая деятельность в контексте профессионального стандарта педагога и ФГОС
- Сейчас обучается 40 человек из 24 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Получение уравнения плоской бегущей волны.Скачать

Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 587 541 материал в базе
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 29.12.2020
- 86
- 3
- 29.12.2020
- 77
- 0
- 29.12.2020
- 83
- 0
- 29.12.2020
- 95
- 1
- 29.12.2020
- 98
- 3
- 29.12.2020
- 91
- 0
- 29.12.2020
- 147
- 1
- 29.12.2020
- 205
- 7
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 09.12.2020 255
- PPTX 1018.8 кбайт
- 0 скачиваний
- Оцените материал:
Настоящий материал опубликован пользователем Паршина Кира Максимовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 1 год и 1 месяц
- Подписчики: 0
- Всего просмотров: 24480
- Всего материалов: 230
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Забайкалье в 2022 году обеспечат интернетом 83 школы
Время чтения: 1 минута
В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
Инфоурок стал резидентом Сколково
Время чтения: 2 минуты
Ленобласть распределит в школы прибывающих из Донбасса детей
Время чтения: 1 минута
В школах Хабаровского края введут уроки спортивной борьбы
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Только 23 февраля!
Получите новую
специальность
по низкой цене
Цена от 1220 740 руб. Промокод на скидку Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки
Видео:Амплитуда, период, частота и длина волны периодических волнСкачать

Уравнение плоской синусоидальной волны амплитуда ускорения
4.1. Механические колебания.
4.2. Электрические колебания.
4.3. Упругие волны. Акустика.
4.4. Электромагнитные волны. Излучение.
_______________________________________________________________________________________________
4.1. Механические колебания.
4.1.1. Гармонические колебания.
4.1. 1 -1. Частица совершает гармоническое колебание с амплитудой А и периодом Т = 12 с. Найти время t ₁ , за которое смещение частицы изменяется от 0 до А/2.
Решение:
Т = 12 с
х(0) = 0
х( t ₁) = А/2 (1)
t ₁ – ?
Так как начальное положение частицы х(0) = 0, то частица колеблется по закону синуса с начальной фазой ϕ ₀ = 0:
x = Asin ( ωt + ϕ ₀) или
x = Asinωt , (2)
где ω = 2 π / T – круговая частота.
С учётом условия (1), запишем (2) в виде:
х( t ₁) = Asin ( ωt ₁); А/2 = Asin ( (2 π / T ) t ₁ ); 1/2 = sin (2 πt ₁/ T ); 2 πt ₁/ T = π /6. Отсюда
t ₁ = T /12.
t₁ = 12/12 = 1 с.
Ответ: t₁ = T/12 = 1 c.
4.1.1-2. Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.
где − I момент инерции диска относительно оси вращения, проходящей через точку подвеса А (см. рис.); x = AO = R − расстояние от точки подвеса до центра тяжести О диска; m − масса диска; g = 9,8 м/с² − ускорение свободного падения.
Момент инерции I ₀ диска относительно оси симметрии диска:
I ₀ = mR ²/2.
По теореме Штейнера:
I = I₀ + mR². Имеем
I = mR²/2 + mR² = 3mR²/2. Тогда по (1)
Решение:
r ( t ) = A ( icosωt + jsinωt ) (1)
A = 0,5 м
ω = 5 с⁻¹
v − ?
an − ?
Представим (1) в виде:
r ( t ) = iAcosωt + jAsinωt (1*)
Радиус вектор r ( t ) точки: r ( t ) = ix + jy , где x , y − проекции радиус вектора соответственно на оси OX и OY ; i , j − единичные векторы (орты), направленные соответственно по оси OX и OY . Тогда (1*) примет вид
ix + jy = iAcosωt + jAsinωt ,
отсюда получим два уравнения
x = Acosωt , (*)
y = Asinωt . (**)
Возведём их в квадрат
x ² = A ² cos ² ωt ,
y ² = A ² sin ² ωt .
Сложим эти уравнения
x ² + y ² = A ² cos ² ωt + A ² sin ² ωt или x ² + y ² = A ²( cos ² ωt + sin ² ωt ). Отсюда, т.к. cos ² ωt + sin ² ωt = 1, получим уравнение траектории движения точки
x ² + y ² = A ². (2)
Уравнение (2) − это уравнение окружности радиусом R = A = 0,5 м с центром в начале координат (см. рис.).
Найдём проекции скорости v x и vy . Для этого продифференцируем x и y из (*) и (**) по времени t :
vx = xt ʹ = ( Acosωt ) t ʹ = — Aωsinωt ;
vy = yt ʹ = ( Asinωt ) t ʹ = Aωcosωt .
Тогда квадрат скорости
v ² = vx ² + vy ² или v ² = (- Aωsinωt )² + ( Aωcosωt )² или v ² = A ² ω ²( sin ² ωt + cos ² ωt ) или v ² = A ² ω ². Отсюда модуль скорости v :
v = Aω . (3)
v = 0,5·5 = 2,5 м/с².
Модуль нормального ускорения an : an = v ²/ R или, с учётом (3) и R = A , получим an = A ² ω ²/ A или
an = Aω ².
an = 0,5·5² = 12,5 м/с².
Ответ: траектория − окружность радиусом R = A = 0,5 м с центром в начале координат, v = Aω = 2,5 м/с², an = Aω ² = 12,5 м/с².
_______________________________________________________________________________________________
4.1.2. Свободные затухающие колебания.
4.1.2-1. Амплитуда затухающих колебаний уменьшилась в n = 100 за 15 с. Чему равен коэффициент затухания β ?
Решение:
t = 15 c
n = 100
A = A ₀/ n (*)
β – ?
Зависимость амплитуды А затухающих колебаний от времени t :
A = A ₀ e — β t , (1)
где A ₀ – начальная амплитуда; β – коэффициент затухания.
Имеем из (1) и (*):
A ₀/ n = A ₀ e — β t ; 1/ n = e — β t ; e β t = n ; βt = ln ( n ) отсюда
β = ln ( n )/ t .
β = ln(100)/15 = 0,307 1/c.
Ответ: β = ln(n)/t = 0,307 1/c.
4.1.2-2. Найти логарифмический декремент затухания тонкого стержня, подвешенного за один из его концов, если за промежуток времени t = 5 мин его полная механическая энергия уменьшилась в n = 4 · 10 ² раз. Длина стержня L = 50 см.
Решение:
t = 5 мин = 300 с
n = 400
L = 0,5 м
λ − ?
В данном случае стержень − это физический маятник.
Логарифмический декремент затухания λ
λ = βT , (1)
где β – коэффициент затухания, T − период колебаний стержня.
1. Найдём коэффициент затухания β .
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
ω – частота затухающих колебаний; ω ₀ – собственная частота колебаний.
Зависимость от времени t полной механической энергии Е физического маятника:
Е = E ₀ e -2 βt ,
где E ₀ – начальная (при t = 0) полная механическая энергия.
Отсюда имеем
n = Е ₀/ Е = Е ₀/( E ₀ e -2 βt ) = 1 /( e -2 βt ) = e 2 βt .
Получили n = e 2 βt . Прологарифмируем это равенство Ln ( n ) = 2 βt . Отсюда
β = Ln ( n )/(2 t ). (3)
2. Найдём период Т затухающих колебаний.
Оценим коэффициент β 2 по (3).
β = Ln (400)/(2 · 300) = 0,009986, отсюда
β ² = (0,009986)² ≈ 0,0000997.
Собственная частота колебаний физического маятника:
Подставим в (1) найденные β из (3) и Т из (4**) и, после упрощения, получим
4.1.2-3. Логарифмический декремент затухания тела, колеблющегося с частотой 50 Гц, равен 0,02. Определите: время, за которое амплитуда колебаний тела уменьшится в 20 раз; число колебаний тела, чтобы произошло подобное уменьшение амплитуды.
Решение:
ν = 50 Гц
λ = 0,02
n = 20
t − ?
N − ?
1. Пусть β – коэффициент затухания; T = 1/ ν – период, ν – частота колебаний. Логарифмический декремент затухания λ :
λ = βT или λ = β / ν , отсюда
β = λν . (1)
Амплитуда А затухающих колебаний
A = A ₀· e — βt ,
где A ₀ − начальная амплитуда (при t = 0).
Подставим сюда из условия задачи A = A ₀/ n :
A ₀/ n = A ₀· e — βt ,
отсюда e βt = n и, после логарифмирования, βt = Ln ( n ), отсюда
t = ( Ln ( n ) )/ β и, с учётом (1),
t = ( Ln ( n ) )/( λν ). (2)
2. Число колебаний N за время t :
N = t / T = tν = ( и, с учётом (2), ) = ν ( Ln ( n ) )/( λν ) или
N = ( Ln ( n ) )/ λ . (3)
3. Вычисления по формулам (2) и (3):
t = ( Ln (20) )/(0,02·50) ≈ 3 с.
N = ( Ln (20) )/0,02 ≈ 150.
Ответ: t = ( Ln ( n ) )/( λν ) ≈ 3 с; N = ( Ln ( n ) )/ λ ≈ 150.
4.1.2-4. Составьте дифференциальное уравнение гармонических свободных затухающих крутильных колебаний механической системы.
Решение:
Пусть система (например, тонкий однородный диск, подвешенный в горизонтальном положении к упругой нити) совершает крутильные колебания относительно закреплённой оси Z (ось нити). Пусть на диск действует упругая сила, проекция момента которой на ось Z равна
Mz = — kϕ , (1)
где k − постоянная, ϕ − угол поворота из положения равновесия. Знак “минус” указывает на то, что при отклонении системы на угол ϕ , момент упругой силы возвращает систему к положению равновесия. Поместим диск в вязкую среду ( например, жидкость ). Момент силы сопротивления Mc , действующий на диск, пропорционален угловой скорости ϕ ʹ:
M c = — ηϕ ʹ, (2)
где η − постоянная.
Уравнение динамики вращательного движения диска имеет вид
Iϕ ʹʹ = Mz + M c , (3)
где I – момент инерции диска относительно оси вращения.
С учётом (1) и (2), уравнение (3) примет вид Iϕ ʹʹ = — kϕ — ηϕ ʹ, отсюда
ϕ ʹʹ + ( η / I ) ϕ ʹ + ( k / I ) ϕ = 0.
Применив обозначения 2 β = η / I , ω ₀² = k / I , перепишем последнее уравнение:
ϕ ʹʹ + 2 βϕ ʹ + ω ₀² ϕ = 0.
Это дифференциальное уравнение описывает затухающие крутильные колебания механической системы.
Ответ: ϕ ʹʹ + 2 βϕ ʹ + ω ₀² ϕ = 0.
4.1.2-5. Найти добротность Q осциллятора, у которого отношение резонансной частоты ωрез к частоте затухающих колебаний ω равно η.
Решение:
ωрез/ω = η (*)
Q − ?
Пусть β − коэффициент затухания, ω₀ − собственная частота колебаний, T = 2π/ω − период затухающих колебаний, λ = βT = 2πβ/ω − логарифмический декремент затухания. Тогда добротность Q:
Q = π/λ = π/(2πβ/ω), или
Q = ω/(2β). (1)
Связь частот ω и ω₀:
ω² = ω₀² — β². (2)
Формула для резонансной частоты ωрез:
ωрез² = ω₀² — 2β². (3)
Из (2) вычтем (3)
ω² — ωрез² = (ω₀² — β²) — (ω₀² — 2β²), или
ω² — ωрез² = ω₀² — β² — ω₀² + 2β², или
ω² — ωрез² = β². (**)
С учётом условия (*) имеем ωрез = ωη. Тогда (**) примет вид
ω² — ω²η² = β², или
ω²(1 — η²) = β², отсюда
___________________________________________________________________________________
4.1.3. Вынужденные колебания. Резонанс.
4.1.3-1. Осциллятор массы m движется по закону x = Asinωt под действием вынуждающей силы Fₓ = F₀cosωt. Найти коэффициент затухания β осциллятора.
Решение:
m,
x = Asinωt,
Fₓ = F₀cosωt,
β − ?
Установившееся смещение х(t) осциллятора при вынужденных колебаниях:
x = Acos(ωt — ϕ), (1)
ω₀ − собственная частота колебаний осциллятора,
f₀ = F₀/m. (*)
Так как по условию смещение х(t) осциллятора x = Asinωt, то из (1) следует: ϕ = π/2
(т. к. cos(ωt — π/2) = sinωt). Тогда из (3) имеем:
где f₀ = F ₀/ m , m − масса осциллятора , β − коэффициент затухания, ω₀ − собственная частота колебаний, ω − частота вынужденных колебаний.
При постоянной амплитуде вынуждающей силы F ₀ (и, следовательно, постоянной f ₀) из (*) при двух разных частотах ω₁ и ω₂ получаем две амплитуды А₁ и А₂ вынужденных колебаний:
4.2. Электрические колебания.
4.2-1. Небольшая магнитная стрелка совершает малые колебания вокруг оси, перпендикулярной направлению внешнего магнитного поля. При изменении индукции этого поля период колебаний стрелки уменьшился в η = 5 раз. Во сколько раз и как изменилась индукция поля? Затухание колебаний пренебрежимо мало.
Решение:
T ₁/ T ₂ = η = 5
B ₂/ B ₁ − ?
Момент сил М, действующий на стрелку со стороны магнитного поля
М = [ B · P m ], где P m − вектор магнитного момента стрелки.
Модуль момента сил
М = B · P m · sinϕ , где ϕ – угол между векторами B и P m .
При малых колебаниях угол ϕ очень мал и sinϕ ≈ ϕ . Тогда
М = B · P m · ϕ .
При повороте стрелки на угол ϕ возникает момент сил М , стремящийся вернуть стрелку в положение равновесия, т.е. М = — B · P m · ϕ . Если J – момент инерции стрелки относительно оси вращения, то основное уравнение динамики вращательного движения примет вид
Jϕ ’’ = M или Jϕ ’’ = — B · P m · ϕ отсюда
ϕ ’’ + ( B · P m / J ) · ϕ = 0. (1)
Если ω – циклическая частота колебаний, то сравнивая (1) с уравнением гармонических колебаний
ϕ ’’ + ω ² ϕ = 0, получим
ω ² = B · P m / J , отсюда
ω = √( B · P m / J ).
Тогда период T колебаний
T = 2 π / ω или
T = 2 π √( J /( B · P m ) ). (2)
На основе (2) для разных B ₁ и B ₂ получим соответствующие T ₁ и T ₂
T ₁ = 2 π √( J /( B ₁ · P m ) )
T ₂ = 2 π √( J /( B ₂ · P m ) ).
Отсюда
T ₁/ T ₂ = √( B ₂/ B ₁) и отсюда
B ₂/ B ₁ = ( T ₁/ T ₂)² = η ² = 25. Итак
B ₂/ B ₁ = η ² = 25.
Ответ: индукция магнитного поля увеличится в η ² = 25 раз.
4.2-2. Индуктивность катушки равна 0,125 Гн. Уравнение колебаний силы ток в ней имеет вид:
i = 0,4 cos (1000 t ), где все величины выражены в системе СИ. Определить амплитуду напряжения на катушке.
Решение:
L = 0,125 Гн
i = 0,4 cos (1000 t ). (1)
Um − ?
Уравнение колебаний силы тока в катушке имеет вид:
i = Imcos ( ωt ). (2)
Из (1) и (2) имеем
Im = 0,4 А − амплитуда силы тока в катушке; ω = 1000 с⁻¹− частота.
Индуктивное сопротивление катушки: X L = ωL .
По закону Ома
Im = Um / X L , отсюда
Um = X L · Im или
Um = ωL · Im .
Um = 1000·0,125·0,4 = 50 В.
Ответ: Um = 50 В.
4.2-3. Электрический колебательный контур состоял из последовательно соединенных катушки с индуктивностью L = 0,8 Гн и конденсатора емкостью С. Сопротивление катушки и соединительных проводов было равно R = 2000 Ом. После того, как часть витков в катушке замкнулась накоротко, индуктивность ее уменьшилась в n = 7 раз, частота собственных колебаний в контуре возросла в k = 3 раза, а коэффициент затухания этих колебаний не изменился. Определить емкость конденсатора .
Решение:
L = 0,8 Гн
R = 2000 Ом
L ₂ = L / n
n = 7
ω ₂ = kω
k = 3
β = const
C − ?
Коэффициент затуханий β = R /(2 L ).
ω и ω ₂ − начальная и конечная частоты собственных колебаний в контуре, где
ω = √( 1/( LC ) — β ² ) = √( 1/( LC ) — R ²/(4 L ²) );
ω ₂ = √( 1/( L ₂ C ) — β ² ) = √( n /( LC ) — R ²/(4 L ²) ).
Возведём в квадрат равенство ω ₂ = kω , получим ω ₂² = k ² ω ² или
n /( LC ) — R ²/(4 L ²) = k ²( 1/( LC ) — R ²/(4 L ²) ), отсюда
C = 4 L ( k ² — n )/( R ²( k ² — 1) ).
C = 4·0,8·(3² — 7)/( 2000²·(3² — 1) ) = 2·10⁻⁷ Ф.
Ответ: C = 4L(k² — n)/( R²(k² — 1) ) = 2·10⁻⁷ Ф.
4.2-4. Ток в колебательном контуре зависит от времени как I = Imsinω₀t, где Im = 9,0 мА, ω₀ = 4,5·10⁴ с⁻¹. Ёмкость конденсатора С = 0,50 мкФ. Найти индуктивность контура и напряжение на конденсаторе в момент t = 0.
Решение:
I = Imsinω₀t (*)
Im = 9·10⁻³ А
ω₀ = 4,5·10⁴ с⁻¹
С = 0,5·10⁻⁶ Ф
L − ?
U(0) − ?
1). Собственная частота ω₀ колебательного контура
1
L = ––––– . (1)
ω₀²C
2). Закон сохранения энергии в колебательном контуре:
LI²/2 + CU²/2 = LIm²/2
или, с учётом (*),
L(Imsinω₀t)²/2 + CU²/2 = LIm²/2.
Отсюда при t = 0 (т.к. sinω₀0 = 0) получим напряжение U(0) = Um на конденсаторе в момент времени t = 0 ( Um − максимальное напряжение ):
CU²(0) = LIm²
и, подставляя сюда L из (1), получим
Im²
CU²(0) = ––––– или
ω₀²C
Im
U(0) = Um = –––– . (2)
ω₀C
Вычисления по формулам (1) и (2 ):
1
L = –––––––––––––––– = 0,001 Гн = 1 мГн.
(4,5·10⁴)²·0,5·10⁻⁶
9·10⁻³
U(0) = Um = –––––––––––––– = 0,4 В.
4,5·10⁴·0,5·10⁻⁶
4.3. Упругие волны. Акустика.
4.3-1. По шнуру слева направо бежит со скоростью v незатухающая гармоническая волна. При этом поперечное смещение точки О шнура изменяется по закону y = Acos ( ωt ). Как зависит от времени смещение точки шнура, находящейся правее точки О на расстоянии x от нее?
Решение:
y = Acos ( ω ( t — x / v ) ).
Ответ: y = Acos ( ω ( t – x / v ) ).
4.3-2. Уравнение плоской звуковой волны имеет вид ξ = 60 cos (1800 t — 5,3 x ). где ξ – в мкм, t – в секундах, х – в метрах .
Найти:
а) отношение амплитуды смещения частиц среды к длине волны;
б) амплитуду колебаний скорости частиц среды и ее отношение к скорости распространения волны;
в) амплитуду колебаний относительной деформации среды и её связь с амплитудой колебаний скорости частиц среды.
а) Уравнение плоской синусоидальной волны
ξ = Acos(ωt – kx). (2)
Из (1) и (2) следует
A = 60 ·10 ⁻ ⁶ м – амплитуда колебаний частиц среды,
ω = 1800 1/с – циклическая частота,
k = 5,3 1/м – волновое число.
k = 2π/λ, отсюда λ = 2π/k. Тогда
A/λ = A/(2π/k) или
A/λ = Ak/(2π).
A / λ = 60 ·10 ⁻ ⁶ · 5,3/(2 · 3,14) = 5,1 ·10 ⁻ ⁵ .
б) Амплитуда колебаний скорости частиц среды
V m = Aω . (*)
Vm = 60 ·10 ⁻ ⁶ · 1800 = 0,11 м/с. = 11 см/с.
Скорость распространения волны
v = ω / k . (3)
Тогда ( см. (*) )
Vm/v = Aω / ( ω / k ) = A k .
Vm/v = A k .
Vm/v = 60 ·10 ⁻ ⁶ · 5,3 = 3,2 ·10 ⁻ ⁴ .
в) Относительную деформацию среды найдём дифференцируя (2) по х:
∂ ξ/ ∂ x = ( Acos(ωt – kx) )x ʹ = — Aksin (ωt – kx).
Ответ: a) A/λ = 5,1 ·10 ⁻ ⁵ ;
б) Vm = 0,11 м/с, Vm/v = 3,2 ·10 ⁻ ⁴;
в) ( ∂ ξ/ ∂ x)m = 3,2 ·10 ⁻ ⁴, V m = v · (d ξ/dx)m , где v = 340 м/с – скорость волны .
4.3-3. Что такое амплитуда колебаний скорости частиц среды?
Решение:
Объясню на простом примере. В озере на воде поплавок. Бросьте в воду камешек, от него во все стороны пойдут волны. Поплавок колеблется на волнах. Скорость колебаний поплавка − это скорость колебаний частиц среды (воды). Максимальная скорость колебаний поплавка − это амплитуда колебаний скорости частиц среды.
Амплитуда колебаний скорости частиц среды
Vm = Aω ( A — амплитуда, ω — циклическая частота).
Скорость распространения волны
v = ω / k ( k — волновое число).
A , ω , k определяют из общего вида уравнения бегущей плоской синусоидальной волны
ξ = Acos ( ωt – kx ).
4.3-4. Точечный изотропный источник испускает звуковые колебания с частотой ν = 1,45 кГц. На расстоянии r₁ = 5 м от источника амплитуда смещения частиц среды А₁ = 50 мкм, а в точке А, находящейся на расстоянии r₂ = 10 м от источника, амплитуда смещения в η = 3 раза меньше А₁. Найти:
а) коэффициент затухания волны γ;
б) амплитуду колебаний скорости частиц среды в точке А.
Решение:
ν = 1450 Гц
r₁ = 5 м
А₁ = 50·10⁻⁶ м
r₂ = 10 м
А₂ = А₁/η (η = 3) (*)
а) γ − ?
б) Vm − ? (в точке А)
От данного точечного источника распространяются сферические волны. Для однородной поглощающей среды уравнение сферической волны:
(1)
где ξ − смещение частиц среды; ω = 2πν − циклическая частота; k − волновое число.
а). Из (1) выпишем амплитуду A смещения частиц среды (множитель перед косинусом):
A = (A₀/r)·e⁻ᵞʳ.
Отсюда для r = r₁ и r = r₂ получаем амплитуды смещения частиц среды A₁ и A₂ соответственно
A ₁ = ( A ₀ / r ₁ ) · e ⁻ ᵞ r₁ , (**)
A ₂ = ( A ₀ / r ₂ ) · e ⁻ ᵞ r ₂ . (***)
Делим (**) на (***) и, с учётом (*), получаем:
η = ( r ₂ / r ₁ ) · e ᵞ ⁽ r ₂ ⁻ r₁ ⁾ отсюда η r ₁ / r ₂ = e ᵞ ⁽ r ₂ ⁻ r₁ ⁾ , отсюда, по определению логарифма, имеем
ln ( η r ₁ / r ₂ ) = γ( r ₂ — r ₁ ), отсюда
γ = ln(3 · 5 /10 )/(10 — 5 ) ≈ 0,08 м ⁻ ¹ .
б). Для нахождения скорости смещения частиц среды V найдём частную производную по времени t от (1):
V = ∂ ξ / ∂ t = ( A ₀ / r ) · e ⁻ ᵞ ʳ ·( — ω sin ( ω t — kr ) ).
С учётом ω = 2πν, имеем
V = — ( 2 π ν A ₀ /r ) ·e ⁻ ᵞ ʳ ·sin ( ω t-kr ) .
Отсюда амплитуда колебаний скорости частиц среды Vm (множитель перед синусом):
4.3-5. Плоская звуковая волна, частота которой 100 Гц и амплитуда 5 мкм, распространяется со скоростью 300 мс в воздухе, плотность которого равна 1 , 2 кгм ³ . Определить интенсивность волны.
Решение:
ν = 100 Гц
а = 5·10⁻⁶ м
V = 300 мс
ρ = 1,2 кгм³
I − ?
Интенсивность I звуковой волны
I = ρ а² ω ² V /2 и т.к. ω = 2 πν , то
I = ρ а²(2 πν )² V /2.
I = 1,2·(5·10⁻⁶)²·(2·3,14·100)²·300/2 = 1,77·10⁻³ Вт/м².
Ответ: I = 1,77·10⁻³ Вт/м².
4.3-6. Стальная струна длины l = 100 см и диаметра d = 0,50 мм даёт основной тон частоты ν = 256 Гц. Найти силу её натяжения.
Решение:
l = 1 м
d = 0,5·10⁻³ м
ν = 256 Гц
ρ = 7800 кг/м³ (плотность стали)
F − ?
В закреплённой с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны. Основной тон частоты ν колебаний струны:
ν = V/2l, отсюда
V = 2lν, (1)
где
− фазовая скорость поперечных волн в струне. Отсюда
F = V²ρ₁ , (2)
где ρ₁ = m/l − линейная плотность струны, m = ρV₀ − масса струны, V₀ = (πd²/4)l = πd²l/4 − объём струны.
Имеем: ρ₁ = ρV₀/l = ρ(πd²l/4)/l = ρπd²/4. Получили
ρ₁ = ρπd²/4. (3)
Подставляя в (2) V из (1) и ρ₁ из (3), получим силу натяжения F струны
F = (2lν)²ρπd²/4, или
F = πρ(lνd)².
F = 3,14·7800· (1·256·0,5·10⁻³)² ≈ 401,3 Н.
Ответ: F = πρ(lνd)² ≈ 401,3 Н.
_______________________________________________________________________________________________
4.4. Электромагнитные волны. Излучение.
4.4-1. Электромагнитная волна с частотой 6 · 10 ¹⁴ Гц распространяется в стекле, показатель преломления которого 1,5. Какова скорость волны в стекле и значение волнового числа?
Решение:
ν = 6 · 10¹⁴ Гц
n = 1,5
c = 3 · 10⁸ м/с (скорость света в вакууме)
V – ? k – ?
Скорость V волны в стекле:
V = c / n . (1)
Длина волны в стекле:
λ = V / ν = c /( nν ). (*)
Волновое число k:
k = 2 π / λ или с учётом (*)
k = 2 πnν /с. (2)
Вычисления по (1), (2)
V = 3 · 10⁸/1,5 = 2 · 10⁸ м/с.
k = 2 · 3,14 · 1,5 · 6 · 10¹⁴/(3 · 10⁸) = 1,88 · 10⁷ (1/м).
Ответ: V = 2 · 10⁸ м/с; k = 1,88 · 10⁷ (1/м).
4.4-2. Определить показатель преломления призмы из парафина , если его диэлектрическая проницаемость Ԑ = 2 и магнитная проницаемость μ = 1.
Решение:
Ԑ = 2
μ = 1
n – ?
Показатель преломления среды
n = C / V . (1)
С – скорость света в вакууме.
Скорость света в среде
V = C /√( Ԑμ ). (2)
Из (1) и (2) имеем
n = √( Ԑμ ).
n = √(2·1) = 1,41.
Ответ: n = 1,41.
___________________________________________________________________________________
🔥 Видео
МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Урок 370. Механические волны. Математическое описание бегущей волныСкачать

Волновое движение. Механические волны. 9 класс.Скачать

Выполнялка 53.Гармонические колебания.Скачать

Билеты №1 и №2 "Монохроматические волны"Скачать

Консультация к устному экзамену. Механика. Часть 9: "Волны"Скачать

74. Упругие волныСкачать

Урок 325. Колебательное движение и его характеристикиСкачать

Урок 92 (осн). Колебательное движение. МаятникиСкачать

Сбор подписей за выдвижение Надеждина. Орешкин*, Кынев. Утро с Роменским* и Баблоян / 23.01.24Скачать

ВОЛНЫ и ЗВУК физика 9 класс ПерышкинСкачать

Билет №34 "Электромагнитные волны"Скачать

Гармонические колебанияСкачать

Колебания и волны. Часть 2Скачать

Урок 335. Анализ графика гармонических колебанийСкачать

Парадокс электромагнитной волныСкачать


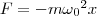































.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
%20%D0%A4%D0%98%D0%97.jpg)
%20%D0%A4%D0%98%D0%97.jpg)
%20%D0%A4%D0%98%D0%97.jpg)



.jpg)