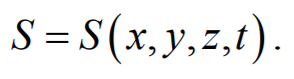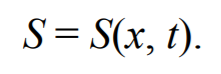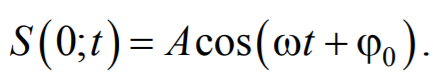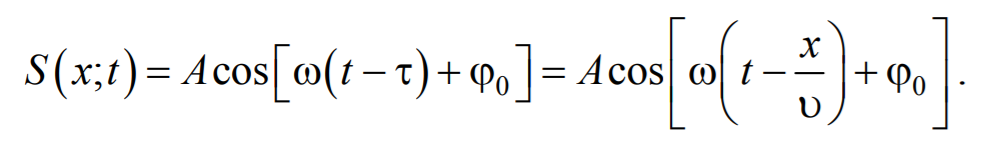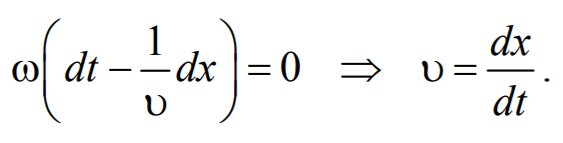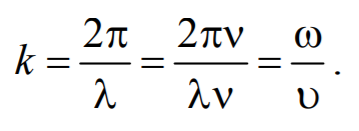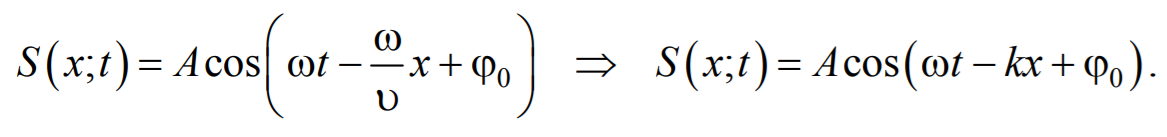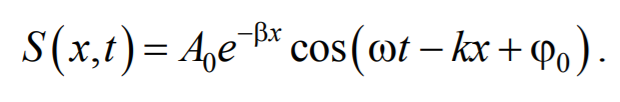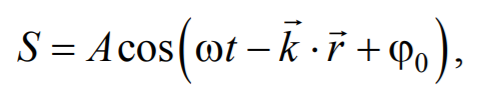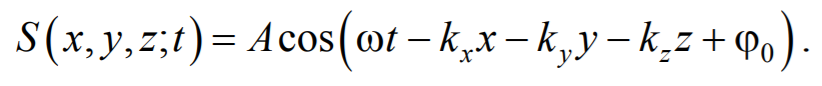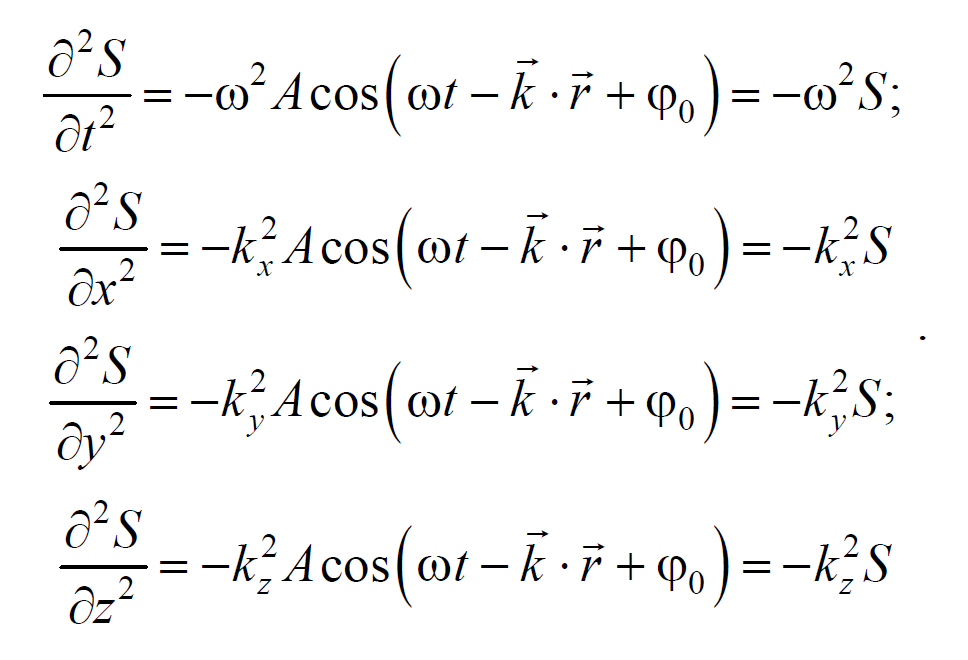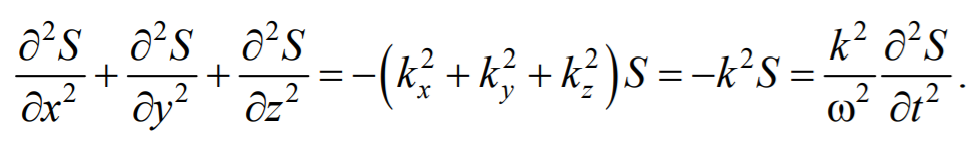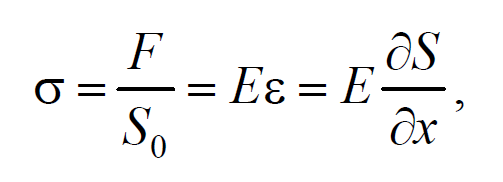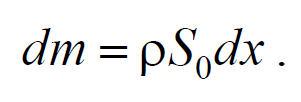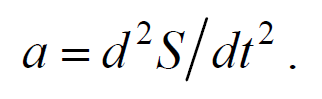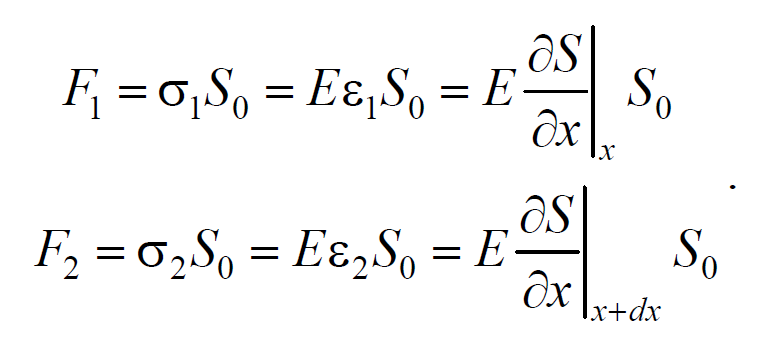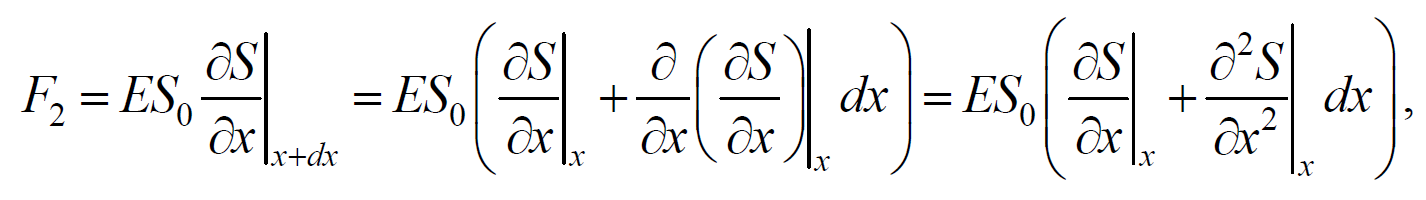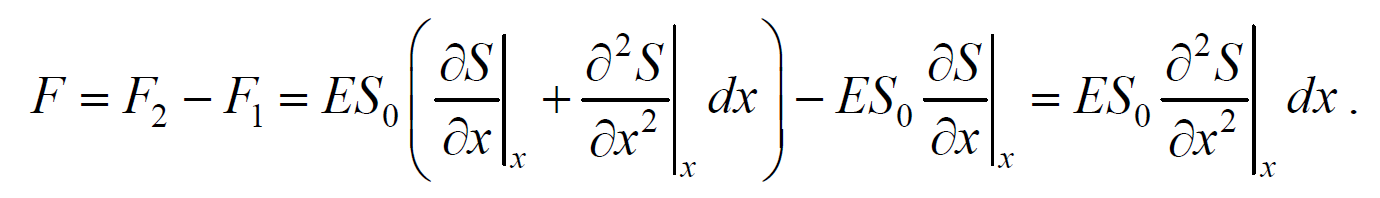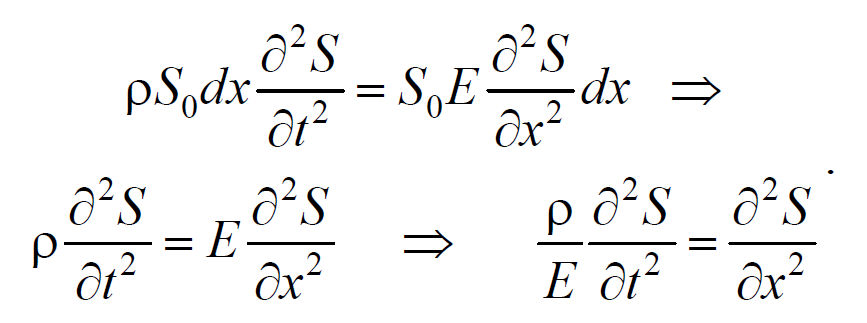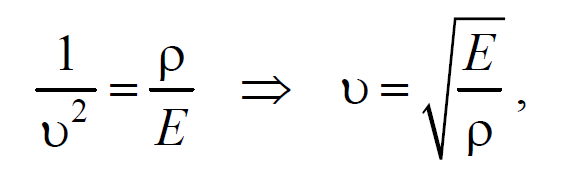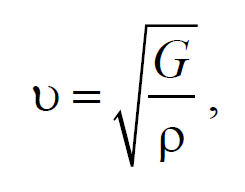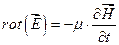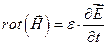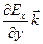Уравнение плоской одномерной гармонической волны (8 видео)

БИЛЕТ 18.Волновое движение. Плоская гармоническая волна. Длина волны, волновое число. Фазовая скорость. Уравнение волны. Одномерное волновое уравнение.

Волновое движение – процесс распространения колебаний в сплошной среде. При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества Среди разнообразных волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Если рассмотреть волновой процесс подробнее, то становится ясным, что колеблются не только частицы, расположенные вдоль оси х, но и совокупность частиц, расположенных в некотором объеме, т. е. волна, распространяясь от источника колебаний, охватывает все новые и новые области пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом. Бегущая волна – волна, которая переносит в пространстве энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова. Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. — уравнение бегущей волны. — если плоская волна распространяется в противоположном направлении. В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид: , где А — const — амплитуда волны; ɷ —циклическая частота; φ₀ — начальная фаза волны; определяемая в общем случае выбором начал отсчета х и t; скорость v распространения волны в уравнении есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью. Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением —дифференциальным уравнением в частных производных — или

Длина́ волны́ — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой . По аналогии с волнами, возникающими в воде от брошенного камня, длиной волны является расстояние между двумя соседними гребнями волны. Одна из основных характеристик колебаний.

Волново́е число́ (также называемое пространственной частотой) — это отношение 2π радиан к длине волны:

Одномерное волновое уравнение – уравнение, описывающее продольные колебания стержня, сечения которого совершают плоскопараллельные колебательные движения, а также поперечные колебания тонкого стержня (струны) и другие задачи.

БИЛЕТ 20 Интерференционное поле от двух точечных источников. Опыт Юнга. Интерферометр Майкельсона. Интерференция в тонких пленках. Стоячие волны.

Для получения когерентных источников света французский физик Огюстен Френель (1788—1827) нашел в 1815 г. простой и остроумный способ. Надо свет от одного источника разделить на два пучка и, заставив их пройти различные пути, свести вместе. Тогда цуг волн, испущенных отдельным атомом, разделится на двакогерентных цуга. Так будет для цугов волн, испускаемых каждым атомом источника. Свет, испускаемый одним атомом, дает определенную интерференционную картину. При наложении этих картин друг на друга получается достаточно интенсивное распределение освещенностина экране: интерференционную картину можно наблюдать. Имеется много способов получения когерентных источников света, но суть их одинакова. С помощью разделения пучка на две части получают два мнимых источника света, дающих когерентные волны. Для этого используют два зеркала (бизеркала Френеля), бипризму (две призмы, сложенные основаниями), билинзу (разрезанную пополам линзу с раздвинутыми половинами) и др. Условие максимума: Если в оптической разности хода волн укладывается четное число полуволн или целое число волн, то в данной точке экрана наблюдается усиление интенсивности света (max): Условие минимума: Если в оптической разности хода волн укладывается нечетное число полуволн, то в точке минимум:

В этом опыте Юнг поток света направил на непрозрачную пластинку с двумя очень маленькими отверстиями, за которой находился экран. Если придерживаться господствовавшей в то время корпускулярной теории света, то на экране он должен был увидеть две светящиеся точки. Вместо этого на экране он увидел чередующиеся светлые и тёмные полосы. Причём самая яркая из них находилась на экране посередине между отверстиями на перегородке, чего быть вообще-то не должно. Юнг объяснил возникновение полос явлением интерференции света. На экране светлые полосы соответствуют точкам, в которых фазы волн одинаковы, а тёмные — точкам, в которых фазы волн противоположны.

Интерферометр Майкельсона — двухлучевой интерферометр, изобретённый Альбертом Майкельсоном. Данный прибор позволил впервые [1] измеритьдлину волны света. В опыте Майкельсона интерферометр был использован Майкельсоном для проверки гипотезы о светоносном эфире. [1]

Конструктивно состоит из светоделительного зеркала, разделяющего входящий луч на два, которые в свою очередь, отражаются зеркалом обратно. На полупрозрачном зеркале разделённые лучи вновь направляются в одну сторону, чтобы, смешавшись на экране, образовать интерференционную картину. Анализируя её и изменяя длину одного плеча на известную величину, можно по изменению вида интерференционных полос измерить длину волны, либо, наоборот, если длина волны известна, можно определить неизвестное изменение длин плеч. Радиус когерентности изучаемого источника света или другого излучения определяет максимальную разность между плечами интерферометра.

Интерференционные полосы равного наклона. При освещении тонкой пленки происходит наложение волн от одного и того же источника, отразившихся от передней и задней поверхностей пленки. При этом может возникнуть интерференция света. Если свет белый, то интерференционные полосы окрашены. Интерференцию в пленках можно наблюдать на стенках мыльных пузырей, на тонких пленках масла или нефти, плавающих на поверхности воды, на пленках, возникающих на поверхности металлов или зеркала

Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называетсястоячей волной. Практически стоячие волны возникают при отражении от преград.

Содержание

Лекция №9. Механические волны
6.1. Распространение колебаний в упругой среде
6.2. Уравнение плоской волны
6.3. Волновое уравнение
6.4. Скорость распространения волн в различных средах
Гармоническая волна
🔍 Видео

Видео:10й класс; Физика; "Уравнение плоской волны"Скачать

Лекция №9. Механические волны

6.1. Распространение колебаний в упругой среде

Механические колебания, распространяющиеся в упругой среде (твердой, жидкой или газообразной), называются механическими или упругими волнами .

Процесс распространения колебаний в сплошной среде называется волновым процессом или волной. Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение. Они лишь совершают колебания около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества .

В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны.

Упругая волна называется продольной , если колебания частиц среды происходят в направлении распространения волны. Продольные волны связаны с объемной деформацией растяжения − сжатия среды, поэтому они могут распространяться как в твердых телах, так и в жидкостях и газообразных средах.

Упругая волна называется поперечной , если колебания частиц среды происходят в плоскостях, перпендикулярных к направлению распространения волны Поперечные волны могут возникать только в такой среде, которая обладает упругостью формы, т. е. способна сопротивляться деформации сдвига. Этим свойством обладают только твердые тела.

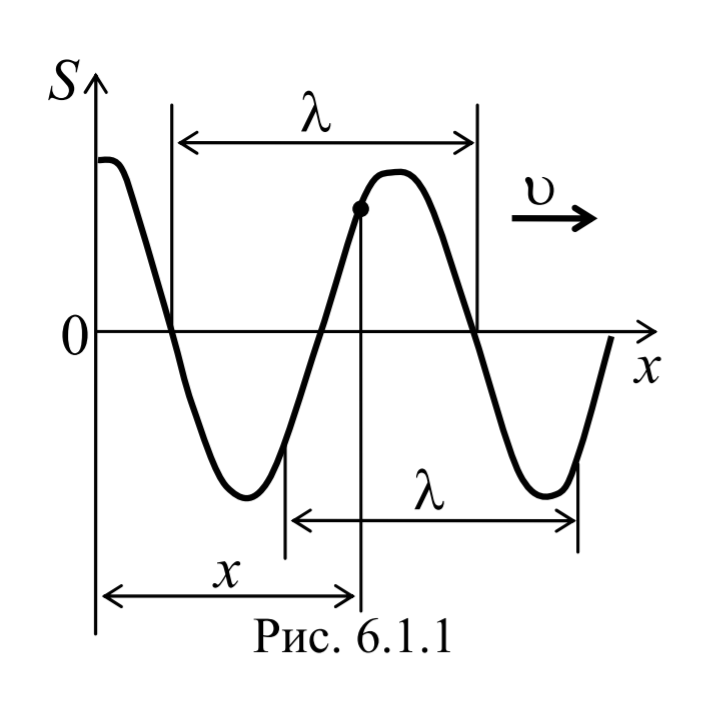
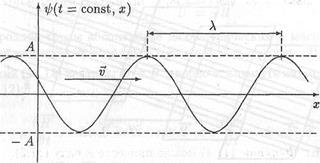
На рис. 6.1.1 представлена гармоническая поперечная волна, распространяющаяся вдоль оси 0х . График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны . Длина волны также равна тому расстоянию, на которое распространяется определенная фаза колебания за период колебаний

Колеблются не только частицы, расположенные вдоль оси 0х , а совокупность частиц, заключенных в некотором объеме. Геометрическое место точек, до которых доходят колебания к моменту времени t , называется фронтом волны . Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью . Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, а в сферической − множество концентрических сфер.

6.2. Уравнение плоской волны

Уравнением плоской волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x , y , z и времени t

Эта функция должна быть периодической как относительно времени t , так и относительно координат x , y , z . Периодичность по времени вытекает из того, что смещение S описывает колебания частицы с координатами x , y , z , а периодичность по координатам следует из того, что точки, отстоящие друг от друга на расстоянии, равном длине волны, колеблются одинаковым образом.

Предположим, что колебания носят гармонический характер, а ось 0х совпадает с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны оси 0х и, поскольку все точки волновой поверхности колеблются одинаково, смещение S будет зависеть только от координаты х и времени t

Рассмотрим некоторую частицу среды, находящуюся от источника колебаний О на расстоянии х . Пусть колебания точек, лежащих в плоскости х = 0 имеют вид

Найдем вид колебания точек в плоскости, соответствующей произвольному значению х . Для того, чтобы пройти путь от плоскости х = 0 до плоскости х , волне требуется время τ = x/υ . Следовательно, колебания частиц, лежащих в плоскости х , будут отставать по времени на τ от колебаний частиц в плоскости х = 0 и описываться уравнением

где А − амплитуда волны; ϕ₀ − начальная фаза волны (определяется выбором начал отсчета х и t ).

Зафиксируем какое-либо значение фазы ω(t-x/υ)+ϕ₀=const. Это выражение определяет связь между временем t и тем местом х , в котором фаза имеет фиксированное значение. Продифференцировав данное выражение, получим

Таким образом, скорость распространения волны есть скорость перемещения фазы, и называется фазовой скоростью .

При υ > 0 волна распространяется в сторону возрастания х . Волна, распространяющаяся в противоположном направлении, описывается уравнением

Придадим уравнению плоской волны симметричный относительно х и t вид. Для этого введем величину $$k = $$ , которая называется волновым числом , которое можно представить в виде

Тогда уравнение плоской волны будет иметь вид

Мы предполагали, что амплитуда колебаний не зависит от х . Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. При распространении в поглощающей энергию среде интенсивность волны с удалением от источника колебаний постепенно уменьшается, т. е. наблюдается затухание волны. В однородной среде такое затухание происходит по экспоненциальному закону A=A₀e −βx . Тогда уравнение плоской волны для поглощающей среды имеет вид

6.3. Волновое уравнение

Уравнение плоской волны, распространяющейся в произвольном направлении, будет иметь вид

где r − радиус-вектор, точки волны; r =k× n − волновой вектор ; n − единичный вектор нормали к волновой поверхности

Волновой вектор − это вектор, равный по модулю волновому числу k и имеющий направление нормали к волновой поверхности называется.

Перейдем от радиус-вектора точки к ее координатам x , y , z 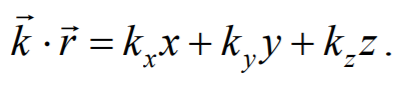Тогда уравнение (6.3.2) примет вид

Установим вид волнового уравнения. Для этого найдем вторые частные производные по координатам и времени выражение (6.3.3)

Сложив производные по координатам, и с учетом производной по времени, получим

6.4. Скорость распространения волн в различных средах

Для определения скорости упругих волн в упругой среде рассмотрим продольную плоскую волну, распространяющуюся в направлении оси 0х . Выделим в среде цилиндрический объем с площадью основания S₀ и высотой d_x . Смещения S частиц с разными х в каждый момент времени оказываются различными. Если основание цилиндра с координатой х имеет в некоторый момент времени смещение S , то смещение основания с координатой x+dx будет S+dS . Тогда, рассматриваемый объем деформируется и получает удлинение dS или относительную деформацию ε=∂S/∂x (деформации растяжения). Наличие деформации свидетельствует о существовании нормального напряжения σ , которое при малых деформациях пропорционального величине деформации. По закону Гука для деформации растяжения − сжатия

где Е − модуль Юнга среды.

Из зависимости смещения от координаты x видно, что относительная деформация ∂S/∂x , а также, и напряжение σ в фиксированный момент времени зависят от х . В соответствии с этим, продольная волна состоит из чередующихся разрежений и сжатий среды.

Теперь для цилиндрического объема запишем уравнение движения. Масса этого объема

где ρ − плотность недеформированной среды.

Ввиду малости dx можно считать ускорение всех точек цилиндра одинаковым и равным

Тогда этот участок объема будет растянут под влиянием сил F₁ и F₂ , приложенных к основаниям цилиндра в данный момент времени. Силы, действующие на левое и правое основание цилиндра равны, соответственно

После разложения силы F₂ в ряд, получим

и результирующая F₁ , F₂ сил, действующая на элемент объема равна

Используя основное уравнение динамики поступательного движения (2.1.2) и, подставив значения массы, ускорения и силы, получим

Из сравнения этого уравнения с волновым уравнением для плоской волны (6.3.6) $$=$$ , получим

где Е − модуль Юнга.

Полученное уравнение определяет фазовую скорость продольных упругих волн.

Если проделать аналогичные преобразования для поперечных упругих волн, то фазовая скорость поперечных упругих волн будет иметь следующий вид

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармоническая волна

Волна называется гармонической, если она описывается функцией,

ψ(t,х) = А cos(ωt-kx + a), (11.4)

где А — амплитуда волны; ω — частота; к — волновое число; а — начальная фаза;

— фаза волны. Функцию (11.4) можно привести к виду (11.2):

видно, что скорость гармонической волны связана с частотой и волновым числом соотношением

Для того чтобы получить зависимость величины ψ от времени t, которая описывает ее изменения со временем в данной точке пространства, следует положить в формуле (11.4) х = const. Так как функция (11.4) при х = const описывает гармонические колебания, говорят, что гармоническая волна создает в произвольной точке пространства гармонические колебания.

T=2π/ω — период волны, а (11.7)

— длиной волны. Если фаза (11.5) волны получит приращение 2π, то, значение функции (11.4) останется прежним. Поэтому при х= const функция (11.4) принимает одно и то же значение для всех моментов времени, которые отличаются одно от другого на пТ, где п — целое число; а при t = const значения функции (11.4) в различных точках пространства совпадают, если координаты этих точек отличаются друг от друга на пλ. График зависимости величины ψ(t,х) от координаты х при t = const для случая, когда вдоль оси х распространяется гармоническая волна, показан на рис. 11.2.

Рис. 11.2. Гармоническая волна

11.3. Волны впространстве

Пусть физическая величина ψ распределена в пространстве, и это распределение меняется со временем. Говорят, что функция ψ = ψ(t,r) описывает волну, распространяющуюся в пространстве, если она удовлетворяет уравнению

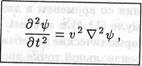Уравнение плоской одномерной гармонической волны

Волна называется плоской, если существует такая система декартовых координат, в которой функция ψ зависит только от одной из координат. Если этой координатой является х, то уравнение (11.9) сводится к (11.1). В произвольной прямоугольной системе декартовых координат плоская гармоническая волна описывается функцией

ψ(t,r) = A cos(ωt-kr + a), (11.10

где вектор кназывается волновым. В том, что эта функция является решением уравнения (11.9), нетрудно убедиться непосредственной подстановкой.

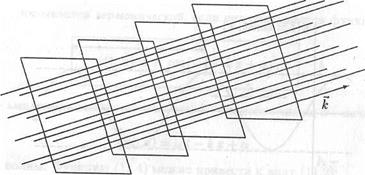
Рис. 11.3. Фазовые поверхности и лучи, вдоль которых распространяется в пространстве плоская волна

φ(t, r) = ωt –kr+a

называется фазой плоской волны. Поверхность

φ(t = const, r) = const, или kr= const

постоянной фазы (11.11) является плоскостью, к которой вектор кперпендикулярен. Такие поверхности называют фазовыми, или волновыми, а линии, перпендикулярные к фазовым поверхностям, называют лучами. Для плоской волны лучами являются прямые, параллельные волновому вектору. Этот вектор указывает направление распространения волны, а его модуль (волновое число), частота и скорость волны связаны соотношением (11.6). На рис. 11.3 изображены фазовые поверхности и лучи плоской волны.

11.4. Плоские электромагнитные волны *

Рассмотрим электромагнитное поле в пространстве, заполненном однородным диэлектриком, в котором отсутствуют свободные заряды и электрические токи, т.е. объемная плотность связанных зарядов и плотность тока равны нулю:

ρ=0, j=0

В таком случае уравнения Максвелла (10.1) — (10.4) принимают вид

(11.12)

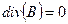
D =εE, В =μH. (10.13)

Для однородной среды абсолютные диэлектрическая и магнитная проницаемости вещества постоянны: ε = const и μ = const. При помощи

соотношений (11.13) векторы D и В удобно исключить из системы уравнений (11.12):

→ divE=0

→

→divH=0

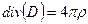
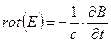
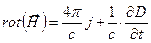
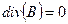
Пусть векторы Е и Н зависят только от t и у:

Покажем, что эти функции могут быть решениями уравнений (11.14), а также, что среди решений уравнений (11.14) такого вида есть функции, описывающие плоские электромагнитные волны, распространяющиеся вдоль оси у.

Вычислим ротор и дивергенцию вектора E(t, у)

rot E = = +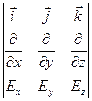

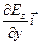
div =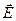

С учетом этих формул подстановка векторов (11.15) в равенства (11.14) приводит к системе уравнений

= (11.16)

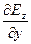
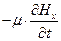
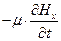
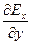
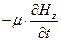
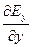
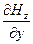
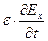
0= (11.17)

— = (11.18)

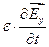
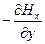
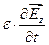
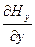
=0 (11.19)

= (11.20)

0= (11.21)

= (11.22)

=0 (11.23)

Из уравнений (11.19) и (11.21) следует, что Е_y = const. Очевидно, что постоянное электрическое поле в электромагнитной волне отсутствует. Поэтому положим

Аналогично, уравнения (11.17) и (11.23) приводят к равенству

Оставшиеся неиспользованными уравнения можно разделить на две независимые системы. Первая состоит из уравнений (11.16) и (11.22) для функций E_z и Н_х, а вторая — из уравнений (11.18) и (11.20) для функций Е_х и Н_г. Выпишем уравнения первой системы:

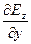
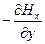
Исключим Н_х из этой системы. Для этого продифференцируем уравнение (11.16) по у, а уравнение (11.22) — по i. После несложных преобразований придем к уравнению

= ; (16.26)

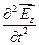
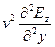
v= 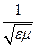(11.27)

Уравнение (11.26) есть волновое уравнение. Одно из его решений, описывающих гармоническую волну, имеет вид

где E_m — амплитуда волны. Эта волна распространяется вдоль оси у в сторону возрастания у.

также является решением волнового уравнения (11.26). Эта функция есть плоская гармоническая волна, распространяющаяся вдоль оси у в сторону убывания у.

Найдем функцию H_x(t,y), соответствующую функции (11.28). Для этого подставим выражение (11.28) в уравнения (11.16) и (11.22). Получим:

= -( кЕ_m/μ)sin(ωt- к у + а),

= ωεE_m sin(ωt- ky +a)

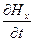
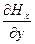
Отсюда с учетом соотношений (11.6) и (11.27) найдем, что

Н_т = 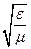Е_т (11.30)

В частном случае система уравнений (11.18) и (11.20) имеют нулевое

Нетрудно проверить, что функции

при условии (11.30) также являются решениями системы уравнений (11.18) и (11.20).

Итак, найдены решения уравнений Максвелла в виде плоских гармонических волн, распространяющихся вдоль оси у. Решениями уравнений Максвелла могут быть не только плоские гармонические волны. Вдоль оси у могут распространяться электромагнитные волны более сложной формы. Например, это может быть произвольная суперпозиция плоских гармонических волн. Для всех этих волн справедливы равенства (11.24) и (11.25). Вообще все электромагнитные волны обладают таким свойством. Проекции векторов Е и H на направление, вдоль которого распространяется электромагнитная волна всегда равны нулю. Это свойство называют поперечностъю электромагнитных волн.

Дата добавления: 2015-06-12 ; просмотров: 3857 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ