- 6.1. Распространение колебаний в упругой среде
- 6.2. Уравнение плоской волны
- 6.3. Волновое уравнение
- 6.4. Скорость распространения волн в различных средах
- Уравнение плоской волны, распространяющейся в упругой среде, имеет вид s = 10-8 sin(6280t – 1,256x). Определить длину волны, скорость её распространения и частоту колебаний.
- Описание и исходные данные задания, 50% решения + фотография:
- Механические волны в упругой среде
- 📽️ Видео
6.1. Распространение колебаний в упругой среде
Механические колебания, распространяющиеся в упругой среде (твердой, жидкой или газообразной), называются механическими или упругими волнами .
Процесс распространения колебаний в сплошной среде называется волновым процессом или волной. Частицы среды, в которой распространяется волна, не вовлекаются волной в поступательное движение. Они лишь совершают колебания около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества .
В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны.
Упругая волна называется продольной , если колебания частиц среды происходят в направлении распространения волны. Продольные волны связаны с объемной деформацией растяжения − сжатия среды, поэтому они могут распространяться как в твердых телах, так и в жидкостях и газообразных средах.
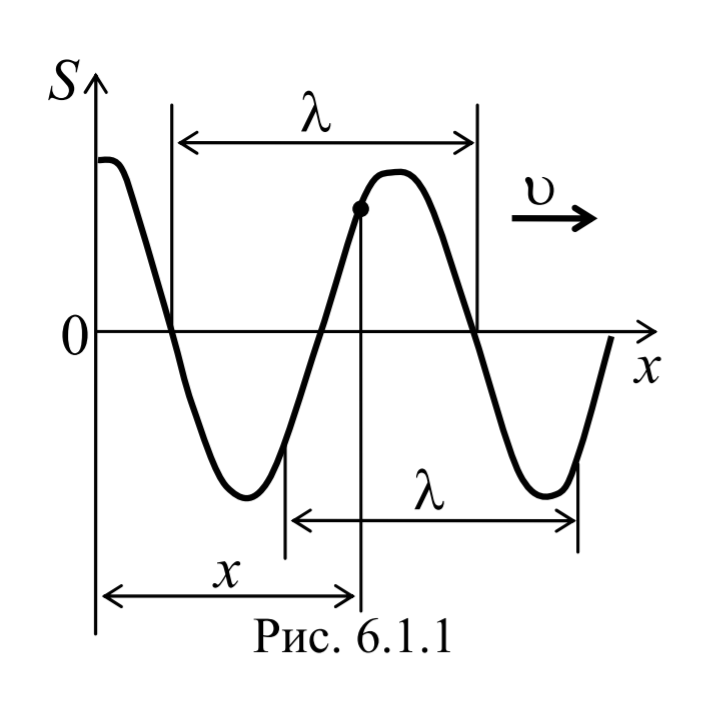
На рис. 6.1.1 представлена гармоническая поперечная волна, распространяющаяся вдоль оси 0х . График волны дает зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны . Длина волны также равна тому расстоянию, на которое распространяется определенная фаза колебания за период колебаний
Колеблются не только частицы, расположенные вдоль оси 0х , а совокупность частиц, заключенных в некотором объеме. Геометрическое место точек, до которых доходят колебания к моменту времени t , называется фронтом волны . Фронт волны представляет собой ту поверхность, которая отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникли. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью . Волновую поверхность можно провести через любую точку пространства, охваченного волновым процессом. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно волна в этих случаях называется плоской или сферической. В плоской волне волновые поверхности представляют собой множество параллельных друг другу плоскостей, а в сферической − множество концентрических сфер.
6.2. Уравнение плоской волны
Уравнением плоской волны называется выражение, которое дает смещение колеблющейся частицы как функцию ее координат x , y , z и времени t
Эта функция должна быть периодической как относительно времени t , так и относительно координат x , y , z . Периодичность по времени вытекает из того, что смещение S описывает колебания частицы с координатами x , y , z , а периодичность по координатам следует из того, что точки, отстоящие друг от друга на расстоянии, равном длине волны, колеблются одинаковым образом.
Предположим, что колебания носят гармонический характер, а ось 0х совпадает с направлением распространения волны. Тогда волновые поверхности будут перпендикулярны оси 0х и, поскольку все точки волновой поверхности колеблются одинаково, смещение S будет зависеть только от координаты х и времени t
Рассмотрим некоторую частицу среды, находящуюся от источника колебаний О на расстоянии х . Пусть колебания точек, лежащих в плоскости х = 0 имеют вид
Найдем вид колебания точек в плоскости, соответствующей произвольному значению х . Для того, чтобы пройти путь от плоскости х = 0 до плоскости х , волне требуется время τ = x/υ . Следовательно, колебания частиц, лежащих в плоскости х , будут отставать по времени на τ от колебаний частиц в плоскости х = 0 и описываться уравнением
где А − амплитуда волны; ϕ0 − начальная фаза волны (определяется выбором начал отсчета х и t ).
Зафиксируем какое-либо значение фазы ω(t-x/υ)+ϕ0=const. Это выражение определяет связь между временем t и тем местом х , в котором фаза имеет фиксированное значение. Продифференцировав данное выражение, получим
Таким образом, скорость распространения волны есть скорость перемещения фазы, и называется фазовой скоростью .
При υ > 0 волна распространяется в сторону возрастания х . Волна, распространяющаяся в противоположном направлении, описывается уравнением
Придадим уравнению плоской волны симметричный относительно х и t вид. Для этого введем величину $$k = $$ , которая называется волновым числом , которое можно представить в виде
Тогда уравнение плоской волны будет иметь вид
Мы предполагали, что амплитуда колебаний не зависит от х . Для плоской волны это наблюдается в том случае, когда энергия волны не поглощается средой. При распространении в поглощающей энергию среде интенсивность волны с удалением от источника колебаний постепенно уменьшается, т. е. наблюдается затухание волны. В однородной среде такое затухание происходит по экспоненциальному закону A=A0e −βx . Тогда уравнение плоской волны для поглощающей среды имеет вид
6.3. Волновое уравнение
Уравнение плоской волны, распространяющейся в произвольном направлении, будет иметь вид
где r − радиус-вектор, точки волны; r =k× n − волновой вектор ; n − единичный вектор нормали к волновой поверхности
Волновой вектор − это вектор, равный по модулю волновому числу k и имеющий направление нормали к волновой поверхности называется.
Перейдем от радиус-вектора точки к ее координатам x , y , z 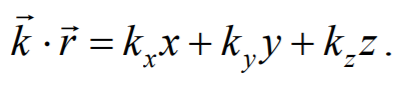
Установим вид волнового уравнения. Для этого найдем вторые частные производные по координатам и времени выражение (6.3.3)
Сложив производные по координатам, и с учетом производной по времени, получим
6.4. Скорость распространения волн в различных средах
Для определения скорости упругих волн в упругой среде рассмотрим продольную плоскую волну, распространяющуюся в направлении оси 0х . Выделим в среде цилиндрический объем с площадью основания S0 и высотой dx . Смещения S частиц с разными х в каждый момент времени оказываются различными. Если основание цилиндра с координатой х имеет в некоторый момент времени смещение S , то смещение основания с координатой x+dx будет S+dS . Тогда, рассматриваемый объем деформируется и получает удлинение dS или относительную деформацию ε=∂S/∂x (деформации растяжения). Наличие деформации свидетельствует о существовании нормального напряжения σ , которое при малых деформациях пропорционального величине деформации. По закону Гука для деформации растяжения − сжатия
где Е − модуль Юнга среды.
Из зависимости смещения от координаты x видно, что относительная деформация ∂S/∂x , а также, и напряжение σ в фиксированный момент времени зависят от х . В соответствии с этим, продольная волна состоит из чередующихся разрежений и сжатий среды.
Теперь для цилиндрического объема запишем уравнение движения. Масса этого объема
где ρ − плотность недеформированной среды.
Ввиду малости dx можно считать ускорение всех точек цилиндра одинаковым и равным
Тогда этот участок объема будет растянут под влиянием сил F1 и F2 , приложенных к основаниям цилиндра в данный момент времени. Силы, действующие на левое и правое основание цилиндра равны, соответственно
После разложения силы F2 в ряд, получим
и результирующая F1 , F2 сил, действующая на элемент объема равна
Используя основное уравнение динамики поступательного движения (2.1.2) и, подставив значения массы, ускорения и силы, получим
Из сравнения этого уравнения с волновым уравнением для плоской волны (6.3.6) $$=$$ , получим
где Е − модуль Юнга.
Полученное уравнение определяет фазовую скорость продольных упругих волн.
Если проделать аналогичные преобразования для поперечных упругих волн, то фазовая скорость поперечных упругих волн будет иметь следующий вид
Видео:Распространение волн в упругих средах. Звуковые волны | Физика 11 класс #18 | ИнфоурокСкачать

Уравнение плоской волны, распространяющейся в упругой среде, имеет вид s = 10-8 sin(6280t – 1,256x). Определить длину волны, скорость её распространения и частоту колебаний.






Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
№2 306. Уравнение плоской волны, распространяющейся в упругой среде, имеет вид s = 10-8 sin(6280t – 1,256x). Определить длину волны, скорость её распространения и частоту колебаний.
Уравнение плоской волны в общем виде: , где – смещение точек среды с координатой в момент времени ; – амплитуда волны; – циклическая частота; – волновое число. Из заданного уравнения плоской волны следует: рад/с, рад/м. Частота колебаний связана с циклической частотой
| Если вам нужно решить физику, тогда нажмите ➔ заказать контрольную работу по физике. |
| Похожие готовые решения: |
- Уравнение плоской звуковой волны: е = 6•10-6 cos(1900t – 5,72x) м. Найти: 0) частоту колебаний; 1) длину волны; 2) скорость её распространения; 3) расстояние между ближайшими точками волны, колеблющимися в противофазе.
- Уравнение плоской волны, распространяющейся в стержне сечением 10 см2, имеет вид: x = 6•10-6 cos(1900t – 5,7z) м. Определить: частоту колебаний; длину волны; скорость распространения волны в стержне. Плотность материала стержня 4•103 кг/м3.
- Конденсатору ёмкостью 1 мкФ сообщили заряд 5 мкКл, после чего его замкнули на катушку с индуктивностью 5 мГн. Найти максимальную силу тока в катушке.
- Уравнение плоской волны, распространяющейся в упругой среде, имеет вид: s = 10-8 sin(628t – 1,256x). Определить длину волны, скорость её распространения и частоту колебаний.
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Упругие механические волны. 1 часть. 11 класс.Скачать

Механические волны в упругой среде
| Назва | Механические волны в упругой среде |
| Дата конвертації | 04.10.2013 |
| Розмір | 211.59 Kb. |
| Тип | Лекция |
mir.zavantag.com > Математика > Лекция
ЛЕКЦИЯ 9 Механические возмущения (деформации), распространяющиеся в упругой среде, называются упругими волнами. Продольные волны могут распространяться как в твердых телах, так и в жидкостях или газах. Пример продольных волн — звуковые волны в жидкостях и газах. Они представляют собой колебания давления, распространяющиеся в этих средах. В отличие от других видов механического движения среды (например, ее течения) распространение упругих волн в среде не связано с переносом вещества. Частицы, отстоящие друг от друга на расстоянии ^ T ( ‑ скорость распространения, T – период колебаний), колеблются в одинаковой фазе. Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длиной волны . где ‑ частота колебаний. Пусть s — упругое смещение границ выделенного объема от положений равновесия. Применение к данному объему закона движения центра масс приводит к дифференциальному уравнению
где t –время, ρ –плотность материала стержня, E – модуль Юнга.
Решение уравнения (9.1) для волны, распространяющейся в направлении оси x, имеет вид:
где A – амплитуда колебаний частиц среды (амплитуда волны); – циклическая частота колебаний источника, которая равна частоте колебаний частиц среды, вызванных волной. Можно показать, что данное уравнение имеет общий характер,. В трехмерном виде волновое уравнение имеет следующий вид:
Решением этого уравнения является смещение s частиц среды от положений равновесия, как функция координат и времени. s = s(x,y,z, t). Определим смысл величины в уравнениях (9.2) и (9.3), имеющей размерность скорости. Зафиксируем какое-либо значение фазы, в уравнении (9.2), положив
Выражение (9.4) описывает распространение волнового фронта. Продифференцировав (9.4), получим
Скорость распространения волны в приведенных выше уравнениях есть скорость перемещения фазы, поэтому эту скорость называют фазовой скоростью. Из уравнения (9.1) следует
Т.е.фазовая скорость продольных волн в твердых телах зависит от модуля Юнга E и плотности среды . Можно показать, что скорость поперечных волн определяется модулем сдвига:
^ Скорость волн в идеальном газе для адиабатического процесса распространения зависит от абсолютной температуры :
где γ – показатель адиабаты (отношение изобарной и изохорной теплоемкостей газа, γ=сp/сV), R – универсальная газовая постоянная, T — абсолютная температура, μ – молярная масса газа. Функция (9.2) описывает плоскую волну, так как волновой фронт представляет собой плоскость. ^ Уравнение плоской волны можно представить в симметричном виде относительно t и х. Для этого вводится понятие волнового числа k:
Используя (9.7), получим выражение для скорости :
Тогда уравнение волны описывается соотношением Если волну рассматривать на расстоянии значительно большем, чем размеры источника, то источник можно считать точечным. В этом случае в изотропной среде волна будет сферической. Такую волну описывает решение дифференциального уравнения (9.3), представленное в сферических координатах. Уравнение сферической волны имеет вид:
Из (9.9) видно, что амплитуда сферической волны изменяется обратно пропорционально расстоянию от волнового фронта до источника. Зависимость амплитуды волны от расстояния обусловлено тем, что по мере удаления фронта волны от источника за равные промежутки времени в колебательное движение вовлекаются все возрастающие объемы среды. ^ 3. Плотность потока энергии волны. Вектор Умова Выделим в среде, в которой распространяется плоская продольная волна, элементарный объем V = Sx, с площадь поперечного сечения S и длиной Δx, в котором скорости движения частиц
где Используя уравнение плоской волны (9.9) s = Acos(t – kx), выражение (9.10) примет вид:
Выделенный объем V будет обладать потенциальной энергией упругой деформации на величину Δs, равной (см. формулу (3-28)):
В формуле (9.12) k – коэффициент жесткости; Для плоской волны
где Поскольку фазовая скорость волны
Выражения (9.11) и (9.15) показывают, что кинетическая и потенциальная энергия частиц волны меняются в одной фазе. Полная энергия волны в объеме V будет равна Из (9.16) следует, что энергия волны распространяется со скоростью упругой волны. Разделив энергию W на объем V, в котором она содержится, получим плотность энергии волны
Поскольку среднее значение квадрата синуса равно 1/2, то среднее (по времени) значение плотности энергии в каждой точке среды будет равно
Выражение (9.18) справедливо для всех видов волн. Вывод: среда, в которой возникает волна, обладает дополнительной энергией, поступающей от источника колебаний. Эта энергия передается в различные точки среды волной, т. е. волна переносит энергию. Количество энергии dW, переносимое волной через некоторую поверхность в единицу времени, называется потоком энергии Ф через поверхность. Размерность потока энергии совпадает с размерностью мощности, т. е. Дж/с. По определению:
Плотностью потока энергии волны называется вектор
Выразим плотность потока энергии через объемную плотность энергии w. Согласно определению, плотность потока энергии волны равна
где энергия dW = wdtdSn равна энергии, переносимой через попереч- ное сечение параллелепипеда, dSn, перпендикулярное к направлению распространения волны. Объем данного параллелепипеда равен dtdSn (см. рис. 9.2). Направление вектора плотности потока энергии
Таким образом, вектор плотности потока энергии волны равен произведению вектора скорости распространения энергии волны на величину ее объемной плотности. Вектор циональны квадрату амплитуды волны и квадрату частоты волны. Формула (9.20) справедлива для плотности потока энергии волн любого типа. Квазисинусоидальная волна представляет собой совокупность синусоидальных волн, частоты которых мало отличаются от некоторой основной частоты . Такую несинусоидальную волну называют группой волн, или волновым пакетом. Дисперсией. называется зависимость свойства среды (например, скорость распространения волны) от частоты Рассмотрим простейший волновой пакет, образованный двумя плоскими продольными синусоидальными волнами, распространяющимися вдоль оси ОХ. Пусть амплитуды этих волн одинаковы, начальные фазы равны нулю, а частоты и волновые числа несколько различны, но близки друг к другу: Для результирующей волны получим:
Амплитуда А этой волны постоянной не является, а зависит от координаты х и времени: Выражение для амплитуды волнового пакета также является уравнением плоской синусоидальной волны, которая является волной амплитуды колебаний. Фаза этой волны равна: Скорость и распространения энергии волнового пакета наз. групповой скоростью, которая равна фазовой скорости волны амплитуды. Дифференцируя выражение для ФА и полагая ФА = const, получим:
В пределе, когда и Δk стремятся к нулю, получим:
С учетом того, что
Подставив в (9.2) выражение частоты через фазовую скорость
Формула (9.3) устанавливает соотношение между групповой и фазовой скоростью волн, и получила название формулы Рэлея. Скорость и называется групповой скоростью пакета волн. В случае отсутствия дисперсии волн (d/d = 0) групповая скорость волн в пакете совпадает с их фазовой скоростью. Так как скорость группы волн характеризует распространение амплитуды волнового пакета, то групповая скорость определяет скорость распространения энергии волны. ^ 9.2 Интерференция и дифракция волн. Стоячие волны. — волны должны быть синусоидальными, — частоты колебаний волн должны быть одинаковы, такие волны называются монохроматическими, — разность фаз интерферирующих волн не зависит от времени, такие волны называются когерентными, — колебания в волнах совершаются вдоль одного и того же направления. При интерференции волн отсутствует простое суммирование их энергий, интерференция волн приводит к перераспределению энергии колебаний между соседними областями среды. Поэтому явление интерференции не противоречит закону сохранения и превращения энергии. Примером интерференции волн является картина, создаваемая двумя колеблющимися тонкими стержнями, погруженными в жидкость и жестко связанными друг с другом так, что их амплитуды, частоты и начальные фазы одинаковы. На поверхности жидкости будет наблюдаться совокупность гребней и впадин, – максимумов и минимумов. Если волна огибает какое-либо препятствие, то за ним также будет наблюдаться интерференционная картина. Например, волны, исходящие из точек А и В (рис. 9-1), будут когерентными, так как эти точки принадлежат волновому фронту одной и той же волны. Направления колебаний в этих точка также совпадают. Поэтому, в точке О будет наблюдаться интерференционная картина. Такое явление называется дифракцией волны. В результате дифракции колебания наблюдаются даже в тех местах, которые «закрыты» препятствием на пути волны. Все синусоидальные волны распространяются в среде независимо друг от друга, так что результирующее смещение любой частицы среды равно векторной сумме ее смещений, обусловленных каждой из волн в отдельности. Этот результат справедлив для волн любой природы и называется принципом суперпозиции волн. На основе наблюдений Гюйгенсом был предложен принцип, который объясняет распространение волны: каждая точка волнового фронта является источником вторичной сферической волны, а огибающая фронтов вторичных волн является фронтом новой волны. Явления интерференции и дифракции проявляются не только при распространении механических волн, но и световых. Рис. 9.1 Поскольку k = 2/, то имеем
Уравнение (9.5) есть уравнение стоячей волны. Из (9.5) видно, что в каждой точке стоячей волны происходят колебания той же частоты , что и у встречных волн. Величина
амплитуда колебаний максимальна и равна 2А. Эти точки называются пучностями стоячей волны. Координаты пучностей:
В точках, в которых выполняется условие
амплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны. Координаты узлов:
Расстояние между соседними узлами или пучностями равна Стоячие волны энергии не переносят. В пучностях стоячей волны кинетическая энергия максимальна, а в узлах максимальна потенциальная энергия. Человек с нормальным слухом способен воспринимать в форме звука только такие упругие волны, частоты которых не ниже 16 Гц и не выше 20000 Гц. Кроме того, оказывается, что чувствительность нашего уха к волнам различной частоты неодинакова – она максимальна для волн с частотами порядка 1,5–3 кГц. Эти закономерности обусловлены особенностями строения наших органов слуха. Звуковые волны в газах и жидкостях – продольные. В твердых же телах существуют волны обоих типов. По своей природе и физическим свойствам все упругие волны ничем качественно не отличаются друг от друга. В этом можно убедиться по их действию на микрофоны, пьезоэлектрические приборы, регистрирующие колебания давления, и другие измерительные устройства. Распространение продольных звуковых волн в упругой среде связано с периодическими колебаниями давления в каждой точке среды. Эти колебания давления, воздействуя на органы слуха, вызывают ощущение звука, а их частота определяет высоту тона. Области среды, в которых звуковое давление в данный момент времени максимально, называются сгущениями звуковой волны, а области среды, в которых оно минимально, – разрежениями. Установлено, что верхний и нижний пределы частот слышимых упругих волн у различных животных неодинаковы. Поэтому звуком в физике называют любые упругие волны, причем, в отличие от слышимых, волны с частотами, меньшими 16 Гц, называют инфразвуковыми, а волны с частотами выше 20 кГц, – ультразвуковыми. Ультразвуковые волны с частотами порядка 10 9 Гц и выше иногда называют гиперзвуковыми. Верхняя граница частот ультразвуковых волн (в кристаллах порядка 10 12 –10 13 Гц) соответствует частотам, при которых длина этих волн становится соизмеримой с межмолекулярными расстояниями. Изучением упругих волн занимается физическая акустика. Для характеристики звука в акустике используются частота звуковой волны (или спектр частот в случае сложной несинусоидальной звуковой волны) и интенсивность звука. Интенсивностью или силой звука называется физическая величина I, равная модулю среднего значения вектора плотности потока энергии звуковой волны (вектора Умова): Интенсивность звука можно выразить через скорость переноса энергии (групповую скорость) звуковой волны. Согласно формуле (9.19): где u – групповая скорость волны; w – среднее значение объемной плотности энергии. Для синусоидальной волны скорость и совпадает с фазовой скоростью . Тогда средняя по времени объемная плотность энергии w выражается формулой (9.18). Поэтому для интенсивности звука получим выражение:
В Международной системе единиц (СИ) интенсивность звука выражается в ваттах на квадратный метр (Вт/м 2 ). Например порог интенсивности звука на пороге слышимости составляет 10 –12 Вт/м 2 , а интенсивность звука от шума двигателя самолета – около 0,5 Вт/м 2 . Распространение в упругой среде продольных звуковых волн связано с объемной деформацией. Поэтому, давление в каждой точке среды непрерывно колеблется. Оно равно сумме равновесного значения давления среды и добавочного давления (или разрежения) рзв , вызванного деформацией среды и называемого звуковым давлением. Можно показать, что для плоских и сферических синусоидальных волн среднее по времени звуковое давление выражается через силу звука I:
называется среднеквадратичным или эффективным звуковым давлением ( – плотность среды, – скорость звука). Значения эффективного звукового давления составляют от 10 –5 Па (порог слышимости) до 10 Па (шум двигателя самолета). Субъективной оценкой силы слухового ощущения является громкость звука. Громкость звука зависит не только от его эффективного давления, но и от чувствительности уха, которая неодинакова для звуков разной интенсивности и частоты. Так, например, если давление меньше некоторой величины р0 , называемой порогом слышимости, то такой звук ухом не воспринимается. Порог слышимости зависит от частоты звука, достигая минимального значения порядка 2 · 10 –5 Па при частотах ν = l500–3000 Гц. Достаточно интенсивные звуки перестают восприниматься ухом как звуки и вызывают болевое ощущение. Значение давления рэф , соответствующее появлению этого ощущения, называется порогом болевого ощущения. Он также зависит от частоты звука, хотя и в меньшей степени, чем порог слышимости. Порог болевого ощущения максимален при частотах = 500–1000 Гц и составляет около 200 Па. Для сравнения различных звуков одной и той же частоты вводится уровень звукового давления: где рэф – эффективное давление исследуемого звука, имеющего частоту ; р0 = 2 · 10 –5 Па – условный порог слышимости. В зависимости от числового значения коэффициента k в формуле (9.11) величина L выражается в следующих двух единицах: при k = 1 – в белах (Б) а при Опыты показывают, что две звуковые волны, уровни звукового давления которых одинаковы, а частоты не совпадают, воспринимаются ухом как звуки неодинаковой громкости. Это явление обусловлено зависимостью чувствительности наших органов слуха от частоты звука. Поэтому уровень звукового давления не может служить исчерпывающей характеристикой его громкости. Для сравнения громкости звуков всевозможных частот вводится понятие об уровне громкости. Уровнем громкости звука называется физическая величина, равная уровню звукового давления равногромкого с ним «эталонного звука», частота которого = 1 кГц. Уровень громкости звука выражается в фонах. Уровень громкости звука равен 1 фону, если уровень звукового давления равногромкого с ним «эталонного звука» ( = 1000 Гц) равен 1 дБ. Найдем связь между и ν0 для простейшего случая равномерного движения точечного источника звука ^ И (рис. 9-2) и наблюдателя Н вдоль соединяющей их прямой линии Рис. 9-2 В случае движения источника звука (рис. 9-2) за время ^ T сам источник перемещается вправо на расстояние 1Т . Поэтому, расстояние между двумя соседними сгущениями, т. е. длина волны , уменьшится на величину 1Т, а частота ν1 , регистрируемая неподвижным наблюдателем, соответственно увеличится: Формула (9.12) объясняет различие высоты тона звукового сигнала приближающегося к наблюдателю и удаляющегося от него источника звука (например, поезда). В первом случае 1 > 0 и ν1 > ν0 , а во втором 1 навстречу источнику звука (рис. 9-2), то число сгущений звуковой волны, регистрируемых наблюдателем за 1 с: где = 2 /λ1 = (2 /)ν1 – дополнительное число сгущений, регистрируемых наблюдателем в результате перемещения за 1 с на расстояние, численно равное его скорости 2. Таким образом, регистрируемая частота и частота источника ν0 связаны соотношением:
Полученная формула справедлива для встречного движения
Если источник и наблюдатель движутся в направлении распространения скорости звуковой волны, то скорости 1 и 2 в формуле 📽️ ВидеоРаспространение колебаний в среде. Волны | Физика 9 класс #28 | ИнфоурокСкачать  Физика 11 класс (Урок№2 - Механические волны.)Скачать  5.6 Механические волны. Виды волнСкачать  Физика. 11 класс. Упругие механические волны. Уравнение бегущей и стоячей волны /16.11.2020/Скачать  10й класс; Физика; "Уравнение плоской волны"Скачать  Физика 9 класс. §28 Распространение колебаний в среде. ВолныСкачать  74. Упругие волныСкачать  Урок 95 (осн). Механические волны. ЗвукСкачать  Получение уравнения плоской бегущей волны.Скачать  Механические модели волн. 1.Скачать  Тема 6. Распространение колебаний в упругой среде. Волны. Частота, длина, скорость распространенияСкачать  Волновое уравнение для волн в упругой среде.Скачать  🌊 Продольные и поперечные волны ⚛ ФизикаСкачать 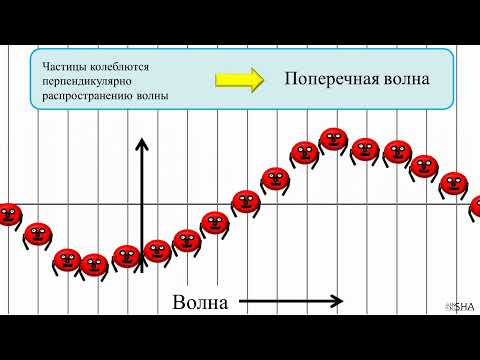 Лекция 2 ВолныСкачать  МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать  Волновое движение. Механические волны. 9 класс.Скачать  Урок 370. Механические волны. Математическое описание бегущей волныСкачать  Упругие механические волны. 2 часть. 11 класс.Скачать  |

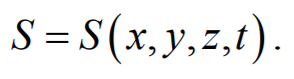
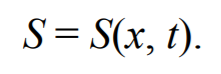
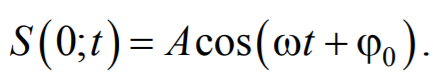
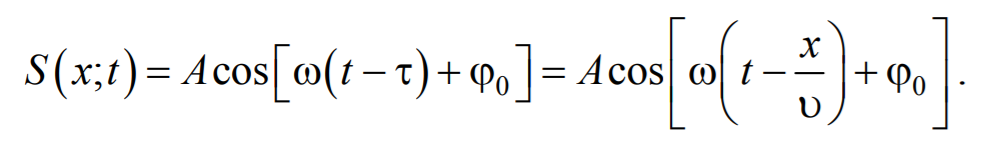
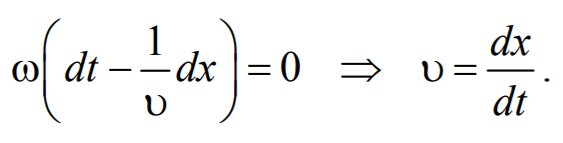

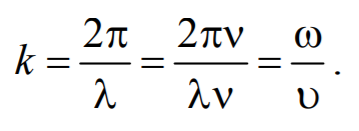
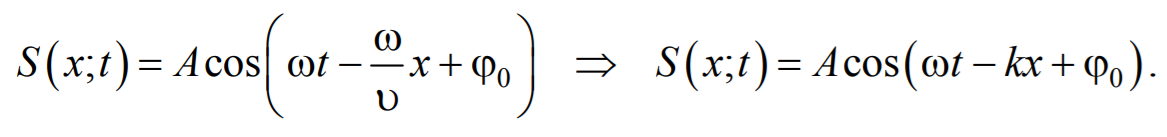
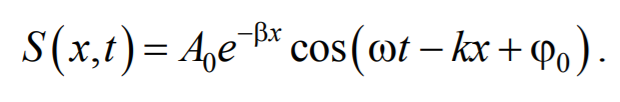
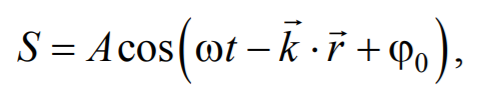
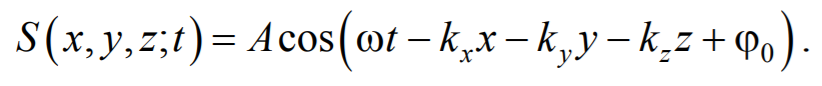
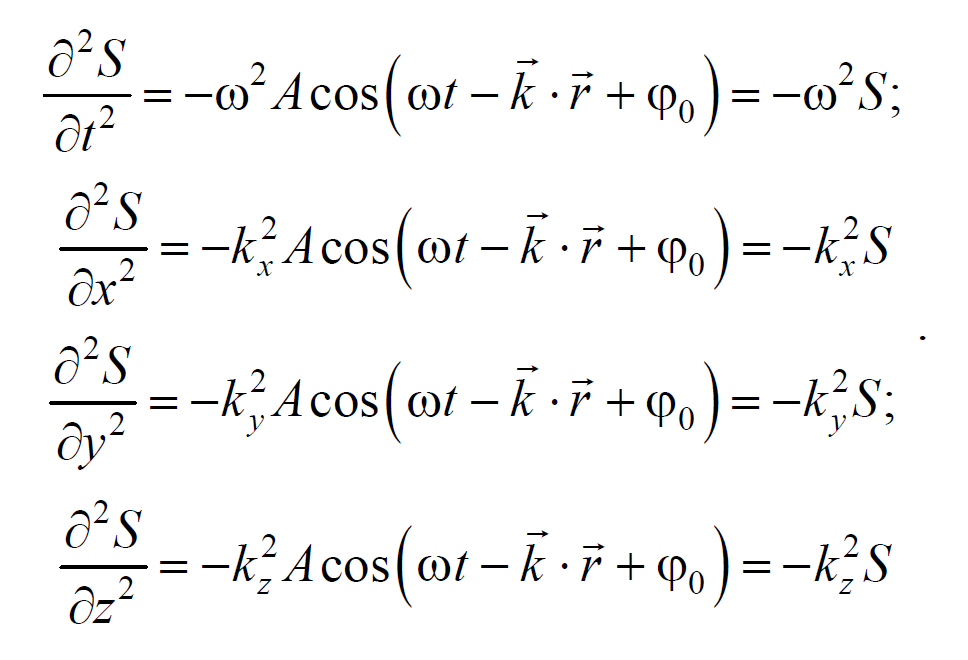
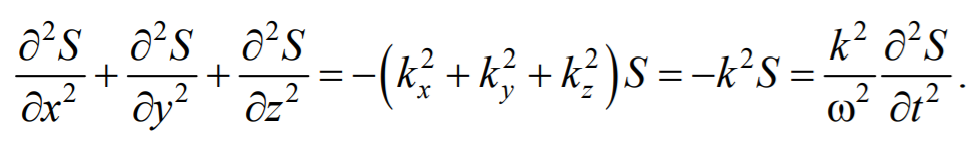
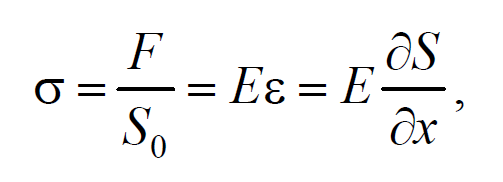
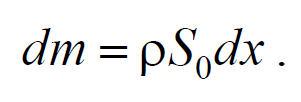
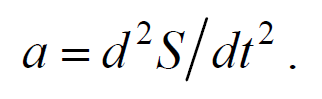
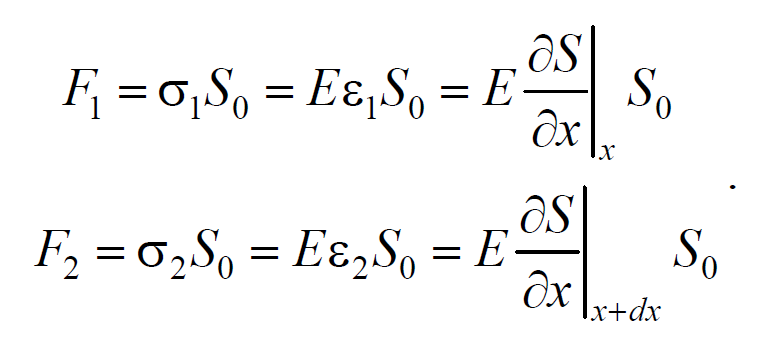
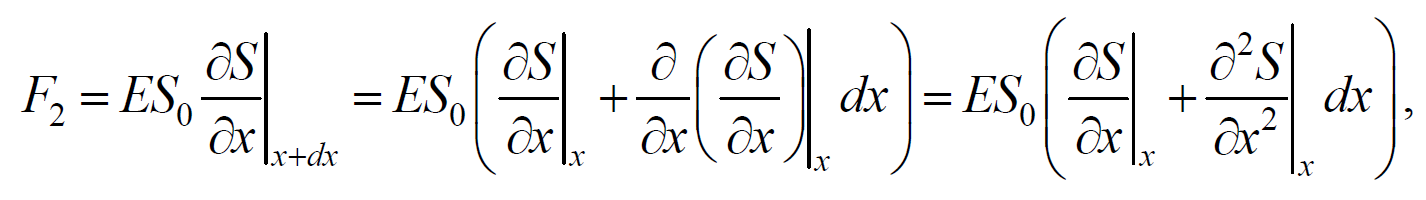
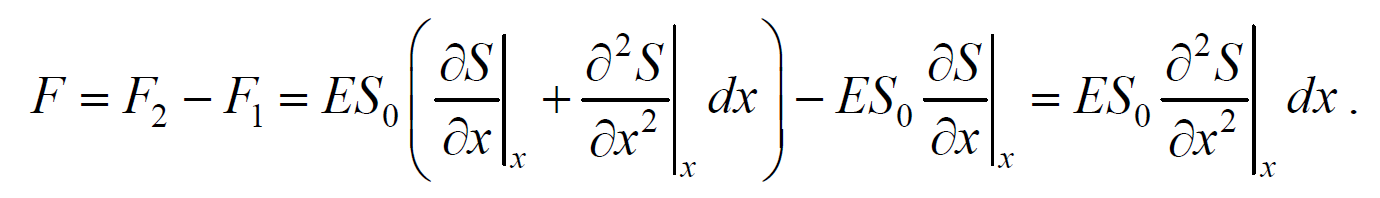
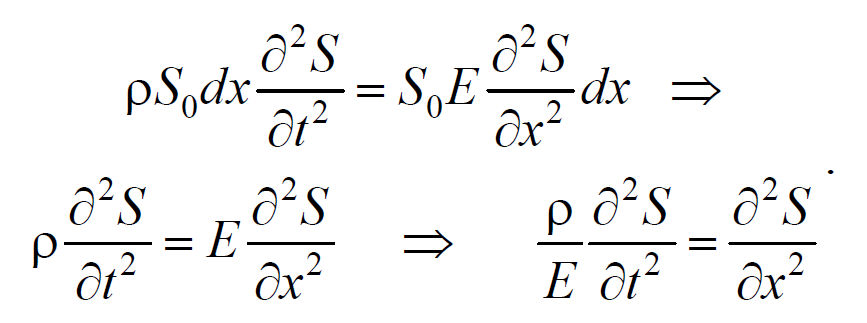
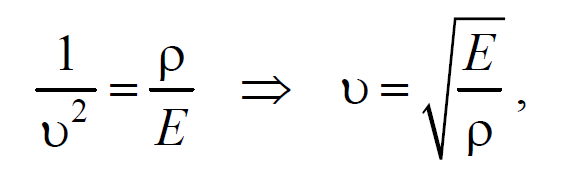
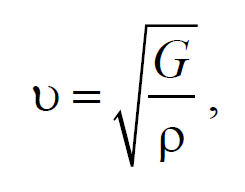


 , (9.1)
, (9.1)
 , (9.2)
, (9.2) , (9.3)
, (9.3) .
. . (9.4)
. (9.4) . (9.5)
. (9.5) .
. .
. ,
, . (9.6)
. (9.6) . (9.7)
. (9.7) . (9.9)
. (9.9) и относительные деформации
и относительные деформации  в каждой точке объема неизменны. Частица массой m и объемом V обладает кинетической энергией, равной
в каждой точке объема неизменны. Частица массой m и объемом V обладает кинетической энергией, равной , (9.10)
, (9.10) ‑ плотность среды.
‑ плотность среды. . (9.11)
. (9.11) . (9.12)
. (9.12) – модуль Юнга;
– модуль Юнга;  ‑ относительная деформация объема среды.
‑ относительная деформация объема среды. , (9.13)
, (9.13) ‑ волновое число. С учетом формулы (9.13):
‑ волновое число. С учетом формулы (9.13): (9.14)
(9.14) , то
, то . (9.15)
. (9.15) . (9.17)
. (9.17) . (9.18)
. (9.18) .
. , направленный в сторону распространения волны и численно равный отношению потока энергии dΦ, сквозь малый элемент dS поверхности к площади dSn проекции этого элемента на плоскость, перпендикулярную к направлению распространения волны:
, направленный в сторону распространения волны и численно равный отношению потока энергии dΦ, сквозь малый элемент dS поверхности к площади dSn проекции этого элемента на плоскость, перпендикулярную к направлению распространения волны: .
. , (9.19)
, (9.19) распространения волны, т. е.
распространения волны, т. е. . (9.20)
. (9.20)
 /
/ .
. . (9.21)
. (9.21) , формула (9.1) примет вид:
, формула (9.1) примет вид: . (9.22)
. (9.22) , и выполнив дифференцирование, получим:
, и выполнив дифференцирование, получим: . (9.23)
. (9.23)
 . (9.5)
. (9.5) является амплитудой стоячей волны. В точках, в которых выполняется условие
является амплитудой стоячей волны. В точках, в которых выполняется условие , (n = 0, 1, 2, …), (9.6)
, (n = 0, 1, 2, …), (9.6) , (n = 0, 1, 2, 3, …). (9.7)
, (n = 0, 1, 2, 3, …). (9.7) , (n = 0, 1, 2, …),
, (n = 0, 1, 2, …), , (n = 0, 1, 2, …). (9.8)
, (n = 0, 1, 2, …). (9.8) и называется длиной стоячей волны.
и называется длиной стоячей волны. . (9.10)
. (9.10) .
.

 (9.12)
(9.12) . (9.13)
. (9.13) . (9.14)
. (9.14)