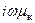Уравнение плоской электромагнитной волны диэлектрическая проницаемость (7 видео)

4.1. Плоская электромагнитная волна в диэлектрике. Скорость распространения электромагнитной волны

При исследовании процессов в переменном электромагнитном поле пользуются полной системой уравнений Максвелла.

Здесь — плотность тока переноса

где r₊ и r_— – объемная плотность положительно заряженных частиц и отрицательно заряженных частиц, перемещающихся в пространстве со скоростью соответственно.

Для плоской, поляризованной электромагнитной волны, излучаемой источниками, не содержащими постоянных токов и зарядов (антенна), и распространяющейся в идеальном диэлектрике (g=0), уравнения электромагнитного поля можно преобразовать к следующему виду:

Отметим, что электромагнитная волна называется плоской, когда векторы зависят только от одной координаты, например z.

Поляризованной называется такая волна, в которой вектор напряженности электрического поля все время остается параллельным некоторому направлению (например, как в нашем случае, оси ох), а вектор напряженности магнитного поля – другому (оси оy).

Такие условия обеспечиваются при излучении электромагнитных волн неподвижной антенной на достаточно большом расстоянии от нее.

Таким образом, в электромагнитной волне, свободно распространяющейся в однородном и изотропном диэлектрике, векторы взаимно перпендикулярны ().

Уравнения (4.1) и (4.2) можно преобразовать к следующему виду:

имеет размерность скорости.

Уравнение (4.3) является уравнением колебаний или волновым уравнением и относится к гиперболическому типу.

Как известно, решение такого уравнения всегда можно представить в виде:

При этом составляющая Е_х1 называется прямо бегущей или прямой волной (перемещается в положительную сторону оси oz со скоростью u), а составляющая Е_х2 – обратно бегущей или обратной волной (перемещается в отрицательную сторону оси oz со скоростью u).

Используя выражения (4.1), (4.2) и (4.4) получаем формулу для напряженности магнитного поля

Составляющие Н_х1 и Н_х2 также называют прямой и обратной волной.

Таким образом, электромагнитная волна распространяется в пространстве со скоростью u (в прямом или в обратном направлении).

В частности, в пустоте (m=m₀, e=e₀) эта скорость равна скорости света (u=2.998*10 8 м/с»3*10 8 м/с).

Если существует только прямая или только обратная волна, то энергии электрического и магнитного полей равны между собой, так как при этом равны их объемные плотности

Отношение Е_х1/Н_у1=?`m¤e=Z_в имеет размерность электрического сопротивления и называется волновым сопротивлением среды.

В частности, для пустоты Z_в=377Ом (Z_в =120p).

Таким образом, для любой среды

В случае, если прямая электромагнитная волна распространяется в среде, абсолютное значение магнитной проницаемости которой m=m₁, а абсолютное значение диэлектрической проницаемости e=e₁, и подходит нормально (перпендикулярно) к плоской границе, разделяющей данную среду и среду с m=m₂ и e=e₂, то прямая волна (Е_х1=Е_j₁, Н_х1=Н_j₁) частично будет проходить сквозь поверхность раздела, образуя во второй среде преломленную (прямую) волну (Е_j₂, Н_j₂), а частично будет отражаться от поверхности раздела, образуя в первой среде отраженную (обратную) волну (Е_х2=Е_y₁, Н_х2=Н_y₁).

Соотношение между напряженностями поля для этих волн на поверхности раздела можно представить следующим образом:

-соответствующие волновые сопротивления первой и второй среды.

Если волновые сопротивления сред равны между собой (Z_в1= Z_в2), то отраженные волны отсутствуют.

В случае, когда источник (антенна) излучает электромагнитную волну, в которой напряженность электрического и магнитного поля изменяется по гармоническому закону, то для прямой волны

Здесь y_н— начальная фаза; w – угловая частота колебаний (w=2pf).

Расстояние, на которое распространяется электромагнитная волна в течение одного периода колебаний Т (Т=1/f), называется длиной волны

Из данного выражения видно, что длина волны в диэлектрике обратно пропорциональна частоте f. Так, при частоте f=1 МГц длина волны в пустоте равна 300 м, а при f=50Гц l=6000 км.

Видео:Билет №34 "Электромагнитные волны"Скачать

ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ В СРЕДЕ

С ПРОВОДИМОСТЬЮ

3.6.1. Комплексная диэлектрическая проницаемость

1. Реальная среда в той или иной степени обладает проводимостью, т.к. в любой реальной среде содержится некоторое количество свободных зарядов. По проводимости среды делятся на проводники, полупроводники и диэлектрики. Вспомним курс общей физики. Энергетический спектр электронов в кристаллах имеет зонную структуру, и с позиции зонной теории проводимость сред количественно оценивается по энергетической ширине De последней запрещенной зоны (запрещенная зона находится между валентной зоной и зоной проводимости). Валентные электроны могут покидать свои атомы, если электроны приобретут достаточную энергию для преодоления потенциального барьера запрещенной зоны, и «принять участие» в электрическом токе.

В проводниках (например, в металлах) валентная зона и зона проводимости перекрываются, и валентные электроны в металлах уже при температурах близких к 0 К находятся в зоне проводимости. Металлы являются хорошими проводниками. Условно принято, что полупроводниками являются материалы, у которых ширина последней запрещенной зоны De 2 эВ. Однако, несмотря на довольно большую энергетическую ширину последней запрещенной зоны диэлектриков, статистически в межатомном пространстве реальных диэлектриков все же содержится некоторое количество свободных электронов, поэтому и диэлектрики обладают проводимостью, хотя и незначительной. Итак, соотношение между проводимостями диэлектриков g_д., полупроводников g_пп. и проводников g_пр можно выразить неравенством:

g_д. >ï ï, то такая среда является проводником, если ïgEï

Важно в приведенных оценочных неравенствах обратить внимание на то обстоятельство, что соотношение между током проводимости j и током смещения j_см зависит не только от параметров среды g и e, но и от быстроты изменения электрического поля электромагнитной волны — зависит также и от значения 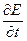, т.е. от частоты колебаний вектора E.

Допустим, электромагнитная волна является синусоидальной. Запишем уравнение Максвелла для ротора комплексной амплитуды H (раздел 3.4):

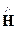
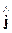
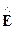
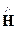
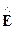
[Ñ,] = + или [Ñ,] = (g + ).

Последнее уравнение можно представить в виде:

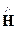
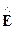
[Ñ,] = . (70)

e_к = 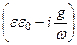(71)

называется комплексной диэлектрической проницаемостью.

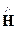
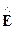
Итак, вместо уравнения [Ñ,] = + будем иметь уравнение

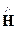
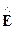
[Ñ,] = e_к . (72)

Уравнение (72) позволяет рассматривать любую среду как диэлектрик с комплексной диэлектрической проницаемостью e_к. Соотношение между вещественной частью ee₀ и мнимой 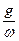комплексной диэлектрической проницаемости e_к определяет свойства среды:

— при g >> ee₀w среда является проводником;

— при g > w_гр.) основную роль играют токи смещения, и среда при этих частотах рассматривается как диэлектрик; при низких частотах волны (w

Например, проводимость меди g = 5,7×10 7 Сим/м, диэлектрическая проницаемость металлов того же порядка, что и диэлектрическая проницаемость воздуха e

(1 ¸ 10). Если принять e = 10, то имеем:

f_гр. = = = 10 17 Гц.

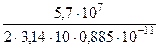
Полученная частота находится в ультрафиолетовом диапазоне электромагнитных волн (длина волны 3×10 -9 м). В радиодиапазоне (радиодиапазон простирается до частот 10 13 ¸10 14 Гц) металлы являются проводниками. Таким образом, в металлах в радиодиапазоне частот ток проводимости превышает ток смещения более чем в 10 3 раз. Для пресной воды (g = 10 -3 Сим/м, e = 81) граничная частота f_гр. = 2×10 5 Гц; для морской соляной воды (g = 4 Сим/м, e = 81) f_гр. = 10 9 Гц.

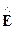
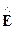
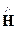
В нелинейных магнетиках (например, в ферромагнетиках) возможны магнитные потери и магнитная проницаемость становится комплексной величиной m_к, и уравнение для ротора вектора комплексной амплитуды запишется в виде: [Ñ,] = . (74)

В дальнейшем будем рассматривать линейные магнетики с постоянной магнитной проницаемостью и в отсутствии магнитных потерь в среде.

Умножив (72) и (74) на 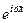, получим уравнения Максвелла для роторов комплексных функцийE_к и H_к в среде с проводимостью:

[Ñ, H_к] = e_к E_к, (75)

[Ñ, E_к] = H_к, (76)

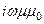
а также уравнения для дивергенций:

Ñ H_к = 0 и Ñ E_к = 0. (77)

3.6.2. Уравнение плоской волны в среде с проводимостью

Прежде чем рассматривать содержание данного параграфа, рекомендуем еще раз перечитать раздел 3.5, где приводятся волновые уравнения вещественных векторов E и H в идеальном диэлектрике и решения этих уравнений.

В идеальном диэлектрике волновое уравнение (40) получено из анализа уравнений Максвелла (26). Решением волновых уравнений являются уравнения волны (44*) и (45*), которые представим в комплексной форме, выделив отдельно множитель 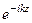, зависящий от координаты:

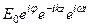
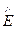
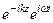
E_к = = ; (78)

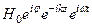
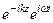
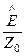
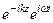
H_к = = = , (79)

где Z₀ = = , k = = . Так как фазовая скорость волны в диэлектрике определяется выражением v = , то волновое число можно записать в виде k = . Уравнения (78) и (79) описывают электромагнитную волну, распространяющуюся в положительном направлении оси 0Z, на это указывает знак минус в сомножителе .

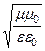
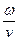
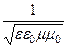
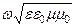
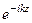
Среда с проводимостью. Структура уравнений Максвелла для комплексных функцийE_к и H_к в среде с проводимостью (75, 76, 77) одинакова со структурой системы уравнений Максвелла (26) в идеальном диэлектрике. Следовательно, решенияE_к и H_к в среде с проводимостью будут иметь вид, аналогичный уравнениям (78) и (79) с учетом того, что в среде с проводимостью диэлектрическая проницаемость e_к – комплексная величина. В решении волнового уравнения для среды с проводимостью вещественное волновое число k (вещественный фазовый множитель) следует заменить комплексной величиной — комплексным фазовым множителем, а вещественное волновое сопротивление Z₀ заменить комплексным волновым сопротивлением :

= = , где — комплексная фазовая скорость;

= = .

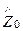
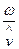
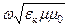
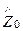
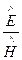
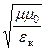
Запишем уравнения волны комплексных функцийнапряженности электрического поля E_к и напряженности магнитного поля H_к в среде с проводимостью E_к =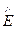 ; (80)

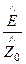
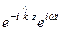
H_к = , (81)

Проведем анализ уравнений (80) и (81).

1. Комплексная величина , как любая комплексная величина, может быть представлена в виде:

= k — ia (82)

Подставим (82) в (80), получим:

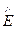
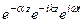
E_к = . (83)

Пусть начальная фазаEравна нулю, тогда это уравнение в тригонометрической форме имеет вид:

E_x = E₀ 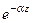cos (wt — kz) (83*)

(напомним, в этой записи принято, что плоская волна распространяется в положительном направлении оси 0Z, вектор E колеблется по оси 0X, вектор H — по оси 0Y).

Из (83) следует, что положительная величина a (мнимая часть комплексного фазового множителя ) определяет затухание амплитуды волны с расстоянием по мере удаления электромагнитной волны от источника волны и называется коэффициентом затухания. В экспериментальном плане a равна обратной величине некоторого расстояния l₀, на котором амплитуда волны E₀ уменьшается в e » 2,7 раз: a = . Ясно, что механизм потерь электромагнитной энергии в проводящей среде обусловлен возбуждением в среде электрических токов с последующим выделением джоулевого тепла.

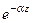
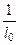
Величина k имеет тот же смысл волнового числа, что и в уравнении волны в идеальном диэлектрике: k = . Как и в идеальном диэлектрике, в среде с проводимостью волновое число k определяет фазовую скорость волны: v = . Фазовая скорость – это скорость распространения волновой поверхности (например, передней волновой поверхности — фронта волны).

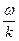
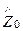
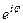
2. Комплексное волновое число представим в форме Эйлера (через экспоненту): =Z₀ . Здесь Z₀ — модуль, j — аргумент волнового сопротивления. Тогда уравнение волны для комплексной функции напряженности магнитного поля запишется как:

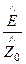
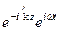
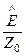
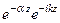
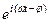
H_к = = . (84)

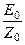
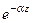
В обычной тригонометрической записи уравнение волны для напряженности магнитного поля электромагнитной волны в среде с проводимостью примет вид: H_y = cos (wt — kz — j). (85)

Из сравнения уравнений (83) и (85) следует, что в среде с проводимостью имеется сдвиг фаз между электрическим и магнитным полями электромагнитной волны. Напомним, в идеальном диэлектрике фазовый сдвиг между векторами E и H отсутствует (§3.5.2).

Воспользовавшись соотношениями для комплексного фазового множителя и комплексного волнового сопротивления

= = k — ia и = = Z₀ , где e_к = ,

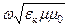
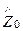
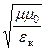
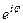
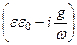
можно получить оценочные формулы для вещественных величин: коэффициента затухания a; вещественного фазового множителя k; фазовой скорости v; модуля аргумента волнового сопротивления Z₀; сдвига фаз j между E и H. Вывод основывается на возведение в квадрат первого соотношения и последующего приравнивания действительной и мнимой частей полученного равенства. Вывод оценочных формул несложный, и подробности вывода здесь опустим. Приведем результаты для двух случаев.

А. Среда — реальный диэлектрик (ee₀w >> g — среда обладает незначительной проводимостью):

— волновое сопротивление: Z₀ = »

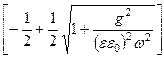
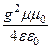
— коэффициент затухания: a 2 = wee₀mm₀» или

a » = ;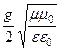

— фазовой множитель: k = wee₀mm₀» ;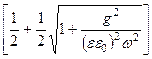

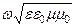
— фазовая скорость волны: v = = » ;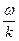

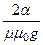
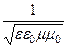
— сдвиг фазы между E и H: j = arctg 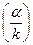» 0.

Из приведенных оценок следует, что в реальном диэлектрике с незначительной проводимостью результаты такие же, что и в идеальном диэлектрике. В реальном диэлектрике коэффициент затухания a не зависит от частоты, а определяется проводимостью g и волновым сопротивлением Z₀.

Б. Среда — проводник. С учетом соотношения для хорошо проводящей среды g >> ee₀w , получим:

— волновое сопротивление: Z₀ » ;

— коэффициент затухания: a » ;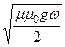

— фазовой множитель: k » ;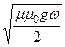

— фазовая скорость волны: v » ;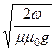

— сдвиг фазы между E и H: j = arctg » .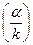

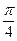
Из полученных оценок следует, что в проводящей среде:

1) происходит поглощение энергии электромагнитной волны, и это поглощение можно характеризовать коэффициентом затухания амплитуды волны в проводящей среде, причем в проводниках a » k (напомним, в курсе общей физики было показано, что энергия электромагнитной волны определяется квадратом амплитудыE и H). Например, в меди при обычной радиотехнической частоте f = 100 МГц (длина волны 3 м) a » 15×10 4 м — 1 , следовательно, при прохождении волной расстояния l₀ = » 7×10 — 6 м = 7×10 — 3 мм амплитуда в проводящей среде уменьшается в e = 2,7 раз;

2) фазовая скорость v очень мала. Например, в меди v » 4×10 2 м/с (сравните, в вакууме v » 3×10 8 м/с);

3) волновое сопротивление Z₀ проводников очень мало. Например, волновое сопротивление меди » 4×10 — 3 Ом (сравните, волновое сопротивление вакуума » 380 Ом). Уже из этого следует, что в проводящей среде перенос энергии осуществляется в основном магнитным полем электромагнитной волны (см. определение волнового сопротивления). Приведем оценку данного эффекта, для чего сравним максимальную плотность энергии магнитного и электрического поля электромагнитной волны в проводящей среде:

= = = .

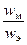
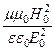
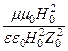
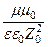
Например, для меди » 3×10 7 , т.е. практически вся энергия электромагнитного поля в проводнике сосредоточена в магнитном поле (при вычислении принято, что магнитная проницаемость m и диэлектрическая проницаемость порядка металлов порядка проницаемости воздуха, т.е.

4) в проводниках фазы колебаний векторов E и Hне совпадают.

Видео:Раскрытие тайн электромагнитной волныСкачать

Курс I. Уравнения Максвелла в диэлектрической среде

Уравнения Максвелла в диэлектрической среде

Уравнения Максвелла в произвольной среде таковы

(1a)

система (1a) замыкается материальными соотношениями . Здесь — векторы электрической и магнитной индукции; — плотность токов проводимости; — плотность электрических зарядов; — величины, характеризующие свойства среды и считающиеся при этом заданными функциями точки, но не времени; — сторонние электродвижущие силы – заданные функции точки и времени.

Заметим, что в приведенном, общепринятом виде (1a) формулировка уравнений принадлежит Герцу (Максвелл уравнения приводил в интегральной форме).

Заметим также, что система (1a) – это постулат, обобщающий все известные до Максвелла явления электричества и магнетизма (Кулон 1785 г. – закон взаимодействия электрических зарядов; Эрстед 1820 г. – магнитное действие тока, существование связи между магнитными и электрическими явлениями; Ампер – все магнитные явления в природе вызваны электрическими токами (теория молекулярных токов Ампера); Фарадей 1831 г. – электромагнитная индукция; и т. д.)

Волновое уравнение. Электромагнитная природа света.

Для интересующих нас в дальнейшем диэлектриков с , система Максвелла принимает вид

(1.1)

откуда, если диэлектрическая проницаемость не зависит от времени, получаем

(1.2)

Из векторного анализа известно

тогда (1.2) принимает вид

(1.3)

Далее, из условия находим

, (1.4)

В результате, вместо (1.3) имеем

(1.5)

Аналогично, для найдем

(1.6)

В случае однородных диэлектриков , и (1.5),(1.6) принимают вид

(1.7)

Уравнения (1.7) называются волновыми. Их справедливость ограничена лишь требованием однородности среды и отсутствия в ней токов проводимости и свободных зарядов.

К ним относятся как граничные условия на поверхностях разделов сред, так и условия на границах рассматриваемой области пространства. Последние полностью определяются конкретными условиями задачи (например, условия на бесконечности).

Условия на границах разделов для диэлектриков (отсутствие поверхностных зарядов и токов проводимости) эквивалентны уравнениям

, , (1.8)

где индексы 1 и 2 относятся к двум граничащим средам, а t означает любое направление, касательное к поверхности раздела.

Плоские электромагнитные волны

Одним из простейших решений волнового уравнения является плоская волна.

Волна называется плоской, если в любой момент времени во всех точках произвольной плоскости, перпендикулярной направлению распространения волны, векторы поля постоянны. Если этим направлением считать ось z, то компоненты поля плоской, монохроматической волны имеют вид

, , (1.9)

где — частота; векторы , вообще говоря, комплексные и зависят только от координаты z.

Подстановка (1.9) в волновые уравнения (1.7) дает

, , (1.10)

где — волновое число в диэлектрике.

Элементарно решив (1.10), найдем решения волновых уравнений в случае плоских волн в виде

, , (1.11)

каждое из которых представляет собой суперпозицию двух волн, распространяющихся в противоположных направлениях оси z. Здесь — произвольные постоянные интегрирования.

Обычно, в качестве решения рассматривается одна из волн, например,

, . (1.12)

С помощью найденного простейшего решения (1.12) можно продемонстрировать ряд важнейших общих свойств электромагнитных волн.

В частности, если ось z координатной системы не совпадает с направлением распространения волны, дифференцирование векторов поля по координатам сведется к их умножению на величину , где — единичный вектор в направлении распространения. Для однородных диэлектриков из уравнений Максвелла имеем

, , (1.13)

откуда следует, что векторы и перпендикулярны к , т. е. плоские электромагнитные волны – суть поперечные волны.

По аналогии, дифференцирование векторов поля по t сводится к их умножению на . В частности, из второго уравнения Максвелла (1.1) получаем

или, с учетом ,

. (1.14)

Последнее означает, что векторы и взаимно перпендикулярны, а три взаимно перпендикулярных вектора , и образуют правовинтовую систему.

Из (1.14) следует также, что , т. е. отношение числовых значений векторов и от времени не зависит, т. е. эти векторы обладают одинаковыми фазами и изменяются синхронно.

Всегда следует помнить, что физический смысл компонент поля, записанных в комплексной форме (см., например, запись (1.12)), несут лишь действительные части этих выражений. При этом каждая из декартовых компонент электрического и магнитного векторов поля плоской, монохроматической волны имеет вид

a>0. (1.15)

Здесь обозначает переменную часть фазового множителя, т. е.

, (1.16)

— направление распространения волны; — постоянная часть этого множителя.

Совместим ось z c . Тогда, в силу поперечности волны отличными от нуля будут только x — и y-компоненты векторов. Исследуем характер кривой, которую конец электрического (или магнитного) вектора описывает в произвольной точке пространства. Эта кривая – геометрическое место точек с координатами

(1.17)

a) Эллиптическая поляризация

После несложных математических операций исключим из (1.17) и получим

, (1.18)

где .

В аналитической геометрии показывается, что (1.18) представляет собой уравнение конического сечения, а более конкретно – уравнение эллипса. Этот эллипс вписан в прямоугольник, стороны которого параллельны координатным осям и имеют длины и . Таким образом, конец электрического вектора описывает эллипс в любой плоскости, перпендикулярной направлению распространения.

Аналогично показывается, что конец магнитного вектора поля также описывает эллипс, вписанный в прямоугольник со сторонами в раз большими. Последнее следует, в частности, из соотношения (1.14).

Из общих физических соображений следует также различать две возможные эллиптические поляризации в соответствии с направлением, в котором конец электрического вектора описывает эллипс. В литературе сформировалось определение, согласно которому правой поляризация называется, когда наблюдателю, смотрящему навстречу световому лучу, кажется, что конец электрического вектора движется по часовой стрелке. Для левой эллиптической поляризации справедливо обратное.

Поскольку параметры в предыдущем рассмотрении были произвольными, то эллиптическую поляризацию электромагнитных волн следует считать наиболее общим из состояний поляризации. Более частные типы поляризации соответствуют определенным соотношениям между этими параметрами.

b) Линейная и круговая поляризации

Перейдем к рассмотрению частных случаев.

то эллипс (1.18) превратится в прямую линию. В самом деле, уравнение (1.18) переходит при этом в

, (1.19)

а конец электрического вектора в прямоугольнике колеблется вдоль одной из его диагоналей.

Иногда эта линейная поляризация называется еще плоской поляризацией. Понятно, что в этой ситуации магнитный вектор также линейно поляризован.

Другим частным случаем эллиптической поляризации является круговая. Переход от эллиптической к круговой поляризации происходит тогда, когда, во-первых, и, во-вторых,

, .

Уравнение (1.18) переходит при этом в уравнение окружности

, (1.20)

где также различают правую и левую поляризации.

Круговая поляризация иногда называется циркулярной.

Итак, во всех случаях поляризованного света концы векторов поля в каждой точке движутся периодически. В случае же неполяризованного света они движутся совершенно нерегулярно, и такие световые колебания не имеют никаких преимущественных направлений в плоскости, перпендикулярной направлению распространения.

Основные законы оптики – преломление света, отражение, полное внутреннее

Применим теперь найденные выше для плоских волн соотношения к исследованию распространения этих волн при наличии плоской границы, разделяющей два однородных, изотропных диэлектрика, занимающих два полупространства.

В задаче о преломлении волн на границе полубесконечной среды физический смысл имеет решение, основанное на предположении о наличии трех волн: падающей, отраженной и преломленной.

Падающая на границу волна порождает новый волновой процесс.

По определению плоская волна полностью определена, если известно ее поведение во времени в некоторой точке пространства. Вторичные поля, возникающие на границе, будут так же изменяться во времени, как и первичное поле падающей волны. Поэтому переменные части фазовых множителей трех волн в произвольной точке должны быть одинаковыми:

, (1.21)

где — единичные векторы в направлениях падающей, отраженной и преломленной волн; — скорости распростра

нения волн в обеих средах.

Выбрав в качестве границы раздела плоскость z=0, (1.21) запишем в виде

. (1.22)

Равенства должны выполняться для любых значений x и y на границе. Это дает

(1.23)

откуда следует, что все три вектора лежат в одной плоскости с нормалью к границе (в плоскости падения).

Выберем в качестве плоскости падения плоскость xz. Тогда y-компоненты векторов равны нулю, а прочие таковы:

(1.24)

где — углы, которые образуют с осью z (рис. 1).

Из (1.24) и (1.23) имеем

(1.25)

откуда , и из рис. 1 видно, что , т. е. угол падения равен углу отражения. В этом состоит закон отражения.

Из (1.25) следует также

(1.26)

Последнее соотношение вместе с утверждением, что нормаль к преломленной волне лежит в плоскости падения составляет закон преломления (или закон Снеллиуса).

Если > (луч падает из более плотной в менее оптически плотную среду), то из (1.26) видно, что для любого угла падения существует вещественный угол преломления ( воспользуемся им и положим

Тогда (1.27) примет вид

(1.28)

Ясно также, что физический смысл имеет лишь нижний знак перед корнем во втором сомножителе в (1.28).

Из (1.28) следует, и это подтверждается опытным путем, что электромагнитное поле в среде 2 все же не равно нулю. Волна (1.28) представляет собой неоднородную волну, распространяющуюся в плоскости падения вдоль x по поверхности раздела сред и с экспоненциально падающей с ростом z амплитудой. Эта волна не является поперечной, поскольку ее компонента электрического вектора . Эффективная глубина ее проникновения в обе стороны от поверхности раздела сред оказывается порядка длины волны.