Уравнение плоскости xoz в пространстве (3 видео)

Общее уравнение плоскости

В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн.

Пусть задана произвольная декартова прямоугольная система координат Oxyz. Общим уравнением плоскости называется линейное уравнение вида:

Ax+By+Cz+D=0,

(1)

где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля.

Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.

Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть в пространстве задана плоскость α. Выберем оси Ox и Oy так, чтобы они располагались на плоскости α, а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z=0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z=0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.

Пусть фиксирована произвольная декартова прямоугольная система координат Oxyz. Рассмотрим линейное уравнение (1), где хотя бы один из элементов A , B и C отлично от нуля. Тогда уравнение (1) имеет хотя бы одно решение x₀, y₀, z₀. Действительно. Пусть из коэффициентов A≠0. Возьмем произвольные числа y₀, z₀. Тогда

Таким образом, существует точка M₀(x₀, y₀, z₀), координаты которой удовлетворяют уравнению (1):

Ax₀+By₀+Cz₀+D=0.

(2)

Вычитая из уравнения (1) тождество (2), получим

A(x−x₀)+B(y−y₀)+С(z−z₀)=0,

(3)

которая эквивалентна уравнению (1).

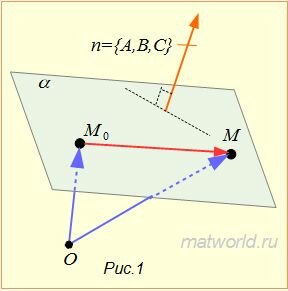Покажем, что (3) определяет некоторую плоскость, проходящую через точку M₀(x₀, y₀, z₀) и перпендикулярную вектору n=<A,B,C> (n≠0, так как хотя бы один из чисел A,B,C отлично от нуля).

Если точка M₀(x₀, y₀, z₀) принадлежит плоскости α, то ее координаты удовлетворяют уравнению (3), т.к. векторы n=<A,B,C> и перпендикулярны (Рис.1) и их скалярное произведение равно нулю:

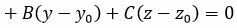Если же точка M(x, y, z) не лежит на плоскости α, то векторы n=<A,B,C> и не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.

Одновременно с доказательством теоремы 1 мы получили следующее утверждение.

Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C) перпендикулярен плоскости Ax+By+Cz+D=0.

Вектор n=(A,B,C) называется нормальным вектором плоскости , определяемой линейным уравнением (1).

Утверждение 2. Если два общих уравнения плоскости

A₁x+B₁y+C₁z+D=0

(4)

A₂x+B₂y+C₂z+D=0

(5)

определяют одну и ту же плоскость, то найдется такое число λ, что выпонены равенства

A₂=A₁λ, B₂=B₁λ, C₂=C₁λ, D₂=D₁λ.

(6)

A₁x₀+B₁y₀+C₁z₀+D=0

(7)

A₂x₀+B₂y₀+C₂z₀+D=0

(8)

Умножая уравнение (7) на λ и вычитая из него уравнение (8) получим:

(A₁λ−A₂)x₀+(B₁λ−B₂)y₀+(C₁λ−C₂)z₀+(D₁λ−D₂)=0.

Так как выполнены первые три равенства из выражений (6), то D₁λ−D₂=0. Т.е. D₂=D₁λ. Утверждение доказано.

Содержание

Неполные уравнения плоскости
1.2.2. Общее уравнение плоскости. Неполное уравнение
Некоторые простые уравнения. Уравнения координатных плоскостей
Уравнения координатных плоскостей
Уравнение плоскости, параллельной
Некоторые простые уравнения координатной плоскости.
💡 Видео

Видео:Уравнение плоскости. 11 класс.Скачать

Неполные уравнения плоскости

Определение 1. Общее уравнение плоскости (1) называется полным , если все коэффициенты A, B, C, D отличны от нуля. Если же хотя бы один из коэффициентов A, B, C, D равен нулю, то общее уравнение плоскости называется неполным .

Рассмотрим все возможные варианты неполных уравнений плоскости:

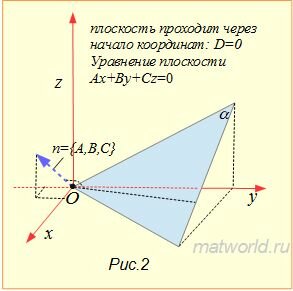
При D=0, имеем уравнение плоскости Ax+By+Cz=0, проходящей через начало координат (Рис.2). Действительно, точка O(0,0,0) удовлетворяет этой системы линейных уравнений.

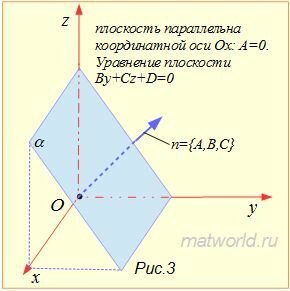
При A=0, имеем уравнение плоскости By+Cz+D=0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n=<0,B,C> лежит на координатной плоскости Oyz.

При B=0, имеем уравнение плоскости Ax+Cz+D=0, которая параллельна оси Oy (Рис.4).

При C=0, имеем уравнение плоскости Ax+By+D=0, которая параллельна оси Oz (Рис.5).

При A=0,B=0 имеем уравнение плоскости Cz+D=0, которая параллельна координатной плоскости Oxy (Рис.6).

При B=0,C=0 имеем уравнение плоскости Ax+D=0, которая параллельна координатной плоскости Oyz (Рис.7).

При A=0,C=0 имеем уравнение плоскости By+D=0, которая параллельна координатной плоскости Oxz (Рис.8).

При A=0,B=0,D=0 имеем уравнение плоскости Cz=0, которая совпадает с координатной плоскостью Oxy (Рис.9).

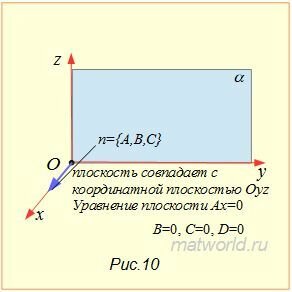
При B=0,C=0,D=0 имеем уравнение плоскости Ax=0, которая совпадает с координатной плоскостью Oyz (Рис.10).

При A=0,C=0,D=0 имеем уравнение плоскости By=0, которая совпадает с координатной плоскостью Oxz (Рис.11).

Рассмотрим примеры построения общего уравнения плоскости.

Пример 1. Построить общее уравнение плоскости, проходящей через точку M(4,−1,2) параллельной координатной плоскости Oxy.

Решение. Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя координаты точки M в (3), получим:

A(x−4)+B(y−(−1))+C(z−2)=0

(9)

Так как плоскость параллельна координатной плоскости Oxy, то направляющий вектор имеет следующий вид n=<A,B,C>=, т.е. A=0, B=0, C=1.

Подставляя коэффициенты A,B,C в (9), получим:

0(x−4)+0(y−(−1))+1(z−2)=0

(9)

Пример 2. Построить общее уравнение плоскости, проходящей через начало координат и имеющий нормальный вектор n==.

Решение. Начало координат имеет коэффициенты (0,0,0). Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя коэффициенты начальной точки в (3), получим:

A(x−0)+B(y−0)+C(z−0)=0

(10)

Так как плоскость имеет нормальный вектор n=<A,B,C>=, т.е. A=2, B=3, C=1, подставляя коэффициенты A,B,C в (10), получим:

2(x−0)+3(y−0)+1(z−0)=0

(9)

Онлайн калькулятор для построения общего уравнения плоскости находится здесь. Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

1.2.2. Общее уравнение плоскости. Неполное уравнение

Раскрывая скобки и обозначая свободный член – Ax0 – By0 – Cz0 = D, получим общее уравнение плоскости В пространстве R3:

Ax+By+Cz+D=0, A2+B2+C2>0. (4)

Итак, линейное относительно текущих координат x, y,z уравнение (4) определяет плоскость в пространстве (причем, =(A, B,C) ее нормаль). Можно показать, что верно и обратное утверждение: всякое линейное уравнение (4) в пространстве R3 определяет некоторую плоскость.

Пример. Написать уравнения координатных плоскостей.

Для того, чтобы написать уравнение любой плоскости надо знать координаты какой-нибудь точки на плоскости и какой-нибудь вектор, перпендикулярный плоскости.

В нашем примере все координатные плоскости проходят через точку M0(0,0,0) – начало координат.

А в качестве нормалей к координатным плоскостям можно взять соответственно базисные векторы .

Плоскость XOY: М0(0,0,0), (0,0,1)=(A, B,C).

0(x – 0) + 0(y – 0) + 1(z – 0)=0

Уравнение плоскости XOY: z=0.

Плоскость YOZ: M0(0,0,0), :

Уравнение плоскости YOZ: x=0.

Плоскость XOZ: M0(0,0,0), :

Уравнение плоскости XOZ: y=0.

Заметим, что в нашем примере в уравнениях координатных плоскостей отсутствуют два члена с текущими координатами (какие-либо два из коэффициентов A, B,C равны нулю).

Уравнение плоскости (4), в котором хотя бы один из коэффициентов A, B,C или D равен нулю, называют Неполным уравнением плоскости. В этих случаях плоскость либо параллельна одной из координатных осей (один из коэффициентов A, B,C равен нулю, или, что то же, вектор нормали ортогонален одной из координатных осей); либо плоскость (4) параллельна одной из координатных плоскостей (два из коэффициентов A, B,C равны нулю, параллелен какой-нибудь координатной оси); если же коэффициент D уравнения (4) равен нулю, т. е. точка (0,0,0) удовлетворяет уравнению плоскости, плоскость проходит через начало координат.

Видео:Лекция 25. Виды уравнений плоскости в пространстве.Скачать

Некоторые простые уравнения. Уравнения координатных плоскостей

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Уравнения координатных плоскостей

Рассмотрим, например, плоскость хОу и произвольную точку М на ней. Так как плоскость хОу J_ Oz, то перпендикуляр, опущенный из точки М на ось Oz, попадает в начало координат, а это значит, что аппликата точки равна нулю. Очевидно и обратное, т. е. если аппликата точки равна нулю, то эта точка лежит в плоскости хОу.

Поэтому уравнение z = О характеризует плоскость хОу оно является уравнением плоскости хОуу т. е. координаты любой точки плоскости хОу удовлетворяют уравнению z — 0. Рассуждая аналогично, получим, что координаты любой точки, принадлежащей плоскости xOz> удовлетворяют уравнению .у = 0, т. е. это уравнение есть уравнение координатной плоскости xOz. Также уравнение л; = 0 есть уравнение координатной плоскости yOz. 2.

Уравнение плоскости, параллельной

Некоторые простые уравнения координатной плоскости.

Возможно вам будут полезны данные страницы:

Если точка М лежит в плоскости, параллельной плоскости хОу, то ее аппликата равна расстоянию точки от плоскости хОу, взятому со знаком плюс, если точка лежит выше, и со знаком минус, если она лежит ниже координатной плоскости хОу. Поэтому уравнение плоскости, параллельной координатной плоскости хОу, имеет вид z = с, где с — постоянное. Также плоскость, параллельная плоскости xOzy имеет уравнение у = Ь. Плоскость, параллельная плоскости yOz, имеет уравнение х

Уравнения координатных осей.

Ось Oz является пересечением плоскости xOz и плоскости yOz, поэтому любая ее точка лежит в плоскости xOz и в плоскости yOz. Следовательно, координаты любой точки, принадлежащей оси Oz, должны удовлетворять и уравнению у — 0 и уравнению х = 0. Эти два уравнения л: = 0 и у = 0 являются уравнениями оси Oz. Аналогично уравнениями оси Оу будут jc = 0, z=^0. Уравнениями оси Ох будут у = О, z =

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.