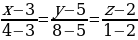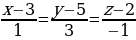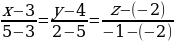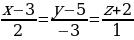Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Практическая работа по теме «Уравнение плоскости»
Цель: развитие практических навыков составления уравнений плоскости по различным условиям.
Время выполнения : 90 мин.
Составить уравнение плоскости, которая проходит через точку М(-5; 1; 1) и имеет нормальный вектор n=.
Составить уравнение плоскости, проходящей через точку D (3;-1;2) и параллельной векторам .
Составить уравнение плоскости, проходящей через точки M 1 (-4; -1; -3), M 2 (-1; 5; 2) параллельно вектору =.
Составить уравнение плоскости, проходящей через точки A (1;2;3), B (-1;3;5), C (2;0;4).
Составить уравнение плоскости, которая проходит через точку М(-2; 3; -2) перпендикулярно к двум плоскостям , .
Составить уравнение плоскости, которая проходит через две точки М 1 (-3; -1; 2),
M 2 (-3; 4; -5) перпендикулярно к плоскости .
Найти расстояние от точки до плоскости .
Выясните взаимное расположение плоскостей:
Найдите расстояние между параллельными плоскостями:
Найдите косинус угла между плоскостями:
Что является расстоянием между параллельными плоскостями?
Чем отличается нормальный вектор от направляющего вектора?
Для отчёта представить:
Решение индивидуального задания.
Письменные ответы на контрольные вопросы.
«5» — выполнено 90-100% всех заданий;
«4» — выполнено 70-90% всех заданий;
«3» — выполнено 50-70% всех заданий;
«2» — выполнено менее 50% всех заданий.
- Краткое описание документа:
- Дистанционное обучение как современный формат преподавания
- Математика: теория и методика преподавания в образовательной организации
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Дистанционные курсы для педагогов
- Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
- Материал подходит для УМК
- Другие материалы
- Вам будут интересны эти курсы:
- Оставьте свой комментарий
- Автор материала
- Дистанционные курсы для педагогов
- Подарочные сертификаты
- Уравнение плоскости в пространстве
- Уравнение прямой, плоскости и сферы
- Просмотр содержимого документа «Уравнение прямой, плоскости и сферы»
- 💥 Видео
Краткое описание документа:
Практическая работа по теме «Уравнение плоскости» предназначена для отработки практических навыков по теме. Она содержит типовые задания для нахождения уравнения плоскости при различных условиях.
При необходимости можно увеличить количество вариантов, изменив численные условия в задачах.
Работа может использоваться для уроков геометрии для школьников, а также для студентов средних учебных заведений по разделу математики «Аналитическая геометрия»
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 945 человек из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 687 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 315 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Видео:Лекция 25. Виды уравнений плоскости в пространстве.Скачать
Дистанционные курсы для педагогов
«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»
Свидетельство и скидка на обучение каждому участнику
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 592 994 материала в базе
Материал подходит для УМК
«Математика: алгебра и начала математического анализа, геометрия. Геометрия (базовый и углубленный уровни)», Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др.
3.2. Свойства параллельных плоскостей
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»
Свидетельство и скидка на обучение каждому участнику
Другие материалы
- 21.01.2018
- 1276
- 10
- 20.01.2018
- 8645
- 46
- 20.01.2018
- 1137
- 18
- 19.01.2018
- 2410
- 39
- 18.01.2018
- 2346
- 23
- 17.01.2018
- 2267
- 26
- 15.01.2018
- 389
- 3
- 14.01.2018
- 444
- 0
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 22.01.2018 3009
- DOCX 14.5 кбайт
- 126 скачиваний
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Тюрикова Татьяна Леонидовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 1 месяц
- Подписчики: 0
- Всего просмотров: 23199
- Всего материалов: 5
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Видео:Уравнение плоскости. 11 класс.Скачать
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной
Время чтения: 0 минут
Минобрнауки создаст для вузов рекомендации по поддержке молодых семей
Время чтения: 1 минута
В приграничных пунктах Брянской области на день приостановили занятия в школах
Время чтения: 0 минут
Минпросвещения упростит процедуру подачи документов в детский сад
Время чтения: 1 минута
Курские власти перевели на дистант школьников в районах на границе с Украиной
Время чтения: 1 минута
Школьник из Сочи выиграл международный турнир по шахматам в Сербии
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать
Уравнение плоскости в пространстве
Оглавление
Варианты контрольной работы №2………………………………………………….2
Справочный материал по теме«Аналитическая геометрия на плоскости……….3
1. Декартова система координат (ДСК) на плоскости………………….……. 3
2. Прямая линия на плоскости……………………………………………………3
Справочный материал по теме «Аналитическая геометрия в пространстве»……4
1. Уравнение плоскости в пространстве…………………………….……. 4
2. Уравнения прямой в пространстве…………………………………..………..5
Примерный вариант и образец выполнения домашней контрольной №2………. 6
Варианты контрольной работы №2
Задача 1. Даны координаты вершин треугольника АВС.
| № варианта | Координаты точек | № варианта | Координаты точек |
| А(–2; –3), В(2; 7), С(6; –1) | А(3; –3), В(–4; 1), С(–2; 5) | ||
| А(–5; 1), В(6; 3), С(–4; –7) | А(3; 5), В(–2; 2), С(2; –4) | ||
| А(4; 5), В(–3; 2), С(5; –4) | А(–2; 4), В(5; 6), С(3; –4) | ||
| А(7; –7), В(1; 2), С(–5; –4) | А(3; 7), В(–4; 1), С(–2; –5) | ||
| А(–2; –3), В(6; 3), С(5; –4) | А(3; 5), В(5; 6), С(3; –4) | ||
| А(–3; 4), В(4; 5), С(8; –3) | А(4; 3), В(–3; –2), С(–7; 2) |
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) найти внутренний угол треугольника при вершине В;
4) составить уравнение высоты АК, проведенной из вершины А;
5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);
6) сделать чертеж в системе координат.
Задача 2. Даны координаты точек – вершин пирамиды ABCD.
| № варианта | Координаты точек |
| А(1; 2; –1), В(0; 0; 1), С(1; –3; 3), D(2; –1; –1) | |
| А(7; 2; 4), В(7; –1; –2), С(3; 3; 1), D(4; 2; 1) | |
| А(1; 3; 6), В(2; 2; 1), С(–1; 0; 1), D(–4; 6; –3) | |
| А(–2; 0; –4), В(–1; 7; 1), С(4; –8; –4), D(1; –4; 6) | |
| А(1; 2; 0), В(3; 0; –1), С(5; –2; 3), D(3; 2; –1) | |
| А(–1; 1; 2), В(2; 1; –2), С(–2; 0; 4), D(2; –1; 2) | |
| А(4; 2; 5), В(2; –3; 0), С(–10; 5; 8), D(–5; 2; 4) | |
| А(2; –1; 1), В(–1; –3; 2), С(–2; 3; 1), D(–1; 2; –3) | |
| А(7; 2; 4), В(2; 2; 1), С(4; –8; –4), D(3; 2; –1) | |
| А(–1; 1; 2), В(2; –3; 0), С(–10; 5; 8), D(–2; 1; –1) | |
| А(–1; 1; 2), В(–2; 0; 3), С(3; 6; –3), D(–1; –2; 7) | |
| А(4; –1; 3), В(–2; 1; 0), С(0; –5; 1), D(–2; 1; –1) |
1) вычислить длину ребра AB;
2) найти уравнение плоскости грани ABC;
3) найти угол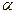 
между гранями ABC и BCD;
4) составить параметрические уравнения прямой AB;
5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;
6) найти координаты точки пересечения DK и грани ABC;
7) найти угол 
между ребрами AB и BC;
8) найти угол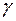 
между ребром AD и гранью ABC;
9) сделать чертеж пирамиды в системе координат.
Справочный материал по теме «Аналитическая геометрия на плоскости» (задачА 1)
Декартова система координат (ДСК) на плоскости
|AB| =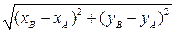 
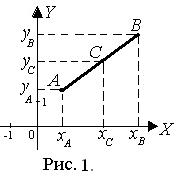
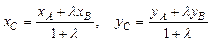
. (1)
Деление отрезка в заданном отношении. Если точка С делит отрезок АВ в отношении λ, начиная от точки A (рис. 1), т.е. 
, то координаты точки C:
. (2)
Если точка С делит отрезок АВ пополам, т.е. 
=1, то координаты точки C:
. (3)
В ДСК уравнение линии имеет вид F(х, у) = 0 или у = f(х).
Прямая линия на плоскости
Общее уравнение прямой на плоскости:
Уравнение прямой с угловым коэффициентом (рис. 3):
Уравнение вертикальной прямой (рис. 2):
Уравнения прямых, проходящих через одну заданную точку М(х0; у0) (уравнение пучка прямых):
у – y0 = k(x – x0). (6)
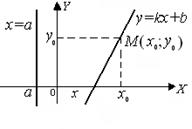
Рис.2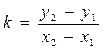 
. (7)
Уравнение прямой, проходящей через две заданные точки:
. (8)
Пусть на плоскости заданы две прямые, которым соответствуют уравнения с угловыми коэффициентами: у = k1 x + b1 и у = k2 x + b2.
Условие параллельности прямых на плоскости:
Условие перпендикулярности прямых:
. (10)
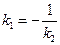
Если одна из двух перпендикулярных прямых вертикальная, т.е. k2 не существует, то k1= 0 и обратно: если k2 = 0, то k1 не существует.
Тангенс острого угла между пересекающимися прямыми можно найти, используя формулу:
, (11)
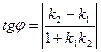
откуда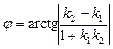 
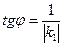
. Если одна из прямых вертикальная, т.е. k2 не существует, то 
.
Справочный материал по теме «Аналитическая геометрия В ПРОСТРАНСТВЕ» (задачА 2)
Уравнение плоскости в пространстве
Общее уравнение плоскости: 
,
где A, B, C – координаты вектора нормали вектора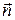 
(любого вектора, перпендикулярного данной плоскости), D – свободный член уравнения.
Уравнение плоскости, проходящей через точку 
перпендикулярно вектору 
:
. (12)
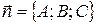
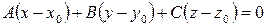
Уравнение плоскости, проходящей через три заданные точки 
:
. (13)
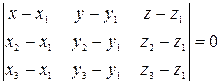
Угол 
между двумя плоскостями, заданными уравнениями 
и 
определяется как угол между векторами их нормалей 
и 
или дополнительный к нему (обычно берется острый угол), то есть
. (14)
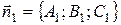
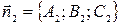
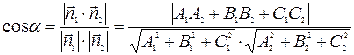
Видео:Видеоурок "Уравнение плоскости в отрезках"Скачать
Уравнение прямой, плоскости и сферы
306 гр. Математика. Дистанционное обучение. Тема 1-3.
Просмотр содержимого документа
«Уравнение прямой, плоскости и сферы»
Тема 1: Уравнение прямой в пространстве.
З 
адание: записать конспект и выполнить самостоятельную работу.
Пример 1. Составить уравнение прямой, проходящей через две точки:
Подставив в уравнение прямой соответствующие координаты, получим:
Упростим: 
Ответ:
Пример 2. Составить уравнение прямой, проходящей через две точки:
Подставив в уравнение прямой соответствующие координаты, получим:
Упростим: 
Ответ: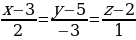 
Самостоятельная работа
Пример 1. Составить уравнение прямой, проходящей через две точки:
Пример 2. Составить уравнение прямой, проходящей через две точки:
Пример 3. Составить уравнение прямой, проходящей через две точки:
Тема 2: Уравнение плоскости в пространстве
Задание: записать конспект и выполнить самостоятельную работу
П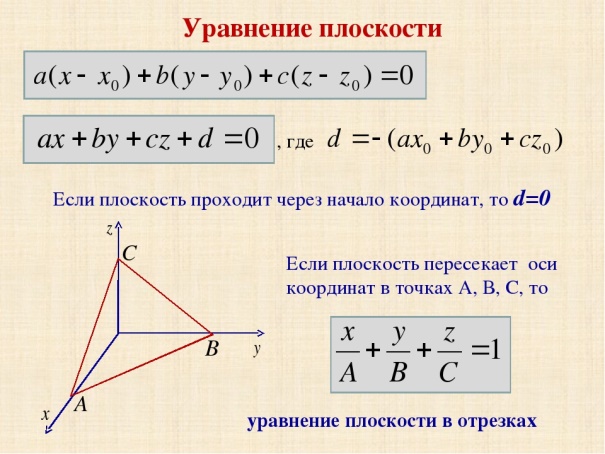 
ример 1: Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0
Решение: Подставим координаты точки в уравнение и проверим верно ли равенство.
Ответ: точка В (-1; 2; 7) принадлежит плоскости.
Пример 2: Принадлежит, ли точка Е(0; 4; -6) плоскости, заданной уравнением х-5у-4z+2=0
Решение: Подставим координаты точки в уравнение и проверим верно ли равенство. х-5у-4z+2=0
0-5·4-4·(-6)+2=0-20+24+2=6≠0 не верно
Ответ: точка Е(0; 4; -6) не принадлежит плоскости.
Пример 3: При каком D точка А(1; 5;-2) принадлежит плоскости -3х+2у-z+D=0
Решение: Подставим координаты точки в уравнение и найдем D.
Пример 1: Принадлежит, ли точка В (-2; 3; 8) плоскости, заданной уравнением
Пример 2: Принадлежит, ли точка Е(3; 4; -2) плоскости, заданной уравнением
Пример 3: При каком D точка А(2; 4;-1) принадлежит плоскости -2х+5у-z+D=0
Решить задания №1, №2
О 
пределение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.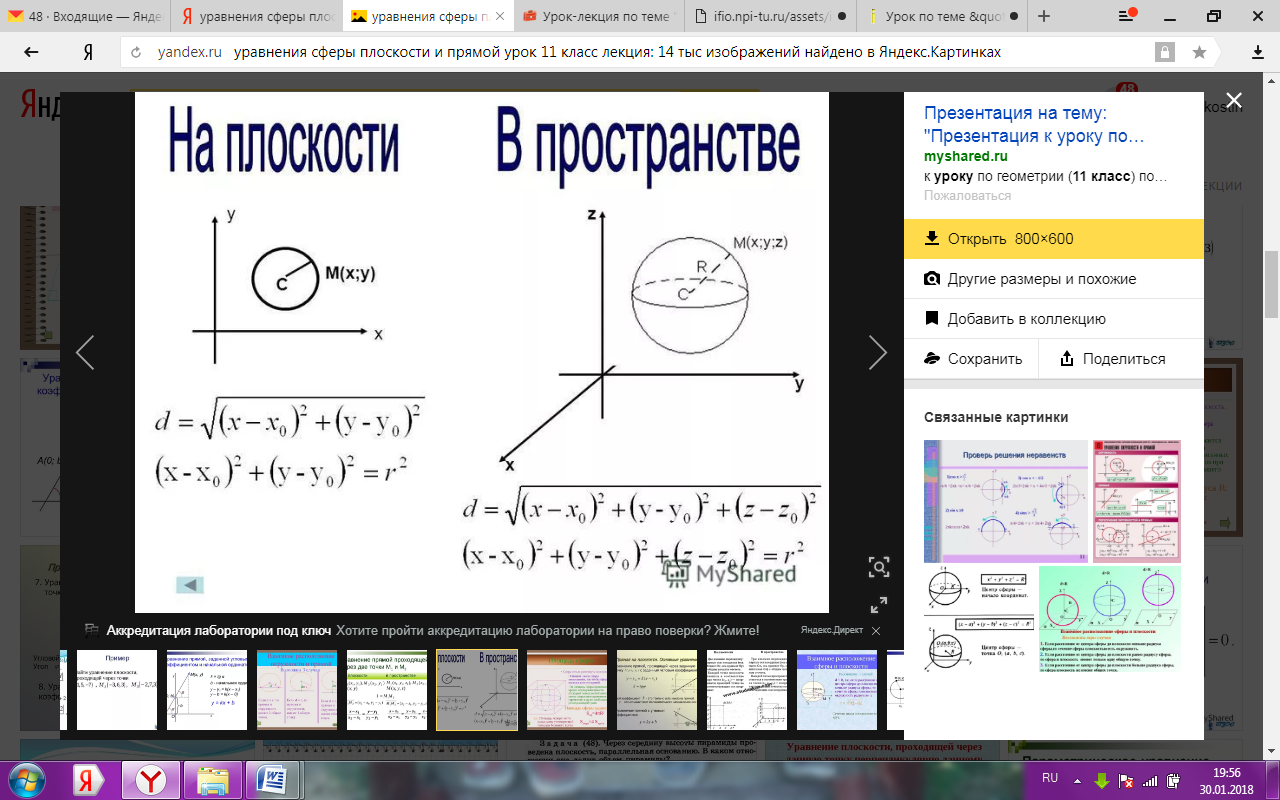
R – радиус сферы, т. О – центр сферы.
Написать уравнение сферы с центром в точке О(1; 2; -5) и радиусом R=3.
Подставим в уравнение сферы: (х-1) 2 +(у-2) 2 +(z-(-5)) 2 =3 2 .
Упростим: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.
Ответ: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.
Пример 2. Дано уравнение сферы: (х-6) 2 +(у+3) 2 +(z-4) 2 =64. Найти координаты центра и радиус сферы.
1)найдем координаты центра: (х-6) 2 +(у-(-3)) 2 +(z-4) 2 =64
2)найдем радиус: R 2 =64, R=√64=8,
Ответ: О(6, -3, 4), R = 8.
Задание 1. Написать уравнение сферы с центром в точке О(5; -2; 3) и радиусом R= 6
Задание 2. Дано уравнение сферы (х-3) 2 +(у+7) 2 +(z-8) 2 =25. Найти координаты центра и радиус сферы.
💥 Видео
Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать
Уравнение плоскости. Практическая часть. 11 класс.Скачать
11 класс, 8 урок, Уравнение плоскостиСкачать
Уравнение плоскости. Практика. Урок 5. Геометрия 11 классСкачать
Частные случаи уравнения плоскости. 1 часть. 11 класс.Скачать
Стереометрия 10 класс. Часть 1 | МатематикаСкачать
1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать
5. Нормальное уравнение плоскости выводСкачать
Семинар №5 Контрольная работа 1Скачать
11. Прямая в пространстве и ее уравненияСкачать
3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать
Уравнение плоскости через 3 точкиСкачать
Видеоурок "Общее уравнение плоскости"Скачать
Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать
Видеоурок "Уравнение плоскости по трем точкам"Скачать
