Данный раздел будет полностью посвящен теме «Уравнение плоскости в отрезках». Мы последовательно рассмотрим, какой вид имеет уравнение плоскости в отрезках, применение этого уравнения для построения заданной плоскости в прямоугольной системе координат, переход от общего уравнения плоскости к уравнению плоскости в отрезках. В статье мы рассмотрим большое количество примеров, которые облегчат усвоение информации.
- Уравнение плоскости в отрезках – описание и примеры
- Приведение общего уравнения плоскости к уравнению плоскости в отрезках
- Уравнение плоскости в отрезках
- Приведение уравнения плоскости в отрезках к общему виду
- Приведение общего уравнения плоскости к уравнению плоскости в отрезках
- 4.2.3. Уравнение плоскости в отрезках
- 📹 Видео
Видео:Видеоурок "Уравнение плоскости в отрезках"Скачать

Уравнение плоскости в отрезках – описание и примеры
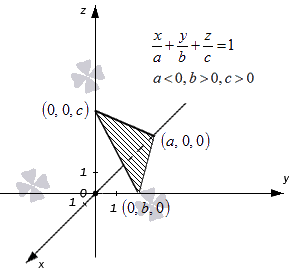
Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 , где a , b и c – это действительные числа, отличные от нуля. Абсолютные величины чисел a , b и c равны длинам отрезков, которые отсекаются плоскостью на осях координат O х , O у и O z в трехмерной системе координат O х у z . Откладываются длины отрезков от начала координат. Направление, в котором необходимо отложить длину отрезка, определяет знак, стоящий перед числом. Наличие «-» свидетельствует о том, что отрезок надо откладывать от нуля в отрицательном направлении оси.
Действительно, координаты точек a , 0 , 0 , 0 , b , 0 , 0 , 0 , c удовлетворяют уравнению плоскости в отрезках:
a a + 0 b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + b b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + 0 b + c c = 1 = 1 ⇔ 1 = 1
Поясним этот момент, расположив заданные точки на графике.
Проиллюстрируем описанное выше примером.
Плоскость проходит через точки — 2 , 0 , 0 , 0 , 3 , 0 и 0 , 0 , — 1 2 на осях координат в прямоугольной системе координат O x y z . Необходимо записать уравнение плоскости в отрезках.
Решение
Определим положение отрезков, отсекаемых плоскостью на осях координат. На оси абсцисс откладываем в отрицательном направлении отрезок длиной 2 единицы. На оси ординат в положительном направлении откладываем отрезок длиной 3 . На оси аппликат в отрицательном направлении откладываем отрезок длиной 1 2 .
При этом, уравнение плоскости в отрезках будет иметь вид: x — 2 + y 3 + z — 1 2 = 1 .
Ответ: x — 2 + y 3 + z — 1 2 = 1
Уравнение плоскости в отрезках удобно использовать для построения чертежей. Проиллюстрируем это утверждение примером.
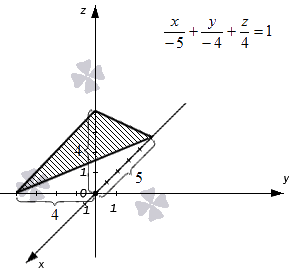
Плоскость в прямоугольной системе координат O х у z задана уравнением плоскости в отрезках вида x — 5 + y — 4 + z 4 = 1 . Необходимо изобразить эту плоскость на графике.
Решение
Изобразим оси координат, обозначаем начало координат и единичные отрезки на осях. Отмечаем длины отрезков, отсекаемых плоскостью, на каждой из осей. Соединяем концевые точки отрезков прямыми линиями. Полученная плоскость имеет вид треугольника. Она соответствует заданному уравнению плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .
Ответ:
Плоскость может быть задана уравнением плоскости другого вида. Для того, чтобы изобразить заданную плоскость на чертеже, можно сначала перейти к уравнению плоскости в отрезках. Получив уравнение плоскости в отрезках, нам останется лишь отметить точки a , 0 , 0 , 0 , b , 0 , 0 , 0 , c и соединить их прямыми линиями.
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Приведение общего уравнения плоскости к уравнению плоскости в отрезках
Мы имеем общее уравнение плоскости в пространстве вида A x + B y + C z + D = 0 . И мы можем получить уравнение плоскости в отрезках. Сделать это можно в том случае, если плоскость пересекает все координатные оси, причем не в начале координат.
Не получится перевести общее уравнение плоскости в пространстве в уравнение плоскости в отрезках в тех случаях, когда плоскость проходит через одну из координатных осей или располагается параллельно оси. Другими словами, мы можем работать лишь с полным уравнением плоскости вида A x + B y + C z + D = 0 , где A ≠ 0 , B ≠ 0 , C ≠ 0 , D ≠ 0 .
Приведение общего уравнения плоскости к уравнению плоскости в пространстве производится следующим образом. Переносим слагаемое D в правую часть уравнения с противоположным знаком.
A x + B y + C z + D = 0 ⇔ A x + B y + C z = — D
Так как D ≠ 0 , то обе части полученного уравнения можно разделить на – D : A — D x + B — D y + C — D z = 1 .
Так как A ≠ 0 , B ≠ 0 , C ≠ 0 , то мы можем отправить в знаменатели коэффициенты перед переменными x , y и z . Последнее уравнение эквивалентно равенству x — D A + y — D B + z — D C = 1 . При этом мы использовали очевидное равенство p q = 1 q p , p , q ∈ R , p ≠ 0 , q ≠ 0 .
В итоге, мы получаем уравнение плоскости в отрезках. Это становится хорошо видно в том случае, если обозначить — D A = a , — D B = b , — D C = c .
Разберем решение примера.
Плоскость в прямоугольной системе координат O x y z в пространстве задана уравнением вида 3 x + 9 y — 6 z — 6 = 0 . Переведем это уравнение в уравнение плоскости в отрезках.
Решение
Данное в условии задачи уравнение является полным уравнением плоскости. Это дает нам возможность привески его к уравнению плоскости в отрезках. Перенесем — 6 в правую часть равенства, а затем разделим обе части равенства на 6 :
3 x + 9 y — 6 z — 6 = 0 ⇔ 3 x + 9 y + 6 z = 6 3 x + 9 y — 6 z = 6 ⇔ 1 2 x + 3 2 y — z = 1
Коэффициенты при переменных x, y и z отправим в знаменатели: 1 2 x + 3 2 y — z = 1 ⇔ x 2 + y 2 3 + z — 1 = 1 . Полученное уравнение и есть уравнение плоскости в отрезках.
Ответ: x 2 + y 2 3 + z — 1 = 1
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение плоскости в отрезках
В данной статье мы рассмотрим уравнение плоскости в отрезках. Представим методы преобразования уравнения плоскости в отрезках в уравнение плоскости в общем виде и обратно. Рассмотрим численные примеры.
Уравнение плоскости в отрезках представляется следующей формулой:
 , , | (1) |
где a, b, c отличные от нуля числа.
Отметим, что числа a, b, c в уравнении (1) имеют простой геометрический смысл. Они равны длинам отрезков, которые отсекает плоскость на осях Ox, Oy, Oz (Рис.1, Рис.2).
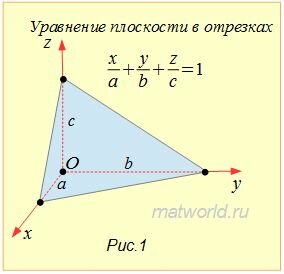 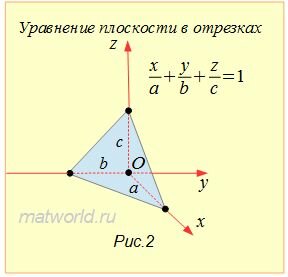 |
Действительно. Подставляя в (1) y=0, z=0 получим x=a, если же подставить в (1) x=0, y=0 то получим z=c, подставвляя, наконец, x=0, z=0 получим y=b. Таким образом плоскость, определяемая уравнением (1) проходит через точки M1(a, 0, 0), M2(0, b, 0) и M3(0, 0, с).
Пример 1. Составить уравнение прямой, которая пересекает оси Ox, Oy и Oz в точках −1,3 и 7, соответственно.
Решение. Подставляя значения a=−1, b=3 и c=7 в (1), получим:
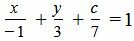 . . |
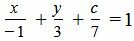 . . |
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Приведение уравнения плоскости в отрезках к общему виду
Левая часть уравнения (1) приведем к общему знаменателю:
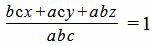 . . |
Далее, умножив обе части уравнения на abc, получим:
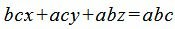 |
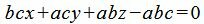 . . |
Пример 2. Уравнение плоскости в отрезках представлено следующим уравнением:
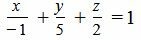 . . |
Перевести уравнение к общему виду.
Решение. Приведем левую часть уравнения к общему знаменателю:
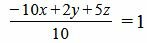 . . |
Умножив обе части уравнения на 10, получим:
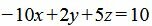 |
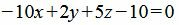 . . |
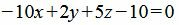 . . |
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Приведение общего уравнения плоскости к уравнению плоскости в отрезках
где A, B, C, D − отличные от нуля числа, т.е. уравнение плокости является полным (о полных и неполных уравнениях плоскости смотрите здесь).
Сделаем следующие преобразования. Переведем свободный член D на правую часть уравнения и разделим обе части уравнения на −D:
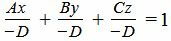 . . | (2) |
Уравнение (2) можно переписать в следующем виде:
 . . | (3) |
Сделаем следующие обозначения:
 |
Тогда получим уравнение прямой в отрезках (1).
Пример 3. Привести общее уравнение прямой
к уравнению прямой в отрезках.
Решение. Так как все коэффициенты уравнения отличны от нуля, можно построить уравнение плоскости в отрезках. Воспользуемся формулой (3). Имеем: A=−2, B=3, C=5, D=−4. Подставив эти значения в формулу (3), получим:
Видео:Уравнение плоскости. 11 класс.Скачать

4.2.3. Уравнение плоскости в отрезках
Предположим, что все коэффициенты в уравнении плоскости (3) отличны от нуля. Тогда, перенеся D в правую часть равенства и разделив обе части равенства на –D, получим уравнение
Где Р = —D/А, Q = —D/B, a R = —D/C.. Уравнение (4) называется уравнением плоскости В отрезках. Числа Р, Q и R имеют простой геометрический смысл – это величины отрезков, которые плоскость отсекает на координатных осях. Чтобы убедиться в этом, достаточно заметить, что точки с координатами <P,0,0>, <0,Q,0> и <0,0,R> удовлетворяют уравнению (4).
📹 Видео
1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Видеоурок "Общее уравнение плоскости"Скачать

11. Прямая в пространстве и ее уравненияСкачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

5. Нормальное уравнение плоскости выводСкачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Видеоурок "Уравнение прямой в отрезках"Скачать

Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Математика без Ху!ни. Уравнение касательной.Скачать

Угловой коэффициент в уравнении прямой. Геометрический смысл углового коэффициента. Геометрия 8 клСкачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать