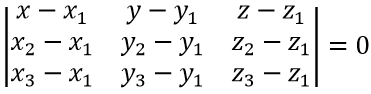Уравнение плоскости в кубе через 3 точки (2 видео)

Уравнение плоскости, которая проходит через три заданные точки, не лежащие на одной прямой.

В этой статье мы разберемся с задачей нахождения уравнения плоскости в прямоугольной системе координат в трехмерном пространстве, когда известны координаты трех различных точек этой плоскости, не лежащих на одной прямой. Сначала покажем принцип нахождения уравнения плоскости, после чего перейдем к решению примеров и задач, в которых требуется составить уравнение плоскости, проходящей через три заданные точки.

Навигация по странице.

Содержание

Нахождение уравнения плоскости, проходящей через три заданные точки.
Примеры составления уравнения плоскости, проходящей через три заданные точки.
Уравнение плоскости, проходящей через три точки
Уравнение плоскости через 3 точки
Уравнение плоскости, проходящей через 3 точки, через смешанное произведение векторов
Готовые работы на аналогичную тему
Уравнение плоскости, заданной 3 точками, через нормальный вектор и точку
🎬 Видео

Видео:Уравнение плоскости через 3 точкиСкачать

Нахождение уравнения плоскости, проходящей через три заданные точки.

Прежде чем приступать к составлению уравнения плоскости, проходящей через три заданные точки пространства, вспомним одну аксиому: через три несовпадающие и не лежащие на одной прямой точки трехмерного пространства проходит единственная плоскость. Таким образом, задав три различных и не лежащих на одной прямой точки, мы в трехмерном пространстве однозначно определим плоскость, проходящую через эти точки.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , в ней заданы три несовпадающие точки , которые не лежат на одной прямой. Поставим перед собой следующую задачу: написать уравнение плоскости, проходящей через эти три точки.

Покажем два способа ее решения.

Первый способ составления уравнения плоскости, проходящей через три заданные точки .

Известно, что общее уравнение плоскости вида задает в прямоугольной системе координат Oxyz плоскость , которая проходит через точку , а нормальный вектор плоскости имеет координаты . Следовательно, мы можем составить общее уравнение плоскости, если знаем координаты точки, через которую она проходит, и координаты нормального вектора этой плоскости. От этого знания и будем отталкиваться при нахождении уравнения плоскости, проходящей через три заданные точки .

Итак, из условия задачи нам известны координаты точки (даже координаты трех точек), через которую проходит плоскость, уравнение которой нам требуется составить. Осталось отыскать координаты нормального вектора этой плоскости.

Так как нормальный вектор плоскости и любой ненулевой вектор этой плоскости перпендикулярны, то вектор перпендикулярен как вектору , так и вектору . Следовательно, в качестве вектора можно принять векторное произведение векторов и . Так как и (при необходимости обращайтесь к статье вычисление координат вектора по координатам точек), то . После вычисления записанного определителя, станут видны координаты нормального вектора , и можно записывать требуемое уравнение плоскости, проходящей через три заданные точки.

Второй способ нахождения уравнения плоскости, проходящей через три заданные точки .

Очевидно, что множество точек определяет в прямоугольной системе координат Oxyz в трехмерном пространстве плоскость, проходящую через три различные и не лежащие на одной прямой точки , тогда и только тогда, когда три вектора и компланарны.

Следовательно, должно выполняться условие компланарности трех векторов и , то есть, смешанное произведение векторов должно быть равно нулю: . Это равенство в координатной форме имеет вид . Оно, после вычисления определителя, представляет собой общее уравнение плоскости, проходящей через три заданные точки .

Далее, от полученного общего уравнения плоскости, проходящей через три заданные точки, Вы при необходимости можете перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости.

Осталось рассмотреть решения примеров, в которых находится уравнение плоскости, проходящей через три несовпадающие и не лежащие на одной прямой точки.

Видео:Видеоурок "Уравнение плоскости по трем точкам"Скачать

Примеры составления уравнения плоскости, проходящей через три заданные точки.

В предыдущем пункте статьи мы рассмотрели два способа нахождения уравнения плоскости, проходящей через три различные и не лежащие на одной прямой точки. Давайте рассмотрим их применение при решении задачи.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение плоскости, проходящей через три точки

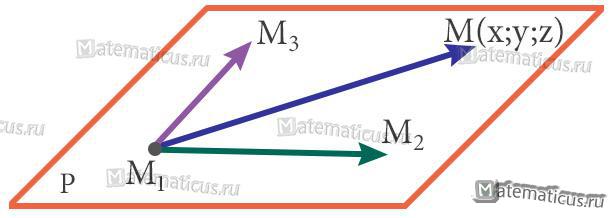
Если плоскость проходит через три точки М₁(x₁;y₁;z₁), M₂(x₂;y₂;z₂) и M₃₍x₃;y₃;z₃), не лежащие на одной прямой, то проходящая через них плоскость представляется уравнением:

Точка М(х; у; z) лежит в одной плоскости с точками M₁, M₂ и M₃ только в том случае, когда векторы:

Точки M₁(2;3;1), M₂(1;2;2) и M₃(1;5;4) не лежат на одной прямой, так как

Плоскость с точками M₁, M₂ и M₃ представляется уравнением

Видео:Сечение через три точки, лежащие в разных плоскостяхСкачать

Уравнение плоскости через 3 точки

Вы будете перенаправлены на Автор24

Для начала стоит напомнить, как выглядит общее уравнение плоскости:

$Ax cdot + By + Cz + D = 0left(1right)$,

при этом: $$ — координаты нормального вектора данной плоскости, а $D$ — свободный член.

В общем уравнении коэффициенты $A, B, C$ не могут быть одновременно равны нулю, если же один из коэффициентов нулевой — уравнение называется неполным. При $D=0$ плоскость проходит через центр осей координат.

Также в дальнейшем нам пригодится уравнение плоскости, заданной точкой, лежащей в данной плоскости и нормальным вектором:

здесь $(x_0; y_0; z_0)$ — координаты точки плоскости.

Теперь непосредственно к делу.

Уравнение плоскости через три точки можно выразить несколькими способами: с помощью смешанного произведения векторов и выразив сначала нормальный вектор плоскости и используя одну точку.

Видео:Как строить сечение куба? Стереометрия. 10-11 класс | Математика | TutorOnline Скачать

Уравнение плоскости, проходящей через 3 точки, через смешанное произведение векторов

Рассмотрим три точки $M_1, M_2, M_3$, не находящиеся на одной прямой. Соответственно аксиоме стереометрии о том, что три точки задают плоскость, и притом только одну, все эти точки лежат в одной плоскости $α$.

Рисунок 1. Плоскость через 3 точки. Автор24 — интернет-биржа студенческих работ

Рассмотрим точку $M$, лежащую в плоскости $α$. Если описать плоскость $α$ как множество точек $M$, вектора $vec$, $vec$ и $vec$ должны быть компланарны между собой. А как известно, вектора компланарны между собой если их смешанное произведение равно нулю.

Соответственно, для того чтобы вычислить это смешанное произведение, необходимо вычислить определитель третьего порядка, каждая строка которого является координатами вышеперечисленных векторов.

Готовые работы на аналогичную тему

Пусть координаты точек $M, M_1, M_2, M_3$ — $(x; y; z), (x_1;y_1; z_1), (x_2;y_2; z_2), (x_3;y_3;z_3)$ соответственно. Тогда координаты каждого из вышеперечисленных векторов составят:

Составим определитель, описывающий смешанное произведение векторов:

$begin x-x_1 && y-y_1 && z-z_1 \ x_2-x_1 && y_2-y_1 && z_2-z_1 \ x_3-x_1 && y_3-y_1 &&z_3-z_1 \ end=0$ — уравнение плоскости через 3 точки.

При вычислении этого определителя получается общее уравнение плоскости, проходящей через три точки. Это можно увидеть, раскрыв определитель по первой строке:

$begin y_2-y_1 && z_2-z_1 \ y_3-y_1 &&z_3-z_1 \ end cdot ( x-x_1) + begin x_2-x_1 && z_2-z_1 \ x_3-x_1 &&z_3-z_1 \ end cdot (y-y_1) + begin x_2-x_1 && y_2-y_1 \ x_3-x_1 && y_3-y_1 \ end cdot (z-z_1) = 0left(3right)$.

Коэффициенты из уравнения $(3)$ также совпадают с координатами векторного произведения $vec×vec$ и, так как два этих вектора неколлинеарны и параллельны рассматриваемой плоскости $α$, данное векторное произведение представляет собой нормальный вектор к плоскости, для которой составляется уравнение.

Видео:Построение сечения куба по трем точкамСкачать

Уравнение плоскости, заданной 3 точками, через нормальный вектор и точку

Другим альтернативным методом задания плоскости является использование нормального вектора плоскости и точки, принадлежащей данной плоскости.

Для того чтобы воспользоваться данным методом, найдём векторное произведение векторов $vec$ и $vec$:

$[vec × vec]= begin vec &&vec &&vec \ x_2-x_1 &&y_2-y_1 &&z_2-z_1 \ x_3-x_1 &&y_3-y_1 &&z_3-z_1 \ end=0$.

Данное произведение является нормальным вектором плоскости, для которой составляется уравнение. Полученные координаты нормального вектора можно использовать непосредственно для составления уравнения плоскости.

Зная точку, принадлежащую этой плоскости, можно подставить координаты нормального вектора и координаты точки в уравнение $(2)$ и получить уравнение плоскости:

В этом уравнении $n_x; n_y; n_z$ — координаты нормального вектора, определённого из векторного произведения векторов $vec$ и $vec$, а $(x_3; y_3; z_3)$ — некая точка, принадлежащая данной плоскости.

По сути, два вышеприведённых метода представляют одно и то же, так как в обоих необходимо найти координаты нормального вектора и затем, используя их и координаты третьей неиспользованной точки, получить уравнение самой плоскости.

К данной задаче можно также свести задачу с нахождением уравнения плоскости по уравнениям лежащих в ней параллельных и пересекающихся прямых.

Cоставить уравнение плоскости, проходящей через 3 точки $M_1,M_2, M_3$ c координатами $(1;2;3), (1;2;4)$ и $(4;2;-1)$ соответственно.

Воспользуемся вторым способом и найдём координаты вектора через векторное произведение. Для этого сначала выразим координаты векторов:

Найдём их векторное произведение:

Подставим координаты нормального вектора в уравнение $(2)$:

$0cdot(x-4)+(-3) cdot (y-2)+0 cdot(z+1)=0$.

$-3y+6=0$ — искомое уравнение плоскости.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 14 03 2021