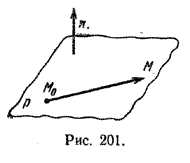
Пусть дана некоторая точка M0 и ненулевой вектор n. Через точку M0 можно провести только одну плоскость р перпендикулярную вектору n (рис. 201).
Выведем уравнение плоскости р. Пусть М — произвольная точка пространства. Очевидно, что точка М принадлежит плоскости р тогда и только тогда, когда вектор (overrightarrow<M_M>) перпендикулярен вектору n. Как известно, необходимым и достаточным условием перпендикулярности двух векторов является равенство нулю их скалярного произведения. Поэтому уравнение плоскости, проходящей через точку M0 перпендикулярно вектору n, может быть записано в виде
Вектор n в уравнении (1) называется нормальным вектором плоскости. В качестве нормального вектора можно взять любой вектор, перпендикулярный плоскости.
Пусть точка M0 и вектор n заданы своими координатами в некоторой прямоугольной системе координат:
Обозначим координаты произвольной точки М плоскости р через х, у и z. Тогда вектор (overrightarrow<M_M>) имеет координаты х — х0, у — у0 и z — z0, а уравнение (1) в координатах записывается следующим образом:
Это уравнение называется уравнением плоскости, проходящей через точку (х0; у0; z0) перпендикулярно вектору (А; В; С).
Задача 1. Найти уравнение плоскости, проходящей через точку М0(-3; 4; 7) перпендикулярно вектору n = (1; —2; 6).
В данном случае х0 = -3, у0 = 4, z0 = 7; А = 1, В = -2, С = 6. Подставив эти значения в уравнение (2), получим искомое уравнение
3адачa 2. Даны точки M1 (2; -1; 3) и M2(4; 5; 0). Написать уравнение плоскости, проходящей через точку М2 перпендикулярно вектору (overrightarrow<M_M_2>).
За нормальный вектор плоскости можно взять вектор n = (overrightarrow<M_M_2>) = (2; 6; -3). После подстановки координат нормального вектора и координат точки М0 = М2(4; 5; 0) в уравнение (2) получим
Задача 3. В треугольнике с вершинами в точках А1<-5; 2; 7), А2(5; 0; 6), А3(0; -1; 2) проведена медиана А1М0. Найти уравнение плоскости, проходящей через точку М0 перпендикулярно медиане А1М0.
За нормальный вектор плоскости можно принять вектор n = (overrightarrow<A_M_0>). Определим его координаты. Точка М0 — середина отрезка А2А3, поэтому, если (х0; у0; z0) — ее координаты, то
Координаты нормального вектора n = (А; В; С), следовательно, равны
A = 5 /2 + 5 = 15 /2, В = — 1 /2 — 2 = — 5 /2, С = 4 — 7 = — 3.
- Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн
- Предупреждение
- Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения
- Уравнение плоскости через координаты вектора нормали и точки: онлайн-калькулятор
- Как найти уравнение плоскости через координаты вектора нормали и точки с помощью онлайн-калькулятора
- Материалы, которые помогут вам лучше разобраться в теме:
- Уравнение плоскости через точку перпендикулярно вектору онлайн
- 📺 Видео
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через данную точку и перпендикуляной данной прямой. Дается подробное решение с пояснениями. Для построения уравнения плоскости задайте вид уравнения прямой (канонический или параметрический) введите координаты точки и коэффициенты уравнения прямой в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Уравнение плоскости, проходящей через данную точку и перпендикулярной данной прямой − теория, примеры и решения
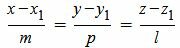 . . | (1) |
Построить уравнение плоскости α, проходящей через точку M0 и перпендинулярной прямой L.
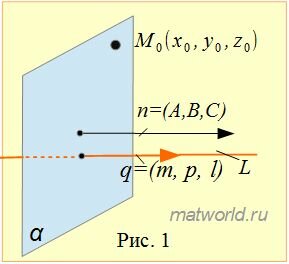 |
Решение. Уравнение плоскости, проходящей через точку M0 и имеющий нормальный вектор n=<A, B, C> имеет следующий вид:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (2) |
Направляющий вектор прямой L имеет вид q=<m, p, l>. Поскольку прямая L и плоскость α перпендикулярны друг другу, следовательно нормальный вектор плоскостти и направляющий вектор прямой должны быть коллинеарны (Рис.1). Тогда вместо координат нормального вектора плоскости нужно подставить координаты направляющего вектора прямой L. Получим следующее уравнение плоскости:
| m(x−x0)+p(y−y0)+l(z−z0)=0. | (3) |
Упростим уравнение (3):
| mx+py+lz+D=0, | (4) |
Таким образом уравнение (4) определяет плоскость, проходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1).
Ответ. Уравнение плоскости прпоходящей через точку M0(x0, y0, z0) и перпендикулярной прямой (1) имеет вид (4).
Пример 1. Найти уравнение плоскости α, проходящую через точку M0(3, −1, 2) и перпендикулярной прямой L:
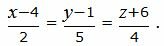 | (7) |
Решение. Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой (2).
Направляющий вектор прямой L имеет следующий вид: :
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (2) примет следующий вид:
| m(x−x0)+p(y−y0)+l(z−z0)=0. | (8) |
Подставляя координаты точки M0 и направляющего вектора q в (8), получим:
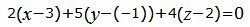 | (9) |
Упростим уравнение (9):
| 2x+5y+4z−9=0. | (10) |
Ответ: Уравнение плоскости, проходящей через точку M0(3, −1, 2) и перпендикулярной прямой (7) имеет вид (10).
Пример 2. Найти уравнение плоскости α, проходящую через точку M0(4, 3, −6) и перпендикулярной прямой L, заданной параметрическим уравнением:
 | (11) |
Решение. Приведем параметрическое уравнение (11) к каноническому виду:
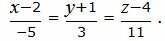 | (11′) |
Уравнение плоскости α, проходящей через точку M0(x0, y0, z0) и имеющий нормальный вектор n=<A, B, C> представляется формулой:
| A(x−x0)+B(y−y0)+C(z−z0)=0. | (12) |
Направляющий вектор прямой L имеет следующий вид:
Для того, чтобы прямая L была перпендикулярна плоскости α, нормальный вектор плоскости α должен быть коллинеарным направляющему вектору прямой L, т.е. уравнение плоскости (12) примет следующий вид:
| m(x−x0)+p(y−y0)+l(z−z0)=0. | (13) |
Подставляя координаты точки M0 и направляющего вектора q в (13), получим:
 |
Упростим уравнение (13):
| −5x+3y+11z+77=0. | (14) |
Ответ. Уравнение плоскости, проходящей через точку M0(4, 3, −6) и перпендикулярной прямой (11) имеет вид (14).
Видео:Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

Уравнение плоскости через координаты вектора нормали и точки: онлайн-калькулятор
Плоскость — это бесконечная поверхность с принадлежащими ей прямыми, через которые проходят любые две ее точки. Нормалью к кривой в указанной точке является прямая, расположенная перпендикулярно к касательной прямой в заданной точке кривой.
Если указаны координаты точки A ( x 1 , y 1 , z 1 ) , принадлежащей плоскости, и вектор нормали n = , то уравнение плоскости соответствует формуле:
A ( x — x 1 ) + B ( y — y 1 ) + C ( z — z 1 ) = 0 .
Чтобы найти уравнение плоскости, перпендикулярной вектору онлайн, необходимо:
- указать значение точки A ;
- заполнить значение вектора;
- воспользоваться кнопкой «Рассчитать».
Видео:2. Уравнение плоскости примеры решения задач #1Скачать

Как найти уравнение плоскости через координаты вектора нормали и точки с помощью онлайн-калькулятора
Рассмотрим пример, наглядно демонстрирующий работу с онлайн-калькулятором. Пусть нужно найти уравнение плоскости по вектору нормали к ней и координатам точки, лежащей в плоскости. Для этого в онлайн-калькуляторе просто зададим известную точку и соответствующий вектор (нормаль):
Впишем значения в пустые поля и нажмем «Рассчитать» (значения взяты произвольно):
После этого калькулятор автоматически выдаст подробное решение с ответом:
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Материалы, которые помогут вам лучше разобраться в теме:
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Уравнение плоскости через точку перпендикулярно вектору онлайн
Сервис предназначен для геометрических вычислений, которыми пользуются учащиеся школ и студенты университетов для подготовки к занятиям.
Решение задачи с помощью онлайн-калькулятора имеет преимущества:
- формула в основе автоматических подсчетов дает точный ответ без ошибок и опечаток;
- нет необходимости искать нужный способ расчета;
- пользователю доступно подробное решение;
- производить расчеты можно неограниченное количество раз бесплатно.
Пошаговые вычисления позволяют учащемуся вникнуть в процесс решения задачи по геометрии и справляться с заданиями самостоятельно. Подготовка к занятиям благодаря калькулятору занимает меньше времени и происходит более продуктивно.
📺 Видео
4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Уравнение плоскости через 2 точки параллельно векторуСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Уравнение плоскости, проходящей через заданную точку перпендикулярно заданному направлению.Скачать

Уравнение плоскости через точку и нормальСкачать

Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать

3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Составьте уравнение плоскости, проходящей через ось Оу и точку M (3;2;4).Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Метод координат Урок №2 2 Нахождение уравнения плоскости по трем точкамСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

5. Нормальное уравнение плоскости выводСкачать

Уравнение плоскости через 2 точки параллельно прямойСкачать