Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.
- Найти уравнение плоскости
- Ввод данных в калькулятор для составления уравнения плоскости
- Дополнительные возможности калькулятора для вычисления уравнения плоскости
- Теория. Уравнение плоскости.
- Уравнение плоскости по трём точкам
- Уравнение плоскости по трем точкам
- Первая точка
- Вторая точка
- Третья точка
- Плоскость, проходящая через три точки
- Уравнение плоскости онлайн
- Предупреждение
- Уравнение плоскости, проходящей через три точки
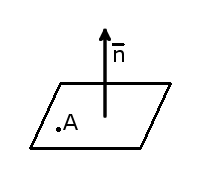
- Уравнение плоскости, проходящей через одну точку и имеющий нормаль n
- 📽️ Видео
Видео:Видеоурок "Уравнение плоскости по трем точкам"Скачать
Найти уравнение плоскости
Выберите метод решения исходя из имеющихся в задаче данных:
В задаче известны:
Ввод данных в калькулятор для составления уравнения плоскости
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления уравнения плоскости
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Уравнение плоскости.
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки
В зависимости от условий задачи уравнение плоскости можно составить следующими способами:
- Если заданы координаты трех точек A( x 1, y 1, z 1), B( x 2, y 2, z 2) и C( x 3, y 3, z 3), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле
| x — x 1 | y — y 1 | z — z 1 | = 0 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 | |
| x 3 — x 1 | y 3 — y 1 | z 3 — z 1 |
Если заданы координаты точки A( x 1, y 1, z 1) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Видео:Уравнение плоскости через 3 точкиСкачать
Уравнение плоскости по трём точкам
Этот онлайн-калькулятор выводит общее уравнение плоскости по трем точкам
В математике, плоскость — это плоская, двумерная поверхность, которая простирается бесконечно далеко
Общее уравнение плоскости выглядит так:
Плоскость может быть проведена через три не коллинеарные точки ( точки не лежат на одной прямой). И калькулятор ниже может это сделать. Вы вводите координаты трех точек, и калькулятор вычисляет уравнение плоскости, проходящей через эти три точки. Как всегда, объяснения и теорию вы можете найти ниже под калькулятором.
Уравнение плоскости по трем точкам
Первая точка
Вторая точка
Третья точка
Плоскость, проходящая через три точки
Зная три точки плоскости, мы знаем, что они удовлетворяют уравнению плоскости. Мы можем выразить это математически:
Точки нам даны, и коэффициенты a, b, c, d нужно найти. Это значит, что мы составляем систему из трех линейных уравнений с четырьмя переменными a, b, c, d:
Или в матричной форме это будет выглядеть так:
Хоть мы и имеем только три уравнения для трех неизвестных, это означает, что система уравнений имеет бесконечное множество решений; тем не менее мы все еще можем использовать этот калькулятор — Решение системы линейных алгебраических уравнений методом Гаусса для получения решения в стандартной форме с неизвестными переменнами ( это значит, что переменные могу принимать любое значение).
В нашем случае, мы имеет только одну независимую переменную. Если все координаты — целые числа, то калькулятор выбирает значение неизвестной переменной так, чтобы оно было наименьшим общим кратным (НОК) из всех знаменателей с другими коэффициентами, чтобы избавиться от фракций в ответе. Если координаты — не целые числа, значение независимой переменной нужно принять за 1.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать
Уравнение плоскости онлайн
С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через три точки, и уравнение плоскости, проходящей через одну точку и имеющий заданный нормаль плоскости. Дается подробное решение с пояснениями. Для построения уравнения плоскости выберите вариант задания исходных данных, введите координаты точек в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Репетитор по математике пишет уравнение плоскости по трем точкамСкачать
Уравнение плоскости, проходящей через три точки
Рассмотрим цель − вывести уравнение плоскости, проходящей через три различные точки M1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3), не лежащие на одной прямой. Так как эти точки не лежат на одной прямой, векторы 
и 
не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M1, M2, M3 тогда и тольно тогда, когда векторы M1M2, M1M3 и 
компланарны. Но векторы M1M2, M1M3, M1M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов M1M2, M1M3, M1M в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к указанной плоскости:
 |
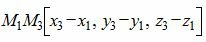
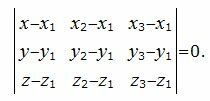Разложив определитель в левой части выражения, например, по первому столбцу и упростив, получим уравнение плоскости в общей форме, проходящий по точкам M1, M2, M3:
Пример 1. Построить уравнение плоскости, проходящую через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2).
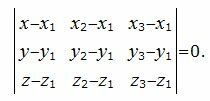| (1) |
Подставляя координаты точек A, B, C в (1), получим:
 |
 |
Разложим определитель по первому столбцу:
   |
  |
 |
Уравнение плоскости, проходящей через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2) имеет вид:
|
Видео:Уравнение плоскости. 11 класс.Скачать
Уравнение плоскости, проходящей через одну точку и имеющий нормаль n
Пример 2. Построить плоскость, проходящую через точку M0(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).
 | (2) |
Подставляя координаты векторов M0 и n в (2), получим:
📽️ Видео
Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать
Уравнение плоскости. Практика. Урок 5. Геометрия 11 классСкачать
Метод координат Урок №2 2 Нахождение уравнения плоскости по трем точкамСкачать
Уравнение плоскости. Практическая часть. 11 класс.Скачать
11 класс, 8 урок, Уравнение плоскостиСкачать
1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать
§41 Уравнение плоскости, проходящей через три данные плоскостиСкачать
3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать
Видеоурок "Уравнение плоскости в отрезках"Скачать
Векторный метод в стереометрии. Задача 14 профильный ЕГЭСкачать
5. Нормальное уравнение плоскости выводСкачать
Лекция 25. Виды уравнений плоскости в пространстве.Скачать
Составьте уравнение плоскости, проходящей через ось Оу и точку M (3;2;4).Скачать
Частные случаи уравнения плоскости. 1 часть. 11 класс.Скачать
