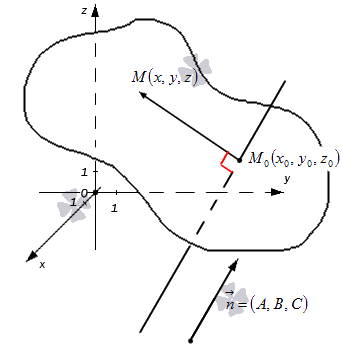
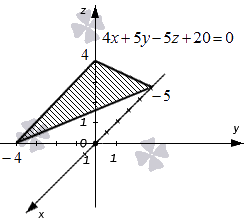
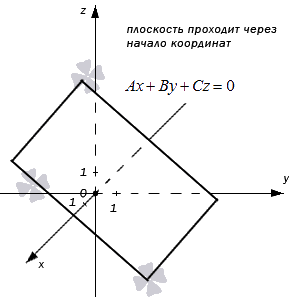
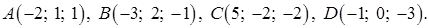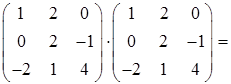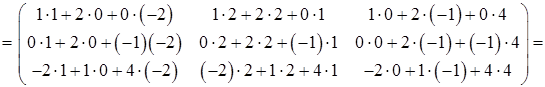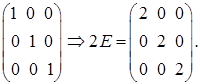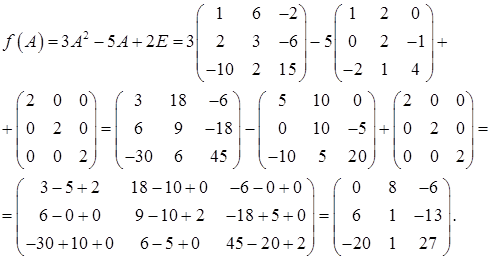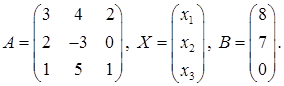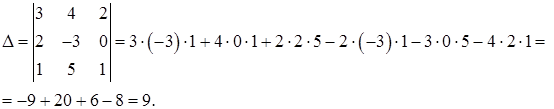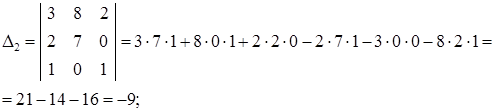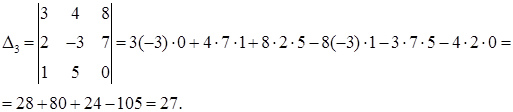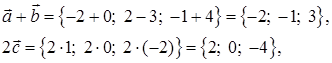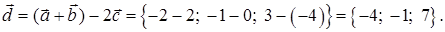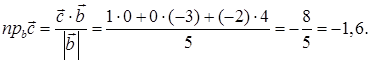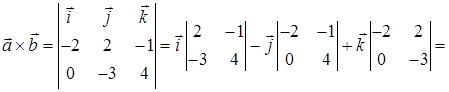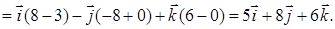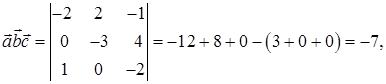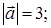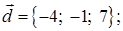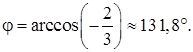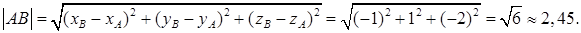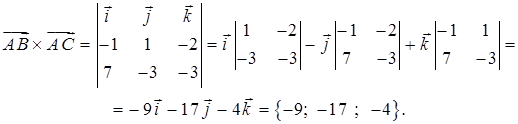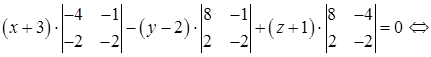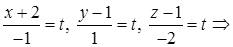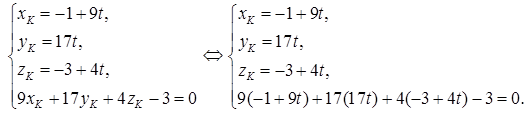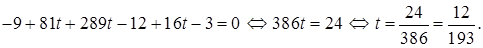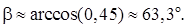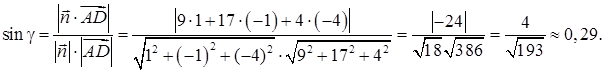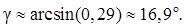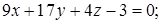Общее уравнение плоскости: 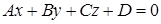
где A, B, C – координаты вектора нормали вектора 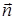
Уравнение плоскости, проходящей через точку 


Уравнение плоскости, проходящей через три заданные точки
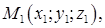

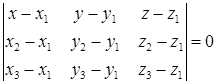
Угол 
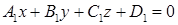


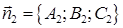
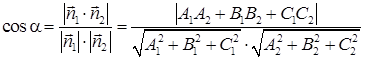
Уравнения прямой в пространстве
Параметрические уравнения прямой l в пространстве:
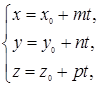
где 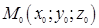
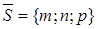
Каждому значению параметра 
Канонические уравнения прямой:

Уравнения прямой, проходящей через две данные точки 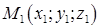
и 

Углом 
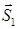


Углом между плоскостью и прямой l (в случае их пересечения) называется угол между прямой и её проекцией на плоскость. Синус угла 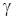
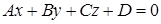

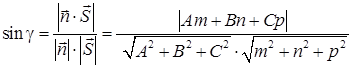
Примерный вариант и образец выполнения
контрольной работы № 2
Задача 1. Даны многочлен f(x) и матрица А:
Требуется найти значение матричного многочлена f (A).
Задача 2. Дана система трех линейных алгебраических уравнений
с тремя неизвестными:
1) записать систему в матричном виде;
2) найти решение системы с помощью формул Крамера;
3) решить систему при помощи обратной матрицы.
Задача 3. Даны координаты трех векторов: 



1) вычислить модуль вектора 
2) найти координаты вектора 
3) найти угол φ между векторами 
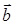
4) вычислить проекцию вектора 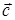
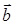
5) вычислить площадь треугольника, построенного на векторах 
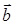
6) вычислить объем параллелепипеда, построенного на векторах 
Задача 4. Даны координаты точек – вершин пирамиды ABCD:
1) вычислить длину ребра AB;
2) найти уравнение плоскости грани ABC;
3) найти угол 
4) составить параметрические уравнения прямой AB;
5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;
6) найти координаты точки пересечения DK и грани ABC;
7) найти угол 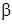
8) найти угол 
9) сделать чертеж пирамиды в системе координат.
Решение задачи 1
Записываем матричный многочлен: 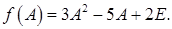
Найдем матрицу A 2 . При умножении матрицы A на себя используем правило «строка на столбец» (формула (23)):
A 2 = A·A =
Найдем матрицу 2Е, используя правило умножения матрицы на число (формула (21)):
E =
Теперь найдем значение матричного многочлена f(A),используя правило умножения матрицы на число и правило сложения матриц (формула (22)):
Ответ:
Решение задачи 2
1) Запишем систему в матричном виде:
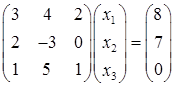
где
(Во втором уравнении системы отсутствует неизвестная х3, т. е. а23 = 0).
2) Решим систему с помощью формул Крамера. Для этого по формулам (29) составляем главный определитель системы из коэффициентов при неизвестных в левых частях уравнений и три вспомогательных определителя:
Вычислим эти определители, используя формулу (25):
Так как ∆ ≠ 0, то данная система имеет единственное решение.
Найдем решение системы по формулам Крамера (30):
3) Решим систему при помощи обратной матрицы.
a) Определитель 
б) Чтобы найти союзную матрицу 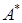
Здесь определители 2-го порядка вычислены по формуле (24).
Тогда союзная матрица (см. формулу (31)):
в) Найдем обратную матрицу по формуле (32):
г) Получим решение системы при помощи обратной матрицы по формуле (33) (правило «строка на столбец»):
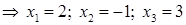
Решение, полученное матричным способом, совпадает с тем, которое получено по формулам Крамера, что подтверждает правильность этого решения.
1) система в матричном виде: AX = B, где
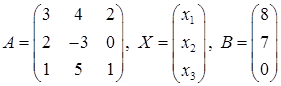
2) решение системы, полученное с помощью формул Крамера:

3) решение системы, полученное при помощи обратной матрицы:

Решение задачи 3
1) Модуль вектора 
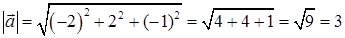
2) Чтобы найти координаты вектора 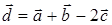
тогда
3) Косинус угла между векторами 
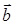
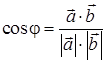
Для этого вычислим скалярное произведение 
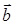

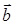
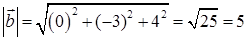

и
4) Проекцию вектора 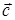
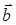
5) Площадь треугольника, построенного на векторах 
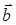
Следовательно, площадь треугольника, построенного на векторах 
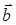
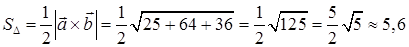
6) Для вычисления объема параллелепипеда, построенного на векторах 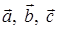
тогда объема параллелепипеда по формуле (47): 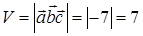
1) модуль вектора 
2) координаты вектора 
3) угол между векторами 
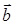
4) проекция вектора 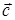
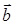
5) площадь треугольника, построенного на векторах 
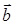
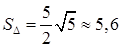
6) объем параллелепипеда, построенного на векторах 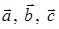
Решение задачи 4
1) Длину ребра 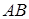
2) Чтобы получить уравнение плоскости грани ABC, необходимо найти вектор, перпендикулярный плоскости ABC, т. е. вектор, перпендикулярный векторам 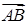
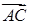
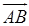
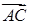
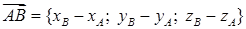
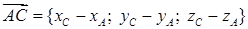
Векторное произведение 
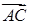
В качестве вектора нормали к плоскости ABC можно взять любой вектор, коллинеарный полученному, например, 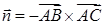
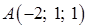
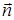



3) Прежде, чем найти угол 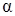
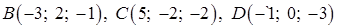
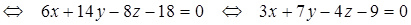
Из уравнения плоскости BCD возьмем координаты вектора нормали 

Косинус угла 
по формуле(50):
Отсюда 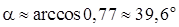
4) Уравнения ребра AB можно записать как параметрические уравнения прямой, проходящей через точку A(–2; 1; 1) и имеющей направляющий вектор 
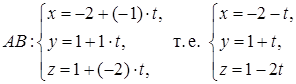
Другой способ: можно использовать уравнения прямой, проходящей через две точки 
откуда, обозначив каждую из дробей t, получаем:

5) Высота пирамиды DK – это прямая, проведенная из вершины D перпендикулярно грани ABC. Она имеет направляющий вектор 
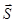
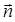
и вектор 

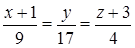
6) Прежде, чем найти точку пересечения DK и грани ABC, получим параметрические уравнения прямой DK. Обозначив каждую из дробей
в канонических уравнениях буквой t, получаем:
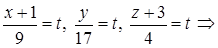

Точка пересечения DK и грани ABC (точка К) лежит на прямой, а значит, имеет координаты 
Решим последнее уравнение относительно t:
Вычислим координаты точки K, подставив найденное значение параметра в первые три уравнения системы:
Итак, точка пересечения DK и грани ABC: 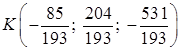
7) Угол 
правляющими векторами прямых AB и BC: 
и 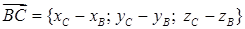

по формуле(54):
Тогда угол между ребрами AB и BC:
8) Чтобы определить угол 
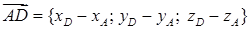
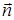
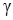
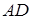
 |
Тогда угол между ребром AD и гранью ABC:
9) Выполним чертеж пирамиды в системе координат (рис. 19).
1)
2) АВС:
3) 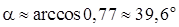
4)
5) DK: 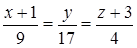
6) 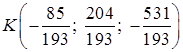
7) 
8) 
9) чертеж пирамиды на рис. 19.
Варианты контрольнЫХ работ
Каждый вариант контрольной работы № 1 для студентов-заочников
1 курса всех специальностей содержит 5 задач, охватывающих материал по теме «Аналитическая геометрия на плоскости». Каждый вариант контрольной работы № 2 содержит 4 задачи по темам «Элементы линейной алгебры. Аналитическая геометрия в пространстве».
Перед выполнением каждой контрольной работы студенту необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии с методическими указаниями, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.
Задания для всех вариантов общие; студенту следует выбрать из условия каждой задачи данные, необходимые для ее решения, в соответствии со своим вариантом. Оформление контрольных работ должно соответствовать установленным правилам и требованиям. Необходимые чертежи должны выполняться четко, с соответствующими подписями и комментариями (см. образец выполнения примерного варианта работы).
Варианты контрольной работы № 1
Задача 1. Даны координаты вершин треугольника АВС.
| Номер варианта | Координаты точек | Номер варианта | Координаты точек |
| А(–2; –3), В(2; 7), С(6; –1) | А(3; –3), В(–4; 1), С(–2; 5) | ||
| А(–5; 1), В(6; 3), С(–4; –7) | А(3; 5), В(–2; 2), С(2; –4) | ||
| А(4; 5), В(–3; 2), С(5; –4) | А(–2; 4), В(5; 6), С(3; –4) | ||
| А(7; –7), В(1; 2), С(–5; –4) | А(3; 7), В(–4; 1), С(–2; –5) | ||
| А(–3; 4), В(4; 5), С(8; –3) | А(4; 3), В(–3; –2), С(–7; 2) |
1) вычислить длину стороны ВС;
2) составить уравнение стороны ВС;
3) найти внутренний угол треугольника при вершине В;
4) составить уравнение высоты АК, проведенной из вершины А;
5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан);
6) сделать чертеж в системе координат.
Задача 2. Даны координаты точки А, уравнение прямой l и число λ.
| Номер варианта | Координаты точки | Уравнение прямой l | Число λ | Номер варианта | Координаты точки | Уравнение прямой l | Число λ |
| А(–1; 0) | y + 2 = 0 | 1 : 1 | А(–5; 1) | x + 1 = 0 | 1: 1 | ||
| А(3; 1) | 3x = 16 | 3 : 4 | А(5; –4) | 5x = 1 | 5 : 1 | ||
| А(3; 0) | x = 0 | 2 : 1 | А(1; 0) | 2x = 7 | 2 : 3 | ||
| А(2; 0) | 4x = 1 | 4 : 3 | А(1; 2) | x = 4 | 1 : 2 | ||
| А(0; 0) | 2x + 5 = 0 | 2 : 3 | А(3; 2) | 3x = 1 | 3 : 1 |
Найти уравнение траектории точки М, которая движется в плоскости так, что отношение ее расстояний до точки А и до прямой l равно λ. Сделать чертеж в системе координат.
Задача 3. Дано уравнение кривой 2-го порядка.
| Номер варианта | Уравнение кривой | Номер варианта | Уравнение кривой |
| 7x 2 – 9y 2 + 42x+ 18y – 9 = 0 | 9x 2 + 4y 2 – 54x + 8y + 49 = 0 | ||
| x 2 + 2x – 12y + 37 = 0 | x 2 – 10x + 4y + 17 = 0 | ||
| 5x 2 + 9y 2 + 10x – 54y + 41 = 0 | 3x 2 – y 2 – 30x – 2y + 62 = 0 | ||
| y 2 + 6x + 6y – 3 = 0 | y 2 – 8x – 4y – 4 = 0 | ||
| 5x 2 – 4y 2 – 20x – 24y – 36 = 0 | 7x 2 + 16y 2 – 56x + 64y + 64 = 0 |
Привести заданное уравнение к каноническому виду путем параллельного переноса осей координат. Определить тип кривой, найти ее характерные элементы в исходной системе координат. Изобразить на чертеже расположение кривой относительно обеих систем координат.
Задача 4. Даны уравнение кривой 2-го порядка и уравнение прямой.
| Номер варианта | Уравнение кривой | Уравнение прямой |
| x 2 + 2y 2 – 2x + 8y + 3 = 0 | x + 2y + 3 = 0 | |
| x 2 – 2y 2 + 4x + 4y – 6 = 0 | x + 2y = 0 | |
| x 2 + 6x – 16y + 25 = 0 | x – 4y + 15 = 0 | |
| x 2 + 4y 2 – 6x + 8y + 5 = 0 | x – 2y – 5 = 0 | |
| y 2 – 4x – 6y – 15 = 0 | 2x + y – 3 = 0 | |
| x 2 – 5y 2 + 10x + 20y – 15 = 0 | x – 5y + 15 = 0 | |
| x 2 + 4y 2 + 2x – 32y + 45 = 0 | x – y + 5 = 0 | |
| x 2 – 4x + 8y + 44 = 0 | x – 2y – 20 = 0 | |
| 2x 2 – y 2 – 16x – 6y + 19 = 0 | x – y – 7 = 0 | |
| y 2 + 10x + 8y – 34 = 0 | 2x + y + 4 = 0 |
1) привести заданное уравнение кривой 2-го порядка к каноническому виду;
2) найти точки пересечения кривой и заданной прямой;
3) построить обе линии в исходной системе координат.
Задача 5. Дано уравнение кривой в полярной системе координат (ПСК).
| Номер варианта | Уравнение кривой | Номер варианта | Уравнение кривой |
 |  | ||
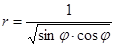 | 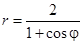 | ||
 | 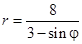 | ||
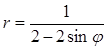 |  | ||
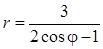 | 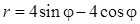 |
1) найти область определения функции 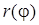
2) построить кривую в ПСК, вычислив значения функции в точках 

3) найти уравнение заданной кривой в декартовой системе координат (ДСК), начало координат в которой совпадает с полюсом ПСК, а положительная полуось ОХ – с полярной осью ОР;
4) определить тип кривой.
Варианты контрольной работы № 2
Задача 1. Даны многочлен f(x) и матрица А.
| Номер варианта | Многочлен f(x) | Матрица А |
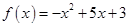 | 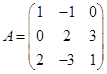 | |
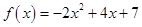 |  |
| Номер варианта | Многочлен f(x) | Матрица А |
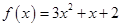 |  | |
 |  | |
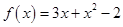 | 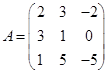 | |
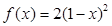 | 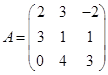 | |
 | 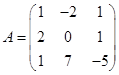 | |
 | 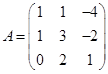 | |
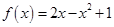 |  | |
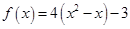 |  |
Требуется найти значение матричного многочлена 
Задача 2. Дана система трех линейных алгебраических уравнений
с тремя неизвестными.
| Номер варианта | Система уравнений | Номер варианта | Система уравнений |
 | 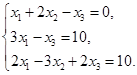 | ||
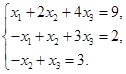 | 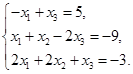 | ||
 | 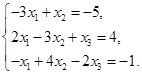 | ||
 | 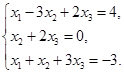 | ||
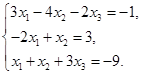 |  |
1) записать систему в матричном виде;
2) найти решение системы с помощью формул Крамера;
3) решить систему при помощи обратной матрицы.
Задача 3. Даны координаты трех векторов 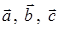

| Номер варианта | Векторы 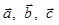 | Вектор 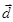 |
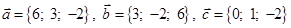 | 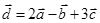 | |
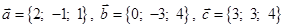 | 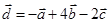 | |
 | 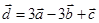 |
| Номер варианта | Векторы 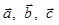 | Вектор 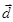 |
 | 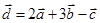 | |
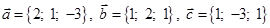 |  | |
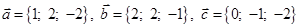 | 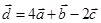 | |
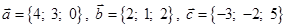 |  | |
 | 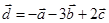 | |
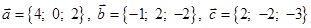 | 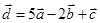 | |
 |  |
1) вычислить модуль вектора 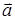
2) найти координаты вектора 
3) найти угол φ между векторами 
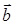
4) вычислить проекцию вектора 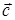
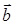
5) вычислить площадь треугольника, построенного на векторах 
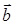
6) вычислить объем параллелепипеда, построенного на векторах 
Задача 4. Даны координаты точек – вершин пирамиды ABCD.
| Номер варианта | Координаты точек |
| А(1; 2; –1), В(0; 0; 1), С(1; –3; 3), D(2; –1; –1) | |
| А(7; 2; 4), В(7; –1; –2), С(3; 3; 1), D(4; 2; 1) | |
| А(1; 3; 6), В(2; 2; 1), С(–1; 0; 1), D(–4; 6; –3) | |
| А(–2; 0; –4), В(–1; 7; 1), С(4; –8; –4), D(1; –4; 6) | |
| А(1; 2; 0), В(3; 0; –1), С(5; –2; 3), D(3; 2; –1) | |
| А(–1; 1; 2), В(2; 1; –2), С(–2; 0; 4), D(2; –1; 2) | |
| А(4; 2; 5), В(2; –3; 0), С(–10; 5; 8), D(–5; 2; 4) | |
| А(2; –1; 1), В(–1; –3; 2), С(–2; 3; 1), D(–1; 2; –3) | |
| А(–1; 1; 2), В(–2; 0; 3), С(3; 6; –3), D(–1; –2; 7) | |
| А(4; –1; 3), В(–2; 1; 0), С(0; –5; 1), D(–2; 1; –1) |
1) вычислить длину ребра AB;
2) найти уравнение плоскости грани ABC;
3) найти угол 
4) составить параметрические уравнения прямой AB;
5) составить канонические уравнения высоты пирамиды DK, проведенной из вершины D;
6) найти координаты точки пересечения DK и грани ABC;
7) найти угол 
8) найти угол 
9) сделать чертеж пирамиды в системе координат.
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. – М. : Айрис-пресс, 2003. – 288 с.
2. Щипачев, В.С. Высшая математика : учебник для вузов / В.С. Щипачев.– М. : Высш. шк., 1998. – 479 с.
3. Данко, П.Е. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 1
/ П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М. : Высш. шк., 1999. – 304 с.
4. Щипачев, В.С. Задачник по высшей математике / В.С. Щипачев. – М. : Высш. шк., 2001. – 304 с.
Налоговая льгота – Общероссийский классификатор продукции
ОК 005-93, т. 2; 95 3004 – воспитательная, образовательная и педагогическая литература
 |
Издательство МГТУ. 183010 Мурманск, Спортивная, 13.
Сдано в набор 14.09.2007. Подписано в печать 18.09.2007. Формат 60´84 1 /16.
Бум. типографская. Усл. печ. л. 2,79. Уч.-изд. л. 2,18. Заказ 443. Тираж 300 экз.
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать  Общее уравнение плоскости : описание, примеры, решение задачВ статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости. Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать  Общее уравнение плоскости: основные сведенияПеред началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат O x y z в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x , y , и z , которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным. Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости. Любую плоскость, заданную в прямоугольной системе координат O x y z трехмерного пространства, можно определить уравнением A x + B y + C z + D = 0 . В свою очередь, любое уравнение A x + B y + C z + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A , B , C , D – некоторые действительные числа, и числа A , B , C не равны одновременно нулю. Теорема состоит из двух частей. Разберем доказательство каждой из них.
Возьмем произвольную точку заданной плоскости M ( x , y , z ) .В таком случае векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю: n → , M 0 M → = A x — x 0 + B ( y — y 0 ) + C ( z — z 0 ) = A x + B y + C z — ( A x 0 + B y 0 + C z 0 ) Примем D = — ( A x 0 + B y 0 + C z 0 ) , тогда уравнение преобразуется в следующий вид: A x + B y + C z + D = 0 . Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
В теореме также указано, что действительные числа А , B , C одновременно не являются равными нулю. Тогда существует некоторая точка M 0 ( x 0 , y 0 , z 0 ) , координаты которой отвечают уравнению A x + B y + C z + D = 0 , т.е. верным будет равенство A x 0 + B y 0 + C z 0 + D = 0 . Отнимем левую и правую части этого равенства от левой и правой частей уравнения A x + B y + C z + D = 0 . Получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 , и оно эквивалентно уравнению A x + B y + C z + D = 0 . Докажем, что уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает некоторую плоскость. Уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n → = ( A , B , C ) и M 0 M → = x — x 0 , y — y 0 , z — z 0 . Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 множество точек M ( x , y , z ) задает плоскость, у которой нормальный вектор n → = ( A , B , C ) . При этом плоскость проходит через точку M ( x 0 , y 0 , z 0 ) . Иначе говоря, уравнение A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) + D = 0 задает в прямоугольной системе координат O x y z трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение A x + B y + C z + D = 0 также определяет эту плоскость. Теорема доказана полностью. Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства. Допустим, задано некоторое общее уравнение плоскости λ · A x + λ · B y + λ · C z + λ · D = 0 , где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением A x + B y + C z + D = 0 , поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства. Раскроем чуть шире смысл теорем. В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида A x + B y + C z + D = 0 ( при конкретных значениях чисел A , B , C , D ). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат. Укажем пример как иллюстрацию этих утверждений. Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4 x + 5 y – 5 z + 20 = 0 , и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4 x + 5 y – 5 z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость. Видео:Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать  Общее уравнение плоскости, проходящей через точкуПовторимся: точка M 0 ( x 0 , y 0 , z 0 ) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением A x + B y + C z + D = 0 в том случае, когда подставив координаты точки M 0 ( x 0 , y 0 , z 0 ) в уравнение A x + B y + C z + D = 0 , мы получим тождество. Заданы точки M 0 ( 1 , — 1 , — 3 ) и N 0 ( 0 , 2 , — 8 ) и плоскость, определяемая уравнением 2 x + 3 y — z — 2 = 0 . Необходимо проверить, принадлежат ли заданные точки заданной плоскости. Решение Подставим координаты точки М 0 в исходной уравнение плоскости: 2 · 1 + 3 · ( — 1 ) — ( — 3 ) — 2 = 0 ⇔ 0 = 0 Мы видим, что получено верное равенство, значит точка M 0 ( 1 , — 1 , — 3 ) принадлежит заданной плоскости. Аналогично проверим точку N 0 . Подставим ее координаты в исходное уравнение: 2 · 0 + 3 · 2 — ( — 8 ) — 2 = 0 ⇔ 12 = 0 Равенство неверно. Таким, образом, точка N 0 ( 0 , 2 , — 8 ) не принадлежит заданной плоскости. Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит. Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n → = ( A , B , C ) — нормальный вектор для плоскости, определяемой уравнением A x + B y + C z + D = 0 . Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости. В прямоугольной системе координат задана плоскость 2 x + 3 y — z + 5 = 0 . Необходимо записать координаты всех нормальных векторов заданной плоскости. Решение Мы знаем, что заданные общим уравнением коэффициенты при переменных x , y , z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n → исходной плоскости имеет координаты 2 , 3 , — 1 . В свою очередь, множество нормальных векторов запишем так: λ · n → = λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0 Ответ: λ · 2 , λ · 3 , — λ , λ ∈ R , λ ≠ 0 Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора. Очевидным фактом является то, что нормальный вектор n → = ( A , B , C ) является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M 0 ( x 0 , y 0 , z 0 ) , принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали. Общее уравнение плоскости с нормальным вектором n → = ( A , B , C ) будет выглядеть так: A x + B y + C z + D = 0 . По условию задачи точка M 0 ( x 0 , y 0 , z 0 ) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство: A x 0 + B y 0 + C z 0 + D = 0 Вычитая соответственно правые и левые части исходного уравнения и уравнения A x 0 + B y 0 + C z 0 + D = 0 , получим уравнение вида A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 . Оно и будет уравнением плоскости, проходящей через точку M 0 ( x 0 , y 0 , z 0 ) и имеющей нормальный вектор n → = ( A , B , C ) . Возможно получить это уравнение другим способом. Очевидным фактом является то, что все точки М ( x , y , z ) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n → = ( A , B , C ) и M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю: n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 Задана точка М 0 ( — 1 , 2 , — 3 ) , через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n → = ( 3 , 7 , — 5 ) . Необходимо записать уравнение заданной плоскости. Решение Рассмотрим два способа решения.
x 0 = — 1 , y 0 = 2 , z 0 = — 3 , A = 3 , B = 7 , C = — 5 Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 3 ( x — ( — 1 ) ) + 7 ( y — 2 ) — 5 ( z — ( — 3 ) ) = 0 ⇔ 3 x + 7 y — 5 z — 26 = 0
M 0 M → = ( x — x 0 , y — y 0 , z — z 0 ) = ( x + 1 , y — 2 , z + 3 ) Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда: n → , M 0 M → = 0 ⇔ 3 ( x + 1 ) + 7 ( y — 2 ) — 5 ( z + 3 ) = 0 ⇔ ⇔ 3 x + 7 y — 5 z — 26 = 0 Ответ: 3 x + 7 y — 5 z — 26 = 0 Видео:2. Уравнение плоскости примеры решения задач #1Скачать  Неполное общее уравнение плоскостиВыше мы говорили о том, что, когда все числа А , B , C , D отличны от нуля, общее уравнение плоскости A x + B y + C z + D = 0 называют полным. В ином случае общее уравнение плоскости является неполным. Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О ( 0 , 0 , 0 ) , то придем к тождеству: A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям O x y , O x z , O y z соответственно и проходят через точки 0 , 0 , — D C , 0 , — D B , 0 и — D A , 0 , 0 соответственно. При D = 0 уравнения самих координатных плоскостей O x y , O x z , O y z выглядят так: z = 0 , y = 0 , x = 0 Задана плоскость, параллельная координатной плоскости O y z и проходящая через точку М 0 ( 7 , — 2 , 3 ) . Необходимо составить общее уравнение заданной плоскости. Решение Условием задачи определено, что заданная плоскость параллельна координатной плоскости O y z , а, следовательно, может быть задана общим неполным уравнением плоскости A x + D = 0 , A ≠ 0 ⇔ x + D A = 0 . Поскольку точка M 0 ( 7 , — 2 , 3 ) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x + D A = 0 , иначе говоря, должно быть верным равенство 7 + D A = 0 . Преобразуем: D A = — 7 , тогда требуемое уравнение имеет вид: x — 7 = 0 . Задачу возможно решить еще одним способом. Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости O y z . Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости O y z : i → = ( 1 , 0 , 0 ) . Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости: A ( x — x 0 ) + B ( y — y 0 ) + C ( z — z 0 ) = 0 ⇔ ⇔ 1 · ( x — 7 ) + 0 · ( y + 2 ) + 0 · ( z — 3 ) = 0 ⇔ ⇔ x — 7 = 0 Ответ: x — 7 = 0 Задана плоскость, перпендикулярная плоскости O x y и проходящая через начало координат и точку М 0 ( — 3 , 1 , 2 ) . Решение Плоскость, которая перпендикулярна координатной плоскости O x y определяется общим неполным уравнением плоскости A x + B y + D = 0 ( А ≠ 0 , В ≠ 0 ) . Условием задачи дано, что плоскость проходит через начало координат, тогда D = 0 и уравнение плоскости принимает вид A x + B y = 0 ⇔ x + B A y = 0 . Найдем значение B A . В исходных данных фигурирует точка М 0 ( — 3 , 1 , 2 ) , координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: — 3 + B A · 1 = 0 , откуда определяем B A = 3 . Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x + 3 y = 0 . 📸 ВидеоЗадача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать  4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать  Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать  Уравнение плоскости через 3 точкиСкачать  Записать уравнение прямой параллельной или перпендикулярной данной.Скачать  Лекция 28. Виды уравнения прямой в пространстве.Скачать  22. Взаимное расположение прямой и плоскости в пространствеСкачать  3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  Расстояние от точки до плоскости / Вывод формулыСкачать  Стереометрия 10 класс. Часть 1 | МатематикаСкачать  Лекция 25. Виды уравнений плоскости в пространстве.Скачать  11 класс, 8 урок, Уравнение плоскостиСкачать  | |