Уравнение плоскости перпендикулярной оси оу (7 видео)

Уравнение плоскости перпендикулярной оси оу

Составить уравнение плоскости, перпендикулярной оси Ox и проходящей через точку A(3, 7, -1).

Так как плоскость перпендикулярна оси Ox, то она параллельна плоскости yOz, а потому ее уравнение имеет вид

Подставляя в это уравнение координаты точки A, получим, что D = -3A. Это значение D подставим в Ax + D = 0 и, сокращая на A, будем иметь окончательно x — 3 = 0.

Содержание

Уравнение плоскости перпендикулярной оси оу
Общее уравнение плоскости
Неполные уравнения плоскости
🌟 Видео

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнение плоскости перпендикулярной оси оу

Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут

Неправильный логин или пароль.

Укажите электронный адрес и пароль.

Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.

Инструкция по изменению пароля отправлена на почту.

Чтобы зарегистрироваться, укажите ваш email и пароль

Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Общее уравнение плоскости

В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн.

Пусть задана произвольная декартова прямоугольная система координат Oxyz. Общим уравнением плоскости называется линейное уравнение вида:

Ax+By+Cz+D=0,

(1)

где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля.

Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.

Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть в пространстве задана плоскость α. Выберем оси Ox и Oy так, чтобы они располагались на плоскости α, а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z=0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z=0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.

Пусть фиксирована произвольная декартова прямоугольная система координат Oxyz. Рассмотрим линейное уравнение (1), где хотя бы один из элементов A , B и C отлично от нуля. Тогда уравнение (1) имеет хотя бы одно решение x₀, y₀, z₀. Действительно. Пусть из коэффициентов A≠0. Возьмем произвольные числа y₀, z₀. Тогда

Уравнение плоскости перпендикулярной оси оу

Таким образом, существует точка M₀(x₀, y₀, z₀), координаты которой удовлетворяют уравнению (1):

Ax₀+By₀+Cz₀+D=0.

(2)

Вычитая из уравнения (1) тождество (2), получим

A(x−x₀)+B(y−y₀)+С(z−z₀)=0,

(3)

которая эквивалентна уравнению (1).

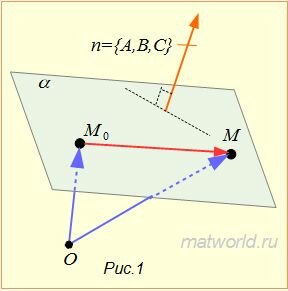Покажем, что (3) определяет некоторую плоскость, проходящую через точку M₀(x₀, y₀, z₀) и перпендикулярную вектору n=<A,B,C> (n≠0, так как хотя бы один из чисел A,B,C отлично от нуля).

Если точка M₀(x₀, y₀, z₀) принадлежит плоскости α, то ее координаты удовлетворяют уравнению (3), т.к. векторы n=<A,B,C> и перпендикулярны (Рис.1) и их скалярное произведение равно нулю:

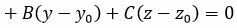Если же точка M(x, y, z) не лежит на плоскости α, то векторы n=<A,B,C> и не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.

Одновременно с доказательством теоремы 1 мы получили следующее утверждение.

Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C) перпендикулярен плоскости Ax+By+Cz+D=0.

Вектор n=(A,B,C) называется нормальным вектором плоскости , определяемой линейным уравнением (1).

Утверждение 2. Если два общих уравнения плоскости

A₁x+B₁y+C₁z+D=0

(4)

A₂x+B₂y+C₂z+D=0

(5)

определяют одну и ту же плоскость, то найдется такое число λ, что выпонены равенства

A₂=A₁λ, B₂=B₁λ, C₂=C₁λ, D₂=D₁λ.

(6)

A₁x₀+B₁y₀+C₁z₀+D=0

(7)

A₂x₀+B₂y₀+C₂z₀+D=0

(8)

Умножая уравнение (7) на λ и вычитая из него уравнение (8) получим:

(A₁λ−A₂)x₀+(B₁λ−B₂)y₀+(C₁λ−C₂)z₀+(D₁λ−D₂)=0.

Так как выполнены первые три равенства из выражений (6), то D₁λ−D₂=0. Т.е. D₂=D₁λ. Утверждение доказано.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Неполные уравнения плоскости

Определение 1. Общее уравнение плоскости (1) называется полным , если все коэффициенты A, B, C, D отличны от нуля. Если же хотя бы один из коэффициентов A, B, C, D равен нулю, то общее уравнение плоскости называется неполным .

Рассмотрим все возможные варианты неполных уравнений плоскости:

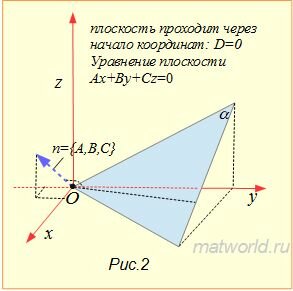
При D=0, имеем уравнение плоскости Ax+By+Cz=0, проходящей через начало координат (Рис.2). Действительно, точка O(0,0,0) удовлетворяет этой системы линейных уравнений.

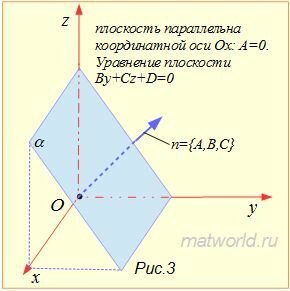
При A=0, имеем уравнение плоскости By+Cz+D=0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n=<0,B,C> лежит на координатной плоскости Oyz.

При B=0, имеем уравнение плоскости Ax+Cz+D=0, которая параллельна оси Oy (Рис.4).

При C=0, имеем уравнение плоскости Ax+By+D=0, которая параллельна оси Oz (Рис.5).

При A=0,B=0 имеем уравнение плоскости Cz+D=0, которая параллельна координатной плоскости Oxy (Рис.6).

При B=0,C=0 имеем уравнение плоскости Ax+D=0, которая параллельна координатной плоскости Oyz (Рис.7).

При A=0,C=0 имеем уравнение плоскости By+D=0, которая параллельна координатной плоскости Oxz (Рис.8).

При A=0,B=0,D=0 имеем уравнение плоскости Cz=0, которая совпадает с координатной плоскостью Oxy (Рис.9).

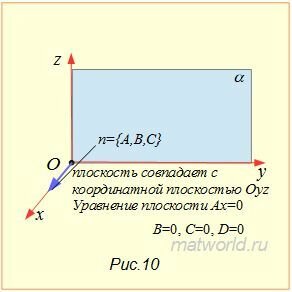
При B=0,C=0,D=0 имеем уравнение плоскости Ax=0, которая совпадает с координатной плоскостью Oyz (Рис.10).

При A=0,C=0,D=0 имеем уравнение плоскости By=0, которая совпадает с координатной плоскостью Oxz (Рис.11).

Рассмотрим примеры построения общего уравнения плоскости.

Пример 1. Построить общее уравнение плоскости, проходящей через точку M(4,−1,2) параллельной координатной плоскости Oxy.

Решение. Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя координаты точки M в (3), получим:

A(x−4)+B(y−(−1))+C(z−2)=0

(9)

Так как плоскость параллельна координатной плоскости Oxy, то направляющий вектор имеет следующий вид n=<A,B,C>=, т.е. A=0, B=0, C=1.

Подставляя коэффициенты A,B,C в (9), получим:

0(x−4)+0(y−(−1))+1(z−2)=0

(9)

Пример 2. Построить общее уравнение плоскости, проходящей через начало координат и имеющий нормальный вектор n==.

Решение. Начало координат имеет коэффициенты (0,0,0). Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя коэффициенты начальной точки в (3), получим:

A(x−0)+B(y−0)+C(z−0)=0

(10)

Так как плоскость имеет нормальный вектор n=<A,B,C>=, т.е. A=2, B=3, C=1, подставляя коэффициенты A,B,C в (10), получим:

2(x−0)+3(y−0)+1(z−0)=0

(9)

Онлайн калькулятор для построения общего уравнения плоскости находится здесь. Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.