Уравнение плоскости и прямой в r3

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

1. Прямые и плоскости в пространстве R n

Изучим пространство R n с другой точки зрения. Будем рассматривать его элементы не как векторы, а как точки, то есть А(х₁, х₂, . х_n), где х_i — координаты точки А ( i = 1, 2, . n). О(0. 0) — назовем началом координат.

Элементы R, R 2 , R 3 можно интерпретировать как координаты точек соответственно на прямой, на плоскости, в пространстве; поэтому R принято называть числовой прямой, R 2 — числовой плоскостью, R 3 — числовым пространством.

Как мы уже знаем, при n>3 непосредственное обращение к геометрии невозможно, но многие факты, относящиеся к R n , носят общий характер, не зависящий от n. Так свойства решений линейных уравнений и методы их исследования не зависят от числа переменных. Тогда можно сказать, что в этом смысле пространство R n обладает геометрическими свойствами, подобными свойствам пространств R, R 2 , R 3 . Множества точек в R 4 (“фигуры”) будем задавать с помощью уравнений, неравенств с n переменными и их систем как области их решений.

Определение 1. Область решений совместной системы линейных уравнений с n переменными ранга r назовем k-мерной плоскостью в R n , где k = n — r (k — число свободных, а r — базисных переменных.)

Отметим два случая:

1. r = n, k = 0. Система имеет единственное решение, которое представляет собой точку в R n , то есть точку можно считать нуль-мерной плоскостью.

2. r = 0, k = n. Все уравнения являются тождествами (0 = 0), все переменные свободные, область решений системы совпадает со всем пространством R n , то есть само пространство можно считать n-мерной плоскостью.

Если этих два крайних случая исключить из рассмотрения, то очевидно, что k может меняться в пределах 1 £ k £ n — 1.

Определение 2. Плоскость наибольшей возможной в R n размерности, но не совпадающей со всем пространством, то есть (n-1)-мерную плоскость, называют гиперплоскостью, а плоскость наименьшей возможной размерности, но не являющуюся точкой, то есть одномерную плоскость, называют прямой.

R — само одномерно и в нем не может быть плоскостей меньшей размерности.

R 2 — (числовая плоскость) — в нем гиперплоскость совпадает с прямой — это одномерная плоскость.

R 3 — (числовое пространство) — здесь гиперплоскостью является двухмерная плоскость, а прямой — одномерная плоскость; других плоскостей нет.

З а м е ч а н и е. При n > 3 кроме гиперплоскостей и прямой существуют плоскости промежуточных размерностей (n-2)-мерные, . трехмерные, двухмерные.

Гиперплоскость обычно задают одним линейным уравнением

в котором не все коэффициенты равны нулю, то есть

. (1.2)

Условие (1.2) равносильно тому, что ранг системы, состоящей из одного уравнения (1.1), равен 1.

Пусть теперь система состоит из двух уравнений

. (1.3)

Если ее матрица А имеет ранг 1, то

В этом случае гиперплоскости, определенные уравнениями системы (1.3), называются параллельными и, если

,

(то есть ранг расширенной матрицы равен 2), то система несовместна:

гиперплоскости, определенные уравнениями системы (1.3), не имеют общих точек (не пересекаются); если же

,

(то есть ранг расширенной матрицы равен 1), то система сводится к одному уравнению, две гиперплоскости совпадают.

И наконец, если ранг матрицы А равен 2, то система определяет (n-2)-мерную плоскость.

Прямую можно задать совместной системой линейных уравнений с n переменными ранга r = n-1. Если известны две точки А(а₁,а₂. а_n), B(b₁,b₂. b_n) прямой, то эту систему можно записать в виде

, (1.4)

где X(x₁, x₂, . x_n) — текущая переменная точка прямой.

Систему уравнений (1.4) называют уравнениями прямой, проходящей через две точки А и В.

1.1. Расстояние от точки до прямой

Рассмотрим прямую l в R 2 , заданную уравнением

А × х + В × у + С = 0

и точку М(х₁,у₁) вне данной прямой.

Обозначим через d расстояние MN (MN перпендикуляр к l). Уравнение перпендикуляра можно записать в виде В × (х — х₁) — А × (у — у₁) = 0.

или

= t, (1.5)

то есть t — коэффициент пропорциональности. Поэтому из (1.5) следует, что

. ×

C другой стороны, точка N(x₂,y₂) принадлежит l, следовательно, из (1.5) получаем

Подставим эти значения в уравнение прямой А × х + В × у + С = 0. Получим

А × х₂ + В × у₂ + С = А × (х₁ + А × t) + В × ( y₁ + В × t) + С = (А × х₁ + В × у₁ + C) + t × (А 2 + В 2 ) = 0

.

.

З а м е ч а н и е. (следствие).

(1.6)

является расстоянием от прямой до начала координат.

2. Разделив обе части общего уравнения прямой на , получим уравнение

, (1.7)

свободный член которого численно равен расстоянию прямой от начала координат. Такое уравнение прямой будем называть нормированным.

1.2. Нормированное уравнение прямой

Пусть дана прямая l. Проведем через начало координат прямую n, перпендикулярную l. Пусть Р — точка пересечения прямых. Возьмем единичный вектор .

Выразим уравнение l через два параметра:

и угол q

Пусть М(х,у) принадлежит l. Тогда проекция на ось, определяемую вектором , равна р, то есть при условии пр_n , так как единичный вектор, то согласно определению скалярного произведения пр_n ,= . Так как , а вектор , то скалярное произведение имеет вид

.

Следовательно, точка М принадлежит прямой l означает, что координаты этой точки удовлетворяют уравнению

. (1.8)

Это и есть нормированное уравнение прямой l.

Пусть теперь имеем общее уравнение прямой l:

l: А × х + В × у + С = 0

l:

t × A = Cos q , t × B = Sin q , t × C = -p.

t 2 × A 2 + t 2 × В 2 = Cos 2 q + Sin 2 q = 1

t 2 × (A 2 + В 2 ) = 1 (1.9)

-нормирующий множитель.

Следовательно, чтобы получить из общего уравнения прямой

А × х + В × у + С = 0

нормированное уравнение (1.8) следует умножить его на нормирующий множитель (1.9), знак которого противоположен С.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

2. Общее уравнение плоскости в R 3

Зафиксируем произвольную декартову прямоугольную систему координат O_xyz и рассмотрим произвольное уравнение первой степени

А × х + В × у + С × z + D = 0, (2.1)

где A, B, C, D — произвольные константы, хотя бы одна из которых не равна 0.

Уравнение (2.1) заведомо имеет хотя бы одно решение (x₀, y₀, z₀).

Действительно, пусть С ¹ 0, следовательно, взяв произвольные (x₀, y₀), мы получим ,

которое эквивалентно (2.1).

Рассмотрим разность между (2.1) и (2.2).

которое эквивалентно (2.1).

Докажем, что уравнение (2.2) и, стало быть, уравнение (2.1), определяет плоскость (П) в O_xyz.

,

то есть хотя бы одна координата его не равна 0.

Возьмем произвольную точку М₀(x, y, z), принадлежащую плоскости П, то есть ее координаты удовлетворяют уравнению (2.3), ибо в этом случае вектор перпендикулярен вектору ( ) и их скалярное произведение

Если точка М(x,y,z) не принадлежит плоскости П, то ее координаты не удовлетворяют (2.3), ибо в этом случае вектор не перпендикулярен вектору и (2.3) не равно нулю.

Таким образом, мы доказали следующее утверждение.

Теорема 2.1. Если в R 3 фиксирована произвольная декартова система координат O_xyz (прямоугольная), то всякое уравнение первой степени с тремя переменными x,y,z определяет относительно этой системы плоскость.

З а м е ч а н и я.

1. Уравнение (2.1) с произвольными коэффициентами А, В, С (хотя бы один из которых не должен быть равен нулю) называется общим уравнением плоскости в R 3 .

2. Если два общих уравнения

А × х + В × у + С × z + D = 0

определяют одну и ту же плоскость, следовательно, существует число t, такое, что справедливы равенства

Рассмотреть(самостоятельно) неполные уравнения плоскости, когда

1) А = 0; 2) В = 0; 3) C = 0; 4) D = 0;

5) A = В = 0; 6) A = C = 0; 7) B = C = 0;

8) A = В = C = 0; 9) A = C = D = 0; 10) В = C = D = 0;

2.1. Угол между двумя плоскостями

Пусть даны две плоскости П₁ и П₂, которые заданы уравнениями

Чтобы определить угол между плоскостями, достаточно определить угол j между их нормальными векторами и .

По определению скалярного произведения

. (2.5)

Условие параллельности двух плоскостей заключается в пропорциональности координат векторов и :

. (2.6)

Условие “плоскость П₁ перпендикулярна к плоскости П₂” определяет, что Cos j = 0

2.2. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой

Пусть даны три точки М₁(x₁,y₁,z₁), М₂(x₂,y₂,z₂) и М₃(x₃,y₃,z₃). Необходимо вывести уравнение плоскости, проходящей через эти три точки. Так как эти три точки не лежат на одной прямой, то векторы и неколлинеарны, и поэтому точка М(x,y,z) лежит в одной плоскости с точками М₁, М₂ и М₃ в том случае, если векторы , и компланарны.

Теорема 2.2. Для того, чтобы три вектора были компланарны, необходимо и достаточно, чтобы выполнялось следующее условие

(2.8)

Из условия (2.8) получим уравнение первой степени относительно x,y,z. Оно и является уравнением искомой плоскости.

2.3. Нормированное уравнение плоскости. Отклонение точки от плоскости

Пусть дана плоскость П. Проведем через начало координат прямую n перпендикуляр к плоскости П, и пусть Р — точка пересечения прямой n и плоскости П.

Рассмотрим вектор и — единичный вектор. . Пусть углы a , b , g образованы с положительными направлениями осей и вектором . Тогда . Очевидно, что точка М(x,y,z) принадлежит плоскости П тогда, когда проекция вектора на ось, определяемую вектором , равна р.

пр_n = р = .

Так как , то скалярное произведение равно р

(2.9)

Определение 2.1. Назовем отклонением d точки М от плоскости П число +d в случае, когда точка М и начало координат точка О лежат по разные стороны от плоскости П, и число -d — в случае, когда точка М и начало координат точка О лежат по одну сторону от плоскости П, (куда направлен вектор — “+d” и “-d” — в противоположном расположении точки М, если точка О лежит на плоскости).

Для нахождения отклонения d точки М₀(x₀,y₀,z₀) от плоскости П следует в левую часть нормированного уравнения плоскости П поставить на место х,у,z координаты x₀,y₀,z₀ точки М.

А × х + В × у + С × z + D = 0

определяют одну ту же плоскость, то существует t такое, что

t × A = Cos a , t × B = Sin b , t × C = Sin g , t × D = -p.

Так как сумма квадратов направляющих косинусов равна 1, то

t 2 × (A 2 + B 2 + C 2 )=1,

, (2.10)

где знак t противоположен знаку коэффициента D.

Для приведения общего уравнения плоскости

А × х + В × у + С × z + D = 0

к нормированному виду (2.9) следует умножить его на нормирующий множитель (2.10), знак которого противоположен знаку коэффициента D.

Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать

3. Прямая линия R 3

Прямую в пространстве R 3 можно задать как пересечение двух плоскостей, определяемых уравнениями

(3.1)

Приведем (3.1) к каноническому виду.

Для этого достаточно найти:

1) хотя бы одну точку М₁(x₁,y₁,z₁), через которую проходит прямая

Так как плоскости, определяемые (3.1), не параллельны и не сливаются, то нарушается (2.6), то есть хотя бы одна из пропорций

,

а это значит, что хотя бы один из определителей второго порядка

, ,

отличен от нуля.

.

Тогда, взяв вместо z произвольное число z₁ и подставив его в уравнение (3.1), можно определить соответственно x₁ и y₁

(3.2)

Можно взять z₁=0. Тогда, воспользовавшись (3.2), получим, что прямая проходит через точку .

Пусть текущая точка М(x,y,z). Тогда уравнение линии можно записать в виде

. (3.3)

. (3.4)

Уравнение прямой, проходящей через данную точку М₁(x₁,y₁,z₁) и перпендикулярной плоскости А × х + В × у + С × z + D = 0, имеет вид

. (3.5)

Уравнение прямой, параллельной данной плоскости и проходящей через данную точку М₀(x₀,y₀,z₀).

Пусть плоскость П задана уравнением

Тогда уравнение прямой имеет вид

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

4. Выпуклые множества точек на плоскости. Неравенства

4.1. Неравенства

Пусть задана линия

то есть это множество точек, координаты которых удовлетворяют этому уравнению. Аналогично можно рассмотреть множество точек, координаты которых удовлетворяют неравенству

(х — a) 2 + (у — b) 2 — r 2 = 0

Это уравнение определяет окружность с центром в точке С(a,b) радиуса r, (Рис. 8.4);

(х — a) 2 + (х — b) 2 — r 2 0

определяет множество точек, лежащих внутри круга с центром в точке С(a,b) радиуса r, (Рис. 8.5);

(х — a) 2 + (х — b) 2 — r 2 > 0

определяет множество точек, лежащих вне этого круга с центром в точке С(a,b) радиуса r (Рис. 8.6);

Множество точек, удовлетворяющих (4.1), называют областью решений этого уравнения.

Аналогично будем говорить об области решений неравенств (4.2) и (4.3).

Пусть теперь F(x, y) — линейное уравнение, то есть имеет вид

F(x, y) = A × x + B × y + C, (4.4)

где A, B, C — константы .

Любое невырожденное уравнение A × x + B × y + C = 0 определяет линию L в R 2 , рассмотрим

A × x + B × y + C 0 (4.5)

A × x + B × y + C > 0, (4.6)

По отношению к прямой линии все точки разбились на два множества Ф₁ и Ф₂, лежащие по разные стороны от прямой L (Рис 8.7).

Покажем, что эти множества определяются неравенствами (4.5) и (4.6).

Так как эти точки не лежат на прямой, то имеем

Действительно, так как точки М₁(х₁,у₁), М₂(х₂,у₂) лежат по разные стороны от прямой (4.4), то существует точка М₀(х₀,у₀) такая, что она делит отрезок М₁М₂ в отношении , а сама точка М₀(х₀,у₀) принадлежит прямой L, то есть

, . (4.7)

Так как точка М₀(х₀,у₀) принадлежит прямой L, то имеем

Подставим (4.7) в (4.4):

.

то есть d ₁+ l × d ₂ = 0, откуда d ₁ = -l × d ₂ , но l > 0, следовательно, d ₁ и d ₂ имеют разные знаки.

Пусть, например, d ₁ 0, d ₂ > 0, тогда точка М₁(х₁,у₁) удовлетворяет неравенству (4.5), а точка М₂(х₂,у₂) — неравенству (4.6).

Множество точек, лежащих на некоторой прямой и по одну сторону от нее, называют полуплоскостью.

Очевидно, что каждая прямая L разбивает плоскость П на две полуплоскости, для которых она является общей границей. Считается, что граница принадлежит сразу двум полуплоскостям.

Если (4.4) — это граница, то нестрогие неравенства

A × x + B × y + C £ 0

A × x + B × y + C ³ 0

Пусть задана система неравенств

(4.8)

Геометрически система (4.8) может быть истолкована как область решений этой системы, то есть это множество точек , которые одновременно удовлетворяют всем неравенствам этой системы, то есть . Очевидно, что область решений системы неравенств является пересечением областей решений каждого из неравенств системы.

З а м е ч а н и е. В частности может иметь место .

Областью решений системы линейных неравенств

(4.9)

является очевидно пересечение полуплоскостей, определяемых каждым из неравенств.

Эту область будем называть многоугольником.

Не исключены также случаи вырождения многоугольной области в прямую или луч, а многоугольника — в отрезок или точку.

4.2. Выпуклые множества точек на плоскости

Определение 4.1. Множество точек называется выпуклым, если вместе с двумя его точками М₁ и М₂ ему принадлежат и все внутренние точки отрезка М₁М₂.

Выпуклые множества: полуплоскость, круг, отрезок и так далее.

Многоугольники могут быть как выпуклые, так и невыпуклые. Геометрически это можно всегда увидеть, но этот факт также может быть

установлен и аналитически.

Теорема 4.1. Пусть дана полуплоскость

Ф₁: A × x + B × y + C 0

Если А × х₀ + В × у₀ + С 0, то тогда полуплоскость будет выпуклой.

Д о к а з а т е л ь с т в о :

Координаты точки М₁ можно выразить через координаты точек М₁ и М₂:

, ,

Подставим эти выражения в неравенство полуплоскости

.

l > 0, и по условию

а по определению 8.4 такое множество называется выпуклым.

З а м е ч а н и е. Определение выпуклого множества сформулировано в предположении, что в этом множестве имеются по крайней мере две точки. Если множество пустое (в этом случае его обозначают как Æ ) или состоит из одной точки, то его тоже считают выпуклым.

Для выпуклых множеств имеет место следующая теорема:

Теорема 4.2. Пересечение любого числа выпуклых множеств — выпуклое множество.

Д о к а з а т е л ь с т в о :

Пусть j ₁, j ₂, . j _n — выпуклые множества и их пересечение , тогда оно выпукло. Из того, что точка М₀(х₀,у₀) принадлежит множеству j _i (i = 1. n) следует, что М₀(х₀,у₀) принадлежит .

Пусть имеем две произвольные точки М₁(х₁,у₁) и М₂(х₂,у₂), принадлежащие пересечению множеств j _i, тогда, так как все множества j _i выпуклы, то им принадлежит и отрезок М₁М₂, а следовательно, , но тогда и пересечение есть множество выпуклое.

Следствие. Область решений системы линейных неравенств (), если она не представляет собой Æ , является выпуклой многоугольной областью или выпуклым многоугольником.

Видео:11. Прямая в пространстве и ее уравненияСкачать

5. Выпуклые множества в пространстве. Неравенства

По аналогии с пространством R 2 можно рассмотреть геометрию и неравенства в пространстве R 3 .

определяют множество точек пространства, координаты которых удовлетворяют этим неравенствам.

(х — a) 2 + (х — b) 2 + (z — c) 2 2

определяет внутреннюю область шара, ограниченную сферой

(х — a) 2 + (х — b) 2 + (z — c) 2 = r 2

с центром в точке С(а,b,c) и радиусом r, а неравенство

(х — a) 2 + (х — b) 2 + (z — c) 2 > r 2

определяет множество точек, находящихся вне этого шара.

Множество точек, лежащих в некоторой плоскости и по одну сторону от нее, называют полупространством.

5.1. Нестрогие линейные неравенства

D + A × x + B × y + C × z и

D + A × x + B × y + C × z > 0

определяют два полупространства, общей границей которых будет плоскость

D + A × x + B × y + C × z = 0.

Доказательство этого факта проводится так же, как и в случае двух переменных.

Пусть дана система линейных неравенств с тремя неизвестными

. (5.3)

Областью решений системы (5.3) является пересечение полупространств, то есть такое множество точек, если оно не пусто, которое является решением каждого из неравенств системы. Это пересечение полупространств называют многогранной областью или (в случае ограниченности) многогранником.

З а м е ч а н и е.

1. Понятие выпуклого множества точек и теорема о выпуклости пересечения выпуклых множеств точек сохраняет силу и для пространства.

(Провести доказательство самостоятельно).

2. Так как полупространство выпукло, то область решений системы линейных неравенств (5.3), если она не пуста, является выпуклой многогранной областью (или выпуклым многогранником), если она ограничена.

Не исключены случаи вырождения.

Назад Далее

Видео:3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать

Уравнения прямых и плоскостей

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Поверхности и линии первого порядка.

Уравнение первой степени, или линейное уравнение, связывающее координаты точки в пространстве, имеет вид
$$
Ax+By+Cz+D = 0,label
$$
причем предполагается, что коэффициенты при переменных не равны нулю одновременно, то есть (A^+B^+C^ neq 0). Аналогично, линейное уравнение, связывающее координаты точки на плоскости, — это уравнение
$$
Ax+By+C = 0,label
$$
при условии (A^+B^ neq 0).

В школьном курсе доказывается, что в декартовой прямоугольной системе координат уравнения eqref и eqref определяют соответственно плоскость и прямую линию на плоскости. Из теорем о порядке алгебраических линий и поверхностей следует, что то же самое верно и в общей декартовой системе координат. Точнее, имеют место следующие теоремы.

В общей декартовой системе координат в пространстве каждая плоскость может быть задана линейным уравнением
$$
Ax+By+Cz+D = 0.nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат определяет плоскость.

В общей декартовой системе координат на плоскости каждая прямая может быть задана линейным уравнением
$$
Ax+By+C = 0,nonumber
$$
Обратно, каждое линейное уравнение в общей декартовой системе координат на плоскости определяет прямую.

Эти теоремы полностью решают вопрос об уравнениях плоскости и прямой линии на плоскости. Однако ввиду важности этих уравнений мы рассмотрим их в других формах. При этом будут получены независимые доказательства теорем этого пункта.

Видео:5. Нормальное уравнение плоскости выводСкачать

Параметрические уравнения прямой и плоскости.

Мы будем предполагать, что задана декартова система координат в пространстве (или на плоскости, если мы изучаем прямую в планиметрии). Это, в частности, означает, что каждой точке сопоставлен ее радиус-вектор относительно начала координат.

Рис. 6.1

Вектор (overrightarrow<M_M> = boldsymbol-boldsymbol_), начало которого лежит на прямой, параллелен прямой тогда и только тогда, когда (M) также лежит на прямой. В этом и только этом случае для точки (M) найдется такое число (t), что
$$
boldsymbol-boldsymbol_ = tboldsymbol.label
$$

Наоборот, какое бы число мы ни подставили в формулу eqref в качестве (t), вектор (boldsymbol) в этой формуле определит некоторую точку на прямой.

Уравнение eqref называется векторным параметрическим уравнением прямой, а переменная величина (t), принимающая любые вещественные значения, называется параметром.

Векторное параметрическое уравнение выглядит одинаково и в планиметрии, и в стереометрии, но при разложении по базису оно сводится к двум или трем скалярным уравнениям, смотря по тому, сколько векторов составляют базис.

Получим теперь параметрические уравнения плоскости. Обозначим через (boldsymbol

) и (boldsymbol) ее направляющие векторы, а через (boldsymbol_) — радиус-вектор ее начальной точки (M_). Пусть точка (M) с радиус-вектором (boldsymbol) — произвольная точка пространства (рис. 6.2).

Рис. 6.2

Вектор (overrightarrow<M_M> = boldsymbol-boldsymbol_), начало которого лежит на плоскости, параллелен ей тогда и только тогда, когда его конец (M) также лежит на плоскости. Так как (boldsymbol

) и (boldsymbol) не коллинеарны, в этом и только этом случае (boldsymbol-boldsymbol_) может быть по ним разложен. Поэтому, если точка (M) лежит в плоскости (и только в этом случае), найдутся такие числа (t_) и (t_), что
$$
boldsymbol-boldsymbol_ = t_boldsymbol

+t_boldsymbol.label
$$

Это уравнение называется параметрическим уравнением плоскости. Каждой точке плоскости оно сопоставляет значения двух параметров (t_) и (t_). Наоборот, какие бы числа мы ни подставили как значения (t_) и (t_), уравнение eqref определит некоторую точку плоскости.

Пусть ((x, y, z)) и ((x_, y_, z_)) — координаты точек (M) и (M_) соответственно, а векторы (boldsymbol

) и (boldsymbol) имеют компоненты ((p_, p_, p_)) и ((q_, q_, q_)). Тогда, раскладывая по базису обе части уравнения eqref, мы получим параметрические уравнения плоскости
$$
x-x_ = t_p_+t_q_, y-y_ = t_p_+t_q_, z-z_ = t_p_+t_q_.label
$$

Отметим, что начальная точка и направляющий вектор прямой образуют на ней ее внутреннюю декартову систему координат. Значение параметра (t), соответствующее какой-то точке, является координатой этой точки во внутренней системе координат. Точно так же на плоскости начальная точка и направляющие векторы составляют внутреннюю систему координат, а значения параметров, соответствующие точке, — это ее координаты в этой системе.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Прямая линия на плоскости.

Поэтому мы можем сформулировать следующее утверждение.

В любой декартовой системе координат на плоскости уравнение прямой с начальной точкой (M_(x_, y_)) и направляющим вектором (boldsymbol(a_, a_)) может быть записано в виде eqref.

Уравнение eqref линейное. Действительно, после преобразования оно принимает вид (a_x-a_y+(a_y_-a_x_) = 0), то есть (Ax+By+C = 0), где (A = a_), (B = -a_) и (C = a_y_-a_x_).

Вектор с координатами ((-B, A)) можно принять за направляющий вектор прямой с уравнением eqref в общей декартовой системе координат, а точку eqref за начальную точку.

Если система координат декартова прямоугольная, то вектор (boldsymbol(A, B)) перпендикулярен прямой с уравнением eqref.

Действительно, в этом случае ((boldsymbol, boldsymbol) = -BA+AB = 0).

Пусть в уравнении прямой (Ax+By+C = 0) коэффициент (B) отличен от нуля. Это означает, что отлична от нуля первая компонента направляющего вектора, и прямая не параллельна оси ординат. В этом случае уравнение прямой можно представить в виде
$$
y = kx+b,label
$$
где (k = -A/B), а (b = -C/B). Мы видим, что к равно отношению компонент направляющего вектора: (k = a_/a_) (рис. 6.3).

Рис. 6.3. k=-1. Прямая y=-x+1/2

Отношение компонент направляющего вектора (a_/a_) называется угловым коэффициентом прямой.

Угловой коэффициент прямой в декартовой прямоугольной системе координат равен тангенсу угла, который прямая образует с осью абсцисс. Угол этот отсчитывается от оси абсцисс в направлении кратчайшего поворота от (boldsymbol_) к (boldsymbol_) (рис. 6.4).

Рис. 6.4. (k=operatornamevarphi = -1). Прямая (y=-x+1/2)

Положив (x = 0) в уравнении eqref, получаем (y = b). Это означает, что свободный член уравнения (b) является ординатой точки пересечения прямой с осью ординат.

Если же в уравнении прямой (B = 0) и ее уравнение нельзя представить в виде eqref, то обязательно (A neq 0). В этом случае прямая параллельна оси ординат и ее уравнению можно придать вид (x = x_), где (x_ = -C/A) — абсцисса точки пересечения прямой с осью абсцисс.

Видео:Лекция 25. Виды уравнений плоскости в пространстве.Скачать

Векторные уравнения плоскости и прямой.

Параметрическое уравнение плоскости утверждает, что точка (M) лежит на плоскости тогда и только тогда, когда разность ее радиус-вектора и радиус-вектора начальной точки (M_) компланарна направляющим векторам (boldsymbol

) и (boldsymbol). Эту компланарность можно выразить и равенством
$$
(boldsymbol-boldsymbol_, boldsymbol

, boldsymbol) = 0.label
$$
Вектор (boldsymbol = [boldsymbol

, boldsymbol]) — ненулевой вектор, перпендикулярный плоскости. Используя его, мы можем записать уравнение eqref в виде
$$
(boldsymbol-boldsymbol_, boldsymbol) = 0.label
$$

Уравнения eqref и eqref называют векторными уравнениями плоскости. Им можно придать форму, в которую не входит радиус-вектор начальной точки. Например, положив в eqref (D = -(boldsymbol_, boldsymbol)), получим
$$
(boldsymbol, boldsymbol)+D = 0.label
$$

Для прямой на плоскости можно также написать векторные уравнения, аналогичные eqref и eqref,
$$
(boldsymbol-boldsymbol_, boldsymbol) = 0 mbox (boldsymbol, boldsymbol)+C = 0.nonumber
$$
Первое из них выражает тот факт, что вектор (boldsymbol-boldsymbol_) перпендикулярен ненулевому вектору (boldsymbol), перпендикулярному направляющему вектору (boldsymbol), и потому коллинеарен (boldsymbol).

Пусть (x, y, z) — компоненты вектора (boldsymbol) в общей декартовой системе координат. Тогда скалярное произведение ((boldsymbol-boldsymbol_, boldsymbol)) при (boldsymbol neq 0) записывается линейным многочленом (Ax+By+Cz+D), где ((A^+B^+C^ neq 0)).

Обратно, для любого линейного многочлена найдутся такие векторы (boldsymbol_) и (boldsymbol neq 0), что в заданной общей декартовой системе координат (Ax+By+Cz+D = (boldsymbol-boldsymbol_, boldsymbol)).

Первая часть предложения очевидна: подставим разложение вектора (boldsymbol) по базису в данное скалярное произведение:
$$
(xboldsymbol_+yboldsymbol_+zboldsymbol_-boldsymbol_, boldsymbol),nonumber
$$
раскроем скобки и получим многочлен (Ax+By+Cz+D), в котором (D = -(boldsymbol_, boldsymbol)) и
$$
A = (boldsymbol_, boldsymbol), B = (boldsymbol_, boldsymbol), C = (boldsymbol_, boldsymbol)label
$$
(A), (B) и (C) одновременно не равны нулю, так как ненулевой вектор (boldsymbol) не может быть ортогонален всем векторам базиса.

Для доказательства обратного утверждения найдем сначала вектор (boldsymbol) из равенств eqref, считая (A), (B) и (C) заданными. Из ранее доказанного утверждения 10 следует, что
$$
boldsymbol = frac<A[boldsymbol_, boldsymbol_]><(boldsymbol_, boldsymbol_, boldsymbol_)>+frac<B[boldsymbol_, boldsymbol_]><(boldsymbol_, boldsymbol_, boldsymbol_)>+frac<C[boldsymbol_, boldsymbol_]><(boldsymbol_, boldsymbol_, boldsymbol_)>.label
$$

Вектор (boldsymbol_) должен удовлетворять условию (D = -(boldsymbol_, boldsymbol)). Один из таких векторов можно найти в виде (boldsymbol_ = lambda boldsymbol). Подставляя, видим, что (-lambda(boldsymbol, boldsymbol) = D), откуда (boldsymbol_ = -Dboldsymbol/|boldsymbol|^).

Итак, мы нашли векторы (boldsymbol) и (boldsymbol_) такие, что линейный многочлен записывается в виде
$$
x(boldsymbol_, boldsymbol)+y(boldsymbol_, boldsymbol)+z(boldsymbol_, boldsymbol)-(boldsymbol_, boldsymbol),nonumber
$$
который совпадает с требуемым ((boldsymbol-boldsymbol_, boldsymbol)).

Если система координат декартова прямоугольная, то вектор с компонентами (A), (B), (C) является нормальным вектором для плоскости с уравнением (Ax+By+Cz+D = 0).

Это сразу вытекает из формул eqref и доказанного ранее утверждения о нахождении компонент в ортогональном базисе.

Любые два неколлинеарных вектора, удовлетворяющие уравнению eqref, можно принять за направляющие векторы плоскости.

Утверждение 5 нетрудно доказать и непосредственно, рассматривая координаты вектора, параллельного плоскости, как разности соответствующих координат двух точек, лежащих в плоскости.

Все, сказанное о плоскостях, почти без изменений может быть сказано и о прямых на плоскости. В частности, верно следующее утверждение.

Действительно, (alpha_, alpha_), должны быть пропорциональны компонентам — (B), (A) направляющего вектора прямой.

Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Параллельность плоскостей и прямых на плоскости.

Ниже, говоря о параллельных прямых или плоскостях, мы будем считать, что параллельные плоскости (или прямые) не обязательно различны, то есть что плоскость (прямая) параллельна самой себе.

Прямые линии, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+C = 0, A_x+B_y+C_ = 0,nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число (lambda), что
$$
A_ = lambda A, B_ = lambda B.label
$$

Прямые совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнения eqref выполнено (с тем же (lambda)) равенство
$$
C_ = lambda C.label
$$

Первая часть предложения прямо следует из того, что векторы с компонентами ((-B, A)) и ((-B_, A_)) — направляющие векторы прямых.

Докажем вторую часть. В равенствах eqref и eqref (lambda neq 0), так как коэффициенты в уравнении прямой одновременно нулю не равны. Поэтому, если эти равенства выполнены, уравнения эквивалентны и определяют одну и ту же прямую.

Обратно, пусть прямые параллельны. В силу первой части предложения их уравнения должны иметь вид (Ax+By+C = 0) и (lambda(Ax+By)+C_ = 0) при некотором (lambda). Если, кроме того, существует общая точка (M_(x_, y_)) обеих прямых, то (Ax_+By_+C = 0) и (lambda(Ax_+By_)+C_ = 0). Вычитая одно равенство из другого, получаем (C_ = lambda C), как и требовалось.

Плоскости, задаваемые в общей декартовой системе координат уравнениями
$$
Ax+By+Cz+D = 0, A_x+B_y+C_z+D_ = 0nonumber
$$
параллельны тогда и только тогда, когда соответствующие коэффициенты в их уравнениях пропорциональны, то есть существует такое число (lambda), что
$$
A_ = lambda A, B_ = lambda B, C_ = lambda C.label
$$

Плоскости совпадают в том и только том случае, когда их уравнения пропорциональны, то есть помимо уравнений eqref выполнено (с тем же (lambda)) равенство
$$
D_ = lambda D.label
$$

Если плоскости параллельны, то их нормальные векторы (boldsymbol) и (boldsymbol_) коллинеарны, и существует такое число (lambda), что (boldsymbol_ = lambdaboldsymbol). В силу уравнений eqref (A_ = (boldsymbol_, boldsymbol_) = lambda(boldsymbol_, boldsymbol) = lambda A). Аналогично доказываются и остальные равенства eqref. Обратно, если равенства eqref выполнены, то из формулы eqref следует, что (boldsymbol_ = lambdaboldsymbol). Это доказывает первую часть предложения. Вторая его часть доказывается так же, как вторая часть предложения 7.

Условия eqref выражают не что иное, как коллинеарность векторов с компонентами ((A, B)) и ((A_, B_)). Точно так же условия eqref означают коллинеарность векторов с компонентами ((A, B, C)) и ((A_, B_, C_)). Поэтому согласно ранее доказанным этому и этому утверждениям условие параллельности прямых на плоскости можно записать в виде
$$
begin
A& B\
A_& B_
end
= 0,label
$$
а условие параллельности плоскостей — в виде
$$
begin
B& C\
B_& C_
end =
begin
C& A\
C_& A_
end =
begin
A& B\
A_& B_
end
= 0.label
$$

Утверждению 7 можно придать чисто алгебраическую формулировку, если учесть, что координаты точки пересечения прямых — это решение системы, составленной из их уравнений.

При условии eqref система линейных уравнений
$$
Ax+By+C = 0, A_x+B_y+C_ = 0,nonumber
$$
не имеет решений или имеет бесконечно много решений (в зависимости от (C) и (C_). В последнем случае система равносильна одному из составляющих ее уравнений. Если же
$$
begin
A& B\
A_& B_
end
neq 0.nonumber
$$
то при любых (C) и (C_) система имеет единственное решение ((x, y)).

Видео:17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

Уравнения прямой в пространстве.

Прямая линия в пространстве может быть задана как пересечение двух плоскостей и, следовательно, в общей декартовой системе координат определяется системой уравнений вида
$$
left<begin
Ax+By+Cz+D = 0,\
A_x+B_y+C_z+D_ = 0.
endright.label
$$
Пересечение плоскостей — прямая линия тогда и только тогда, когда они не параллельны, что согласно eqref означает, что хоть один из детерминантов отличен от нуля:
$$
begin
B& C\
B_& C_
end^ +
begin
C& A\
C_& A_
end^ +
begin
A& B\
A_& B_
end^
neq 0.label
$$

Разумеется, систему eqref можно заменить на любую, ей эквивалентную. При этом прямая будет представлена как пересечение двух других проходящих через нее плоскостей.

Вспомним параметрические уравнения прямой eqref. Допустим, что в них ни одна из компонент направляющего вектора не равна нулю. Тогда
$$
t = frac<x-x_><alpha_>, t = frac<y-y_><alpha_>, t = frac<z-z_><alpha_>,nonumber
$$
и мы получаем два равенства
$$
frac<y-y_><alpha_> = frac<z-z_><alpha_>, frac<x-x_><alpha_> = frac<z-z_><alpha_>,label
$$
или, в более симметричном виде,
$$
frac<x-x_><alpha_> = frac<y-y_><alpha_> = frac<z-z_><alpha_>,label
$$
Уравнения eqref представляют прямую как линию пересечения двух плоскостей, первая из которых параллельна оси абсцисс (в ее уравнение не входит переменная (x)), а вторая параллельна оси ординат.

Если обращается в нуль одна из компонент направляющего вектора, например, (alpha_), то уравнения прямой принимают вид
$$
x = x_, frac<y-y_><alpha_> = frac<z-z_><alpha_>,label
$$
Эта прямая лежит в плоскости (x = x_) и, следовательно, параллельна плоскости (x = 0). Аналогично пишутся уравнения прямой, если в нуль обращается не (alpha_), а другая компонента.

Когда равны нулю две компоненты направляющего вектора, например, (alpha_) и (alpha_), то прямая имеет уравнения
$$
x = x_, y = y_.label
$$
Такая прямая параллельна одной из осей координат, в нашем случае — оси аппликат.

Важно уметь находить начальную точку и направляющий вектор прямой, заданной системой линейных уравнений eqref. По условию eqref один из детерминантов отличен от нуля. Допустим для определенности, что (AB_-A_B neq 0). В силу утверждения 9 при любом фиксированном (z) система уравнений будет иметь единственное решение ((x, y)), в котором (x) и (y), разумеется, зависят от (z). Они — линейные многочлены от (z): (x = alpha_z+beta_), (y = alpha_z+beta_).

Не будем доказывать этого, хотя это и не трудно сделать. Для ясности, заменяя (z) на (t), получаем параметрические уравнения прямой
$$
x = alpha_t+beta_, y = alpha_t+beta_, z = t.nonumber
$$

Первые две координаты начальной точки прямой (M_(beta_, beta_, 0)) можно получить, решая систему eqref при значении (z = 0).

Из параметрических уравнений видно, что в этом случае направляющий вектор имеет координаты ((alpha_, alpha_, 1)). Найдем его компоненты в общем виде. Если система координат декартова прямоугольная, векторы с компонентами ((A, B, C)) и (A_, B_, C_) перпендикулярны соответствующим плоскостям, а потому их векторное произведение параллельно прямой eqref, по которой плоскости пересекаются. Вычисляя векторное произведение в ортонормированном базисе, мы получаем компоненты направляющего вектора
$$
begin
B& C\
B_& C_
end,
begin
C& A\
C_& A_
end,
begin
A& B\
A_& B_
end.label
$$

Вектор с компонентами eqref есть направляющий вектор прямой с уравнениями eqref, какова бы ни была декартова система координат.

Согласно утверждению 5 каждый ненулевой вектор, компоненты которого ((alpha_, alpha_, alpha_)) удовлетворяют уравнению (Aalpha_+Balpha_+Calpha_ = 0), параллелен плоскости с уравнением (Ax+By+Cz+D = 0). Если, кроме того, он удовлетворяет уравнению (A_alpha_+B_alpha_+C_alpha_ = 0), то он параллелен и второй плоскости, то есть может быть принят за направляющий вектор прямой. Вектор с компонентами eqref ненулевой в силу неравенства eqref. Непосредственно легко проверить, что его компоненты удовлетворяют обоим написанным выше условиям. На этом доказательство заканчивается.

Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Уравнение плоскости, виды уравнения плоскости

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Видео:Уравнение плоскости через 3 точкиСкачать

Определение уравнения плоскости

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х , у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Видео:Уравнение плоскости. 11 класс.Скачать

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А , В , С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А , В , С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ — это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Общим уравнениям плоскости x — 2 · y + 3 · z — 7 = 0 и — 2 · x + 4 · y — 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А , B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y — 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x — y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А , В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = ( A , B , C ) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z — p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ — это направляющие косинусы нормального вектора данной плоскости единичной длины.

n → = ( cos α , cos β , cos γ ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = ( cos α , cos β , cos γ ) . Если p равно нулю, то плоскость проходит через начало координат.

Плоскость задана общим уравнением плоскости вида — 1 4 · x — 3 4 · y + 6 4 · z — 7 = 0 . D = — 7 ≤ 0 , нормальный вектор этой плоскости n → = — 1 4 , — 3 4 , 6 4 имеет длину, равную единице, так как n → = — 1 4 2 + — 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

Видео:Найти уравнение плоскости проходящей через прямую и перпендикулярно плоскостиСкачать

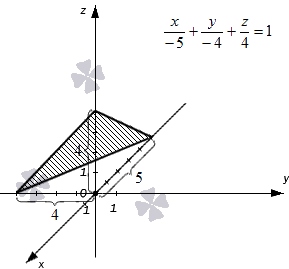
Уравнение плоскости в отрезках

Плоскость отсекает на координатных осях O х , O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с . Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а , b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x — 5 + y — 4 + z 4 = 1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.

📺 Видео

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Видеоурок "Уравнение плоскости по трем точкам"Скачать