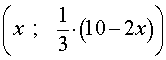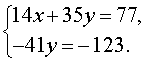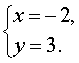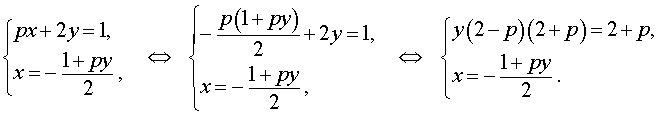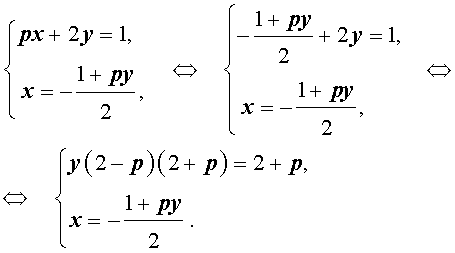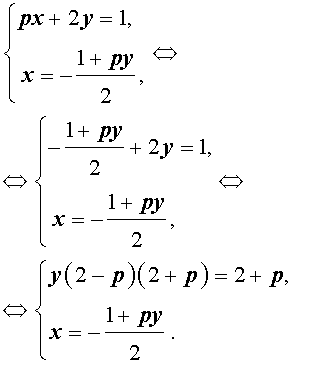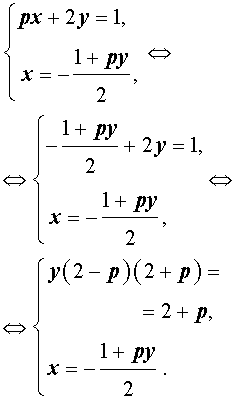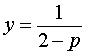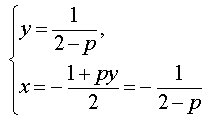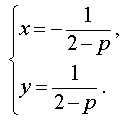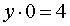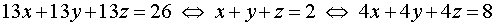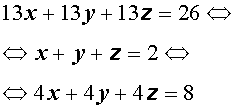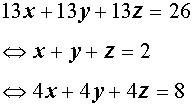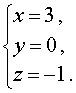Уравнение первой степени с двумя неизвестными называется уравнение вида ax by c (3 видео)

Линейное уравнение первой степени с двумя переменными

Линейное уравнение первой степени с двумя переменными.

Линейное уравнение первой степени с двумя переменными – это уравнение вида ax + by = c, где x и y – неизвестные, a, b, c – некоторые числа, при этом хотя бы одно из чисел a и b не равно нулю. Числа a и b называются коэффициентами при неизвестных, c – свободным членом.

Подобное определение не всегда сразу понятно, и, безусловно, требует дополнительных разъяснений. Попробуем объяснить.

Что означает уравнение с двумя переменными?

Тут все просто. Это уравнение, в котором присутствует сразу два неизвестных числа. Для какой задачи мы можем использовать подобную математическую модель? Например, в 7 Б классе учатся 18 человек. Причем неизвестно, сколько девочек и сколько мальчиков. Пусть мальчиков будет x, а девочек y. Таким образом, у нас получается такое уравнение:
x + y = 18. Заметим, что у нас много вариантов значений x и y, при которых наше уравнение обратится в верное числовое равенство. Например, x = 10, y = 8 или x = 5, y = 13 и т.д.

Такую пару чисел, при которой уравнение с двумя переменными обращается в верное равенство, называют решением уравнения. К примеру, x = 2 и y = 16 – решение уравнения x + y = 18. Это решение можно записать и в кратком виде — (2; 16). Важно при этом соблюдать порядок записи чисел. В уравнении вида ax + by = c решение записывается именно в таком порядке – (x; y). То есть сначала x, потом y.

Насколько много решений у уравнения с двумя переменными?

Обычно, если коэффициенты a и b не равны нулю, решений уравнения с двумя переменными бесконечное множество. Действительно, если подставлять в уравнение значения x, всегда можно будет определить соответствующее значение y, при котором уравнение обратится в верное равенство. Но бывает и такое, когда уравнение с двумя переменными не имеет решений. Такое возможно, когда, например, коэффициенты a и b равны нулю, а свободный член c ≠ 0.

Что означает уравнение первой степени?

Это означает что степень, в которую возводятся переменные этого уравнения – 1. То есть, у нас нет в уравнении переменных, которые мы возводим в квадрат, куб, четвертую степень, извлекаем корень и т.д.

Что означает линейное уравнение?

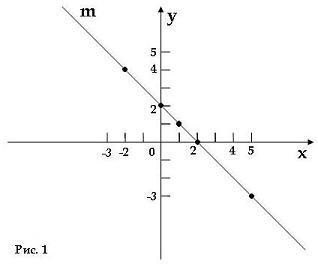
Линейное уравнение – это уравнение прямой линии. В этом легко убедиться, вспомнив понятие координатной плоскости. Мы знаем, что каждой паре чисел соответствует единственная точка на координатной плоскости. Теперь возьмем, к примеру, уравнение x + y = 2. Во множество решений данного уравнения попадают такие пары чисел: (0; 2), (2; 0), (1; 1), (5; -3), (-2; 4). Построим эти точки и проведем через них прямую m.

Мы получили график прямой m. Каждая точка этой прямой имеет координаты, являющиеся решением уравнения x + y = 2, или еще говорят, что каждая точка удовлетворяет уравнению x + y = 2. Вообще для того чтобы построить прямую, достаточно найти 2 пары чисел, удовлетворяющих линейному уравнению. И через точки с данными координатами можно строить прямую.

Содержание

Алгебра. 7 класс
Системы линейных уравнений
Линейные уравнения (уравнения первой степени) с двумя неизвестными
Системы из двух линейных уравнений с двумя неизвестными
Системы из трех линейных уравнений с тремя неизвестными
📹 Видео

Видео:Алгебра 7 класс (Урок№45 - Уравнения первой степени с двумя неизвестными.)Скачать

Алгебра. 7 класс

Уравнения первой степени с двумя неизвестными

Математические термины

Стандартный вид

Определение

Значение переменной

Необходимо запомнить

Уравнение вида $ax + by =c$, где $x$ и $y$ – неизвестные и свободный член c – любые действительные числа, называется линейным уравнением с двумя неизвестными.

$ax + by =c$ – нормальный вид такого уравнения.

Каждая пара значений x и y, удовлетворяющая уравнению с двумя неизвестными, называется решением этого уравнения.

Линейное уравнение с двумя неизвестными обычно имеет бесконечное множество решений и поэтому называется неопределенным уравнением.

Если в уравнении первой степени с двумя неизвестными коэффициент при y равен нулю, то получим уравнение с одним неизвестным ($x$). Например:

Графиком последнего уравнения, а поэтому и двух других равносильных ему уравнений, является прямая, параллельная оси ординат.

Итак, графиком уравнения $ax + by = c$, если $a$ и $b$ не равны нулю одновременно, является прямая линия. Ее обычно строят по точкам пересечения с осями координат. Если $a = 0$ и $b = 0$, то возможны два случая:

1) $0x + 0y =17$ или $0 = 17$ – уравнение не имеет ни одного решения и ему не удовлетворяют координаты ни одной точки плоскости;

2) $0x + 0y = 0$ или $0 = 0$ – уравнение имеет бесчисленное множество решений (причём значения $x$ и $y$ здесь даже не зависят друг от друга) и ему удовлетворяют координаты всех точек плоскости.

Задача на составление неопределенного уравнения

Трёхногие инопланетяне выгуливают на лужайке своих двуногих питомцев. Кто-то подсчитал, сколько ног ходит по лужайке. Их оказалось $15$. Сколько было инопланетян и сколько их питомцев?

Необходимо ввести две переменные: $x$ – число инопланетян, $y$ – число питомцев, тогда получим уравнение $3x + 2y = 15$.

Давайте же узнаем сколько инопланетян выгуливало своих питомцев.

$3x + 2y = 15$. Выразим y через $x$: $y=frac$, далее воспользуемся методом перебора: при $x = 1$, $y = 6$, при $x = 2$, $y: notin : N$ , при $x = 3$, $y = 3$.

Ответ: $1$ инопланетянин и $6$ питомцев; $3$ инопланетянина и $3$ питомца.

Подобные уравнения встречаются часто, они-то и называются неопределенными. Особенность их состоит в том, что уравнение содержит две или более переменных и требуется найти все целые или натуральные их решения. Такими уравнениями и занимался Диофант. Он изобрел большое число способов решения подобных уравнений, поэтому их часто называют диофантовыми уравнениями.

Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Системы линейных уравнений

Уравнение первой степени с двумя неизвестными называется уравнение вида ax by c

Линейные уравнения (уравнения первой степени) с двумя неизвестными

Системы из двух линейных уравнений с двумя неизвестными

Системы из трех линейных уравнений с тремя неизвестными

Видео:Уравнения первой степени с двумя неизвестнымиСкачать

Линейные уравнения (уравнения первой степени) с двумя неизвестными

Определение 1 . Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид

ax +by = c ,

(1)

где a , b , c – заданные числа.

Определение 2 . Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.

Пример 1 . Найти решение уравнения

2x +3y = 10

(2)

Решение . Выразим из равенства (2) переменную y через переменную x :

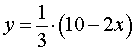(3)

Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида

где x – любое число.

Замечание . Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).

Видео:Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

Системы из двух линейных уравнений с двумя неизвестными

Определение 3 . Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид

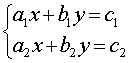(4)

Определение 4 . В системе уравнений (4) числа a₁ , b₁ , a₂ , b₂ называют коэффициентами при неизвестных , а числа c₁ , c₂ – свободными членами .

Определение 5 . Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).

Определение 6 . Две системы уравнений называют равносильными (эквивалентными) , если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.

Равносильность систем уравнений обозначают, используя символ «»

Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных , который мы проиллюстрируем на примерах.

Пример 2 . Решить систему уравнений

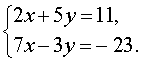(5)

Решение . Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х .

С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.

Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид

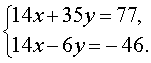(6)

Теперь совершим над системой (6) следующие преобразования:

первое уравнение системы оставим без изменений;
из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.

В результате система (6) преобразуется в равносильную ей систему

Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем

Пример 3 . Найти все значения параметра p , при которых система уравнений

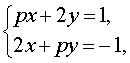(7)

а) имеет единственное решение;

б) имеет бесконечно много решений;

в) не имеет решений.

Решение . Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим

Следовательно, система (7) равносильна системе

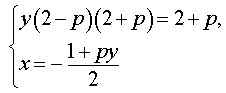(8)

Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):

y (2 – p) (2 + p) = 2 + p

(9)

Если , то уравнение (9) имеет единственное решение

Следовательно, система (8) равносильна системе

Таким образом, в случае, когда , система (7) имеет единственное решение

Если p = – 2 , то уравнение (9) принимает вид

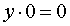
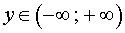
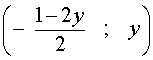
и его решением является любое число . Поэтому решением системы (7) служит бесконечное множество всех пар чисел

где y – любое число.

Если p = 2 , то уравнение (9) принимает вид

и решений не имеет, откуда вытекает, что и система (7) решений не имеет.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Системы из трех линейных уравнений с тремя неизвестными

Определение 7 . Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид

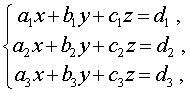(10)

Определение 9 . Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.

Пример 4 . Решить систему уравнений

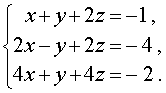(11)

Решение . Будем решать систему (11) при помощи метода последовательного исключения неизвестных .

Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:

первое уравнение системы оставим без изменений;
ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.

В результате система (11) преобразуется в равносильную ей систему

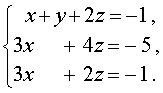(12)

Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:

первое и второе уравнения системы оставим без изменений;
из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.

В результате система (12) преобразуется в равносильную ей систему

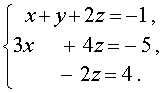(13)

Из системы (13) последовательно находим

Пример 5 . Решить систему уравнений

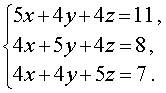(14)

Решение . Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:

Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):

Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.

Замечание . Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».