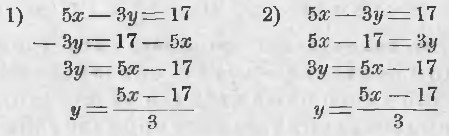Уравнение первой степени с двумя неизвестными 8 букв кроссворд ответ (2 видео)

Математика

55. Уравнение с двумя неизвестными. Рассмотрим теперь уравнение

Оно является записью задачи: найти числовые значения для x и y, чтобы двучлен 5x + 3y оказался равным числу 18.

Мы знаем, что если бы в этом двучлене было бы лишь одно неизвестное число, то и тогда мы сумели бы решить соответствующее уравнение. Поэтому возникает соображение, что здесь одно из неизвестных является как бы лишним: если взамен неизвестного y, например, взять какое угодно число, то мы получим уравнение с одним неизвестным.

А если так, то данное уравнение должно иметь сколько угодно решений, и выясняется способ их получения: станем давать одному из неизвестных, например, y, произвольные значения и всякий раз из получаемого уравнения с 1 неизвестным станем определять другое неизвестное x. Чтобы придать этой работе больше порядка, будем результаты ее записывать в таблице.

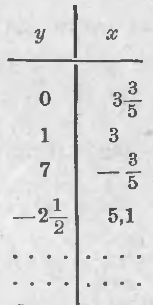
Дадим y значение 0, т. е. примем, что y = 0 (записано в первой строчке таблицы). Тогда наше уравнение обратится в

(в таблице записываем это число во втором столбце, озаглавленном буквою x).

Итак, мы получили одно решение нашего уравнения: y = 0 и x = 3(3/5) (если эти значения подставить в наш двучлен вместо x и y, то требование, чтобы двучлен равнялся числу 18, оправдается:
3 * 3(3/5) + 3 * 0 = 18).

Дадим y значение 1, т. е. примем, что y = 1 (вторая строчка таблицы); тогда получим

откуда 5x = 18 – 3 или 5x = 15 и x = 3 (записано во 2-ой строчке). Итак, найдено второе решение уравнения y = 1 и x = 3.

Дадим y значение 7, т. е. примем, что y = 7; тогда получим уравнение 5x + 21 = 18, откуда 5x = –3 и x = –3/5 (см. 3-ю строчку таблицы).

Примем еще y = –2½; тогда 5x + 3(–2½) = 18 или 5x – 7½ = 18, откуда 5x = 25½ и x = 5(1/10) = 5,1 (см. 4-ю строчку таблицы). Эту работу можно продолжить сколь угодно далеко. Итак, одно уравнение с двумя неизвестными имеет бесконечно много решений; для их получения надо одному неизвестному давать произвольные значения и из получаемых уравнений определять всякий раз другое неизвестное .

Рассматривая предыдущую таблицу и вспоминая п. 49, мы установим: у нас y был независимым переменным, x — зависимым, или x является функцией y – a.

Мы можем несколько ускорить работу нахождения решений данного уравнения. Сочтем y за известное число (все равно, ведь, y мы всякий раз заменяли известным числом); тогда на уравнение 5x + 3y = 18 мы можем смотреть, как на уравнение с одним неизвестным x и решим это уравнение:

5x = 18 – 3y; x = (18 – 3y) / 5

Мы можем этот результат выразить словами так: мы из данного уравнения определили y через x .

Теперь по формуле (18 – 3y) / 5 мы можем легко найти сколько угодно решений, делая вычисления в уме. Примем, например, y = 2. Тогда надо (–3) умножить на (+2), получим –6; сложить (+18) и (–6) — получим +12 и разделить на 5 — получим x = +2(2/5). Еще пусть y = 10; тогда (–3) · (+10) = –30; (+18) + (–30) = –12; (–12) : (+5) = –2(2/5), т. е. x = –2(2/5) и т. д.

Возьмем еще уравнение:

Примем за независимое переменное x, а за зависимое y и определим y через x. Это можно сделать двумя приемами:

Быть может второй прием удобнее 1-го, так как его выполнение легче поддается воображению, если желательно выполнить определение y-а через x в уме.

Теперь мы можем найти сколько угодно решений нашего уравнения: 1) x = 0; y = –5(2/3); 2) x = 1; y = –4; 3) x = –1; y = –7(1/3) и т. д.

Следует приучиться быстро (в уме) определять одно из неизвестных данного уравнения с двумя неизвестными через другое. Примеры:
f55_3

Содержание

Решение уравнений с двумя неизвестными
Определение
Решение задач
Система уравнений с двумя неизвестными
Метод подстановки
Метод сложения
Графический метод
Видео
Алгебра. 7 класс
Степень уравнения
Видео

Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Решение уравнений с двумя неизвестными

В математике большая часть задач ориентирована на решение стандартных уравнений, в которых представлена одна переменная. Однако, некоторые из них, помимо числовых выражений, содержат одновременно две неизвестные. Перед тем как приступить к решению такого уравнения, стоит изучить его определение.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Определение

Итак, уравнением с двумя неизвестными называют любое равенство следующего типа:

a*x + b*y =с, где a, b, c — числа, x, y — неизвестные переменные.

Ниже приведены несколько примеров:

Уравнение с двумя неизвестными точно так же, как и с одной, имеет решение. Однако такие выражения, как правило, имеют бесконечное множество разных решений, поэтому в алгебре их принято называть неопределенными.

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Решение задач

Чтобы решить подобные задачи, необходимо отыскать любую пару значений x и y, которая удовлетворяла бы его, другими словами, обращала бы уравнение с неизвестными x и y в правильное числовое равенство. Найти удовлетворяющую пару чисел можно при помощи метода подбора.

Для наглядности объяснений подберем корни для выражения: y-x = 6.

При y=5 и x=-1 равенство становится верным тождеством 5- (-1) = 6. Поэтому пару чисел (-1; 5) можно считать корнями выражения y-x = 6. Ответ: (-1; 5).

Необходимо отметить, что записывать полученный ответ по правилам необходимо в скобках через точку с запятой. Первым указывается значение х, вторым — значение y.

У равенств такого вида может и не быть корней. Рассмотрим такой случай на следующем примере: x+y = x+y+9

Приведем исходное равенство к следующему виду:

В результате мы видим ошибочное равенство, следовательно, это выражение не имеет корней.

При решении уравнений можно пользоваться его свойствами. Первое их них: каждое слагаемое можно вынести в другую часть выражения. Вместе с этим обязательно нужно поменять знак на обратный. Получившееся равенство будет равнозначно исходному.

Например, из выражения 20y — 3x = 16 перенесем неизвестное y в другую его часть.

Оба равенства равносильны.

Второе свойство: допустимо умножать или делить части выражения на одинаковое число, не равное нолю. В итоге получившиеся равенства будут равнозначны.

Оба уравнения также равносильны.

Видео:Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

Система уравнений с двумя неизвестными

Система уравнений представляет собой некоторое количество равенств, выполняющихся одновременно. В большинстве задач приходится находить решение системы, состоящей из двух равенств с двумя переменными.

Для решения системы уравнений необходимо найти пару чисел, обращающих оба уравнения системы в правильное равенство. Решением может служить одна пара чисел, несколько пар чисел или вовсе их отсутствие.

Решить подобные системы уравнений можно, применяя следующие методы.

Метод подстановки

Выражаем неизвестное из любого равенства через вторую переменную.
Подставляем получившееся выражение неизвестного во второе равенство и решаем его.
Делаем подстановку полученного значения неизвестного и вычисляем значение второго неизвестного.

Метод сложения

Приводим к равенству модули чисел при каком-либо неизвестном.
Производим вычисление одной из переменных, произведя сложение или вычитание полученных выражений.
Подставляем найденное значение в какое-либо уравнение в первоначальной системе и вычисляем вторую переменную.

Графический метод

Выражаем в каждом равенстве одну переменную через другую.
Строим графики двух имеющихся уравнений в одной координатной плоскости.
Определяем точку их пересечения и ее координаты. На этом шаге у вас может получиться три варианта: графики пересекаются — у системы единственно верный вариант решения; прямые параллельны друг другу — система решений не имеет; графики совпадают — у системы бесконечно много решений.
Делаем проверку, подставив полученные значения в исходную систему равенств.

При нахождении корней у одной системы всеми этими способами у вас обязательно должен получиться одинаковый результат, если вы, конечно, все сделали правильно.

В настоящее время есть возможность решения подобных задач с помощью встроенных средств офисной программы Excel, а также на специализированных онлайн-ресурсах и калькуляторах. С помощью них вы легко можете проверить правильность своих вычислений и результатов.

Надеемся, что наша статья помогла вам в освоении этой базовой темы школьной математики. Если же вы пока не можете справиться с решением уравнений такого вида, не расстраивайтесь. Для понимания и закрепления изученной темы рекомендуется как можно больше практиковаться, и тогда у вас без труда получится решать задачи любой сложности. Желаем вам удачи в покорении математических вершин!

Видео:Решение систем уравнений методом подстановкиСкачать

Видео

Из этого видео вы узнаете, как решать уравнения с двумя неизвестными.

Видео:таблица умножения школаСкачать

Алгебра. 7 класс

Значение переменной

Выберите верный вариант ответа.

Какое значение переменной удовлетворяет уравнению: $4x-2y=14$?

Уравнение с двумя переменными

Выберите верные варианты ответа.

Какие значения переменных удовлетворяют уравнению: $x-2y=13$?

Уравнение и его корни

Сопоставьте уравнения и корни, удовлетворяющие их условию.

Определение

Заполните пропуски в тексте, чтобы получить верные определения.

Уравнением первой степени с называется уравнение вида $ax+by=c$, где $x$ и — , $a$ и $b$ ( при неизвестных, не равные , $c$ ( член) — число.

Видео:Проверь свои знания по математике за 11 классСкачать

Степень уравнения

Кроме разделения уравнений по количеству неизвестных, уравнения также разделяются по степеням неизвестных: уравнения первой степени, уравнения второй степени и так далее.

Чтобы определить степень уравнения, в нём нужно предварительно сделать следующие преобразования:

раскрыть скобки,
освободить уравнение от дробных членов,
перенести все неизвестные члены в одну из частей уравнения,
сделать приведение подобных членов.

После выполнения всех этих преобразований, степень уравнения определяется по следующим правилам:

Степенью уравнения с одним неизвестным называется показатель при неизвестном в том члене уравнения, в котором этот показатель наибольший.

10 — x = 2 — уравнение первой степени с одним неизвестным;

x 2 + 7x = 16 — уравнение второй степени с одним неизвестным;

x 3 = 8 — уравнение третьей степени с одним неизвестным.

Степенью уравнения с несколькими неизвестными называется сумма показателей при неизвестных в том члене уравнения, в котором эта сумма наибольшая.

Для примера возьмём уравнение

Для наглядности расставим показатели первой степени (которые обычно не ставят):

3x 2 y 1 + x 1 y 1 + 25 1 = 0.

Теперь посчитаем суммы показателей для тех членов уравнения, в которых присутствуют неизвестные:

3x 2 y 1 — сумма показателей равна 2 + 1 = 3;

x 1 y 1 — сумма показателей равна 1 + 1 = 2.

Сумма показателей у первого члена уравнения больше, чем у второго, значит, при определении степени уравнения будем ориентироваться на сумму показателей первого члена. Это значит, что про данное уравнение можно сказать, что это уравнение третьей степени с двумя неизвестными.

2xy — x = 25 — уравнение второй степени с двумя неизвестным,

xy 2 — 2xy + 8y = 0 — уравнение третьей степени с двумя неизвестными.