Здравствуйте! При движении газа на пути потока могут встречаться различные сопротивления, имеющие уменьшенные проходные сечения (задвижки, вентили, диафрагмы). Как показывает опыт, после прохождения через сопротивление происходит расширение газа и уменьшение его давления (рис. 1.).
При этом кинетическая энергия газа, затраченная на преодоление сил трения, превращается в теплоту трения. Процесс неравновесного расширения газа без совершения внешней работы при прохождении через местное сопротивление принято называть дросселированием.
Если дросселирование происходит при адиабатном течении, то, согласно уравнению первого закона термодинамики для потока,

Обычно вторые члены в обеих частях этого уравнения малы по сравнению с первыми и, кроме того, скорости до дросселирования ω1 и после дросселирования ω2 мало отличаются друг от друга, поэтому вторыми слагаемыми можно пренебречь. Тогда из уравнения (1) получим i1 — i2. Следовательно, при дросселировании с достаточной для технических расчетов точностью энтальпию газа можно считать постоянной.
Так как энтальпия идеального газа зависит только от температуры: di = cpdT то при дросселировании конечная и начальная температуры равны: Т1 = Т2.
Дросселирование реального газа обычно сопровождается изменением его температуры. Это явление было экспериментально установлено в 1852 г. Джоулем и Томсоном и получило название эффекта Джоуля — Томсона.
Характер изменения температуры в процессе дросселирования определяется начальной температурой газа. При некоторой температуре, которая называется температурой инверсии, температура реального газа в процессе дросселирования, как и идеального, остается постоянной. Если температура реального газа перед дросселированием меньше температуры инверсии, то при дросселировании газ будет охлаждаться. При начальных температурах, превышающих точку инверсии, газы в процессе дросселирования нагреваются.
Температура инверсии зависит от давления, и для каждого значения давления имеются две температуры инверсии, расположенные соответственно в области перегретого пара и в области жидкости. Температуры инверсии всех газов, за исключением водорода и гелия, выше 0° С, поэтому дросселирование газов приводит к снижению их температуры. Это явление используется для сжижения газов с помощью машины Линде, в которой осуществляется многократное сжатие и охлаждение газа с последующим его дросселированием. Для сжижения водорода и гелия требуется предварительно охладить их ниже температуры инверсии.
Процесс дросселирования водяного пара удобно рассчитать с помощью is-диаграммы. Построив на диаграмме линию, соответствующую условию i = const (изоэнтальпу), можно определить конечные и промежуточные значения параметров пара. Процессу дросселирования на рис.2. соответствует линия DE i = const.
Из этого примера видно, что при дросселировании влажного насыщенного пара низкого давления (точка D) его степень сухости x повышается и при большом снижении давления в процессе дросселирования пар становится перегретым. Исп. литература: 1) Теплотехника, под редакцией А.П.Баскакова, Москва, Энергоиздат, 1982. 2) Теплотехника, Бондарев В.А., Процкий А.Е., Гринкевич Р.Н. Минск, изд. 2-е,»Вышейшая школа», 1976.
Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Дросселирование газов и паров
Дросселирование – это эффект падения давления при преодолении потоком рабочего тела сопротивления, например: частично открытого вентиля, задвижки, шибера, пористой стенки (рис. 6.9).
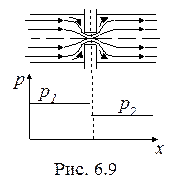
Согласно уравнения первого закона термодинамики (6.2) при 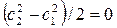
Таким образом, при дросселировании рабочего тела:
· давление уменьшается (dp 0);
· удельный объем увеличивается (dv > 0).
При дросселировании идеального газа температура не изменяется
(dT = 0), т.к. h = f(T).
При дросселировании реальных газов и паров температура может увеличиваться, уменьшаться или не изменяться для одного и того же рабочего тела. Это зависит от параметров, при которых газ либо пар дросселируются.
Изменение температуры реальных газов и паров характеризуется дифференциальным эффектом дросселирования: 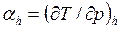
При ah = 0 – температура не изменяется (dT = 0).
Состояние рабочего тела, в котором ah = 0, называется точкой инверсии, а соответствующая ей температура – температурой инверсии (Tинв). При атмосферном давлении для: водорода — tинв = -57 0 С, гелия — tинв = -239 0 С, водяного пара — tинв = 4097 0 С. При температурах t
1. Уясните физический смысл отдельных членов уравнения первого закона термодинамики для потока, поймите разницу между внешней и технической работой, и в каком случае они тождественны.
2. Каково назначение сопел и диффузоров? Как влияет профиль канала на скорость адиабатного потока? Как изменяются параметры в зависимости от изменения скорости (dc>0, dc 2 /с 2 .
4. Уясните особенности истечения с учетом трения: определение параметров действительного процесса, скорости и характерных сечений сопла, расчет потерь кинетической энергии и эксергии.
5. Как изменяются параметры газов и паров при дросселировании? Можно ли этот процесс считать предельным случаем необратимого адиабатного истечения рабочего тела из сопла? Каково практическое применение процессов дросселирования?
Задачи
1. Рассчитайте параметры торможения p0, t0, v0 потока воздуха, имевшего скорость 500 м/с при p =1 бар, t = 30 0 С.
2. Определите параметры торможения (h0, p0) потока сухого насыщенного пара, движущегося со скоростью c = 300 м/с при p =10 бар.
3. Параметры воздуха на входе в сопло равны: p1 = 20 бар, t1 = 300 0 С, скорость c1= 0, давление среды pc = 1 бар.
Рассчитайте скорость (c2) и скорость звука (a2) на выходе из: а) сопла Лаваля; б) суживающегося сопла.
Рассчитывается 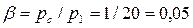
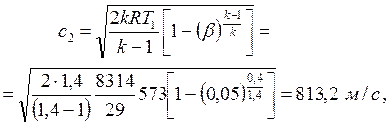  |
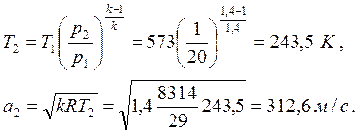  |
В варианте установки суживающегося сопла при b 0 С, истекая из сопла Лаваля, расширяется адиабатно до давления p2 = 1 бар.
Определить площадь выходного и минимального сечений сопла, если массовый расход пара равен G = 4 кг/с.
Выходное и минимальное сечения рассчитываются по уравнениям неразрывности потока (6.31), (6.33):
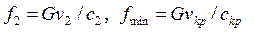 , ,  |
скорости — по формулам:
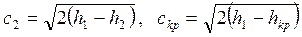 . .  |
Для перегретого пара из табл. 6.1 выбираем bkp = 0,546. Давление пара в минимальном сечении сопла:
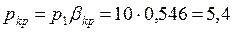 бар. бар.  |
Из h-s- диаграммы для адиабатного процесса расширения находятся необходимые параметры: h1 = 3140 кДж/кг, hkp = 2950 кДж/кг, h2 = 2620 кДж/кг, vkp = 0,44 м 3 /кг, v2 = 1,7 м 3 /кг.
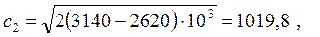 м/с м/с  |
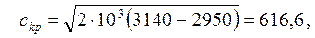
f2 = 4 . 1,7/1019,8 = 6,67 . 10 -3 м 2 ,
fmin =4 . 0,44/616,6 =2,85 . 10 -3 м2
Ответ: f2 = 6,67 . 10 -3 м2 , fmin = 2,85 . 10 -3 м2 .
5. При выпуске из баллона азот дросселируется от исходного состояния, характеризуемого параметрами: p1 = 20 МПа, t1 = 20 0 С, до давления
p2 = 8 МПа.
Определить плотность азота после дросселирования а также изменение энтропии в процессе дросселирования, считая азот идеальным газом, имеющим постоянную теплоемкость.
6. Как изменится температура при дросселировании сухого насыщенного водяного пара с давлением p1= 20 бар до p2 = 1 бар ?
Ответы
1.t0 = 155 0 С, p0 = 1,104 бар, v0 =1,111 м 3 /кг. 2.h0= 2822 кДж/кг,
p0 = 12,5 бар.5. r = 91,95 кг/м 3 , Ds = 0,272 кДж/(кг . К).
ВЛАЖНЫЙ ВОЗДУХ
Влажный воздух – это смесь сухого воздуха и водяного пара.
Давление влажного воздуха равно сумме парциальных давлений сухого воздуха (pс.в.) и водяного пара (pп)
Видео:Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

5.3. Дросселирование
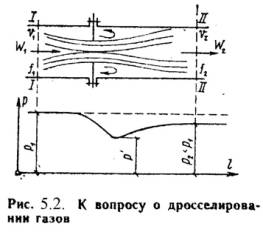
Дросселированием называется явление, при котором пар или газ переходит с высокого давления на низкое без совершения внешней работы и без подвода или отвода теплоты. Такое явление происходит в трубопроводе, где имеется место сужения проходного канала (Рис.5.2). При таком сужении, вследствие сопротивлений, давление за местом сужения — Р2, всегда меньше давления перед ним – Р1.
Любой кран, вентиль, задвижка, клапан и прочие местные сопротивления, уменьшающие проходное сечение трубопровода, вызывают дросселирования газа или пара, следовательно падения давления. В большинстве случаев это явление приносит безусловный вред. Но иногда оно является необходим и создается искусственно (регулирование паровых двигателей, в холодильных установках, в приборах для измерения расхода газа и т.д.).
При прохождении газа через отверстие, кинетическая энергия газа и его скорость в узком сечении возрастают, что сопровождается падением температуры и давления.
Газ, протекая через отверстие, приходит в вихревое движение. Часть его кинетической энергии затрачивается на образование этих вихрей и превращается в теплоту. Кроме того, в теплоту превращается и работа, затраченная на преодоление сопротивлений (трение). Вся эта теплота воспринимается газом, в результате чего температура его изменяется (уменьшается или увеличивается).
В отверстие скорость газа увеличивается. За отверстием газ опять течет по полному сечению и скорость его вновь понижается. А давление увеличивается, но до начального значения оно не поднимается; некоторое изменение скорости произойдет в связи с увеличением удельного объема газа от уменьшения давления.
Дросселирование является необратимым процессом, при которм происходит увеличение энтропии и уменьшение работоспособности рабочего тела.
Уравнением процесса дросселирования является следующее уравнение:i1 = i2 . (5.14)
Это равенство показывает, что энтальпия в результате дросселирования не изменяется и справедливо только для сечений, достаточно удаленных от сужения.
Для идеальных газов энтальпия газа является однозначной функцией температуры. Отсюда следует, что при дросселировании идеального газа его температура не изменяется (Т1 = Т2).
При дросселировании реальных газов энтальпия газа остается постоянной, энтропия и объем увеличиваются, давление падает, а температура изменяется (увеличивается, уменьшается или остется неизменной).
Изменение температуры жидкостей и реальных газов при дросселировании называется эффектом Джоуля-Томсона. Для идеального газа эффект Джоуля-Томсона равен нулю. Различают дифференциальный температурный эффект, когда давление и температура изменяются на бесконечно малую величину, и интегральный температурный эффект, при котором давление и температура изменяются на конечную величину.
Дифференциальный температурный эффект обозначается — б:
Интегральный температурный эффект определяется из следующего уравнения:
Для реальных газов D T ¹ 0 и может иметь положительный или отрицательный знак.
Состояние газа, при котором температурный эффект меняет свой знак, называется точкой инверсии, а температура, соответствующая этой точке, называется температурой инверсии — Тинв.
📽️ Видео
Применение первого начала термодинамики к изопроцессамСкачать

Физика 10 класс (Урок№24 - Первый закон термодинамики.)Скачать

Первый закон термодинамики. 10 класс.Скачать

Физики 10 класс Следствия первого закона термодинамики для различных процессовСкачать

Первый закон термодинамики. Применение первого закона терм-ки к изопроцессам. Практ. ч. 10 класс.Скачать

Физика. 10 класс. Первый закон термодинамики. Применение первого закона термодинамики к изопроцессамСкачать

2.2.5 Применение I закона термодинамики к изопроцессамСкачать

Что такое первый закон термодинамики?Скачать

2 1 Первый закон термодинамики ЭнтальпияСкачать

Урок 170. Количество теплоты. Первый закон термодинамикиСкачать

Тема 13. Первый закон термодинамики. Применение первого закона термодинамики к изопроцессамСкачать

ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ просто | Физика ЕГЭ 10 класс УмскулСкачать

Урок 171. Простейшие задачи на 1-й закон термодинамикиСкачать

ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИСкачать

Первый закон термодинамики | Физика 10 класс #41 | ИнфоурокСкачать

Законы Термодинамики. Что Такое Термодинамика?Скачать