При расчете режима работы электрической цепи очень часто необходимо определить токи, напряжения и мощности на всех ее участках при заданных ЭДС источников и сопротивлений участков цепи. Данный расчёт основан на применении законов Кирхгофа.
В этой статье предполагается, что вы знакомы с определениями узла, ветви и контура.
Содержание:
- Первый закон Кирхгофа
- #1. Запишите выражение для узла В
- #2. Найдите ток i
- Результат
- Выбор направления токов
- Второй закон Кирхгофа.
- Применение второго закона Кирхгофа
- Правила (законы) Кирхгофа простыми словами
- Первое правило Кирхгофа
- Второе правило Киргхофа
- Закон Кирхгофа для магнитной цепи
- Примеры расчета цепей
- Напишите уравнение согласно первому закону Кирхгофа для узла.
- 📹 Видео
Видео:Лекция 117. Правила КирхгофаСкачать

Первый закон Кирхгофа
Первый закон Кирхгофа гласит, что в ветвях образующих узел электрической цепи алгебраическая сумма токов равна нулю (токи входящие в узел считаются положительными, выходящие из узла отрицательными).
Пользуясь этим законом для узла A (рисунок 1) можно записать следующее выражение:

I1 + I2 − I3 + I4 − I5 − I6 = 0.
Попытайтесь самостоятельно применить первый закон Кирхгофа для определения тока в ветви. На приведенной выше схеме изображены шесть ветвей образующие электрический узел В, токи ветвях входят и выходят из узла. Один из токов i неизвестен.
#1. Запишите выражение для узла В
#2. Найдите ток i
Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Результат
Выбор направления токов
Если при расчёте цепи направление токов неизвестны, то при составлении уравнений согласно законом Кирхгофа их необходимо предварительно выбрать произвольно и обозначить на схеме стрелками. В действительности направление токов в ветвях могут отличаться от произвольно выбранных. Поэтому выбранные направления токов называют положительными направлениями. Если в результате расчёта цепи какие-либо токи будут выражены отрицательными числами, то действительные направления этих токов обратны выбранным положительным направлениям.

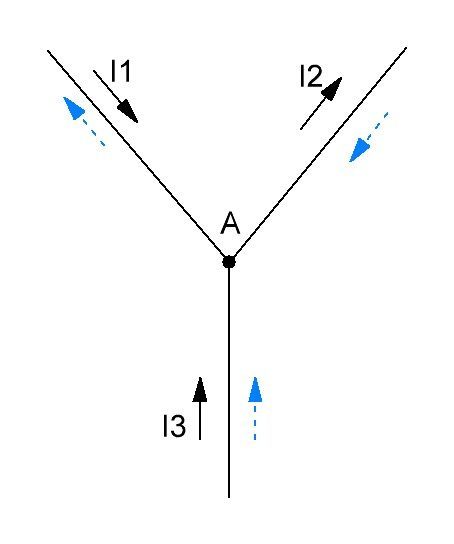
На рисунке 2,а представлен электрический узел. Произвольно, стрелками укажем направления токов (рисунок 2,б).
Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий:
1. Ток должен вытекать из узла через одну или несколько других ветвей;
2. Хотя бы один ток должен входить в узел.
Предположим, что после расчёта цепи получились следующие значения токов:
I1 = -5 А;
I2 = -2 A;
I3 = 3 А.
Так как значение тока I1 и I2 получились отрицательными, следовательно, действительно направление I1 и I2 противоположно ранее выбранным (рисунок 3).
- I1 − I2 + I3 = 0;
- -5 − (-2) +3 = 0;
- -I1 + I2 + I3 = 0;
- -5 + 2 +3 = 0.
Видео:решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

Второй закон Кирхгофа.
Второй закон Кирхгофа: в контуре электрической цепи алгебраическая сумма эдс равна алгебраической сумме падений напряжения на всех сопротивлениях данного контура.
где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.
Применение второго закона Кирхгофа
Для контура ABСDE, изображенного на рисунке 4, стрелками указаны положительные направления токов (произвольно). Составим уравнение согласно второму закону Кирхгофа. Для этого произвольно зададимся направлением обхода контура по часовой или против часовой стрелки. В данном примере направление обхода контура выберем по часовой стрелке.

При составлении уравнений по второму закону Кирхгофа, ЭДС записывается со знаком “+”, если ее направление совпадает с направлением произвольно выбранного обхода контура. В противном случае ЭДС записывается со знаком “-”.
Падения напряжения записываются со знаком “+”, если направление тока в нем совпадает с направлением обхода.
Начнём с эдс E1, так как её направление совпадает с обходом контура — записываем её со знаком “+” перед знаком равно.
Контур ABСDE E1 =
E2 направленна против обхода контура записываем со знаком “-” перед знаком равно.
Контур ABСDE E1 − E2 =
Так как больше ЭДС в контуре ABСDЕ нет — левая часть уравнения готова.
В правой части уравнения указываются падения напряжения контура, так как направления токов I1 и I2 совпадает с обходом контура – записываем падения напряжения со знаком “+”.
Контур ABСDЕE E1 − E2 = I1*R1 + I2*R2
Направление тока I3 не совпадет с обходом контура:
Контур ABСDE E1 − E2 = I1*R1 + I2*R2 − I3*R3.
Уравнение для контура готово.
Законы Кирхгофа являются основой для расчета электрической цепи, вот несколько методов применяющие данные законы.
Видео:Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Правила (законы) Кирхгофа простыми словами
На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.
Учёный Густав Киргхоф сформулировал два правила [1], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.
Видео:Законы Кирхгофа - самое простое и понятное объяснение этих законовСкачать

Первое правило Кирхгофа
Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.
Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.
На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.
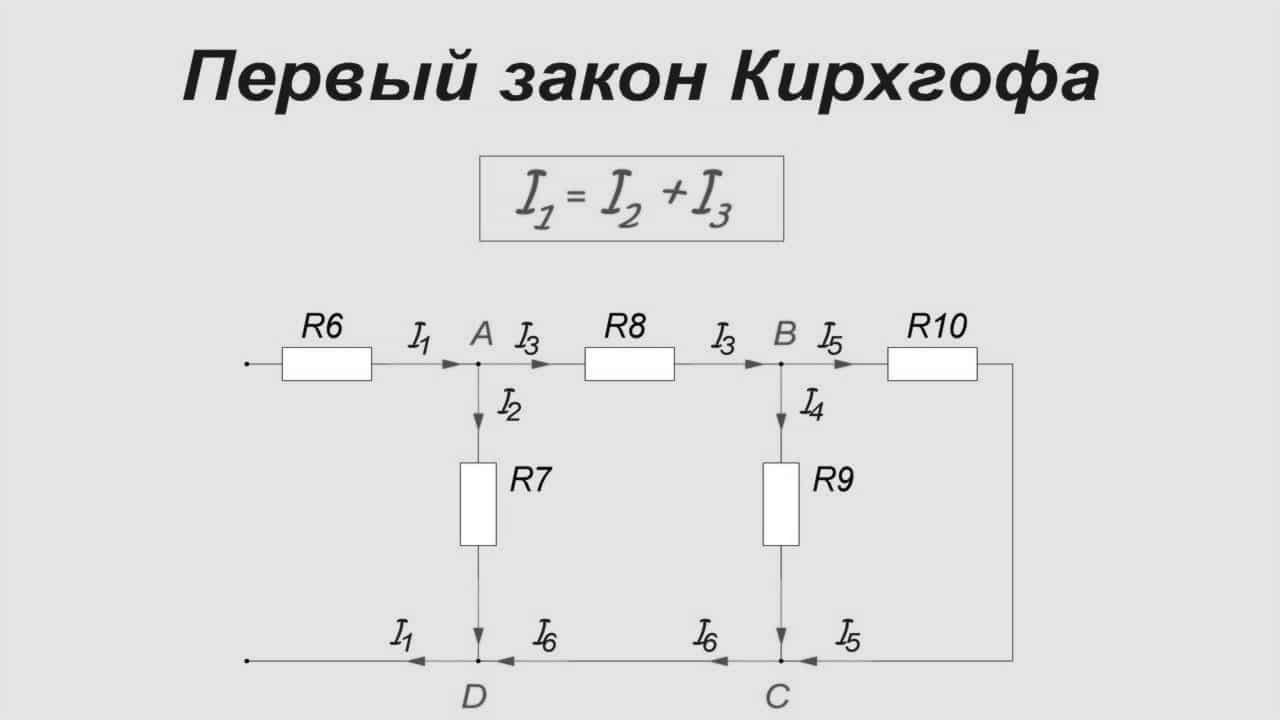
Ток I1 входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I1 = I2 + I3.
На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i1, i2, i3, i4 то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i1 + i2 + i3 + i4 = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.
Запишем наши выводы в алгебраической форме, для общего случая:
Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.
Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.
Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».
Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.
Видео:Как составить уравнения по законам Кирхгофа?Скачать
Второе правило Киргхофа
Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.
Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.
При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.

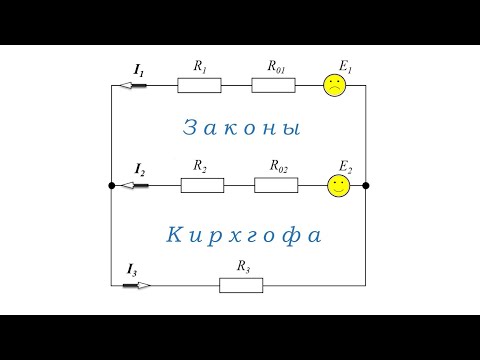
Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.
Формулировки уравнений общего характера:
, где где Lk и Ck – это индуктивности и ёмкости, соответственно.
Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.
Видео:Урок 265. Задачи на правила КирхгофаСкачать

Закон Кирхгофа для магнитной цепи
Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.
То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.
Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).
Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.
Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.
При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».
Видео:Применение законов Кирхгофа при решении задачСкачать

Примеры расчета цепей
Рассмотрим ещё раз рисунок 3. На нём изображено 4 разнонаправленных вектора: i1, i2, i3, i4. Из них – два входящие ( i2, i3) и два исходящие из узла (i1, i4). Положительными будем считать те векторы, которые направлены в точку соединения ветвей, а остальные – отрицательными.
Тогда, по формуле Кирхгофа, составим уравнение и запишем его в следующем виде: – i1 + i2 + i3 – i4 = 0.
На практике такие узлы являются частью контуров, обходя которые можно составить ещё несколько линейных уравнений с этими же неизвестными. Количество уравнений всегда достаточно для решения задачи.
Рассмотрим алгоритм решения на примере рис. 5.

Схема содержит 3 ветви и два узла, которые образуют три пары по два независимых контура:
Запишем независимое уравнение, выполняющееся, например, в точке а. Из первого правила Кирхгофа вытекает: I1 + I2 – I3 = 0.
Воспользуемся вторым правилом Кирхгофа. Для составления уравнений можно выбрать любой из контуров, но нам необходимы контуры с узлом а, так как для него мы уже составили уравнение. Это будут контуры 1 и 2.
Пишем уравнения:
Решаем систему уравнений:
Так как значения R и E известны (см. рисунок 5), мы придём к системе уравнений:
Решая эту систему, получим:
Потенциал узла а равен: Ua = I3*R3 = 3,55 × 3 = 10,65 В. Чтобы убедиться в верности наших расчётов, проверим выполнение второго правила по отношению к контуру 3:
E1 – E2 + I1R1+ I2R2 = 12 – 15 + 1,36 – 4,38 = – 0,02 ≈ 0 (с учётом погрешностей, связанных с округлениями чисел при вычислениях).
Если проверка выполнения второго правила успешно завершена, то расчёты сделаны правильно, а полученные данные являются достоверными.
Применяя правила (законы) Кирхгофа можно вычислять параметры электрической энергии для магнитных цепей.
Видео:Первый закон Кирхгофа! Хочешь понять? Посмотри!Скачать

Напишите уравнение согласно первому закону Кирхгофа для узла.
2.4.4. Нарисуйте в указанном прямоугольнике электрический узел, для которого согласно первому закону Кирхгофа составлено уравнение: I1 + I2 — I3 + I4 — I5— I6 = 0
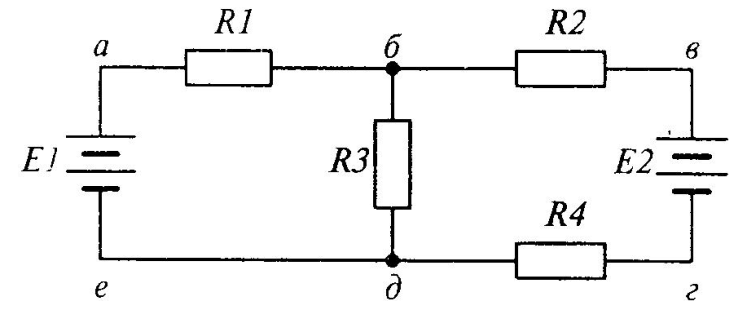

| Дано: | Решение: |
| E1=36B Rг=0.5 Ом E2=30B Rб=0,2 Ом R1=1.5 Ом | E1+E2=I2(R+r)+I,r E1=I,R1 I1= 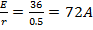 I2= I2= 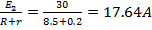 |
| Найти: | |
| Ответ: | 17.64A |
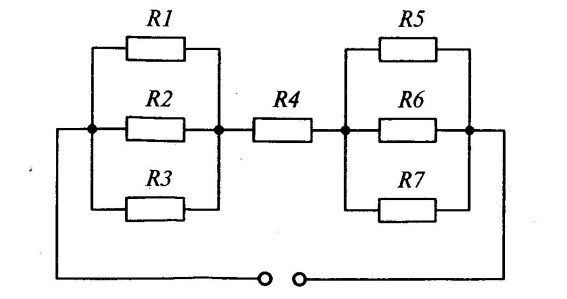
| Дано: | Решение: |
| R1=2 Ом R2=6 Ом R3=18 Ом R4=10 Ом R5=3 Ом R6=9 Ом R7=27 Ом | 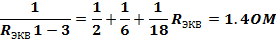 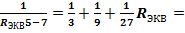 2.08OM 2.08OM  1,4+10+2,08=13,48 OM IОБЩ= 1,4+10+2,08=13,48 OM IОБЩ= 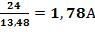 U4=10*1.78=17.8A U4=10*1.78=17.8A |
| Найти: | |
| U4 — ? | |
| Ответ: | 17.8A |
2.4.8. Напряжение сети 12 В. Общий ток, потребляемый четырьмя параллельно включенными одинаковыми лампами, равен 6 А. Определите сопротивление каждой лампы.
| Дано: | Решение: |
| U=12B I=6A |  RЭКВ= RЭКВ= 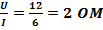 RЭКВ= RЭКВ=  R= RЭКВ*r R=2*4=8 OM-1лампа R= RЭКВ*r R=2*4=8 OM-1лампа |
| Найти: | |
| RA — ? | |
| Ответ: | 8 Ом |
Имеется разветвление, состоящее из четырех параллельно включенных сопротивлений в 10, 5, 3 и 8 Ом. Ток, протекающий к точке разветвления, равен 20 А. Определите ток, протекающий по каждой ветви.
| Дано: | Решение: |
| R1=10 Ом R2=5 Ом R3=3 Ом R4=8 Ом I=20A |  U=I*R=20*1.32=26.4B I1= U=I*R=20*1.32=26.4B I1=  I2= I2= 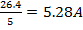 I3= I3= 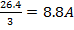 I4= I4=  |
| Найти: | |
| I1-I4 — ? | |
| Ответ: | I1=2.64A, I2=5.28A, I3=8.8A, I4=3.3A |
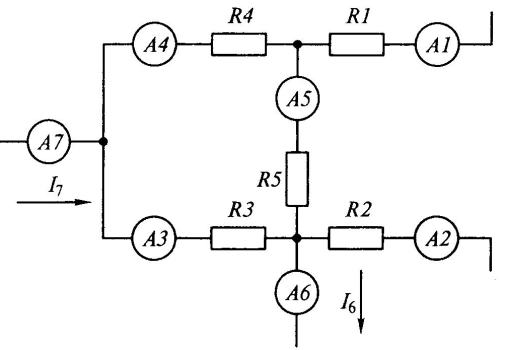
| Дано: | Решение: |
| A7=10A A1=8A A6=1A A5=0A | По закону Кирхгова I4=I1+I5 I4=I1=8A I3=I2+I1+I6 I3=2 I2=1 |
| Найти: | |
| I — ? | |
| Ответ: | I2=1; I3=2 |
2.4.11. Напряжение генератора 110 В. В сеть включены параллельно тридцать ламп сопротивлением по 200 Ом каждая. Определите ЭДС генератора, если его внутреннее сопротивление 0,5 Ом
| Дано: | Решение: |
| R=200 Ом r=0.5 Ом U=110B | I  RЭКВ= RЭКВ= 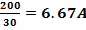 I= I= 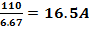 I= I=  |
| Найти:E | |
| Ответ: | 118.3B |
РАБОТА И МОЩНОСТЬ ЭЛЕКТРИЧЕСКОГО ТОКА
2.5.1. Заполните таблицу:
| 55кВт | 1500Вт | 1,5 МВт | 0,33 кВт | 0,12 МВт | 312 кВт |
| 5.5*10 4 Вт | 1.5 кВт | 1.5*10 3 кВт | 330 Вт | 1.2*10 2 кВт | 0.312 МВт |
2.5.2. Определите мощность, потребляемую электрическим двигателем, если ток в цепи равен 6 А, а двигатель включен в сеть напряжением 220 В.
| Дано: | Решение: |
| I=6A U=220B | P=UI P=220*6=1320BT |
| Найти: | |
| P — ? | |
| Ответ: | 1320BT |
На цоколе лампы накаливания написано: 200 Вт, 220 В. Определите сопротивление нити накаливания.
| Дано: | Решение: |
| P=200BT U=220B | P=UI; I= 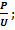 I= I= 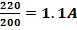 P=I 2 R R= P=I 2 R R= 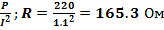 |
| Найти: | |
| R — ? | |
| Ответ: | 165.3 Ом |
2.5.5. Электродвигатель, подключенный к сети 220 В, потребляет ток в 6 А. Какова мощность двигателя и какое количество энергии он потребляет за 8 часов работы?
| Дано: | Решение: |
| U=220B I=6A | P=UI=220*6=1320BT=1.32КВТ/Ч W=PT=1.32*8=10.56КВТ/Ч |
| Найти: | |
| P,W — ? | |
| Ответ: | P=1.32кВт,W=10.56кВт/ч |
2.5.6. В квартире имеется восемь ламп, шесть из них мощностью по 40 Вт горят в сутки по 6 часов, а две мощностью по 60 Вт горят 8 часов в сутки. Сколько нужно заплатить за горение всех ламп в течении месяца (30 дней) при тарифе 120 руб. за 1 кВт час?
| Дано: | Решение: |
| P1-P6=40BT t1=6ч P7-P8=60BT t2=8ч | W=6*40*6+2*60*8=2.4КВТ/Ч WЧАС=2,4*30=72КВТ/Ч D=72*120=8640РУБ |
| Найти: | |
| W — ? | |
| Ответ: | 8640РУБ |
Глава 3 МАГНИТНЫЕ ЦЕПИ
МАГНИТНОЕ ПОЛЕ ТОКА И ЕГО ХАРАКТЕРИСТИКИ
3.1.1. В каких единицах системы СИ измеряются:
магнитная индукция В_ тесла (Тл)
магнитный поток Ф Вебер (Вб)
напряженность магнитного поля Н А/М
индуктивность L Генри (Гн)
3.1.2.Напишите формулы:
а) магнитной индукции б) магнитного потока
B= 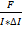
3.1.3. Закончите предложения:
Важное свойство магнитных линий— Замкнутость
Гистерезис — явление которое состоит в том, что физическая величина, характеризующая состояние тела (например, намагниченность) , неоднозначно зависит от физические величины, характеризующей внешние условия (например, магнитного поля)
Ферромагнетики — это вещество, в которых собственные ( внутреннее) магнитное поле может в сотни и тысячи раз превосходить вызывающее его магнитное поле.
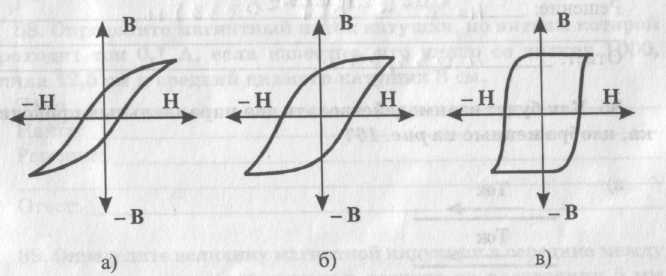
3.1.4. По виду гистерезисных кривых определите тип магнитного материала:
а) магнито- мягкий материал
б)магнито – твердый материал
3.1.5. Запишите формулу закона полного тока:
Что можно определить, применив правило левой руки?
Ответ: определения направления силы, действующей на проводник с током находящимся в магнитном поле.
3.1.7. Магнитная индукция стали 1,5 Тл, площадь поперечного сечения сердечника, изготовленного из этой стали, 0,003 м 2 . Определите магнитный поток, пронизывающий сердечник.
Последнее изменение этой страницы: 2016-04-11; Просмотров: 25533; Нарушение авторского права страницы
📹 Видео
Законы Кирхгофа. Метод контурных уравненийСкачать

Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Метод узловых и контурных уравненийСкачать

Расчет цепи по законам КирхгофаСкачать

Метод контурных токов - определение токов. ЭлектротехникаСкачать

Правило КирхгофаСкачать

Законы Кирхгофа, теория и практическое применениеСкачать

Урок 14. Законы Кирхгофа простыми словами с примерамиСкачать

Электротехника. Расчет цепи с помощью законов Кирхгофа.Скачать

Лекция по темам: "Узел, ветвь и контур . Последовательное и параллельное соединение резисторов"Скачать

ОЛИМПИАДНАЯ ФИЗИКА. Правила КирхгофаСкачать