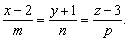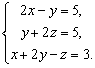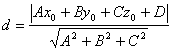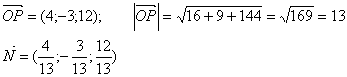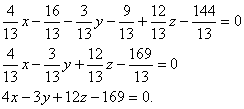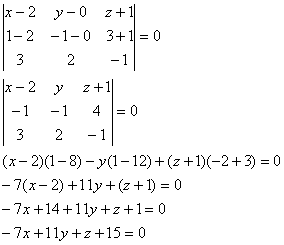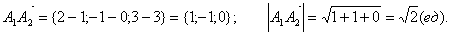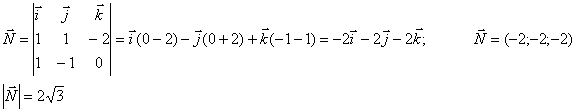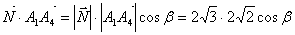Уравнение перпендикуляра опущенного из вершины на плоскость

Прямая и плоскость

Даны канонические уравнения прямой

Пример. Найти проекцию точки А (2; –1; 3) на плоскость x + 2 y – z – 3 =0.

Решение. Проекцию точки А на плоскость найдем как точку пересечения плоскости перпендикуляром, опущенным из точки А на данную плоскость. Составим уравнение перпендикуляра, опущенного из точки А (2; –1; 3) на плоскость x + 2 y – z – 3 = 0:

Из условия перпендикулярности прямой и плоскости имеем ,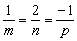

т.е. m = 1, n = 2, p = –1. Уравнения перпендикуляра примут вид

.

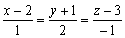
Чтобы найти точку пересечения прямой и плоскости, нужно решить систему из уравнений прямой и плоскости:

или или

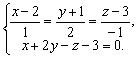
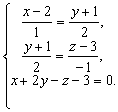
Решая указанную систему, получим координаты проекции точки А на данную плоскость: (3; 1; 2).

Видео:Уравнения прямой на плоскости | Векторная алгебраСкачать

Расстояние от точки до плоскости

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

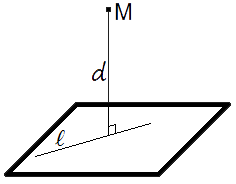
Формула для вычисления расстояния от точки до плоскости

Если задано уравнение плоскости A x + B y + C z + D = 0 , то расстояние от точки M(M _x , M _y , M _z ) до плоскости можно найти, используя следующую формулу:

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Примеры задач на вычисление расстояния от точки до плоскости

Решение. Подставим в формулу коэффициенты плоскости и координаты точки

d = |2·0 + 4·3 + (-4)·6 — 6| √ 4 + 16 + 16 = |0 + 12 — 24 — 6| √ 36 = |-18| 6 = 3

Ответ: расстояние от точки до плоскости равно 3.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнение перпендикуляра опущенного из вершины на плоскость

Расстояние от точки до плоскости .

Расстояние от произвольной точки М₀(х₀, у₀, z ₀ ) до плоскости Ах+Ву+С z + D =0 равно:

Пример. Найти уравнение плоскости, зная, что точка Р(4; -3; 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.

Таким образом, A = 4/13; B = -3/13; C = 12/13, воспользуемся формулой:

Пример. Найти уравнение плоскости, проходящей через две точки P (2; 0; -1) и

Q (1; -1; 3) перпендикулярно плоскости 3х + 2у – z + 5 = 0.

Вектор нормали к плоскости 3х + 2у – z + 5 = 0 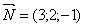параллелен искомой плоскости.

Пример. Найти уравнение плоскости, проходящей через точки А(2, -1, 4) и

В(3, 2, -1) перпендикулярно плоскости х + у + 2 z – 3 = 0.

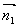
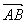
Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0, вектор нормали к этой плоскости ( A , B , C ). Вектор (1, 3, -5) принадлежит плоскости. Заданная нам плоскость, перпендикулярная искомой имеет вектор нормали (1, 1, 2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то

Таким образом, вектор нормали 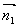(11, -7, -2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е. 11 × 2 + 7 × 1 — 2 × 4 + D = 0; D = -21.

Итого, получаем уравнение плоскости: 11 x — 7 y – 2 z – 21 = 0.

Пример. Найти уравнение плоскости, зная, что точка Р(4, -3, 12) – основание перпендикуляра, опущенного из начала координат на эту плоскость.

Находим координаты вектора нормали 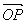= (4, -3, 12). Искомое уравнение плоскости имеет вид: 4 x – 3 y + 12 z + D = 0. Для нахождения коэффициента D подставим в уравнение координаты точки Р:

16 + 9 + 144 + D = 0

Итого, получаем искомое уравнение: 4 x – 3 y + 12 z – 169 = 0

Пример. Даны координаты вершин пирамиды А₁(1; 0; 3), A ₂ (2; -1; 3), A ₃ (2; 1; 1),

Сначала найдем вектор нормали к грани А₁А₂А₃ как векторное произведение векторов и.

= (2-1 ; 1-0; 1-3) = (1; 1; -2);

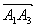
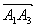
Найдем угол между вектором нормали и вектором .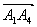

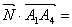
-4 – 4 = -8.

Искомый угол g между вектором и плоскостью будет равен g = 90 0 — b .

5) Найти объем пирамиды.

(ед 3 ).

Воспользуемся формулой уравнения плоскости, проходящей через три точки.

2 x + 2 y + 2 z – 8 = 0

При использовании компьютерной версии “Курса высшей математики” можно запустить программу, которая решит рассмотренный выше пример для любых координат вершин пирамиды.

Угол между плоскостями.

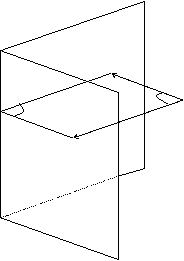Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j ₁ соотношением: j = j ₁ или j = 180 0 — j ₁ , т.е.

cos j = ± cos j ₁ .

Определим угол j ₁ . Известно, что плоскости могут быть заданы соотношениями:

, где

( A ₁ , B ₁ , C ₁ ), ( A ₂ , B ₂ , C ₂ ). Угол между векторами нормали найдем из их скалярного произведения:

.

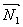
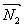
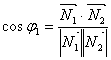
Таким образом, угол между плоскостями находится по формуле:

Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.

Условия параллельности и перпендикулярности

На основе полученной выше формулы для нахождения угла между плоскостями можно найти условия параллельности и перпендикулярности плоскостей.

Для того, чтобы плоскости были перпендикулярны необходимо и достаточно, чтобы косинус угла между плоскостями равнялся нулю. Это условие выполняется, если:

.

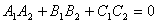
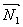
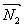
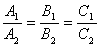
Плоскости параллельны, векторы нормалей коллинеарны: ïï .Это условие выполняется, если: .

🌟 Видео

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Уравнение плоскости. 11 класс.Скачать

Уравнения стороны треугольника и медианыСкачать

10 класс, 19 урок, Расстояние от точки до плоскостиСкачать

Расстояние от точки до плоскости / Вывод формулыСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Видеоурок "Общее уравнение плоскости"Скачать

Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

Вычисляем высоту через координаты вершин 1Скачать

Задача 7. Найти расстояние от точки M0 до плоскости, проходящей через три точки M1, M2, M3.Скачать

Проекция точки на плоскость, проекция прямой на плоскость. Параллельные прямые.Скачать

№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать