С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой («канонический» или «параметрический» ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
- Предупреждение
- Точка пересечения прямой и плоскости − теория, примеры и решения
- 1. Точка пересечения плоскости и прямой, заданной в каноническом виде
- 2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
- 3. Примеры нахождения точки пересечения прямой и плоскости.
- Нахождение уравнений прямой, заданной пересечением двух плоскостей
- Нахождение уравнений прямой, заданной пересечением двух плоскостей
- Канонические уравнения прямой, заданной пересечением двух плоскостей
- Онлайн калькулятор. Уравнение плоскости
- Найти уравнение плоскости
- Ввод данных в калькулятор для составления уравнения плоскости
- Дополнительные возможности калькулятора для вычисления уравнения плоскости
- Теория. Уравнение плоскости.
- 💡 Видео
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Точка пересечения прямой и плоскости − теория, примеры и решения
- Содержание
- 1. Точка пересечения плоскости и прямой, заданной в каноническом виде.
- 2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
- 3. Примеры нахождения точки пересечения прямой и плоскости.
1. Точка пересечения плоскости и прямой, заданной в каноническом виде
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L1:
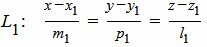 , , | (1) |
| α: Ax+By+Cz+D=0. | (2) |
Найти точку пересечения прямой L1 и плоскости α (Рис.1).
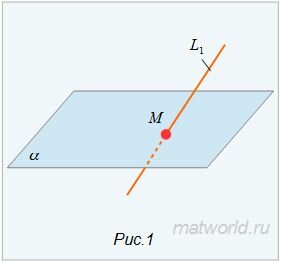 |
Запишем уравнение (1) в виде системы двух линейных уравнений:
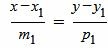 , , | (3) |
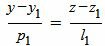 | (4) |
Сделаем перекрестное умножение в уравнениях (3) и (4):
| p1(x−x1)=m1(y−y1) |
| l1(y−y1)=p1(z−z1) |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
| p1x−m1y=p1x1−m1y1, | (5) |
| l1y−p1z=l1y1−p1z1. | (6) |
Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z. Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:
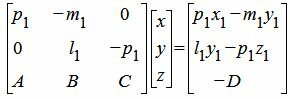 | (7) |
Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L1 и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L1 лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L1 и плоскости α.
Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же
2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L1 в параметрическом виде:
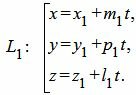 | (8) |
| α: Ax+By+Cz+D=0. | (9) |
Задачу нахождения нахождения точки пересечения прямых L1 и плоскости α можно решить разными методами.
Метод 1. Приведем уравнения прямой L1 к каноническому виду.
Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:
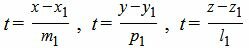 | (10) |
Так как левые части уравнений (10) равны, то можем записать:
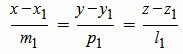 | (11) |
Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.
Метод 2. Для нахождения точки пересечения прямой L1 и плоскости α решим совместно уравнения (8) и (9). Из уравнений (8) подставим x, y, z в (9):
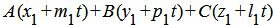 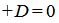 | (13) |
Откроем скобки и найдем t:
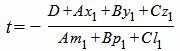 | (14) |
Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L1 лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.
Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L1 и плоскости α подставим полученное значение t из (14) в (8).
3. Примеры нахождения точки пересечения прямой и плоскости.
Пример 1. Найти точку пересечения прямой L1:
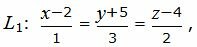 | (15) |
| α: 7x−5y+2z+19=0. | (16) |
Представим уравнение (15) в виде двух уравнений:
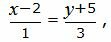 | (17) |
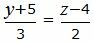 | (18) |
Сделаем перекрестное умножение в уравнениях (17) и (18):
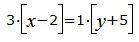 |
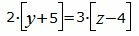 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
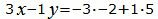 |
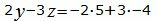 |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):
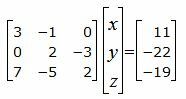 | (21) |
Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
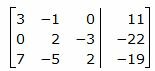 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a1 1. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:
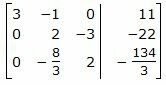 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:
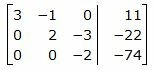 |
Второй этап. Обратный ход Гаусса.
Исключим элементы 3-го столбца матрицы выше элемента a33. Для этого сложим строку 2 со строкой 3, умноженной на −3/2:
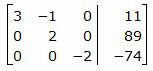 |
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:
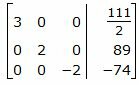 |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
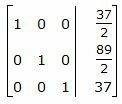 |
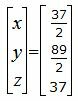 |
Ответ. Точка пересечения прямой L1 и плоскости α имеет следующие координаты:
| M (37/2, 89/2, 37). |
Пример 2. Найти точку пересечения прямой L1:
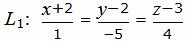 | (22) |
| α: 6x+2y+z+7=0. | (23) |
Представим уравнение (22) в виде двух уравнений:
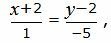 | (24) |
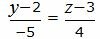 | (25) |
Сделаем перекрестное умножение в уравнениях (24) и (25):
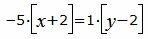 |
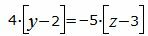 |
Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:
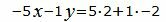 |
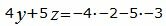 |
Для нахождения точки пересечения прямой L1 и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):
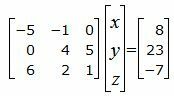 | (28) |
Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:
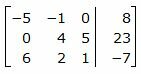 |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:
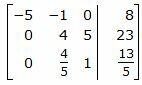 |
Исключим элементы 2-го столбца матрицы ниже элемента a22. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:
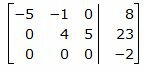 |
Из расширенной матрицы восстановим систему линейных уравнений:
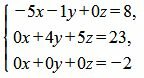 | (29) |
Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство. Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L1 и плоскость α не пересекаются, т.е. они параллельны.
Ответ. Прямая L1 и плоскость α параллельны, т.е. не имеют общую точку.
Пример 3. Найти точку пересечения прямой в параметрическом виде L1:
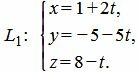 | (30) |
| α: 2x+y−z+11=0. | (31) |
Решение. Для нахождения точки пересечения прямой L1 и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):
| 2(1+2t)+(−5−5t)−(8−t)+11=0. |
| 2+4t−5−5t−8+t+11=0. | (32) |
Упростив уравнение, получим:
Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L1 удовлетворяет уравнению плоскости α. Следовательно прямая L1 лежит на плоскости α.
Ответ. Прямая L1 лежит на плоскости α.
Видео:Построение точки пересечения прямой и плоскости | Стереометрия #29 | ИнфоурокСкачать

Нахождение уравнений прямой, заданной пересечением двух плоскостей
Этот онлайн калькулятор находит уравнения прямой, заданной пересечением двух плоскостей в пространстве.
Этот онлайн калькулятор предназначен для проверки решений задач, которые можно сформулировать следующим образом:
Записать канонические уравнения прямой, заданной уравнениями двух плоскостей
Вы задаете коэффициенты уравнений плоскостей, калькулятор выдает уравнения прямой в канонической форме. Немного теории, как обычно, можно почерпнуть под калькулятором
Нахождение уравнений прямой, заданной пересечением двух плоскостей
Канонические уравнения прямой, заданной пересечением двух плоскостей
Если плоскости пересекаются, то система уравнений, приведенная в начале статьи, задает прямую в пространстве. Для записи уравнений этой прямой в каноническом виде, надо найти какую либо точку, принадлежащую этой прямой, и направляющий вектор.
Точка, принадлежащая прямой, также принадлежит и каждой из плоскостей, то есть является одним из решений системы уравнений выше. Для нахождения точки, принадлежащей прямой, переходят от системы из двух уравнений с тремя неизвестными к системе из двух уравнений с двумя неизвестными, произвольно принимая какую-либо координату точки за ноль. Как правило, при решении задач, выбирают ту координату, при занулении которой решение системы из двух уравнений с двумя неизвестными дает в ответе целые числа. Калькулятор учитывает этот факт и также пытается найти целочисленное решение, зануляя все координаты по очереди.
Направляющий вектор прямой ортогонален нормальным векторам плоскостей, которые задаются коэффициентами A, B и С в общем уравнении плоскости . Таким образом его можно найти как результат векторного произведения нормальных векторов плоскостей .
Точка и вектор дают нам канонические уравнения прямой:
Существуют частные случаи, когда одна или две координаты направляющего вектора равны нулю.
В случае, если нулю равны две координаты, направляющий вектор коллинеарен одной из координатных осей. Соответственно, точки прямой могут принимать любое значение по этой оси, при этом значения по двум другим осям будут постоянны. Например, если двумя нулевыми координатами будут y и z, канонические уравнения прямой будут выглядеть так:
В случае. если нулю равна одна координата, направляющий вектор лежит в одной из координатных плоскостей (плоскостей, образованных парами координатных осей), значение координаты по третьей оси, ортогональной этой плоскости (как раз той, для которой координата направляющего вектора равна нулю), опять будет постоянным. Например, если нулевой координатой будет x, то канонические уравнения прямой будут выглядеть так:
Эти случаи также учитываются калькулятором.
Видео:Найти точку пересечения прямой и плоскостиСкачать

Онлайн калькулятор. Уравнение плоскости
Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.
Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.
Видео:Пересечение прямой и плоскостиСкачать

Найти уравнение плоскости
Выберите метод решения исходя из имеющихся в задаче данных:
В задаче известны:
Ввод данных в калькулятор для составления уравнения плоскости
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления уравнения плоскости
- Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.
Теория. Уравнение плоскости.
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки
В зависимости от условий задачи уравнение плоскости можно составить следующими способами:
- Если заданы координаты трех точек A( x 1, y 1, z 1), B( x 2, y 2, z 2) и C( x 3, y 3, z 3), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле
| x — x 1 | y — y 1 | z — z 1 | = 0 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 | |
| x 3 — x 1 | y 3 — y 1 | z 3 — z 1 |
Если заданы координаты точки A( x 1, y 1, z 1) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
💡 Видео
Пересечение прямой и плоскостиСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

23. Точка пересечения прямой и плоскости / Проекция точки на плоскость / Проекция точки на прямуюСкачать

Построение точки пересечения прямой и плоскостиСкачать

17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Задача 13. Найти точку пересечения прямой и плоскости.Скачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

Видеоурок "Общие уравнения прямой"Скачать

Лекция 2. Основная задача начертательной геометрии. Точка пересечения прямой с плоскостью.Скачать

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать