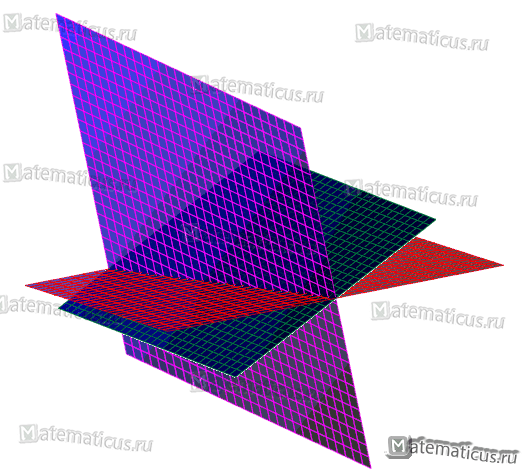
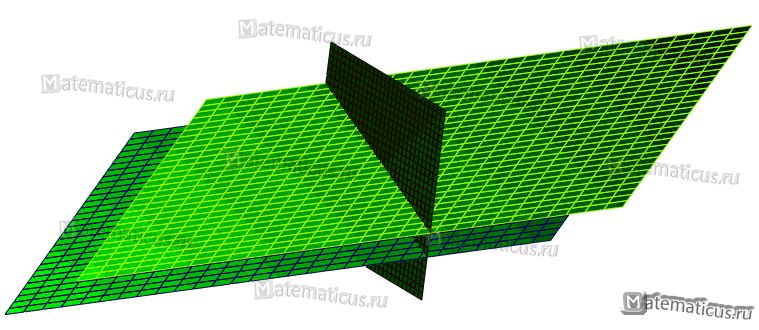
Чтобы найти координаты точки пересечения трех плоскостей, необходимо решить эти уравнения относительно х, у и z, при этом координаты точки пересечения должны удовлетворять уравнениям всех трех плоскостей.
Система уравнений трёх плоскостей имеет вид:
Если определитель этой системы не равен нулю,
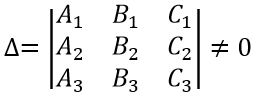
то система имеет единственное решение и тогда три плоскости пересекаются в одной точке.
1. Если три плоскости не имеют ни одной общей точки ( или хотя бы две из них параллельны) — система уравнений не имеет решений.
2.Если плоскости имеют бесчисленное множество общих точек ( все они проходят через одну прямую), то система уравнений имеет бесчисленное множество решений.
3.Если система имеет одну общую точку, то система уравнений имеет только одно решение.
Пример 1
Исследовать, есть ли общие точки у плоскостей
x+y+z=1, x-2y-3z=5, 2x-y-2z=6
Оно имеет бесчисленное множество решений. Значит, три плоскости имеют бесчисленное множество общих точек, т. е. проходят через одну прямую.
Решая эти уравнения совместно, получим координаты искомой точки x=-1; y=1; z=2.
Таким образом плоскости имеют одну общую точку (-1; 1; 2), так как система уравнений имеет единственное решение.
Пример 3
Плоскости
не имеют общих точек, так как плоскости (1) и (2) параллельны.
Система уравнений несовместима (уравнения (1) и (2) противоречат друг другу).
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Линия пересечения плоскостей онлайн
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Видео:Найти точку пересечения 3х плоскостейСкачать

Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
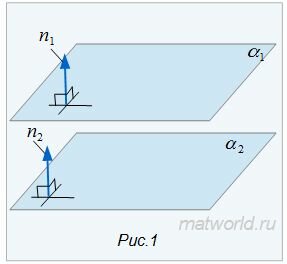
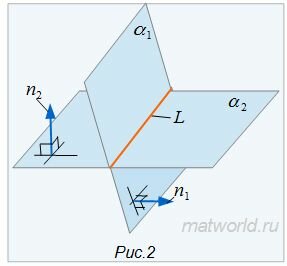
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
 |
Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
 |
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
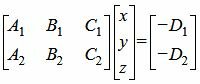 | (4) |
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1=<A1, B1, C1> и n2=<A2, B2, C2> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
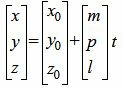 , , | (5) |
Равенство (5) можно записать в следующем виде:
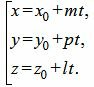 . . | (6) |
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2. Полученное уравнение прямой можно записать в каноническом виде:
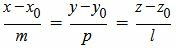 . . |
Пример 1. Найти линию пересечения плоскостей α1 и α2:
| α1: x+2y+z+54=0. | (7) |
| α2: 2x+9y−5z+32=0. | (8) |
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
 . . | (9) |
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
 . . | (10) |
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
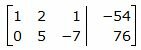 . . |
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
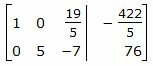 . . |
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
 . . |
 . . | (11) |
где t− произвольное действительное число.
Запишем (11) в следующем виде:
 . . | (12) |
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
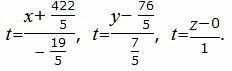 | (13) |
Из равентсв выше получим каноническое уравнение прямой:
 |
Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:
 |
Пример 2. Найти линию пересечения плоскостей α1 и α2:
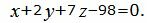 | (14) |
 | (15) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
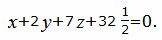 | (16) |
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей α1 и α2:
 | (17) |
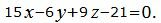 | (18) |
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
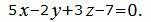 | (19) |
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.
Видео:Найти точку пересечения прямой и плоскостиСкачать

Уравнение пересечения 3 х плоскостей
Перевод Кантора И.А.
Пересечение 3х плоскостей в случае, когда никакие две из них не параллельны — точка. Запишем уравнения плоскостей в виде
Здесь и далее, «.» обозначает скалярное, а «*» — векторное произведение. Точка пересечения
| d1 ( N2 * N3 ) + d2 ( N3 * N1 ) + d3 ( N1 * N2 ) | |
| P = | ————————————————————————- |
| N1 . ( N2 * N3 ) |
Заметим, что знаменатель равен 0, если какие-нибудь 2 плоскости параллельны. Если (N2 * N3) равно нулю, то параллельны вторая и третья. Если такого равенства нет, то (N2 * N3) дает вектор, перпендикулярный и N2 и N3. Скалярное произведение равно нулю тогда и только тогда, когда векторы перпендикулярны. Таким образом, если N1 . (N2 * N3) = 0, то вектор N1 совпадает с N2 или N3 . Значит, плоскости параллельны — точки пересечения не существует.
💥 Видео
4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Линия пересечения плоскостейСкачать

Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

23. Точка пересечения прямой и плоскости / Проекция точки на плоскость / Проекция точки на прямуюСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Точка пересечения трех плоскостейСкачать

Пересечение трех плоскостейСкачать

17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Точка пересечения прямой и плоскостиСкачать

16. Показать что прямые пересекаются и найти точку их пересечения в пространствеСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать