Уравнение перемещения и координаты при рпд

Видео:Перемещение при прямолинейном равномерном движении | Физика 9 класс #4 | ИнфоурокСкачать

Перемещение при равноускоренном движении. Уравнение координаты

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Как, зная тормозной путь, определить начальную скорость автомобиля и как, зная характеристики движения, такие как начальная скорость, ускорение, время, определить перемещение автомобиля? Ответы мы получим после того, как познакомимся с темой сегодняшнего урока: «Перемещение при равноускоренном движении, зависимость координаты от времени при равноускоренном движении».

Видео:Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать

Прямолинейное равномерное движение — формулы, уравнения и примеры

Видео:Уравнение равномерного прямолинейного движения | Физика 10 класс #3 | ИнфоурокСкачать

Общие сведения

Под движением в физике понимают изменение координат тела относительно других объектов с течением времени. Раздел, который изучает происходящее, называется кинематикой. Эта наука исследует только процессы перемещения, не беря во внимание причин его вызвавшего. Часто за тело принимается материальная точка, физическими размерами которой пренебрегают. Это возможно, так как любой объект можно рассматривать как совокупность связанных точек.

Систему, состоящую из неподвижных относительно друг друга тел, можно рассматривать как начало отсчёта при движении. Для этого составляется группа уравнений, которые определяют, как изменяется положение перемещающейся точки с течением времени. Другими словами, определяют координаты тела для любого момента. Называют их уравнениями движения. В декартовых координатах система выглядит так: x = f1 (t); y = f2 (t); z = f3 (t).

Существуют следующие виды движения:

• равномерное прямолинейное;
• равноускоренное;
• перемещение по окружности;
• гармонические колебания.

Все эти изменения положения в пространстве отличаются по виду скорости, ускорения и принципа смены координат. Линия, по которой перемещается материальная точка, называется траекторией движения. По сути, это пройденный телом путь. При криволинейном перемещении, в отличие от прямолинейного, модуль движения всегда будет превышать путь. Это связано с тем, что расстояние, пройденное по дуге всегда будет больше стягивающей хорды.

Рассматривая перемещающиеся тела через одинаковые временные промежутки, можно выделить равномерные и неравномерные движения. Кроме этого, существуют перемещения тела параллельно самому себе — поступательные. Криволинейное движение можно рассматривать как самостоятельный вид изменения положения, а можно свести его к сумме движений по дугам окружностей с различными радиусами кривизны.

При исследовании движения часто измеряют быстроту смены положения, то есть скорость. Если моменту времени соответствует радиус-вектор движущегося тела, то за малый промежуток времени материальная точка переместится на расстояние: Δs = Δr = r2 — r1. Но для характеристики перемещения используют не саму скорость, а её среднее значение: Vср = Δs / Δt.

Видео:Урок 13. Решение задач на РПДСкачать

Принцип исследования перемещения

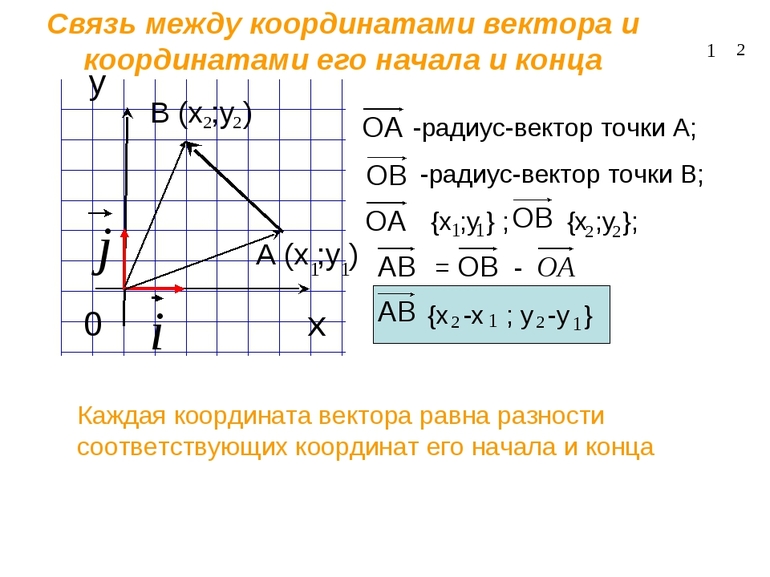
Для того чтобы изучить движение тела в пространстве, нужно выбрать систему отсчёта. Пусть имеется тело, находящееся в точке А. Через некоторое время оно переместилось в точку В. Эти две координаты можно соединить прямым отрезком, являющимся вектором перемещения S. Так как известно, где находилось тело вначале и S, то можно определить его положение в любое время вне зависимости от вида передвижения тела.

В механике работают не с самим вектором, а его проекцией. Поэтому для исследования изменения положения нужно выбрать систему координат. За неё принимаются оси ординаты и абсциссы. Тогда начальное положение можно задать как X0 и Y0, а конечное X, Y. Решение основной задачи механики заключается в возможности указать положение в любой момент времени. То есть найти x (t) и y (t). Для этого понадобится знать X0 и Y0.

Эти значения являются фиксированными и не зависят от времени. Совершённое перемещение можно описать как раз с помощью проекции разности конца положения и начала: X — X0 = Sx; Y — Y0 = Sy. Отсюда можно вывести фундаментальное правило нахождения изменения положения для любой точки времени:

Таким образом, чтобы исследовать прямолинейное равномерное движение, нужно решить систему уравнений, а для этого необходимо знать начальное положение и изменение проекции перемещения тела с течением времени на координатную ось.

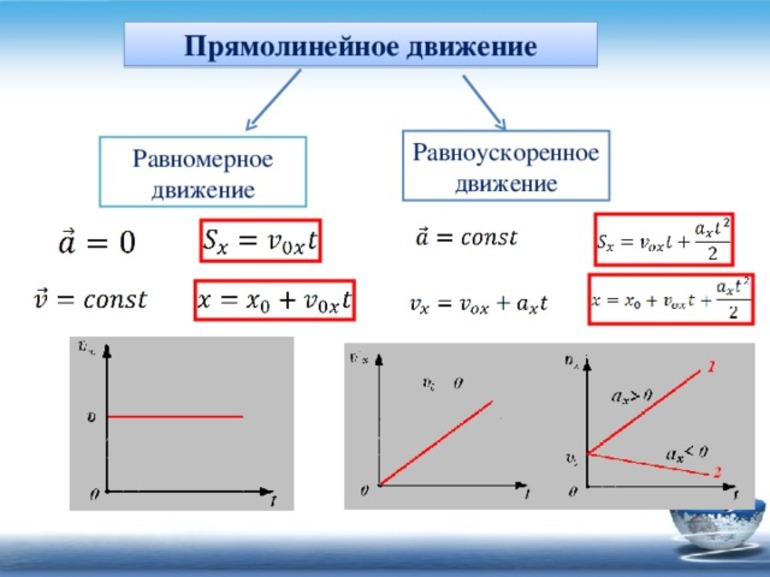
Под равномерным движением понимается перемещение, когда тело за любые промежутки времени проходит равное расстояние. Прямолинейным оно является тогда, когда точка проходит путь по прямой линии. Значит, если за любые равные промежутки времени тело, совершает одинаковое перемещение, то пройденный путь называют РПД (равномерно-прямолинейным). Например, за Δ t равное единице тело преодолеет расстояние равное S1, за Δt2 соответственно S2. Получается, что вектор перемещения материальной точки всегда направлен в одну сторону и имеет один и тот же модуль.

Следует отметить, что характеристикой такого изменения положения является скорость РПД. Для её определения используется отношение вектора перемещения точки к времени, за которое оно произошло: V = S / t, При этом в формуле время может иметь любое значение. Оно является скалярной величиной и неизменным. Значит, скорость РПД можно описать постоянным вектором, сонаправленным с перемещением вектора расстояния.

Видео:9 класс, 3 урок, Графики прямолинейного равномерного движенияСкачать

Нахождение вектора

Чтобы решить главную задачу механики относительно РПД, нужно воспользоваться формулой для нахождения вектора скорости. Из этого определения следует, что S = V * t. Известно, что если имеется соотношение векторов, то его же можно использовать для их проекций на координатные оси. Значит, Sx = Vx * t и Sy = Vy * t. Следовательно, если известны проекции скорости, то можно определить и вектор проекции перемещения в любое время. Отсюда следует, что решение основной задачи для РПД будет иметь вид:

Эти два уравнения всегда нужно рассматривать в совокупности, так как положение тела задаётся на плоскости двумя координатами. Но на самом деле такой системой пользоваться не очень удобно. Поэтому на практике применяют упрощённое выражение.

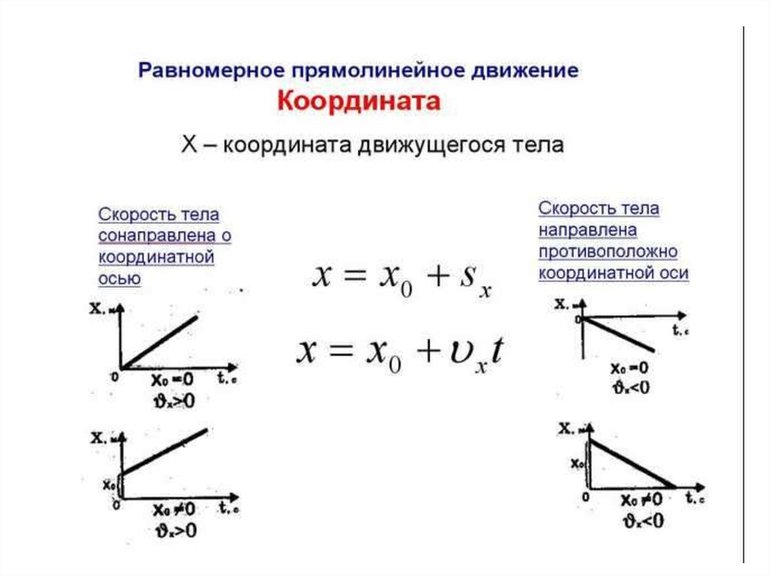
Икс и игрек нулевые зависят от значений координат. Формула изменит вид в зависимости от того, какие выбрать за начальные. Так, выражение значительно упростится, если вектор скорости будет направлен вдоль одной из координатных осей. В результате тело будет лежать на одной из них в начальный момент.

Например, пусть это будет ось икс. Если её расположить так, что она будет размещена параллельно вектору скорости, то ось игрек будет ему перпендикулярна. Смещая координатные оси, точку начального положения можно поместить на ось абсциссы. Для такой повёрнутой системы совокупность уравнений РПД будет также справедливым. Но игрек начальный для рассматриваемой системы будет равняться нулю. Ему же будет равна и проекция скорости на ординату. Учитывая это система главных выражений примет вид:

Фактически получился частный случай общего вида решения основной задачи механики. Так как второе уравнение никакой информации не даёт (тождественный ноль), то его можно убрать. Отсюда следует, что РПД рационально описывать, направляя координатную ось вдоль вектора скорости и выбирать начальное положение точки на координатной прямой.

Тогда получается упрощённый вариант главной формулы: x (t) = x0 + Vx + t. При этом направление вектора скорости значение не имеет. По нему он может как совпадать с осью, так и быть ей противоположным. Нужно отметить, что Vx является проекцией и может быть положительной или отрицательной величиной. В первом случае тело движется вдоль координатной прямой, а во втором в противоположном её направлении.

Видео:Равномерное прямолинейное движение - физика 9Скачать

Решение задач

Физика — это наука, которая позволяет не только знать какие-либо законы и определения, но и учит использовать их на практике. Самостоятельное решение примеров позволяет закрепить имеющиеся знания. Существуют типовые задания, с помощью которых можно проработать изученный материал. Вот некоторые из них:

1. Определить, какие из далее приведённых формул описывают прямолинейное равномерное движение и какие из них не могут быть применимы к перемещению: S = 5 — 2t; V = 5 — 2t. Для того чтобы можно было дать ответ нужно вспомнить формулы, описывающие РПД: x = x0 + Vx * t и Sx = Vx * t. Если рассмотреть второе выражение, то можно утверждать, что x0 = 5, а Vx = -2. Отсюда следует, что оно полностью соответствует условию для РПД. В первом же выражении находится модуль вектора перемещения. Если t = 0 (в начальный момент времени), то S = 5. Такого быть не может, значит, формула не имеет смысла.
2. При движении вдоль оси икс координата точки за первые пять секунд изменилась от десяти метров до минус десять. Найти модуль скорости и проекцию. Для решения за основу берётся главная формула ПРД: x (t) — x0 = Vx * t. Отсюда Vx = (x (t) — x0) / t. Применительно к исходным данным она будет иметь вид: Vx = (x1 — x0) / t = (-10м — 10м) / 5 с = — 4 м / с. Так как тело движется вдоль прямой икс, то модуль скорости будет равняться минус проекции. Значит |V| = 4 м / с. Закон же, описывающий движение, будет следующим: x (t) = 10 — 4 * t.
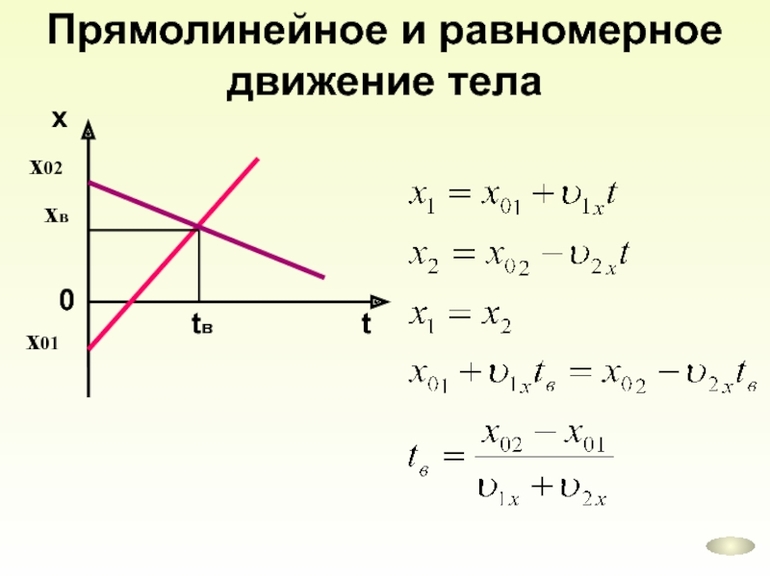
3. Собака бежит за велосипедистом по прямолинейному участку шоссе. Движение человека описывается уравнением x1 = 25 + 10 * t, а животного x2 = -35 + 12 * t. Узнать, догонит ли собака велосипедиста. Можно предположить, что четвероногий друг догонит едущего на велосипеде. Чтобы это подтвердить нужно, определить, когда настанет этот момент. Итак, для того чтобы собака догнала велосипедиста она должна изначально быть сзади него и бежать с большей скоростью. Так как в начальный момент координата человека равна 25, а животного — 35, то собака сзади, при этом 12t > 10t. Условия выполняются, а значит предположение верное. Встреча же их должна произойти в один и тот же момент времени Tвст. Значит, 25 + 10 * Tвст = — 35 + 12 * Tвст → 60 = 2 * Tвст → Tвст = 30 секунд.

Таким образом, решение задач на ПРД требует логического мышления и знания нескольких формул. Кроме этого, можно использовать и графическое описание, то есть изображать график движения тела на координатной плоскости. Для этого в формулу подставляют значения и строят по результатам зависимость.

Видео:Уравнение координат при равноускоренном движенииСкачать

Перемещение и путь при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

• Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
• Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Видео:Урок 12. Равномерное прямолинейное движениеСкачать

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

• Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
• Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

• 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
• 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:

x ( t ) = x 0 + v 0 t + a t 2 2 . .

Теперь мы можем выделить кинематические характеристики движения тела:

Перемещение тела определяется формулой:

s = v 0 t + a t 2 2 . .

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

x ( t ) = v 0 t + a t 2 2 . . = 5 t − 3 t 2

Кинетическая энергия тела определяется формулой:

Скорость при прямолинейном равноускоренном движении равна:

v = v 0 + a t = 5 − 6 t

Поэтому кинетическая энергия тела равна:

E k = m ( 5 − 6 t ) 2 2 . . = 0 , 2 2 . . ( 5 − 6 t ) 2 = 0 , 1 ( 5 − 6 t ) 2

Следовательно, правильная последовательность цифр в ответе будет: 34.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

1. Определить, какому типу движения соответствует график зависимости координаты тела от времени.
2. Определить величины, которые характеризуют такое движение.
3. Определить характер изменения величин, характеризующих это движение.
4. Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Охарактеризовать движение тела на различных участках графика.
2. Выделить участки движения, над которыми нужно работать по условию задачи.
3. Записать исходные данные.
4. Записать формулу определения искомой величины.
5. Произвести вычисления.

Решение

Весь график можно поделить на 3 участка:

1. От t₁ = 0 c до t₂ = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
2. От t₁ = 10 c до t₂ = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
3. От t₁ = 30 c до t₂ = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

1. От t₁ = 20 c до t₂ = 30 с — с равномерным движением.
2. От t₁ = 30 c до t₂ = 50 с — с равнозамедленным движением.

• Для первого участка. Начальный момент времени t₁ = 20 c. Конечный момент времени t₂ = 30 с. Скорость (определяем по графику) — 10 м/с.
• Для второго участка. Начальный момент времени t₁ = 30 c. Конечный момент времени t₂ = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

🎥 Видео

Примеры решения задач по теме: "Равномерно прямолинейное движение"Скачать

Определение координаты движущегося тела | Физика 9 класс #3 | ИнфоурокСкачать

Решение графических задач на равномерное движениеСкачать

Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Физика - уравнения равноускоренного движенияСкачать

Система отсчёта. Определение координаты тела. Равномерное, прямолинейное движениеСкачать

РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Уравнение движенияСкачать

Физика 10 класс (Урок№2 - Равномерное прямолинейное движение материальной точки.)Скачать

Физика - перемещение, скорость и ускорение. Графики движения.Скачать

Прямолинейное движение. 10 класс.Скачать

УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать