3.3 Переходные процессы в цепях второго порядка
Цепи второго порядка содержат два реактивных элемента; это могут быть две индуктивности, две емкости или емкость с индуктивностью. Кроме того, цепь включает некоторое количество резистивных элементов и независимых источников энергии, которые для простоты анализа будем считать стационарными. В зависимости от наличия тех или иных реактивных элементов, решение задачи следует искать или для переменной состояния i L ( t) , или для u C ( t). Форма записи решения определена общей теорией:
где p1 и p2 — корни характеристического уравнения.
Поиск решения выполняется в той же последовательности, что и для цепей первого порядка:
1. Находят корни характеристического уравнения. Они могут быть вещественными разными и отрицательными или вещественными кратными и отрицательными или комплексно-сопряженными с отрицательной вещественной частью;
2. Из анализа цепи после коммутации определяют принужденную составляющую режима 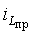
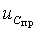
3. Исследуя основные и неосновные начальные условия, находят постоянные интегрирования 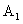
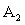
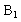
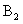
Рассмотрим подробнее каждый шаг решения.
1. Определение корней характеристического уравнения.
Характеристическое уравнение может быть получено классическим методом путем составления системы уравнений по законам Кирхгофа с последующим сведением этой системы к одному дифференциальному уравнению второго порядка. Этот способ подробно описан в учебной литературе и здесь не рассматривается. Как показывают примеры, рассмотренные ранее, этот путь сопровождается достаточно громоздкими преобразованиями.
Было замечено, что характеристическое уравнение содержится внутри
функции входного сопротивления как некоторый инвариант, присущий данной цепи. Рассмотрим этот способ получения характеристического уравнения путем исследования входного сопротивления на примере цепи, представленной на рис.3.13а. Будем считать, что цепь питается от источника постоянного тока и содержит два резистивных сопротивления, индуктивность и емкость. После коммутации ( t>0) (ключ S замыкается) переходный процесс в цепи, изображенной на рис.3.13б, развивается за счет независимого источника тока, а также за счет энергии, запасенной в реактивных элементах цепи. Свободная составляющая режима, определяемая корнями характеристического уравнения, не зависит от внешнего источника питания, а определяется только параметрами элементов ветвей и способом их соединения. Точно так же не зависит от внешних источников питания и функция входного сопротивления [1]. Поэтому возникает идея поискать корни характеристического уравнения внутри функции входного сопротивления.
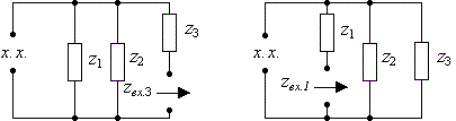
На рис.3.13в и рис.3.13г представлены комплексные схемы замещения цепи, которые следует составить для определения входного сопротивления со стороны
первой и третьей ветви, где 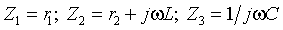
Рис. 3.13. Схема RLC -цепи второго порядка:
а) исходная цепь
б) схема после коммутации
в) входное сопротивление со стороны третьей ветви
г) входное сопротивление со стороны первой ветви
Объединяя параллельно и последовательно соединенные ветви, найдем входные сопротивления со стороны обозначенных зажимов
Числители полученных выражений совпадают, а знаменатели различны. Аналогичный результат получим, если найдем входное сопротивление со стороны второй ветви. Следовательно, числитель входного сопротивления со стороны любой ветви является некоторым расчетным инвариантом, определяемым топологией цепи. Числитель этого инварианта при замене комплексной переменной jω на p совпадает с характеристическим полиномом. Используя эту замену и, приравнивая числитель к нулю, получим характеристическое уравнение:
После замены в числителе переменной jω на p и деления на коэффициент при старшем члене получим уравнение второй степенин.Найдем корни этого уравнения
На основании этого анализа сформулируем порядок получения характеристического уравнения цепи:
а. Для времени t>0 следует изобразить комплексную расчетную цепь;
б. Исключить из схемы все независимые источники энергии: источники тока разомкнуть, источники напряжения замкнуть накоротко. Найти входное сопротивление со стороны любой ветви и записать это выражение в виде дробно-рациональной функции, где в числителе и в знаменателе образуются полиномы по степеням jω
в. Числитель полученного выражения, совпадающий с характеристи-ческим полиномом, приравнять к нулю, предварительно заменив переменную jω на p. Найти корни характеристического уравнения и записать решение для искомой переменной состояния в виде (3.17) или (3.18).
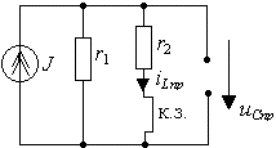
Рис. 3.14. Схема для определения принужденных составляющих режима
2. Определение принужденной составляющей режима при стационарном воздействии находят для момента времени t = ∞, когда переходный процесс в цепи уже закончен. Для рассматриваемого в примере режима постоянного тока исследуемая схема приведена на рис.3.14, где индуктивность заменена короткозамкнутой перемычкой, а емкость разрывом. Используя правило деления тока на части, найдем
3. Постоянные интегрирования A1 и A2 (или B1 и B2) можно найти на основании основных и неосновных начальных условий. Основные начальные условия определяются законами коммутации по схеме докоммутационного состояния цепи. Для рассматриваемого примера такая схема приведена на рис.3.15а, из анализа которой следует
что дает одно уравнение для определения постоянных интегрирования:
Видео:Расчет переходного процесса в цепи второго порядка.Скачать

Переходной процесс в цепи второго порядка
5 ПЕРЕХОДНОЙ ПРОЦЕСС В ЦЕПИ ВТОРОГО ПОРЯДКА
Рисунок 5.1 — Схема цепи
Уравнение цепи имеет вид

Дифференцируя обе части выражения (5.1), получим уравнение второго порядка для тока i в цепи:

Однородное уравнение, определяющее свободный ток, можно записать

Введем обозначения 





Ток переходного режима

Ток установившегося режима 

Произвольные постоянные интегрирования A1 и A2 определяют из начальных физических условий: 
Для определения постоянных A1 и A2 надо знать значение тока и всех его производных до (n – 1) включительно в начальный момент времени. В данном случае необходимо знать начальное значение тока и его первой производной. Начальное значение первой производной тока находится из уравнения цепи (5.1) при (t = 0)

где u(0) – значение приложенного напряжения u(t) при t = 0.
Из последнего уравнения получаем

Из уравнения (5.8) для производной тока имеем

Уравнения для нахождения постоянных интегрирования

где 
В качестве примера рассмотрим расчет переходного процесса классическим методом для схемы, изображенной на рис. 5.2. Определить ток
Рисунок 5.2 — Расчетная схема
1. Для цепи после коммутации составляются уравнения по I и II законам Кирхгофа.
2. Определяются независимые начальные условия 


3. Искомая величина записывается в виде

4. Установившуюся составляющую определяют из расчета режима цепи после коммутации 
5. Составляется характеристическое уравнение, и определяются его корни

Корни могут быть:
действительные разные p1 и p2; действительные равные p1 = p2 = p; комплексно сопряженные 
где б – коэффициент затухания;
щсв – угловая частота свободных колебаний.
6. В соответствии с полученными корнями характеристического уравнения записывается свободная составляющая:
1) 
2) 
3) 

7. Искомое решение для первого случая

8. Определяются постоянные интегрирования A1 и A2:


Уравнения п.1 для момента времени t = 0 запишутся как

Независимые начальные условия i(0) и 

Для определения 
9. После определения постоянных интегрирования A1 и A2 подставляют их в искомое решение и расчет окончен.
Для определения других токов и напряжений не требуется выполнять все этапы расчета. Можно использовать известные выражения

В этом случае приложенное напряжение, а также ток установившегося режима равны нулю:

Для определения произвольных постоянных интегрирования в уравнении необходимо положить: 
Рисунок 5.3 — Расчетная схема
Обозначим 


Напряжения на катушке и конденсаторе

При выводе последнего уравнения учитывалось, что 
5.1 Корни характеристического уравнения
Характер процессов при разряде конденсатора оказывается различным в зависимости от того, будут ли корни характеристического уравнения вещественными или комплексными, что определяется соотношениями между параметрами R, L и C.
Рассмотрим возможные случаи.
1. Пусть корни характеристического уравнения вещественны и отличны друг от друга. Это имеет место при условии

Так как 





Ток i не меняет своего направления, т. е. конденсатор все время разряжается. Такой односторонний разряд конденсатора называют апериодическим. Кривые изменения напряжений показаны на рис. 5.5.
Видео:Семинар №9 "Приведение уравнения второго порядка к каноническому виду"Скачать

Уравнение переходного процесса второго порядка
При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.
При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.
Основные методы анализа переходных процессов в линейных цепях:
- Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
- Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
- Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
- Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.
- Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).
Классический метод расчета
Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.
В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в табл. 1.
Таблица 1. Связь мгновенных значений напряжений и токов на элементах электрической цепи
| Резистор (идеальное активное сопротивление) | |||||||
| Катушка индуктивности (идеальная индуктивность) | |||||||
| Конденсатор (идеальная емкость) | |||||||
 . . | (1) |
Подставив в (1) значение тока через конденсатор

получим линейное дифференциальное уравнение второго порядка относительно

В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии, имеет вид:
 , , | (2) |
где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); 

Порядок данного уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.
В общем случае порядок дифференциального уравнения определяется соотношением
 , , | (3) |
где 



Наличие индуктивных связей на порядок дифференциального уравнения не влияет.
Как известно из математики, общее решение уравнения (2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (2), применительно к электротехнике в качестве последнего удобно принять решение 

Частное решение 

Вторая составляющая 

В соответствии с вышесказанным, общее решение уравнения (2) имеет вид
 | (4) |
Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса.
Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении искомой переменной х, справедлив только для линейных цепей.
Начальные условия. Законы коммутации
В соответствии с определением свободной составляющей 


Таблица 2. Законы коммутации
Первый закон коммутации (закон сохранения потокосцепления)
Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: 
Второй закон коммутации (закон сохранения заряда)
Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: 
Доказать законы коммутации можно от противного: если допустить обратное, то получаются бесконечно большие значения 

На практике, за исключением особых случаев (некорректные коммутации), допустимо использование указанных законов в другой формулировке, а именно:
первый закон коммутации – в ветви с катушкой индуктивности ток в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: 
второй закон коммутации – напряжение на конденсаторе в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: 
Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис. 2, переходные процессы в которых относятся к так называемым некорректным коммутациям (название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).
Действительно, при переводе в схеме на рис. 2,а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа 

Зависимыми начальными условиями называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для 

Пример. Определить токи и производные 

В соответствии с законами коммутации


На основании второго закона Кирхгофа для момента коммутации имеет место

и 
Для известных значений 

определяется 
Значение производной от напряжения на конденсаторе в момент коммутации (см. табл. 1)

Корни характеристического уравнения. Постоянная времени
Выражение свободной составляющей 
Таблица 3. Выражения свободных составляющих общего решения
Вид корней характеристического уравнения
Выражение свободной составляющей
Корни 
Корни 
Пары комплексно-сопряженных корней
Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.
При вещественных корнях 
Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением

которое называется декрементом колебания, или натуральным логарифмом этого отношения

называемым логарифмическим декрементом колебания, где 
Важной характеристикой при исследовании переходных процессов является постоянная времени t , определяемая для цепей первого порядка, как:

где р – корень характеристического уравнения.
Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
📹 Видео
Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Расчет переходного процесса в цепи второго порядка. Комплексные корниСкачать

ПП в цепях 2 порядка вступлениеСкачать

Классический метод расчета переходных процессов в цепях второго порядка Calculation of ElectricalСкачать

Лекция 122. Переходные процессыСкачать

Расчет переходного процесса RLC цепи Классическим методомСкачать

Переходные процессы в цепи с емкостью. Второй закон коммутацииСкачать

Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Классический метод расчета электрической цепи. Пример 2Скачать

Расчет переходных процессов классическим методомСкачать

Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

Лекция 091-5. Расчет переходных процессов классическим методом. Корни характеристического уравненияСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Переходные процессы. Анализ разветвленной цепи 2 порядка. Часть 1Скачать

Пример 6 | Классический метод расчета цепи первого порядка с конденсаторомСкачать

Основы электротехники. 06. Переходные процессыСкачать

ТОЭ79 Переходные процессы. Второй способ создания характеристического уравнения электрической цепи.Скачать

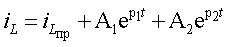
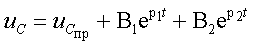
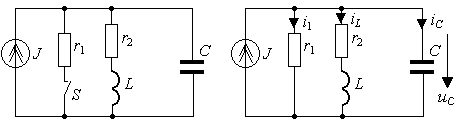
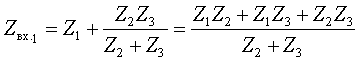
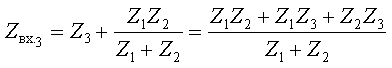
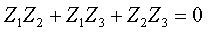
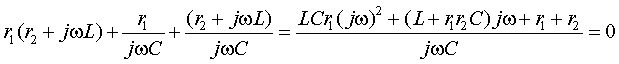
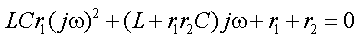
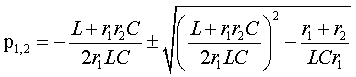
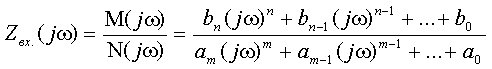
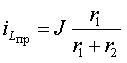
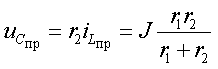
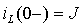
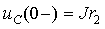














 ;
; ,
,
 ;
;












