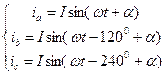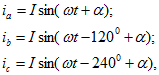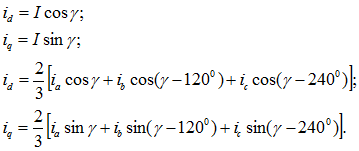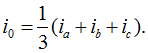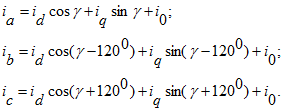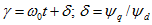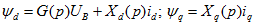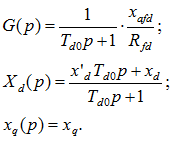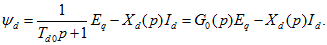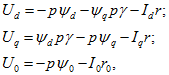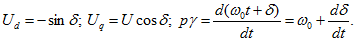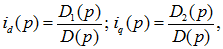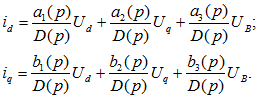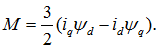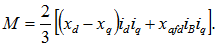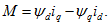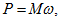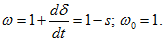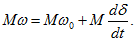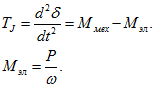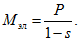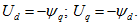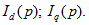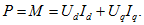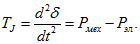Уравнения Парка — Горева связывают между собой мгновенные значения токов, магнитных потоков, напряжений в осях координат (d, q), связанных с ротором.
Мгновенные значения параметров режима определяют как проекции на оси времени фаз а, b, с вектора тока (напряжения, ЭДС, потокосцепления), вращающегося с угловой скоростью 
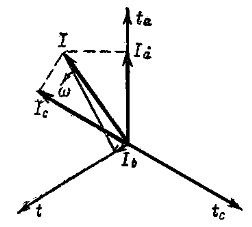
Оси времени ta, tb, tc фаз a, b, с неподвижны и совпадают с осями обмоток статора (рис. 2.1). Мгновенные значения фазных токов равны:
где 
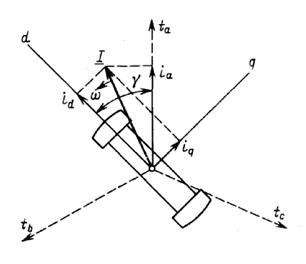
Рис.2.1 Обобщенный вектор тока 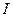
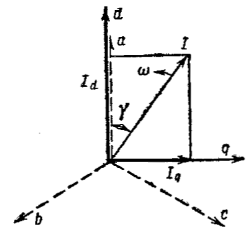
Проекции обобщенного вектора тока на оси d, q, связанные с ротором, дают значения продольного и поперечного токов (рис. 2.2):
При наличии токов нулевой последовательности
Соотношения, аналогичные приведенным выше, справедливы для напряжений, ЭДС и потокосцеплений.
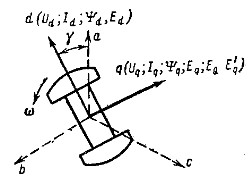
Рис. 2.2. Обобщенный вектор тока I и проекции его
на продольную и поперечную оси ротора
Связь между мгновенными значениями фазных величин и величин в продольной и поперечной осях устанавливается на основе уравнений:
Угол 
где 
В случаях симметричного режима энергосистемы токи нулевой последовательности отсутствуют ( 
Значения потокосцепления статора в поперечной и продольных осях определяются из выражений:
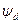


где G(p)—операторная проводимость машины;
Xd(p), Xq(p) — операторные сопротивления машины в продольной и поперечной осях;
Uf — напряжение возбуждения машины.
Для машины без демпферных обмоток и эквивалентных им контуров:



Если известна ЭДС 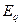

где 



Для машины с демпферными обмотками значения потокосцепления статора в поперечной и продольных осях 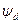

Рис.2.3 Основные параметры синхронной машины для принятых направлений осей.
Уравнения Парка – Горева для принятых на рис.2.3. направлениях осей примут вид:



где 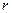




В системе относительных единиц 

Третье уравнение системы относится к случаю несимметричного режима или несимметричной схемы.
Уравнения, приведенные выше, полностью описывают переходный процесс машины, работающей на шины неизменного напряжения. Для анализа переходного процесса в сложной энергосистеме уравнения составляются для каждого элемента (генераторов, нагрузок, участков сети) и решаются совместно.
Решение системы уравнений Парка – Горева относительно токов или других величин, рассматриваемых как неизвестные, проводится в операторной форме (для изображений), например находятся значения токов


где 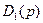
Характер переходного процесса в системе определяется знаком действительной части корней определителя D(р). При Re(pt, . . рn)
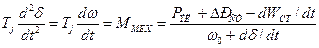
где 
Для определения параметров при переходных процессах можно использовать упрощенные уравнения Парка – Горева. Для получения этих уравнений отказываются от учета влияния:
1) апериодической составляющей тока статора (трансформаторной ЭДС);
2) периодических токов ротора, связанных с апериодическими составляющими тока статора;
3) активного сопротивления в цепи статора.
В системе относительных единиц при 

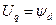
Данные уравнения положены в основу расчетов периодической составляющей токов короткого замыкания при обычно принимаемых допущениях.
При принятых предпосылках отдаваемая мощность численно равна вращающемуся моменту; поэтому для симметричного режима или режима, условно приведённого к симметричному,

Уравнение относительного движения ротора
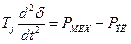
На основе этих расчетных уравнений (их иногда называют уравнениями Лонглея или уравнениями Лебедева — Жданова) обычно ведутся проектные и эксплуатационные расчеты устойчивости. Они позволяют для расчетов переходных процессов пользоваться соотношениями, вытекающими из векторной диаграммы установившегося режима [рис.2.1].
- Система относительных единиц. Система уравнений явнополюсной синхронной машины в системе относительных единиц Горева
- Система относительных единиц. Система уравнений явнополюсной синхронной машины в системе относительных единиц Горева
- Математическое описание переходных процессов
- Дополнительно по теме
- 🎥 Видео
Видео:Моделирование СМ Часть 4 Установившийся режим синхронной машиныСкачать

Система относительных единиц. Система уравнений явнополюсной синхронной машины в системе относительных единиц Горева
Видео:Преобразование Парка - ГореваСкачать

Система относительных единиц. Система уравнений явнополюсной синхронной машины в системе относительных единиц Горева
Система относительных единиц
Система уравнений синхронной машины обычно записывается в относительных единицах, вследствие чего упрощается запись данных уравнений и облегчается сравнение результатов исследования переходных процессов для машин различной мощности.
Система относительных единиц — способ расчета параметров в системах передачи электроэнергии, при котором значения системных величин (напряжений, токов, сопротивлений, мощностей и т.п.) выражаются как множители определенной базовой величины, принятой за единицу.
Существует несколько видов систем относительных единиц, основные из которых: система относительных единиц Горева и система относительных единиц « X ad ». В рамках данной публикации будем рассматривать систему относительных единиц Горева.
Базисные величины статорной цепи
В качестве независимых базисных величин для статорной цепи обычно принимается амплитуда номинальных тока и фазного напряжения, синхронная угловая частота 
Базисные значения тока и напряжения статора (контуров якоря) машины равны амплитуде фазного тока и фазного напряжения:

Базисное значение мощности статорной цепи будет определяться в следующем виде:
Базисное значение угловой скорости равно синхронной угловой скорости при номинальной частоте:

Прочие базисные параметры определяются по следующим соотношениям:


Базисные величины роторной цепи
В качестве независимых базисных величин для роторной цепи принимается такие значения тока, напряжения и потокосцепления роторного контура, которые обусловливают на статоре идеализированной синхронной машины в режиме холостого хода номинальное напряжение.
При протекании базисного тока по роторному контуру (обмотка ротора или демпферные обмотки) в режиме холостого хода при синхронной угловой скорости напряжение статора равно номинальному. Данное утверждение записывается в следующем виде:



Базисные напряжения роторных контуров определяются как произведение базисного тока на активное сопротивление контуров:



Базисные значения сопротивлений роторных контуров принимаются равными активным сопротивлениям контуров:



Представленный подход позволяет легко связать базисные величины статорной цепи базисными величинами роторной цепи.
Определение величины базисного тока ротора и демпферных обмоток.
Базисное значение тока обмотки возбуждения определяется по спрямленной в начале координат характеристике холостого хода машины (см. рис.1), построенной в относительных единицах.
Рис.1. Определение базисного значения тока роторных контуров.
Ток возбуждения отнесен к номинальному току возбуждения на холостом ходе:
где 
Графическое определение базисного тока 




Базисные значения токов демпферных контуров в осях d и q равны:
Преобразим систему уравнений явнополюсной синхронной машины в систему относительных единиц Горева.
Система уравнений для напряжений статорной цепи
Рассмотрим систему уравнений, которая записана для статорной цепи.
Перепишем данную систему уравнений относительно базисных переменных, для этого разделим представленные уравнения на базисное значение напряжения:

Первое уравнение рассматриваемой системы преобразуется к следующему виду:
Второе уравнение рассматриваемой системы преобразуется к следующему виду:
где s — скольжение ротора относительно синхронной оси.
Скольжение — Относительная разность скоростей поля статора и ротора называется скольжением
Скольжение не может быть равным нулю, так как при одинаковых скоростях поля и ротора прекратилось бы наведение токов в роторе и, следовательно, отсутствовал бы электромагнитный вращающий момент.
Скольжение асинхронного генератора 
Система уравнений для потокосцеплений статорных контуров
Рассмотрим систему уравнений, которая записана для потокосцеплений статорных контуров.
Для выполнения дальнейших преобразований системы уравнений введем новые переменные:
› синхронная ЭДС статора 
› синхронная ЭДС, связанные с токами демпферных контуров 
› синхронная ЭДС, связанные с токами демпферных контуров 
C учетом новых введенных переменных система уравнений перепишется в следующем виде:
Перепишем систему уравнений относительно базисных переменных, для этого разделим данные уравнения на базисный поток статорной цепи:
Первое уравнение рассматриваемой системы преобразуется к следующему виду:
Второе уравнение рассматриваемой системы преобразуется к следующему виду:
где синхронное индуктивное сопротивление машины по продольной оси 
синхронное индуктивное сопротивление машины по поперечной оси 
Система уравнений для потокосцеплений роторных контуров
Рассмотрим систему уравнений, которая записана для потокосцеплений роторных контуров.
Умножим данную систему уравнений на выражение 


› переходная ЭДС статора 
› переходная ЭДС, связанная с токами демпферных контуров 
› переходная ЭДС, связанная с токами демпферных контуров 
В результате преобразования получим следующую систему уравнений для потокосцеплений роторных контуров.
Перепишем данную систему уравнений через сопротивления 




Перепишем систему уравнений относительно базисных переменных, для этого разделим данные уравнения на базисное напряжение статорной цепи:
В результате данного преобразования получим следующую систему уравнений (в относительных единицах):
Система уравнений для напряжений роторной цепи
Рассмотрим систему уравнений, которая записана для роторных цепей.
Умножим данную систему уравнений на выражение 


Первое уравнение рассматриваемой системы преобразуется к следующему виду:
Второе уравнение рассматриваемой системы преобразуется к следующему виду:
Третье уравнение рассматриваемой системы преобразуется к следующему виду:
Постоянные времени используемые в уравнениях определяются следующим образом:
› Постоянная времени контура возбуждения 
› Постоянные времени демпферных контуров 
Перепишем полученную систему уравнений относительно базисных переменных, для этого разделим данные уравнения на базисное напряжение:
Первое уравнение рассматриваемой системы преобразуется к следующему виду:
где 
Второе уравнение рассматриваемой системы преобразуется к следующему виду:
Третье уравнение рассматриваемой системы преобразуется к следующему виду:
Система уравнений явнолюполюсной синхронной машины в относительных единицах Горева
В результате преобразования была получена система уравнений явнолюполюсной синхронной машины для вращающейся системы координат (odq) с учетом демпферных контуров, которая представлена в относительных единицах Горева.
1. Система уравнений для напряжений статорной цепи:
2. Система уравнений для потокосцеплений статорных контуров:
3. Система уравнений для потокосцеплений роторных контуров:
4. Система уравнений для напряжений роторной цепи и демпферных контуров (уравнения равновесия напряжений роторных контуров):
В систему уравнений, которая записана в относительных единицах Горева, входят переменные статорной цепи и переменные обмотки ротора:
› Переменные статорной цепи
Переменные 







Переменные 



› Переменные обмотки ротора
Переменные 
Переменные 


Сопротивления, которые входят в систему уравнений синхронной машины
Ниже представлены сопротивления, которые входят в представленную систему уравнений синхронной машины (в именованных единицах).








Примечание:
Для перевода данных переменных сопротивления к базисным единицам достаточно разделить переменные на базисную величину 
Соотношения между переменными 



Вспомогательные ЭДС, которые входят в систему уравнений синхронной машины
Ниже представлены вспомогательные ЭДС, которые входят в представленную систему уравнений синхронной машины (в именованных единицах).






Примечание:
Для перевода переменных из именованных единиц к базисным единицам достаточно разделить переменные на базисную величину напряжения:

Таким образом, вспомогательные ЭДС в относительных единицах Горева определяются следующим образом:
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
Видео:Моделирование СМ. Часть 3. Вывод уравнений Парка-ГореваСкачать

Математическое описание переходных процессов
Дополнительно по теме
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ СИСТЕМАХ
При классификации переходных процессов, различают волновые процессы, электромагнитные и электромеханические. Здесь рассмотрены два последних вида переходных процессов.
Из общих уравнений Парка — Горева, изложенных ниже, могут быть найдены значения токов при любых переходных процессах в системах, в том числе при коротких замыканиях, однако в этом разделе не приводятся расчетные выражения для определения этих токов.
Расчеты по уравнениям Парка — Горева (П.-Г.) довольно сложны и проводятся только при применении вычислительных машин. Обычно при аналитических расчетах, расчетах с помощью статических моделей (расчетных столов) и значительной части расчетов, выполняемых на вычислительных машинах, целесообразно пользоваться упрощенными уравнениями. Правильный выбор системы уравнений и необходимой точности анализа, соответствующей реальной технической задаче, составляет искусство инженера.
Дифференциальные уравнения синхронных машин дают возможность проводить анализ переходных процессов в электрических системах с учетом наибольшего количества влияющих факторов (изменений угловой скорости ротора, апериодических составляющих токов статора, периодических токов ротора, активного сопротивления в цепи статора генератора). Опустив те или иные члены в уравнениях П. — Г., можно получить упрощенные уравнения, применяющиеся: а) для расчетов токов коротких замыканий (без учета изменений скорости); б) для расчета электромеханических переходных процессов, обычно без учета апериодических составляющих тока, статора и периодических тока ротора.
Уравнения П. — Г. связывают мгновенные значения токов, магнитных потоков, напряжений в осях координат (d, q), жестко связанных с ротором.
Мгновенные значения параметров режима — фазные и в осях d, q
Эти значения определяют как проекции на оси времени фаз а, b, с вектора тока, вращающегося со скоростью w. Этот вектор тока (напряжения, э. д. с, потокосцепления) называют обобщенным.
Оси времени 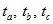
где a — произвольный угол.
Проекции обобщенного вектора тока на оси d и q, жестко связанные с ротором, дают значения, продольного и поперечного токов (рис. 37-2):
При наличии токов нулевой последовательности в системе имеет место соотношение
Соотношения, аналогичные приведенным выше, справедливы для напряжений, э. д. с. и потокосцеплений.
Соотношения между мгновенными значениями фазных величин и величинами в продольной и поперечной осях имеют вид:
Угол g меняется во времени:
где 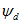
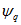
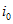
В случае симметричного режима системы токи нулевой последовательности отсутствуют 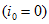
Значения 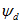
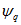
где G(p)-операторная проводимость машины; Xd(p)-операторное сопротивление машины в продольной оси; Xq(p)-то же в поперечной оси; Uв — напряжения возбуждения машины.
Для машины без успокоительных обмоток и эквивалентных им контуров
Если известна э. д. с. Eq, по 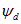
Для машины с успокоительными обмотками в продольной и поперечной осях 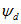
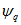
Рис. 37-2. Положение обобщенного вектора тока I в пространстве и его проекции на продольную и поперечную оси ротора.
Уравнения Парка — Горева для синхронной машины в операторной форме
Эти уравнения при принятых на рис. 37-3 направлениях осей имеют вид:
В системе относительных единиц 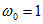
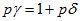
Третье уравнение системы относится к случаю несимметричного режима или несимметричной схемы.
Уравнения, приведенные выше, полностью описывают переходный процесс машины, работающей на шины неизменного напряжения. Для анализа переходного процесса в сложной системе уравнения составляются для каждого элемента (генераторов, нагрузок, участков сети) и решаются совместно.
Решение уравнений, описывающих переходный процесс в системе
Решение приведенной выше системы уравнений относительно токов или других величин, рассматриваемых как неизвестные, проводится в операторной форме (для изображений). Например, находятся значения токов в виде:
где D1(p), D2(p)-частные определители системы; D(p)-общий определитель системы.
Характер переходного процесса в системе определяется знаком вещественной части корней определителя D(p). При 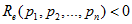
Если изменения напряжений 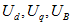
Токи как функции времени находят, переходя от изображения к оригиналам, что может быть сделано с помощью формулы разложения.
Уравнения для вращающего момента и мощности во время относительного движения ротора
При принятых направлениях осей (рис. 37-3) момент электромагнитных сил, действующих на ротор, в общем случае имеет вид
При подстановке 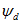
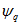
В системе относительных единиц, где коэффициент 3/2 учтен соответствующим выбором базисных величин,
Связь между мощностью, отдаваемой в сеть, и моментом следующая:
где 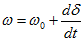
Электромагнитная мощность генератора, передаваемая с ротора на статор,
Уравнение относительного движения ротора в общем виде:
В относительных единицах
Упрощенные уравнения Парка — Горева для определения параметров режима при переходных электромеханических процессах
Эти уравнения применяются при расчетах токов коротких замыканий, устойчивости и т. д. При этом отказываются от учета влияния:
1) апериодической составляющей тока статора (трансформаторной э. д. с);
2) периодических токов ротора, связанных с апериодическими составляющими тока статора;
3) активного сопротивления в цепи статора.
Тогда в системе относительных единиц при 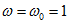
В соответствии с этим упрощаются выражения для токов:
Выражения мощности и электромагнитного момента в этих условиях будут совпадать, так как при принятых предпосылках отдаваемая мощность численно равна вращающему моменту. Для симметричного или условно приведенного к симметричному режима (метод симметричных составляющих) получим:
Здесь 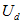
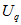
Уравнение относительного движения ротора при принятых допущениях имеет вид
На основе упрощенного выражения момента можно перейти к ряду частных его выражений.
🎥 Видео
Моделирование СМ. Часть 2. Физическая модель синхронной машиныСкачать

Моделирование СМ. Часть 1. Теоретическая справкаСкачать

ЭлМехПП Переподготовка 2 Математическое описание синхронных машинСкачать

Синхронные двигатели, устройство и принцип работыСкачать

Принцип работы синхронного электродвигателяСкачать

Двигатель Tesla Модель 3 - Блестящее конструкторское решениеСкачать

Реактивный двигатель Tesla Model 3 | Принцип работы, почему он ЛУЧШИЙ сегодня?Скачать

Электромеханические переходные процессы. Устойчивость. Уравнение движение ротора.Скачать
Синхронные машиныСкачать

Мгновенный центр вращенияСкачать

Уравнения напряжений обобщенного преобразователяСкачать

Асинхронные и Синхронные двигатели и генераторы. Мощный #энерголикбез ПЕРСПЕКТИВЫ ЭЛЕКТРОДВИГАТЕЛЕЙСкачать

Синхронные машиныСкачать

Синхронный и асинхронный двигатели. Отличия двигателейСкачать

Синхронные машины (часть 2)Скачать