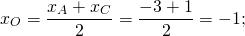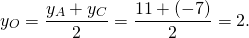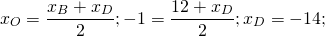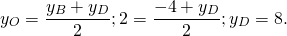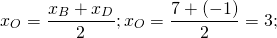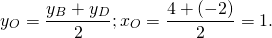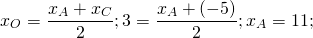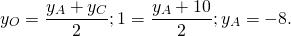Уравнение параллелограмма на координатной плоскости имеет вид

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Уравнение многоугольника

Составление и решение уравнений многоугольников

Видео:Уравнения стороны треугольника и медианыСкачать

Скачать:

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Предварительный просмотр:

Автор работы: Шпакова Маргарита Андреевна, г.о. Тольятти, МБУ СОШ

Научный руководитель: Владимирова Ольга Ивановна, учитель математики первой категории МБУ СОШ № 58.

В школьном курсе математики учащиеся часто встречаются с алгебраическими уравнениями, уравнениями прямых, уравнениями окружностей, квадратными уравнениями и т.д. Что собой представляют уравнения многоугольников, учащиеся не знают.

Как, например, выглядит уравнение треугольника? Можно ли по фигуре на плоскости составить уравнение? Можно ли рассчитать площадь фигуры по заданному уравнению? Можно ли по заданному уравнению определить, что за многоугольник? Решение этих вопросов меня и заинтересовало. В них есть проблема моей исследовательской работы.

Цель работы: изучить и исследовать на примерах методы, которые дают возможность получить уравнение с модулем любого выпуклого многоугольника на плоскости, координаты вершин которого известны. Найти взаимосвязь площади фигуры от ее уравнения.

Основные ЗАДАЧИ исследования:

1. Познакомиться с некоторыми видами уравнений прямых на плоскости (уравнение прямой в отрезках, уравнение прямой, проходящей через две различные точки на плоскости);
2. Научиться составлять уравнение прямой через заданную точку и параллельную другой прямой;
3. Научиться составлять уравнение прямой, проходящей через две заданные точки;
4. Научиться по уравнению строить многоугольник на плоскости и наоборот, по чертежу составлять уравнение многоугольника;
5. Изучить метод областей при решении уравнений, содержащих знак модуля.

Как известно из курса геометрии, любая прямая на координатной плоскости может быть задана уравнением вида

Подобное уравнение называют линейным. Уравнение такого вида называют также общим уравнением прямой на плоскости.

Если ax+by+c = 0 — уравнение некоторой прямой m, то уравнение ax+by+c = p, где р ≠ 0, задает прямую m`, параллельную m. Это следует из того, что данные два уравнения не имеют общих решений, а значит, прямые не имеют общих точек.

У параллельных прямых

Пример1 . Составим уравнение прямой, проходящей через точку М (1;-2) и параллельной прямой 3x-4y+5=0

Подставляя координаты точки М в левую часть уравнения, получаем значение 16. Значит, искомым уравнением прямой будет 3x+4y+5=16 или окончательно 3x+4y-11=0.

Пусть известны координаты двух точек М 1 (x 1 ;y 2 ), М 2 (x 2 ;y 2 ), лежащих на данной прямой. Составим уравнение прямой, проходящей через две заданные точки:

(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0

Пример 2 . Составим уравнение прямой, проходящей через точку М 1 (3;1) и М 2 (2;2).

Получаем такое уравнение (x-3)(2-1)-(y-1)(2-3)=0

после преобразований выходит х+у-4=0.

Если известны координаты (а;0) и (0;b) точек пересечения прямой с осями Ох и Оу, то для этой прямой проще всего записать уравнение в отрезках + = 1.

Рассмотрим на координатной плоскости ху треугольник с вершинами в точках А (х 1 ;у 1 ), В (х 2 ;у 2 ), С (х 3 ;у 3 ). Уравнение прямой, на которой лежит сторона АВ этого треугольника, можно записать в виде

(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0.

Подставим координаты третьей вершины С (х 3 ;у 3 ) в левую часть этого уравнения,

получим некоторое значение

q=(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )

Чтобы понять геометрический смысл числа q, заметим, что уравнение

(х-х 1 )(у 2 -у 1 )-(у-у 1 )(х 2 -х 1 )=q задает прямую, параллельную стороне АВ данного треугольника. Поэтому для каждой точки этой прямой результат подстановки ее координат в левую часть уравнения тот же, что и для точки C (х 3 ;у 3 ), и дает число q. Значит, то же значение получится и для точки С 1 (х 4 ;у 1 ) пересечения упомянутой прямой с прямой у=у 1 , параллельной оси абсцисс и проходящей через вершину A треугольника. Но в этой точке

(х-х 1 )(у 2 -у 1 )-(у-у 2 )(х 2 -х 1 ) = (х 4 -х 1 )(у 2 -у 1 ). Геометрический смысл последнего выражения понять уже несложно: |(х 4 -х 1 )(у 2 -у 1 )| площадь параллелограмма со сторонами АВ и АС 1 . Длина стороны АС 1 равна |х 4 -х 1 |, а длина высоты параллелограмма, опущенной из вершины B на эту сторону, есть |у 2 -у 1 |. Поэтому |q| есть площадь ΔАВС 1 , но она такая же, что и у ΔАВС. В результате приходим к следующей формуле для площади треугольника

S = |(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )|. (3, стр. 169).

Если треугольник задан в декартовой системе координат и имеет своими вершинами точки А (х 1 ;у 1 ), В (х 2 ;у 2 ), С (х 3 ;у 3 ), то можно составить уравнение треугольника:

|(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )| + |(x-x 2 )(y 3 -y 2 )-(y-y 2 )(x 3 -x 2 )| +

+ |(x-x 3 )(y 1 -y 3 )—(y-y 3 )(x 1 -x 3 )| = 2S, где

S = |(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )|.

Пример 3 . Составим уравнение треугольника, изображенного на рисунке. Для этого составим уравнения прямых, которые являются его сторонами, по формуле

(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0, задающей уравнение прямой по двум ее точкам. При этом допустимым считаем раскрытие скобок и приведение подобных слагаемых и недопустимым – умножение обеих частей уравнения на некоторое число (за исключением -1) .

Уравнения сторон имеют вид: х-у+1=0, х+у-1=0, 2у=0. Сложив модули левых частей этих уравнений, и приравняв полученное выражение к удвоенной площади ΔАВС, равной в данном случае 1, приходим к искомому уравнению |x-y+1|+|x+y-1|+2|y|=2.

Описанный метод дает возможность получить уравнение любого выпуклого многоугольника на плоскости, координаты вершин которого известны.

Уравнение квадрата, ромба

Пример 4 . Составить уравнение квадрата:

|x-1| + |y-1| + |x| + |y| = 1. Площадь равна 1.

Пример 5 . Составить уравнение ромба:

Через точки с координатами (1;0), (0;1) уравнение прямой: x +y -1 = 0.

Через точки с координатами (-1;0), (0;1) уравнение прямой: x – y + 1 = 0.

Через точки с координатами (-1;0), (0;-1) уравнение прямой: x + y + 1 = 0.

Через точки с координатами (0;-1), (1;0) уравнение прямой: -x + y + 1 = 0.

Получили: | x + y — 1| + | x – y + 1| + | x + y + 1| + | -x + y + 1 | = 4.

Этот же ромб имеет другое уравнение: |х| + |у| = 1, которое лучше решать «методом областей». Площадь ромба равна 2.

Пример 6 . Докажите, что уравнения: |x + y| + |x — y| = 2 и |x + 1| + |y + 1| + |x -1| +|y — 1| =4 относятся к одному квадрату.

Первое уравнение лучше решать «методом областей», где вся плоскость разбивается прямыми у =-х и у=х на четыре области, значит, искомая фигура четырехугольник, стороны которого параллельны осям координат. Из уравнений каждой области у=1, х=1и т.д. понимаем, что это квадрат, площадь которого равна 4.

Второе уравнение наглядно изображено, подтверждая первое.

Пример 7. Определить вид многоугольника по уравнениям:

|х| + 3|у| = 6; |х-3| + |у+3| = 3; |х-1| + 7|у| = 1.

Во всех случаях даны уравнения ромба .

Пример 8 . Изобразить на плоскости многоугольник по данному уравнению: |x|+|y|+|x+y|=4.

Из данного уравнения следует, что х=0, у=0, х= -у –прямые, которые разбивают плоскость на несколько областей.

Найдем уравнение прямой, стороны многоугольника, в каждой из областей:

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Найти четвертую вершину параллелограмма

Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?

В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.

Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.

Дано: ABCD — параллелограмм,

1) Найдём координаты точки O — середины диагонали AC.

2) По свойству диагоналей параллелограмма, точка O также является серединой BD:

Дано: ABCD — параллелограмм,

1) Ищем координаты точки O — середины отрезка BD:

2) Точка O также является серединой AC:

Видео:Уравнение окружности (1)Скачать

2 Comments

А как вы получили -14 в первом примере.

Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.

Видео:ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

Задачи на координатной сетке

Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Задачи на координатной сетке

Площадь фигур на координатной сетке или плоскости можно решить несколькими способами:

1. Достроить фигуру до прямоугольника или квадрата.

2. Найти площадь прямоугольника.

3. Найти площади всех дополнительных фигур (чаще всего это прямоугольные треугольники или трапеции).

4. Из площади прямоугольника вычесть все площади дополнительных фигур.

Найдите площадь четырёхугольника, вершины которого имеют координаты $(0;5), (4;7), (7;0), (11;2)$.

1. Достроим параллелограмм до прямоугольника

2. Найдем длину и ширину прямоугольника:

Чтобы найти длину стороны, параллельную какой либо оси, надо из большей координаты отнять меньшую координату.

Длина стороны $EF= 11$, стороны $FK= 7$. Подставим в формулу площади данные и сделаем вычисления: $S_= 11·7=77$.

3. Найдем площади дополнительных (ненужных) фигур:

4. Из площади прямоугольника вычтем все площади дополнительных фигур и таким образом получим площадь искомого параллелограмма.

• Второй способ

1. Если линии фигуры идут ровно по клеточкам и можно посчитать длины сторон, высот и т.д., то считаем клеточки и определяем величины.

2. Подставляем известные значения в формулу площади.

• Третий способ.

Площадь искомой фигуры можно найти по формуле Пика:

$S=/+В-1$, где $Г$ — количество узлов на границе фигуры (на сторонах и вершинах);

$В$ — количество узлов внутри фигуры.

Узел – это уголок клетки или пересечение линий

Найдите площадь четырёхугольника, изображённого на клетчатой бумаге с размером клетки $1 см × 1$ см. Ответ дайте в квадратных сантиметрах.

Отметим красными точками узлы на границе фигуры (Г), а желтыми – узлы внутри фигуры (В).

Подставим данные в формулу Пика: $S=/+6-1=3.5+6-1=8.5$

Площади некоторых фигур

Площадь треугольника:

1. $S=/$, где $h_a$ — высота, проведенная к стороне $а$
2. Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.
3. Для равностороннего треугольника $S=<a^√3>/$, где $а$ — длина стороны.

Площади четырехугольников:

1. Прямоугольник $S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб $S=/$, где $d_1$ и $d_2$ — диагонали ромба
3. Трапеция $S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
4. Квадрат $S=a^2$, где $а$ — сторона квадрата.
5. Параллелограмм $S=a·h_a$, где $h_a$ — высота, проведенная к стороне $а$.

Площадь круга:

$S=π·R^2$, где $π=3.14, R$ — радиус окружности.

Площадь сектора:

$S=<S_n°>/=/$, где $n°$ — это градусная мера центрального угла, отсекающего заданный сектор.

Площадь кольца:

В прямоугольнике и квадрате центр описанной окружности лежит в точке пересечения диагоналей, а радиус описанной окружности равен половине диагонали.

В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы и радиус равен половине гипотенузы.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

В прямоугольном треугольнике $АВС$ для острого угла $В$:

Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

$cos BOA= — cos BOC$;

$ctg BOA= — ctg BOC$.

Углы в окружности.

1. Угол, образованный двумя радиусами, называется центральным. Центральный угол равен градусной мере дуги, на которую он опирается.

2. Угол, вершина которого лежит на окружности, а стороны являются хордами, называется вписанным. Вписанный угол равен половине градусной меры дуги, на которую он опирается

Найдите величину угла MPK. Ответ дайте в градусах.

Угол $МРК$ равен половине градусной меры дуги $МК$, так как он вписанный. Чтобы отыскать градусную меру дуги, посмотрим, на сколько таких дуг мы можем разделить всю окружность, потом $360°$ разделим на полученное количество.

Дуга $МК$ отсекается хордой, занимающей две клетки. Разделим такими хордами всю окружность, получилось $8$ дуг.

$360:8=45°$, составляет градусная мера дуги $МК$.

Прямые на координатной плоскости

Координаты середины отрезка равны среднему арифметическому координат его концов.

Найдите абсциссу середины отрезка, соединяющего точки $В(2;8)$ и $A(6;4)$.

Пусть точка $М$ – середина отрезка $ВА$. Чтобы найти абсциссу данной точки, надо найти среднее арифметическое абсцисс концов отрезка:

Уравнение прямой, проходящей через две заданные точки на плоскости имеет вид $y=kx+b$, где $k$ и $b$ – это коэффициенты.

Уравнение можно задать с помощью формулы:

Точки пересечения прямой с осями координат:

Если прямая пересекает ось Ох, то в уравнении прямой координата $у = 0$, а если прямая пересекает ось Оу, то уравнении прямой координата $х = 0$.

Две прямые на координатной плоскости будут параллельны, если в уравнениях прямых будут равны коэффициенты k.

Если уравнение первой прямой: $y=k_x+b_1$;

Уравнение второй прямой: $y= k_x+b_2$, то при параллельности прямых, $k_1=k_2$.

🎬 Видео

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Угол между векторами | МатематикаСкачать

Линейное уравнение в координатной плоскости.Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Составляем уравнение прямой по точкамСкачать

8 класс, 4 урок, ПараллелограммСкачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Векторы. Метод координат. Вебинар | МатематикаСкачать

Векторы в координатной плоскости.Скачать

Видеоурок "Канонические уравнения прямой"Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать