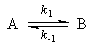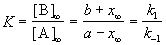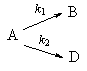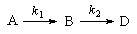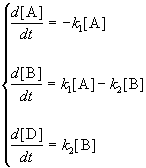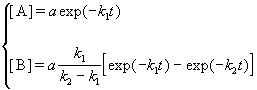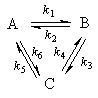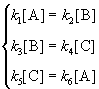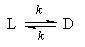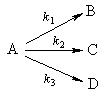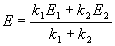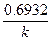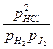Уравнение параллельной реакции первого порядка (7 видео)

Уравнение параллельной реакции первого порядка

При изучении кинетики сложных реакций, включающих несколько элементарных стадий, используют принцип независимости химических реакций:

Если в системе протекает несколько простых реакций, то каждая из них подчиняется основному постулату химической кинетики независимо от других реакций.

Основные типы сложных реакций мы рассмотрим на примере реакций первого порядка.

1. Обратимые реакции первого порядка:

Закон действующих масс записывается следующим образом:

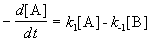
Если начальные концентрации веществ A и B обозначить, соответственно, a и b и ввести степень превращения x ([A] = a — x, [B] = b + x), то кинетическое уравнение приобретает вид:

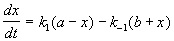
Решение этого уравнения можно выразить через степень превращения, соответствующую достижению равновесия:

или , (5.1)

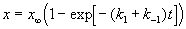
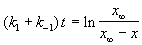
где xопределяется условием равенства скоростей прямой и обратной реакций:

, откуда следует: . (5.2)

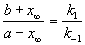
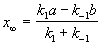
При t наступает равновесие, которое характеризуется константой:

2. Параллельные реакции первого порядка:

Кинетическое уравнение записывается с учетом принципа независимости:

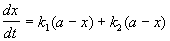
Решение этого уравнения записывается так же, как и для одной реакции первого порядка:

, . (5.3)

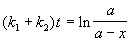
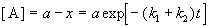
Для параллельных реакций в любой момент времени отношение концентраций продуктов постоянно и определяется константами скорости элементарных стадий:

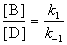
3. Последовательные реакции первого порядка:

Пусть в начальный момент времени есть только вещество A. Применим к этой системе закон действующих масс и принцип независимости химических реакций:

Решение этой системы дает концентрации веществ:

Концентрация промежуточного вещества достигает максимума при

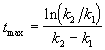
Величина этого максимума определяется отношением констант k₂ / k₁. Если оно велико, т.е. k₂ >> k₁, то промежуточный продукт не успевает накапливаться и его концентрация в любой момент времени мала. В этом случае для анализа кинетических уравнений можно использовать приближенный метод квазистационарных концентраций ( 6).

Пример 5-1. Для обратимой реакции первого порядка

K_равн = 8, а k₁ = 0.4 с -1 . Вычислите время, при котором концентрации веществ A и B станут равными, если начальная концентрация вещества B равна 0.

Решение. Из константы равновесия находим константу скорости обратной реакции:

с -1 .

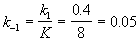
По условию, мы должны найти время, за которое прореагирует ровно половина вещества A. Для этого надо подставить значение x(t) = a/2 в решение кинетического уравнения для обратимых реакций (5.1) и (5.2):

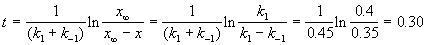
Пример 5-2. В параллельных реакциях первого порядка

выход вещества B равен 63%, а время превращения A на 1/3 равно 7 минутам. Найдите k₁ и k₂.

Решение. Кинетическое уравнение (5.3) для разложения вещества в параллельных реакциях имеет вид уравнения первого порядка, в которое вместо одной константы скорости входит сумма констант скорости отдельных стадий. Следовательно, по аналогии с реакциями первого порядка, по времени превращения A на 1/3 (x(t) = a/3) можно определить сумму констант k₁ + k₂:

мин -1 .

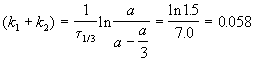
Выход вещества В равен 63%, а вещества D — 37%. Отношение этих выходов равно отношению конечных концентраций веществ B и D, следовательно оно равно отношению соответствующих констант скорости:

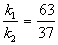
Решая это уравнение совместно с предыдущим, находим: k₁ = 0.037 мин -1 , k₂ = 0.021 мин -1 .

Пример 5-3. Имеется следующее равновесие:

Как связаны между собой константы k₁ — k₆?

Решение основано на принципе детального равновесия:

Если сложная система находится в равновесии, то в каждой из элементарных стадий также соблюдается равновесие.

Это означает, что во всех трех процессах: A B, B C и C A скорости прямой и обратной реакций равны:

Перемножив почленно эти три равенства и поделив левую и правую части на произведение равновесных концентраций [A] . [B]. [C], находим искомое соотношение между константами скорости:

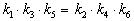
5-1. Нарисуйте графики зависимости концентраций веществ A и B от времени в обратимой реакции A B для двух случаев: 1) k₁ > k_-1; 2) k₁ -1 . Вычислите время, при котором концентрации веществ A и B станут равными, если начальная концентрация вещества B равна 0.(ответ)

5-5. Превращение роданида аммония NH₄SCN в тиомочевину (NH₄)₂CS — обратимая реакция первого порядка. Рассчитайте константы скорости прямой и обратной реакций, используя следующие экспериментальные данные:

t, мин

Доля прореагировавшего NH₄SCN, %

5-6. Один из методов оценки возраста биологических объектов основан на измерении содержания в них оптических изомеров аминокислот. В живых организмах отношение концентраций D- и L-изомеров постоянно ([D]₀ / [L]₀ = a). В мертвых организмах происходит рацемизация:

Чему равен возраст биологического объекта, в котором [D] / [L] = b? Решите задачу в общем виде и для образца, содержащего аспарагиновую кислоту (k = 1.48 . 10 -5 лет -1 , a = 0.07, b = 0.27).(ответ)

5-7. В параллельных реакциях первого порядка

выход вещества B равен 53%, а время превращения A на 1/3 равно 40 c. Найдите k₁ и k₂.(ответ)

5-8. Реакция разложения вещества А может протекать параллельно по трем направлениям:

Концентрации продуктов в смеси через 5 мин после начала реакции были равны: [B] = 3.2 моль/л, [C] = 1.8 моль/л, [D] = 4.0 моль/л. Определите константы скорости k₁ — k₃, если период полураспада вещества А равен 10 мин.(ответ)

5-9. Реакция разложения вещества А может протекать параллельно по трем направлениям:

Концентрации продуктов в смеси через 10 мин после начала реакции были равны: [B] = 1.6 моль/л, [C] = 3.6 моль/л, [D] = 7.8 моль/л. Определите константы скорости k₁ — k₃, если период полураспада вещества А равен 8 мин.(ответ)

5-10. Покажите, что при двух параллельных реакциях

энергия активации суммарной реакции разложения A связана с энергиями активации отдельных стадий следующим образом:

*5-11. В системе идут две параллельные газофазные реакции: А + B C (k₁), A D (k₂). Исходная смесь эквимолекулярна, начальное давление составляет 200 мм рт. ст. При практически полном превращении А при 227 о С Р_С = 10 мм рт.ст., а при 327 о С Р_С = 39 мм рт.ст. Найдите разность энергий активации этих реакций.(ответ)

5-12. На одном графике нарисуйте зависимости концентрации вещества B от времени в системе последовательных реакций A B D для двух случаев: 1) k₁ >> k₂; 2) k₁ > 1; 2) k₂ / k₁

[предыдущий раздел]

[содержание]

[следующий раздел]

Уравнение параллельной реакции первого порядка

Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору

Видео:Как расставлять коэффициенты в уравнении реакции? Химия с нуля 7-8 класс | TutorOnlineСкачать

Уравнение параллельной реакции первого порядка

Из уравнений (4) и (5) видно, что критериями первого порядка реакции по реагенту А является линейная зависимость ln [ A ] – t или ln – t

В тоже время по тангенсам углов наклона линейных зависимостей можно определить константы скорости.

Другой тест правильности выбранного первого порядка является постоянство константы скорости реакции, вытекающее из уравнения (5)

Размерность константы скорости первого порядка dim = [1/ c ], [1/мин] или соответственно с -1 , мин -1

Третий тест основан на концентрационной зависимости времени полупревращения. Условие полупревращения [ A ] = 0,5[ A ]₀ , тогда в соответствии с уравнением (5)

Можно видеть, что критерием первого порядка реакции является независимость времени полупревращения t _½ от начальной концентрации реагента [ A ]₀.

Примерами подобных реакций первого порядка являются реакции изомеризации, а также реакции разложения некоторых сложных молекул в газовой фазе.

и в жидкой фазе, например, гидролиз трет-бутилбромида.

Для реакции A + B → C + D можно записать уравнение скорости

Обозначим [ A ]₀ и [ B ]₀ – начальными концентрациями реагентов А и В, а Х – количество прореагировавших А и В, тогда уравнение (1) приобретет вид

Разделяя переменные, имеем

Проинтегрируем левую часть этого уравнения методом неопределенных коэффициентов, для чего представим дробь

в виде суммы дробей

Решая совместно эти уравнения, имеем

Подставляя значения α и β в уравнение (3) и (4) и интегрируя полученные уравнения в соответствующих пределах

Из уравнения (5) видно, что критерием правильности выбранного второго порядка реакции является линейность зависимости

от времени.

По тангенсу угла наклона этой зависимости можно определить константу скорости реакции. Другим критерием правильности выбранного второго порядка является постоянство значений k , вычисленных в соответствии с уравнением (5):

во всем диапазоне пар значений τ – х.

Размерность константы скорости второго порядка

или, соответственно, л·моль -1 ·с -1 , л·моль -1 ·мин -1 .

Если вещества А и В взяты в равных количествах или реакция идет с участием одного вещества, например

то при постоянстве объема удобно использовать в качестве переменной концентрацию одного из исходных веществ

тогда кинетическое уравнение будет иметь вид

Интегрируя это уравнение в соответствующих пределах

приходим к выражению

Из уравнений (7) и (8) следует, что критериями правильности выбранного второго порядка являются линейный характер зависимости 1/[ A ] от t и постоянство значения k , вычисленных для различных пар значений [ A ] – t по формуле

Третий критерий правильности второго порядка основан на определении времени полупревращения t _½ _. Так как [ A ] = 0.5[ A ]₀, то в соответствии с уравнением (7)

, откуда

Можно видеть, что критерием второго порядка является обратно пропорциональная зависимость между t _½ и начальной концентрацией реагента. В соответствии с выражениями (7) и (8) константы скорости второго порядка можно определить по тангенсу угла наклона зависимостей или от времени.

Имеется множество реакций протекающих по кинетике второго порядка:

и простой случай, соответствующий равенству исходных и текущих концентраций реагентов

Разделяя переменные и интегрируя

Из уравнения (3) видно, что критериями правильности выбранного третьего порядка является линейность зависимостей или от t , постоянства значения k , вычисленное по формуле

для всех пар значений t и [ A ] и обратно пропорциональная зависимость между временем полупревращения и квадратом начальной концентрации реагента

В соответствии с уравнением (3) константа скорости третьего порядка может быть определена по тангенсу угла наклона зависимости или от времени.

Интегрирование уравнения (1)

приводит к выражениям

Из уравнений (2) и (3) следует, что критериями нулевого порядка по реагенту А являются линейный характер зависимости [ A ] от t , постоянство k , вычисленного по формуле

во всем диапазоне пар значений t – A и прямолинейная зависимость между временем полу превращения и начальной концентрацией реагента

Из уравнений (2) и (3) следует, что константа скорости нулевого порядка может быть определена по тангенсу угла наклона зависимостей [ A ]₀ – [ A ] или [ A ] от времени

Сложные реакции представляют собой совокупность простых реакций. К сложным реакциям относятся обратимые реакции.

При кинетическом анализе сложных реакций руководствуются принципом независимости простых реакций, согласно которому каждая простая реакция, входящая в сложную ведет себя кинетически так, как если бы она была единственная.

в начальный момент времени концентрация реагента A составляет [ A ]₀, а [ B ] = 0, то уравнение этой реакции запишется как

Выражая r через концентрацию [A] имеем

= k₁<[A]₀ – X> – k_-1X

где X – количество молей вещества A в единице объеме, которое прореагировало к моменту τ и соответственно количество молей вещества B в единице объеме, которое образовалось к этому моменту. Преобразуя правую часть уравнения (2)

= k₁[A]₀ – (k-₁ + k₁)X

В условиях равновесия

При τ ® ¥ X стремится к своему равновесному значению X ® X _¥ . Тогда

где

Тогда кинетическое уравнение (3) примет вид

Интегрируя это уравнение в соответствующих пределах

В соответствии с выражениями (6) и (7) кинетические зависимости для A и B будут иметь следующий вид

Пользуясь интегральной формой кинетического уравнения (5) и соотношением можно на основе кинетических данных определить значения констант скоростей k ₁ и k _-1

Так, в соответствии с (5)

так как , то

Подставляя последнее выражение в уравнение (8), имеем

Подставляя выражение (10) в уравнение (8), имеем

Рассмотрим систему параллельных реакций первого порядка

В соответствии с ранее принятыми обозначениями суммарная скорость расходования реагента A выразится уравнением

По форме уравнение (1) подобно кинетическому уравнению необратимой реакции первого порядка, поэтому его интегральная форма имеет вид.

Разрешая уравнение (2) относительно [ A ] имеем

Для определения констант k ₁ и k ₂ рассмотрим уравнения конкурирующих параллельных реакций.

Поделив почленно, левые и правые части уравнений (5) и (6), имеем уравнение , интегрирование которого приводит к равенству

Разделяя, левые и правые части уравнений (5) и (1), (6) и (7), приходим к очевидным равенствам

интегрирование которых дает уравнения:

Подставляя в последние уравнения выражение (4) приходим к равенствам

Уравнения (2) и (8) являются основой для определения абсолютных значений констант скорости конкурирующих реакций k ₁ и k ₂ . На первом этапе можно определить сумму констант скоростей k ₁ + k ₂ , пользуясь уравнением (2). Затем на основе линейных зависимостей между X_B и X , а также X_C и X определяют брутто константы и , из которых рассчитывают k ₁ и k ₂ по ранее определенному значению суммарной константы скорости k ₁ + k ₂ .

Нетрудно показать, что для трех параллельных реакций первого порядка

Этот случай более сложен по сравнению с предыдущим. Рассмотрим систему параллельных реакций

Уравнение скорости расхода A в этой системе реакций с учетом его количества, прореагировавшего к моменту времени t (Х) имеет вид:

или с учетом преобразований

обозначая , имеем

Разделяя переменные, приходим к выражению

Интегрируем левую часть уравнения (3) методом неопределенных коэффициентов, для чего представим левую её часть в виде суммы дробей.

или

так как , то и

Тогда и

Откуда и ,

С учетом (4) возвращаемся к уравнению (3)

Интегрирование уравнения (5) приводит к выражению

Откуда

или

Возвращаясь к соотношению преобразуем (6) в равенство

Рассмотрим систему двух последовательных реакций первого порядка

В силу принципа независимости скорости расходования реагента A выражается уравнением скорости необратимой реакции первого порядка

Решение которого дается в виде

, и

Уравнение скорости изменения концентрации промежуточных продуктов

Разделим почленно левые и правые части уравнений (3) и (1)

Уравнение (4) имеет признаки однородного уравнения первого порядка. Для его решения вводим обозначение

Подставляя последнее выражение в уравнение (4), имеем:

Разделяем переменные и интегрируем

тогда

или

Так как , то уравнение (5) можно выразить в форме

В тоже время в соответствии с уравнением (2)

Тогда уравнение (5) можно преобразовать в форму

Выведенные зависимости показывают, что в случае необратимых последовательных реакций уравнение для первого промежуточного продукта связано с характеристиками лишь первых двух стадий, оставаясь одинаковым при любом числе и характеристиках последующих стадий. При этом независимо от начальной концентрации реагента A , значение второй характеристики материального баланса укладывается на одну кривую, если её изображать как функцию Х_А или t .

Используя уравнение (5) можно найти по экспериментальным данным путем подбора и зная, на основе кинетически исчерпывания A величину k ₁ – определить k ₂ .

Из анализа уравнения (6) следует, что при X_A = 0 и X_A = 1 , что говорит о наличии максимума . Его положение можно найти, приравнивая к нулю соответствующую производную

откуда

и значение максимума

Из выражений (8) и (9) видно, что положение и величина максимума промежуточного продукта в необратимых реакциях первого порядка зависит только от соотношения констант скоростей первых двух стадий. При этом, чем больше величина , тем ниже максимум и тем больше его положение смещается в сторону более низких степеней превращения (и наоборот). Очевидно, что по экспериментальному положению максимума можно определить по специальным номограммам или по уравнению (8) значение и использовать его в дальнейшем для описания значений концентраций B во времени согласно уравнению (7)

Уравнение образования продукта C :

Максимальная скорость соответствует точке перегиба на зависимости [ C ] от t и определяется из условия

Легко видеть, что это условие соответствует одновременно условию максимума концентрации B , определяемого уравнениями(8) и (9). Качественно проанализированные зависимости могут быть представлены графически.

Неэлементарные реакции состоят из ряда элементарных стадий, составляющих их механизм. Кинетика таких реакций определяется последовательностью элементарных стадий, их характером (обратимые, необратимые), природой реагентов, интермедиатов и продуктов реакции. При кинетическом анализе неэлементарных реакций возникает задача определения концентраций интермедиатов, играющих ключевую роль в образовании продуктов или расходовании реагентов. В качестве инструмента такого определения используется принцип квазистационарных концентраций Боденштейна – Семенова. Согласно этому принципу скорость изменения концентраций нестабильных интермедиатов пренебрежимо мала по сравнению со скоростью изменения концентраций реагентов и продуктов реакции и её можно считать равной нулю. Применение принципа стационарных концентраций к неэлементарным реакциям, протекающим по сложному механизму, позволяет исключить из кинетического описания процессов неизвестные концентрации интермедиатов и получить одно или некоторый минимум дифференциальных уравнений скорости, выраженных через подлежащие измерению концентрации реагентов и продуктов реакции.

Рассмотрим пример неэлементарной реакции, описываемой стехиометрией

и протекающей через образование интермедиата Q

Скорость реакции можно приравнять к скорости образования продукта B

В соответствии с принципом квазистационарных концентраций

откуда

Подставляя последнее выражение в уравнение (1) приходим к уравнению скорости реакции

Если экспериментально возможно непосредственно измерить скорость реакции, то обработку кинетических данных можно провести, преобразуя уравнение (3) как:

Последнее уравнение приводится к виду

Обрабатывая зависимость (4) в координатах по ординате находят k ₁ , а по тангенсу угла наклона . Полученных констант достаточно для кинетического описания реакции, так как, разделив числитель и знаменатель уравнения (3) на k ₂ , приходят к уравнению

Видео:Физическая химия #3. Первый, второй и третий порядки химической реакции. Времена полупревращенияСкачать

Реакции первого порядка

Кинетическое уравнение реакции первого порядка имеет вид:

v = — 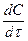= kC

гдe c — концентрация реагента.

Преобразовав уравнение, получим:

— = kdt

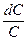
и после интегрирования:

Обозначив начальную концентрацию как C_o (когда t=0) можно определить константу интегрирования B: B = lnC₀

lnC = -kt + lnC₀ Þ (подставив lnC₀) lnC — lnC₀ = -kt Þ ln 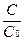= -kt

или (если найти антилогарифм): 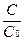=exp(-kt) and C= C₀×exp(-kt)

Диаграмма, где концентрация реагента представлена на оси ординат, время реакции — на оси абсцисс:

Представим, что нужно определить время, когда C= C₀/2 (концентрация исходного вещества упадет в 2 раза)

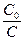
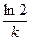
ln = ln2 = -kt, t= =

Эта зависимость показывает, что константа скорости реакции 1-го порядка обратно пропорциональна времени (периоду) полураспада.

Период полураспада (t_1/2) равен времени, в течение которого прореагирует половина первоначального количества вещества.

Также можно получить подобные уравнения для (t_1/2) для реакций более высокого порядка, но это более сложно.

Порядок реакций не равен их молекулярности если :

a) Один из реагентов присутствует в таком большом избытке, что его расход практически не будет изменять его концентрацию. Например, гидролиз эфира в разбавленном водном растворе:

Концентрация воды изменяется пренебрежимо мало, и скорость реакции будет зависеть только от изменения концентрации эфира. В результате скорость реакции будет описываться уравнением 1-го порядка, хотя это бимолекулярная реакция.

b) Если это сложная реакция. Обычно в этом случае уравнение химической реакции отражает только общий эффект всех взаимодействий

Молекулярность равна 2. Реакция имеет 2 стадии:

1-я стадия — медленнее и определяет скорость суммарной реакции, поэтому v=kC_N₂_O₅ и порядок реакции равен 1. Если одна из стадий проходит при низкой, по отношению к другим, скорости, то суммарная скорость реакции будет определяться скоростью этой стадии. Эта стадия называется — лимитирующая стадия реакции.

c) Для гетерогенных реакций, например:

2Zn + O₂ = 2ZnO. Молекулярность реакции равна 3, но кинетика реакции описывается уравнением реакции 1-го порядка: v= k×C_O₂,

потому что Zn — это твердое вещество, у него нет концентрации, но O₂ — газ, ему соответствует определенная концентрация.

Сложные реакции

Кинетика сложных реакций, состоящих из 2-х и более простых реакций, взаимосвязанных друг с другом тем или иным способом, зависит от природы этой взаимосвязи и отношения скоростей простых реакций. Типичные формы взаимосвязи простых реакций, когда они являются параллельными, последовательными (консекутивные), сопряженными и обратимыми реакциями.

Теория кинетики сложных реакций основана на принципе, что когда несколько реакций происходят одновременно и каждая идет независимо и кинетика каждой реакции может быть описана кинетическим уравнением простой реакции.

Параллельные реакции — это реакции вида:

В таких реакциях начальное вещество (или вещества) могут реагировать параллельно в различных направлениях.

Последовательные реакции -реакции вида:

где B — промежуточный продукт в образовании C и k₁ и k₂ — константы скорости 2-х стадий реакции.

Сопряженные реакции — реакции типа:

A + B ® M

В которых одна, например 1-я, происходит только вместе со 2-й, т.е. индуцируется 2-й.

Обратимые реакции. Скорость обратимой реакции равна разности между скоростями прямой и обратной реакций.

если написать выражения для скоростей прямой и обратной реакций:

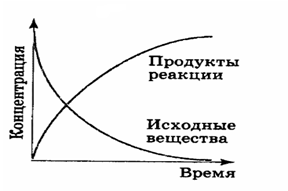
Если в системе первоначально присутствуют только реагенты (H₂ и J₂), скорость прямой реакции v₁ (Исходные вещества) будет уменьшаться с уменьшением концентраций этих компонентов.

Кривая v₂ (Продукты реакции) начинается в начале координат (поскольку по условию первоначально C_HJ = 0) и возрастает по мере того, как реакция идет.

Положение равновесия будет достигнуто, когда абсолютное значение скоростей прямой и обратной реакций будет равным: v₁ = v₂ и результирующая скорость = 0.

Если переписать соотношение и затем преобразовать его:

= = K_c

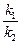
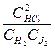
где K_c — концентрационная константа равновесия реакции.

Если предыдущее уравнение применять к реакциям, проходящим в не очень разбавленных растворах, мы должны заменить концентрации веществ их активностями, и тогда заменить K_c на K_a.

Если уравнение применять к смеси идеальных газов мы должны заменить концентрации — парциальными давлениями газов, и соответственно K_c на K_p:

K_p=

гдe p_HCl_, p_H_2, p_J₂ — парциальные давления газов. Парциальное давление газа, находящегося в смеси других газов, равно давлению, которое этот газ производил, если бы он при данной температуре занимал весь объем, занимаемый смесью газов. В общем случае K_p ¹ K_c. Если применить уравнение для идеальных газов, можно найти зависимость между K_p и K_c.

p_i = 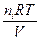= C_i RT

где n_i — количество молей газообразного компонента i, C_i — концентрация газа.

Tогда для вышеприведенной реакции:

K_p= 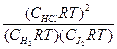= K_c (RT).

В общем случае: K_p = K_c (RT) D n ,

гдe Dn -разность между стехиометрическими коэффициентами газообразных продуктов реакции и реагентов (Для реакции (H₂ and J₂) Dn=0 and K_p = K_c)

Константа равновесия — важная характеристика реакции, по ее величине можно судить о степени протекания реакции (большое значение — реакция сдвинута в сторону продуктов реакции, низкое — в сторону исходных веществ). Константа не зависит от концентраций (давлений), зависит от температуры.

Если переписать уравнение реакции в общем виде:

aA + bB = cC + dD +eE

и вещества A, B, C and D — газы, а E — жидкость или твердое вещество, тогда:

Dn= c + d –a –b

Для условий: реакция проходит при постоянной температуре и постоянных парциальных давлениях для всех веществ, и законы идеальных газов применимы, существует связь между энергией Гиббса и константой химического равновесия K_p:

Таким образом, можно вычислить значение K_p