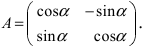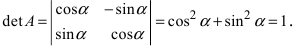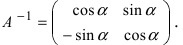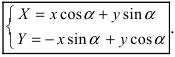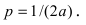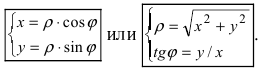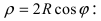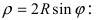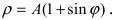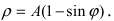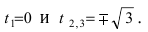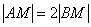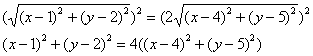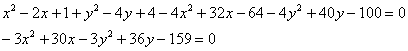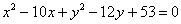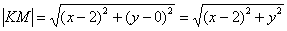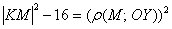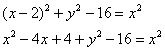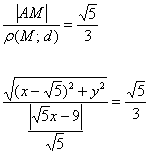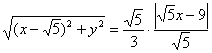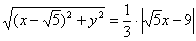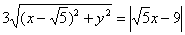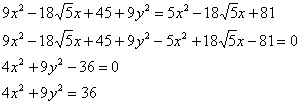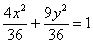Содержание:
- Преобразования декартовой системы координат
- Параллельный перенос и поворот системы координат
- Полярные координаты. Замечательные кривые
- Параллельный перенос и поворот
- Параллельный перенос
- Поворот
- Готовые работы на аналогичную тему
- Примеры задач на параллельный перенос и поворот
- Поворот и параллельный перенос параболы
- 📺 Видео
Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Преобразования декартовой системы координат
Параллельный перенос и поворот системы координат
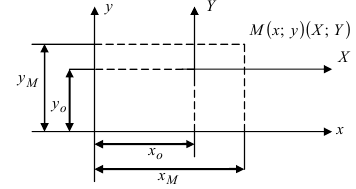
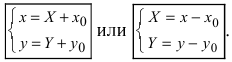
1. Параллельный перенос системы координат. Пусть на плоскости две декартовы системы координат, причем соответствующие оси параллельны и сонаправлены (Рис.46):
Рис. 46. Параллельный перенос одной системы координат относительно другой системы.
Систему координат 
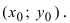
Пример:
Дана точка М(3;2) и начало новой системы координат 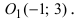
Решение:
Используя формулы, определяющие параллельный перенос одной системы отсчета относительно другой, получим 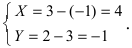
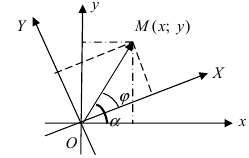
2. Поворот системы координат. Пусть даны две системы координат (старая и новая), имеющие общее начало отсчета и повернутые относительно друг друга на угол 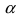
Рис. 47. Поворот одной системы координат относительно другой системы с общим началом координат двух систем.
Получим формулы, связывающие старые и новые координаты произвольной точки М(х; у). Из рисунка видно, что в новой системе координат координаты точки равны 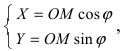
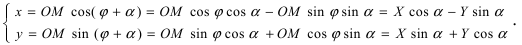
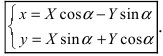
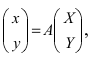
Найдем обратное преобразование системы координат, найдем матрицу 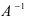
Найдем алгебраические дополнения всех элементов
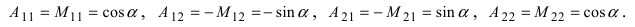
Определение: Унитарными преобразованиями называются такие преобразования, для которых определитель матрицы преобразования равен 1.
Определение: Ортогональными преобразованиями называются такие преобразования, для которых обратная матрица к матрице преобразования совпадает с транспонированной матрицей преобразования.
Таким образом, имеем 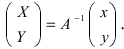
Пример:
Найти координаты точки М(1; 2) в новой системе координат, повернутой относительно старой системы отсчета на угол
Решение:
Воспользуемся полученными формулами 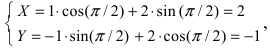
Рассмотрим применение преобразования координат:
а) Преобразовать уравнение параболы 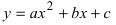
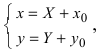
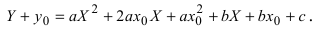
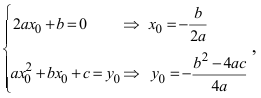
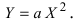
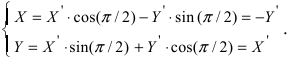
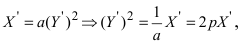
Пример:
Преобразовать уравнение параболы 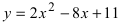
Решение:
Найдем начало отсчета новой системы координат после параллельного переноса 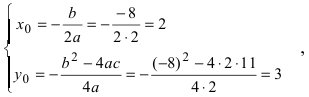
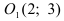
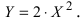
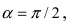
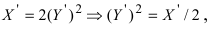
б) Выяснить, какую кривую описывает функция
Проведем следующее преобразование 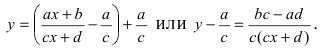
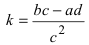
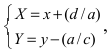
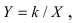
Полярные координаты. Замечательные кривые
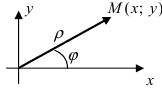
Пусть полярная ось совпадает с осью абсцисс Ох, а начало полярной оси (полюс полярной системы координат) совпадает с началом координат декартовой системы отсчета (Рис. 48). Любая точка М(х;у) в полярной системе координат характеризуется длиной радиус-вектора, соединяющего эту точку с началом отсчета и углом 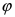
Рис. 48. Полярная система координат.
Главными значениями угла 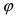
Рассмотрим замечательные кривые в полярной системе координат:
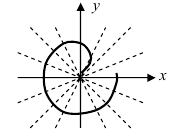
1. Спираль Архимеда 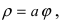
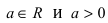
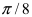
Рис. 49. Спираль (улитка) Архимеда.
2. Уравнение окружности: уравнение 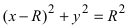
Рис. 50. Окружность с центром в точке A(R; 0) и радиусом R.
3. Уравнение 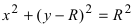
Рис. 51. Окружность с центром в точке А(0; R) и радиусом R.
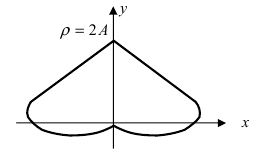
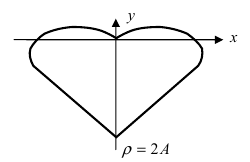
4. Кардиоиды:
Рис. 52. Кардиоида
Рис. 53. Кардиоида
Аналогично выглядят кардиоиды 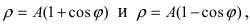
5. Петля: 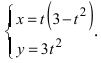
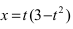
Для первого корня у = 0, а для второго и третьего — у = 9 . Следовательно, петля имеет вид
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Бесконечно малые и бесконечно большие функции
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Экстремум функции
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Видеоурок "Преобразование координат"Скачать

Параллельный перенос и поворот
Вы будете перенаправлены на Автор24
Видео:Поворот и параллельный перенос координатных осей. ЭллипсСкачать
Параллельный перенос
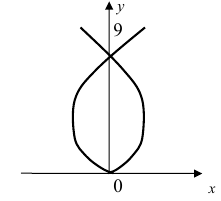
Введем определение параллельного переноса на вектор. Пусть нам дан вектор $overrightarrow$.
Рисунок 1. Параллельный перенос
Введем следующую теорему.
Параллельный перенос является движением.
Доказательство.
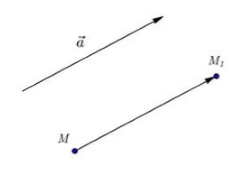
Пусть нам даны точки $M и N$. Пусть при их параллельном переносе на вектор $overrightarrow$ эти точки отображаются в точки $M_1$ и $N_1$, соответственно (рис. 2).
Рисунок 2. Иллюстрация теоремы 1
Значит четырехугольник $_1N_1N$ — параллелограмм и, следовательно, $MN=M_1N_1$. То есть параллельный перенос сохраняет расстояние между точками. Следовательно, параллельный перенос является движением.
Теорема доказана.
Видео:§35 Формулы поворота координатных осейСкачать

Поворот
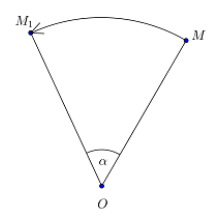
Введем определение поворота вокруг точки $O$ на угол $alpha $.
Поворот вокруг точки $O$ на угол $alpha $ — отображение плоскости на себя, при котором любая точка $M$ отображается на точку $M_1$ такую, что $_1=OM, angle M_1=angle alpha $ (Рис. 3).
Рисунок 3. Поворот
Готовые работы на аналогичную тему
Введем следующую теорему.
Поворот является движением.
Доказательство.
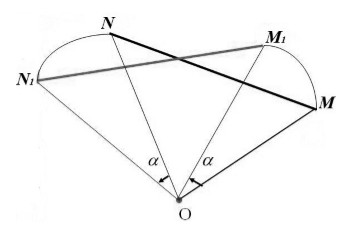
Пусть нам даны точки $M и N$. Пусть при их повороте вокруг точки $O$ на угол $alpha $ они отображаются в точки $M_1$ и $N_1$, соответственно (рис. 4).
Рисунок 4. Иллюстрация теоремы 2
Так как, по определению 2, $_1=OM, _1=ON$ и $overrightarrow<_1>=overrightarrow$, а ,$angle MON=angle M_1ON_1$, то
Следовательно, $MN=M_1N_1$. То есть поворот сохраняет расстояние между точками. Следовательно, поворот является движением.
Теорема доказана.
Видео:Геометрия 9 класс : Параллельный перенос и поворотСкачать

Примеры задач на параллельный перенос и поворот
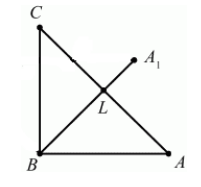
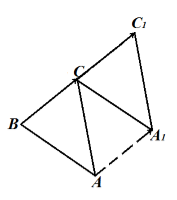
Построить треугольник $A_1B_1C_1$,образованный поворотом вокруг точки $B$ на угол $^0$ равнобедренного прямоугольного (с прямым углом $B)$ треугольника $ABC$.
Решение.
Очевидно, что точка $B$ перейдет сама в себя, то есть $B_1=B$. Так как поворот производится на угол, равный $^0$, а треугольник $ABC$ равнобедренный, то прямая $BA_1$ проходит через точку $L$ — середины стороны $AC$. По определению, отрезок $BA_1=BA$. Построим его (Рис. 5).
Построим теперь вершину $C_1$ по определению 2:
[angle CBC_1=^0, BC=BC_1]
Соединим все вершины треугольника $A_1B_1C_1$ (Рис. 6).
Решение закончено.
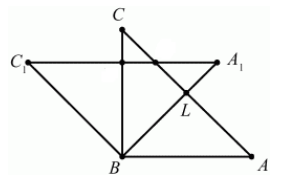
Построить параллельный перенос треугольника $ABC$ на вектор $overrightarrow$.
Решение.
Перенесем каждую вершину треугольника на вектор $overrightarrow$. Получаем треугольник $CA_1C_1$ (рис. 7).
Решение закончено.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 15 04 2021
Видео:Геометрия 9 класс (Урок№30 - Поворот.)Скачать

Поворот и параллельный перенос параболы
Парабола – одна из самых распространённых линий в математике, и строить её придётся действительно часто. Поэтому, пожалуйста, особенно внимательно отнестись к заключительному параграфу урока, где я разберу типовые варианты расположения данной кривой.
! Примечание: как и в случаях с предыдущими кривыми, корректнее говорить о повороте и параллельном переносе координатных осей, но автор ограничится упрощённым вариантом изложения, чтобы у читателя сложились элементарные представления о данных преобразованиях.
1) Поворот вокруг вершины. Если в уравнении присутствует знак «минус»: 


На следующем чертеже изображены графики кривых 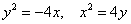
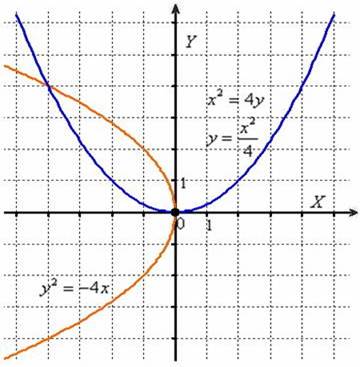
Оба уравнения задают неканоническое расположение нашей подопытной параболы 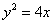
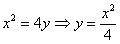
Таким образом, все параболы, с которыми мы обычно работаем – не каноничны! Я очень хотел «уложить на бок» классическую параболу 

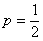
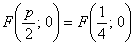
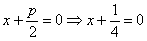
2) Параллельный перенос. Без всякой оригинальности. Уравнение 

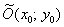

Соответствующее творческое задание для самостоятельного решения:
Построить параболу 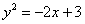
Как лучше действовать?
По условию требуется построить параболу 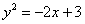


Вторая часть задания предполагает приведение уравнения к каноническому виду. Проанализируйте равенство 

Ну, а наша обзорная экскурсия подошла к концу, и я надеюсь, что у вас не возникло и не возникнет трудностей с тремя атлантами темы – эллипсом, гиперболой и параболой. Предлагаю узнать новый теоретический материал и закрепить практические навыки на урокеЗадачи с линиями 2-го порядка.
Решения и чертежи:
Пример 5: Решение: данная гипербола является равносторонней, поэтому имеет асимптоты 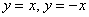
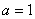


Определим координаты фокусов: 

Выполним чертёж:
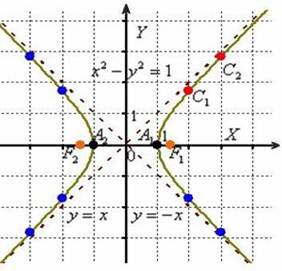
Перед вами «школьная» гипербола в каноническом положении. График функции 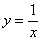

И в общем случае – график обратной пропорциональности 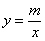
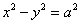
Пример 7: Решение: преобразуем уравнение:

Вершина параболы находится в точке 
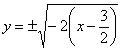
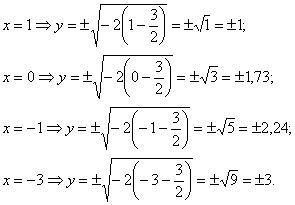
Выполним чертёж:
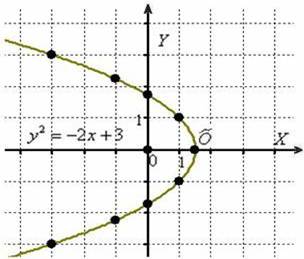
Парабола 
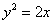


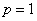

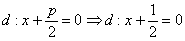
Примечание: в случае необходимости нетрудно найти координаты фокуса и уравнение директрисы неканонически расположенной параболы 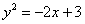

Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
Как можно отблагодарить автора?
Задачи с линиями 2-го порядка.
Как найти геометрическое место точек?
Данный практикум представляет собой логическое продолжение лекции о линиях второго порядка и её популярных представителях – эллипсе, гиперболе и параболе. Сегодня мы закрепим пройденный материал многочисленными задачами, и, кроме того, дополним теоретический багаж знаниями, которые я намеренно скрыл на первых занятиях, чтобы не перегружать «чайников» новой информацией. Признаюсь честно, ненавижу вымучивать первые абзацы своих статей (особенно, когда готов чёткий план урока), поэтому разольём кофе по чашкам, сядем в круг и перейдём к обсуждению вопросов по существу.
В самостоятельных и контрольных работах наиболее часто встречаются следующие задания:
– Найти геометрическое место точек(или составить уравнение множества точек), каждая из которых удовлетворяет определённым аналитическим условиям. Безусловно, данная формулировка является общей и не факт, что в итоге должна получиться обязательно линия, и обязательно второго порядка. Однако в контексте рассматриваемой темы эти магические слова практически всегда вызывают к жизни уравнение эллипса, окружности,гиперболы либо параболы.
– Привести уравнение линии 2-го порядка к каноническому виду. Понятие канонического вида уравнения, а также некоторые элементы этой задачи многим читателям уже знакомы, и в ближайшем будущем вам представится отличная возможность продвинуться дальше.
Нередко оба блюда подаются за один раз, то есть сначала требуется составить уравнение линии, а затем привести его к каноническому виду + в качестве десерта найти вершины, фокусы, эксцентриситет, директрисы, выполнить чертёж и т.д. Как гостеприимный хозяин заведения постараюсь всех накормить досыта, да так – чтобы некоторые не только с трудом вышли из-за стола, но и остались здесь на ночёвку =) Начислим для аппетита:
Составить уравнение линии, расстояние каждой точки которой от точки 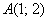

Решение данной задачи всегда начинается стандартно – в рассмотрение вводится некоторая точка 
Таким образом, наша аналитическая формулировка конкретизируется следующим образом: «составить уравнение линии, расстояние каждой точки 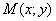
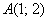

А речь здесь идёт о расстоянии 
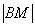
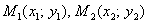
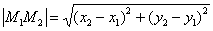
Запишем длины соответствующих отрезков:
для точек 
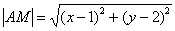
для точек 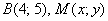

Теперь нужно составить уравнение. Согласно условию, расстояние 
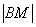
Или:
Уравнение успешно составлено, но какую линию оно задаёт – совершенно не понятно. Поэтому дальнейшие действия состоят в упрощении полученной конструкции, и сейчас мы ознакомимся с типовым техническим алгоритмом.
Во-первых, избавимся от корней. Для этого возведём в квадрат обе части:
активно пользуясь формулами сокращенного умножения, раскроем все скобки:
перенесём всё в левую часть и приведём подобные слагаемые:
разделим каждое слагаемое на –3:
Получено уравнение линии 2-го порядка в общем виде. Уже лучше, однако, и оно как неведома зверушка. По этой причине вторая часть преобразований состоит в попыткеприведения уравнения к каноническому виду. Перед нами не самый тяжёлый случай, который уже фигурировал в конце статьи о линиях второго порядка. Искусственным приёмом выделяем полные квадраты:
и завершающим штрихом рождаем квадрат в правой части:
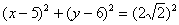


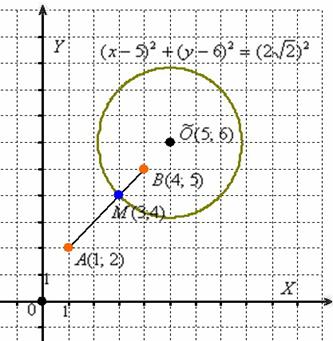
Не лишней будет кустарная, но эффективная геометрическая проверка. По условию для любой точки 

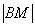


Заключительная часть задания состоит в приведении уравнения линии к каноническому виду. Центр канонической окружности должен располагаться в начале координат, и, как я неоднократно оговаривался, есть два способа разрулить ситуацию.
Первый, более простой метод:
1) Приведём уравнение окружности к каноническому виду путём её параллельного переноса центром в начало координат:
Второй, более солидный и правильный метод:
2) Осуществим параллельный перенос прямоугольной системы координат началом в точку 
Иными словами, мы перешли к новой системе координат 
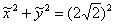
На первый взгляд кажется нелепым менять систему координат из-за одной-единственной линии, но на самом деле этот подход более корректен, и об одной простой причине его корректности я расскажу на уроке Приведение уравнения линии 2-го порядка к каноническому виду.
Ответ: искомая линия 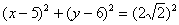


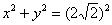
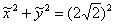
Аналогичный пример для самостоятельного решения:
Составить уравнение множества точек, для каждой из которых сумма квадратов расстояний от точек 
Краткое оформление и чертёж в конце урока.
Систематизируем порядок решения данной задачи:
На первом шаге необходимо рассмотреть точку 
На втором шаге следует найти длины нужных отрезков и в соответствии с аналитическим условием задачи составить уравнение.
На третьем шаге осуществляем упрощение полученного уравнения. Сначала приводим его к общему виду, а затем к форме, которая близА к канонической. В некоторых задачах сразу получается каноническое уравнение.
На четвёртом шаге – чертёж.
На пятом – приведение к каноническому виду.
На шестом – фокусы, асимптоты, эксцентриситет. Напоминаю, что находить их гораздо удобнее именно из канонической записи.
На практике чаще всего заданий меньше, так, в некоторых случаях не надо приводить уравнение к каноническому виду, а в самой компактной версии не требуется и чертёжа – достаточно лишь упростить уравнение и назвать линию. Я специально «нагружаю» условия задач, чтобы образцы решений годились «на все случаи жизни». Но, тем не менее, надрываться тоже не будем, и разогреемся парой новых коктейлей:
Составить уравнение множества точек, для каждой из которых квадрат расстояния до точки 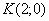
Решение: Пусть точка 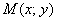
Примечание: строго говоря, в соответствии с формулировкой условия нужно рассмотреть 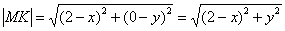
Чему равно расстояние от точки 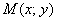
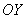
По условию 
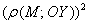
(либо 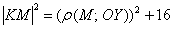
Таким образом:
Раскручиваем гайки:
«Икс квадрат» сокращается, и, очевидно, уравнение нужно максимально приблизить к каноническому виду 
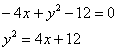

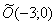

Ответ: искомое множество точек представляет собой параболу
Если дополнительно требуется привести уравнение линии к каноническому виду, то в данном примере это осуществляется элементарно:
1) Приведём уравнение параболы к каноническому виду путём её параллельного переноса центром в начало координат:
2) Перейдём к новой прямоугольной системе координат 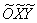
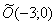
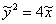
Чертёж приводить не буду, поскольку параболу 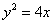
Составить уравнение множества точек, для каждой из которых расстояние до точки 
В образце решения последний пункт реализован обоими способами.
Разобранные задачи с окружностями (особенно часто), параболами встречаются и в школьной программе. Ну а на нашей тусовке 18+ становится всё жарче – снимайте джемперы и пиджаки:
Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки 


Решение: пусть точка 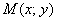
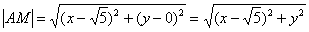
а также о расстоянии от точки до прямой, которое вычисляется по формуле 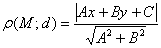
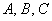
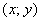
В данном случае:
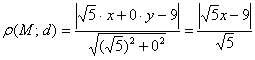
По условию для каждой точки 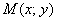



Уравнение составлено, но его вид оставляет желать лучшего. Сначала избавимся оттрёхэтажной дроби. Для этого знаменатель левой части (дробь) перекинем направо:
Сократим на 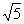
Чтобы окончательно избавиться от дробей, «поднимем тройку» на левый берег:
Дальнейшие упрощения приобретают знакомые очертания. Возводим обе части в квадрат и раскрываем скобки:
Перенесём всё налево и причешем слагаемые:
Читатели с хорошим и высоким уровнем подготовки, разумеется, могут немного видоизменять вычисления и сокращать запись, выполняя некоторые действия в уме.
Разделим обе части на 36:
Организуем трёхэтажные дроби:
И выполним деление:

Почему целесообразен именно такой алгоритм, подробно закомментировано в Примере №4 статьи о гиперболе и параболе.
В результате:
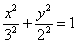

Обратите внимание, что такая формулировка однозначно определяет эллипс и добавлять что-либо излишне.
Изобразим на чертеже найденный эллипс, точку 
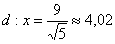
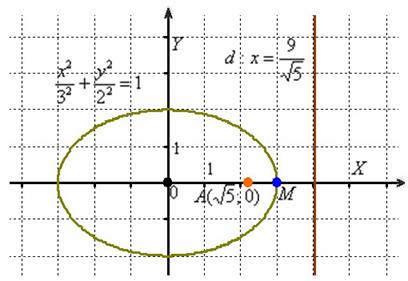
Геометрическая проверка тут затруднена, но с другой стороны и не сверхъестественна. Возьмём какую-нибудь точку эллипса, проще всего рассмотреть 
Для неё: 
По условию отношение 

Проверяем: 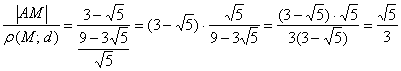
На практике можно выбрать любую точку эллипса, измерить расстояния линейкой, разделить 
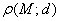
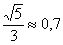
В данной задаче уравнение линии нарисовалось сразу в каноническом виде, что облегчает решение. Осталось разобраться с фокусами, эксцентриситетом, асимптотами и директрисами.
Очевидно, что у эллипса отсутствуют асимптоты.
Вычислим 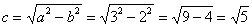

Первый фокус совпал с точкой 
Найдём эксцентриситет: 

📺 Видео
9 класс, 32 урок, Параллельный переносСкачать

§31.1 Приведение уравнения кривой к каноническому видуСкачать

Параллельный перенос вдоль оси ОХСкачать
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС И ПОВОРОТ 9 класс геометрия АтанасянСкачать

Параллельный переносСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Геометрия 9 класс (Урок№29 - Параллельный перенос.)Скачать

Движения. Симметрии. Параллельный перенос. Поворот. Урок 13. Геометрия 9 классСкачать

Геометрия и группы. Алексей Савватеев. Лекция 2.3. Параллельный переносСкачать

Параллельный перенос.Скачать

9 класс. Параллельный переносСкачать

115 Параллельный переносСкачать

параллельный перенос и поворотСкачать

115 Параллельный переносСкачать