Поворот гиперболы
Парабола
Исследование формы и расположения параболы по ее каноническому виду
Парабола со смещенной вершиной. Исследование квадратного трехчлена
Цели занятия:изучить свойства гиперболы и параболы; на примере лекции 11 найти аналогии в изучении кривых второго порядка; систематизировать знания по теме «Кривые второго порядка»; расширить школьные знания о гиперболе и параболе.
Роль и место лекции
Школьные представления о гиперболе и параболе ограничены частными случаями параболы ( 

Гипербола.
Определение 1.

Зададим в декартовой системе координат фокусы F1и F2(рис. 1). Возьмем произвольную точку M(x,y), которая по определению должна принадлежать гиперболе. Проведем отрезки F1M и F2M (рис. 1). Согласно определению рассмотрим разность этих отрезков

где 
Обозначим 


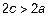




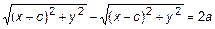
Перенесем второе слагаемое в правую часть и возведем обе части равенства в квадрат:

Раскроем скобки и сократим одинаковые члены равенства в левой и правой частях:

Возведем обе части равенства в квадрат:

Раскроем скобки и сократим одинаковые члены равенства в левой и правой частях:


Перенесем слагаемые с x и y в правую часть, остальные в левую. Вынесем за скобки x 2 и a 2 :

Отметим, что 



Выражение (3) есть уравнение гиперболы в каноническом виде.
2. Исследование формы и расположения гиперболы по ее каноническому виду

1. Так как текущие координаты входят в уравнение только в квадратах, то гипербола симметрична относительно осей начала координат. Ось симметрии, на которой находятся фокусы гиперболы, называется фокальной осью.
2. Гипербола L (3) пересекается с осями координат:
a) Пересечение с осью 


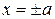




б) Пересечение с осью 


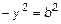






3. Из уравнения (3) найдем y :

Для I четверти выражение (4) имеет вид 


4. Крутизна. Через 





то есть с увеличением x гипербола никогда не пересечет эти прямые, при этом бесконечно приближаясь к ним. Следовательно, l1и l2 – асимптоты гиперболы.
5. Эксцентриситет гиперболы аналогичен эллипсу

Из (5) следует, что 




2.1. Частные случаи
1. Если F1 и F2 

Причем 

2. Если центр гиперболы лежит не в начале координат, а в точке 

3. Поворот гиперболы
Примем 

Повернем систему координат по часовой стрелке на угол 



С учетом 


Подставим (9) в (3). Тогда выражение гиперболы в новой системе (повернутой) координат примет вид

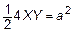


Выражение (10) есть уравнение равносторонней гиперболы, осями симметрии которой являются асимптоты.
Признаки гиперболы:
— коэффициенты при квадратах имеют противоположные знаки;
— гипербола пересекает ось координат, одноименную с переменной в квадрате, при которой коэффициент имеет знак «-»;
— в случае поворота координатных осей в уравнении кривой второго порядка (см. Лекцию 11) появляются слагаемые произведения переменных.
Определение 2.
Параболой называется геометрическое место точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
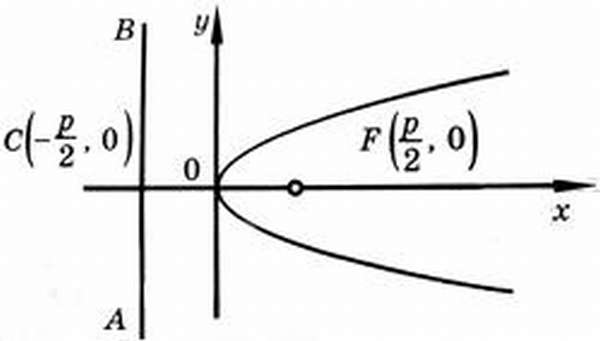
Зададим в декартовой системе координат фокус F(p/2,0)(рис. 4), где 
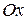







Раскроем скобки и сократим одинаковые члены
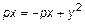


Формула (11) – каноническое уравнение параболы
5. Исследование формы и расположения параболы по ее каноническому виду
1. Характерный признак параболы: одна текущая координата в квадрате, а другая в первой степени.
2. Поскольку 

3. Найдем точки пересечения уравнения параболы с координатными осями.
Пересечение с осью 





4. 




Если F 

Вид параболы для различных уравнений


Исследование квадратного трехчлена
Задан квадратный трехчлен

Это кривая второго порядка ( 


Обозначим 




Это парабола со смещенной вершиной в точку 


Приведем это уравнение к виду (15): 



В лекции изучены понятия «гипербола» и «парабола» в общем виде, построение графиков этих функций. По общему виду уравнения второго порядка можно судить о виде кривой.
— параметры a и b в выражениях (3, 6, 7) определяют основной прямоугольник гиперболы и следовательно ее асимптоты;
— эксцентриситет гиперболы > 1;
— эксцентриситет гиперболы определяет ее вытянутость;
— при поворотах кривых второго порядка в их общих уравнениях появляются слагаемые произведения текущих переменных;
— чем меньше p, тем она более вытянута парабола, а знак p определяет направление ветвей параболы;
— степень переменной определяет ось симметрии параболы.
1. Баврин И.И. Высшая математика. – М.: Просвещение, 1980.
2. Бермант А.Ф. и др. Краткий курс математического анализа. – М.: Высшая школа, 2001.
3. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Физматлит, 2002.
4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. – М.: Наука, 1989, — 659 с.
Лекция 16

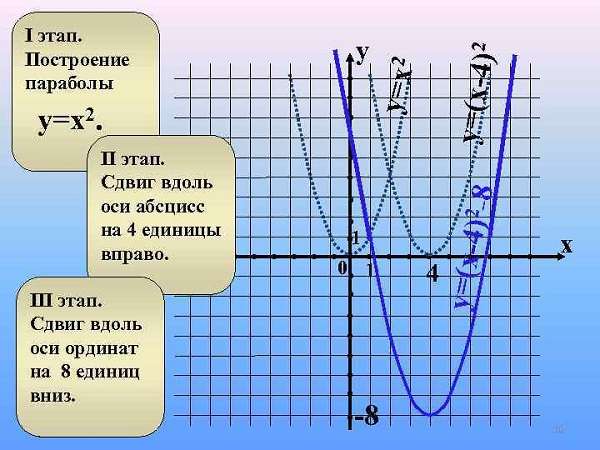
- Смещение графика квадратичной функции y = (x — b)² + c
- Презентация к уроку
- Ход урока
- 1. Организационный момент.
- 2. Исследовательская работа.
- 3. Закрепление изученного материала.
- 4. Рефлексия.
- 5. Итог урока (слайд №11):
- Парабола свойства и график квадратичной функции
- Что такое парабола и как она выглядит
- Каноническое уравнение параболы
- Свойства и график квадратичной функции
- Как определить, куда направлены ветви параболы
- Как найти вершину параболы по формуле
- Смещение параболы
- Как строить параболу по квадратному уравнению
- Директриса, эксцентриситет, фокус параболы
- Заключение
- 💥 Видео
Видео:Как определить уравнение параболы по графику?Скачать

Смещение графика квадратичной функции y = (x — b)² + c
Презентация к уроку
Загрузить презентацию (806 кБ)
Образовательная: исследовать смещение графика квадратичной функции, определить положение графика в зависимости от значений коэффициентов b, c.
Воспитательная: умение работать в группе, организованности.
Развивающая: навыки исследовательской работы, умение выдвигать гипотезы, анализировать полученные результаты, систематизировать полученные данные.
Ход урока
1. Организационный момент.
Цель урока провести исследовательскую работу. Объектом исследования будут квадратичные функции разного вида. Вам предстоит определить, как влияют коэффициенты b, c на график функций вида y=x 2 +с, y=(x-b) 2 , y=(x-b) 2 +c.
Для выполнения задания необходимо разделиться на группы (4 группы по 5 человек, одна группа “эксперты” наиболее подготовленные ученики).
Каждая группа получает план исследования , лист формата А3 для оформления результатов.
2. Исследовательская работа.
Две группы (уровень А) исследуют функции вида y= x 2 +с, одна группа (уровень В) исследует функцию вида y=(x-b) 2 , одна группа (уровень С) исследует функцию y=(x-b) 2 +c. Группа “Экспертов” исследует все функции.
| Функция | Результат | |
| 1 группа | у=x 2 +3; |  |
| 2 группа | у=x 2 -5; |  |
| 3 группа | у=(х-4) 2 ; |  |
| 4 группа | у=(х-2) 2 +3. |  |
- Для того чтобы выдвинуть гипотезу сделайте предположение, как может выглядеть ваша функция.
- Постройте график исследуемых функций (определите вершину параболы (х0, y0), задайте таблицей 4 точки).
- Сравните получившийся график с контрольным образцом y=x 2 .
- Сделайте вывод (как изменилось положение графика вашей функции относительно контрольного образца).
- Результаты оформите на листе формата А3 и представьте “экспертной” группе.
“Экспертная” группа сверяет результаты свои с результатами остальных групп, систематизирует и обобщает результаты, выступает с выводами. В случае неточностей или ошибок учитель вносит коррекционные замечания.
Сверка полученных результатов со слайдами №2-5.
Любую квадратичную функцию y=ax 2 +bx+c, можно записать в виде y=a(x-x0) 2 +y0, где x0 и y0 выражаются через коэффициенты a, b, c. Таким образом, ваши коэффициенты b=x0, c=y0 являются координатами вершины параболы.
3. Закрепление изученного материала.
Фронтальная работа с классом.
1. Найти ошибку в графиках функций (Слайды№6-9).
y=(х+6) 2
у=х 2 -2
Коэффициент b
Нет ошибки
Рисунок 1
Рисунок 2




Какой коэффициент вам помог найти ошибку?
2. Соотнесите графики функций согласно цветам (слайд №10).
| y=(х-4) 2 -2 | синий |
| y=-x 2 +5 | красный |
| y=(x+1) 2 +3 | зеленый |
| y=(x-3) 2 | фиолетовый |
4. Рефлексия.
Группа “Экспертов” отвечают на вопросы:
– Какие ошибки допустили группы?
– Достигнута ли цель занятия?
– Соответствуют ли полученные результаты исследования поставленной гипотезе?
5. Итог урока (слайд №11):
На положение графика функции y=(x-b) 2 +c влияют коэффициенты b и c,
“+b” парабола сдвинута вправо по оси абсцисс на b единичных отрезков,
“–b” парабола сдвинута влево по оси абсцисс на b единичных отрезков,
“+с” парабола сдвинута вверх по оси ординат на с единичных отрезков,
“-с” парабола сдвинута вниз по оси ординат на с единичных отрезков.
Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Парабола свойства и график квадратичной функции
Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.
Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.
Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.
Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.
Видео:Как легко составить уравнение параболы из графикаСкачать

Что такое парабола и как она выглядит
Алгебра: под этим термином понимается график квадратичной функции.
Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:
- Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).
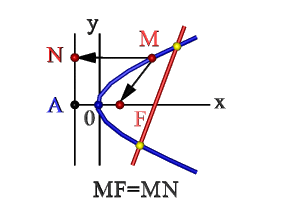
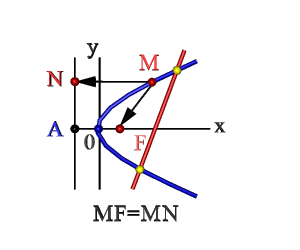
- Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.
Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Каноническое уравнение параболы
На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.
Каноническое уравнение имеет вид:
где коэффициент p – фокальный параметр параболы (AF).
В алгебре оно запишется иначе:
y = a x2 + b x + c (узнаваемый шаблон: y = x2).
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Свойства и график квадратичной функции
Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.
Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.
Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

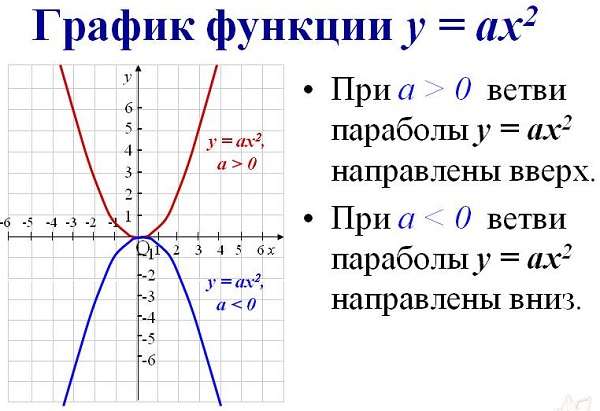
Как определить, куда направлены ветви параболы
Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.
Видео:Как строить параболу со смещенной вершиной. График функции y=(x-m)2+n. График y=x2+bx+cСкачать

Как найти вершину параболы по формуле
Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.
Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.
Формулы нахождения вершины:
Пример.
Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.
Для такой линии:
- х = -16 / (2 * 4) = -2,
- y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.
Получаем координаты вершины (-2, -41).
Видео:Уравнение параболы #алгебра #графики #парабола #репетиторСкачать

Смещение параболы
Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).
Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.
Пример.
Имеем: b = 2, c = 3.
Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.
Видео:Графики как задать уравнение параболыСкачать

Как строить параболу по квадратному уравнению
Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.
Анализируя выражения и уравнения, можно увидеть следующее:
- Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.
- Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.
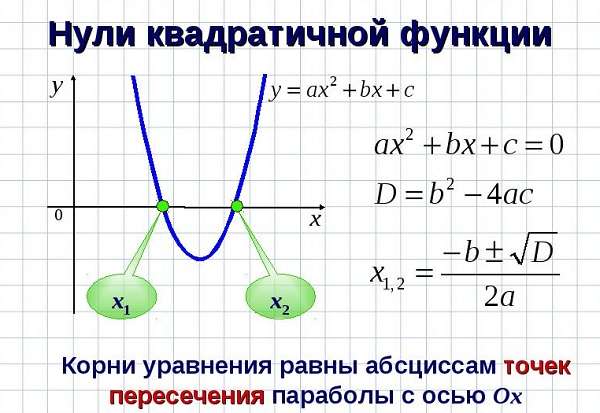
Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:
Для этого нужно приравнять выражение к нулю.
Наличие корней параболы зависит от результата:
- D ˃ 0, то х1, 2 = (-b ± D0,5) / (2 * a),
- D = 0, то х1, 2 = -b / (2 * a),
- D ˂ 0, то нет точек пересечения с вектором ОХ.
Получаем алгоритм построения параболы:
- определить направление ветвей,
- найти координаты вершины,
- найти пересечение с осью ординат,
- найти пересечение с осью абсцисс.
Пример 1.
Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:
- а = 1, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-5) / 2 = 5/2, y = (5/2)2 — 5 * (5/2) + 4 = -15/4,
- с осью ординат пересекается в значении у = 4,
- найдем дискриминант: D = 25 — 16 = 9,
- ищем корни:
- Х1 = (5 + 3) / 2 = 4, (4, 0),
- Х2 = (5 — 3) / 2 = 1, (1, 0).
По полученным точкам можно построить параболу.
Пример 2.
Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:
- а = 3, следовательно, ветви направлены вверх,
- координаты экстремума: х = (-2) / 2 * 3 = 1/3, y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3,
- с осью у будет пересекаться в значении у = -1,
- найдем дискриминант: D = 4 + 12 = 16. Значит корни:
- Х1 = (2 + 4) / 6 = 1, (1,0),
- Х2 = (2 — 4) / 6 = -1/3, (-1/3, 0).
По полученным точкам можно построить параболу.
Видео:§24 Каноническое уравнение параболыСкачать

Директриса, эксцентриситет, фокус параболы
Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).
Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.
Эксцентриситет (константа) = 1.
Видео:Как написать уравнение параболы с помощью графикаСкачать

Заключение
Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.
💥 Видео
Как думать в математике. Вершина параболы для чайников. #математика #алгебра #парабола #думатьСкачать

Как найти вершину параболы?Скачать

Квадратичная функция и ее график. 8 класс.Скачать

213. Фокус и директриса параболы.Скачать

Как строить параболу? | TutorOnlineСкачать

Вершина параболы и ось симметрии. ПримерСкачать

Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

Как найти все коэффициенты параболы по графику? Большой ответ на этот вопрос.Скачать

Видеоурок "Парабола"Скачать