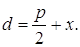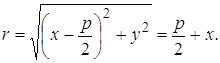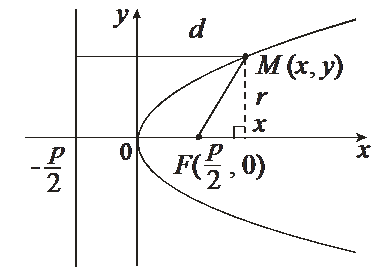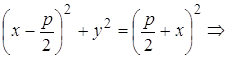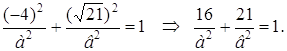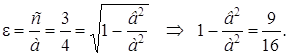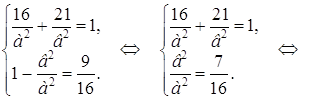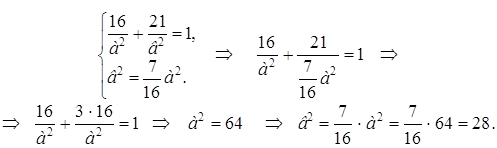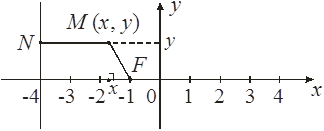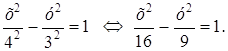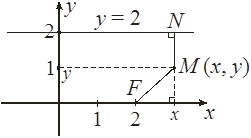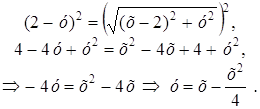Видео:Вершина параболы и ось симметрии. ПримерСкачать
Глава 20. Парабола
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.
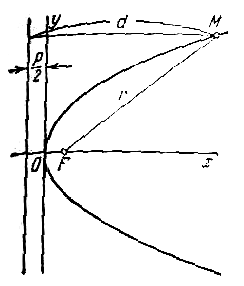
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением
(1)
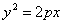
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение
.
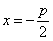
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле
.
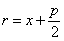
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид
(2)
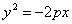
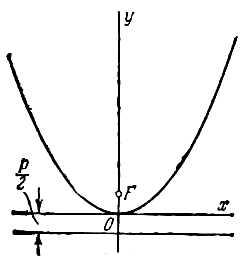
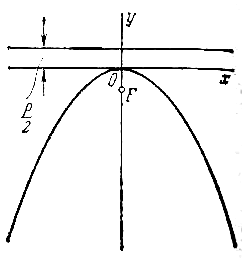
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение
(3)
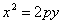
если она лежит в верхней полуплоскости (рис.), и
(4)
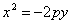
если в нижней полуплоскости (рис.)
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.
Видео:КАК СТРОИТЬ ПАРАБОЛУ. ОСЬ СИММЕТРИИ (Финальная часть саги о функциях)Скачать
2.5 Парабола
Парабола Есть геометрическое место точек на плоскости, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Выберем систему координат таким образом (рисунок 2.7): за ось ОХ примем прямую, проходящую через фокус F перпендикулярно к директрисе, за положительное направление примем направление от директрисы к фокусу. За начало координат примем середину О отрезка от точки F до директрисы, длину которого обозначим через Р и будем называть параметром параболы. Пусть М(Х, У) произвольная точка, лежащая на параболе. Пусть точка N основание перпендикуляра, опущенного из М На директрису. По определению параболы MN = MF.
Из этого условия получаем Каноническое уравнение параболы в выбранной системе координат
Пусть P > 0, исследуем форму параболы.
Из канонического уравнения параболы видно, что Х не может принимать отрицательных значений, т. е. все точки параболы лежат справа от оси ОY. Уравнение содержит переменную У В квадрате, значит парабола симметрична относительно оси ОХ, эта ось называется Осью Параболы. Точка О пересечения параболы с ее осью симметрии называется Вершиной параболы.
Для параболы, заданной уравнением (2.11), вершина совпадает с началом координат, а ось симметрии – с осью ОХ. График параболы имеет вид, изображенный на рисунке 2.7. Уравнение директрисы записывается в виде 
.
Фокус параболы для параболы с осью симметрии – осью Х имеет вид F(
,0), а для параболы с осью симметрии осью Y – F(0,).
Определяет параболу, область определения которой 
.
Имеет вершину в начале координат, фокус 
, директрису 
; ветви параболы направлены в положительную сторону оси OY и ветви направлены в отрицательную сторону оси OY, если уравнение параболы Х2 = –2Py. Осью симметрии такой параболы является ось ОY, а вершиной – начало координат.
Пример 2.4. Составить уравнение параболы и ее директрисы, зная, что она симметрична относительно оси ОY, фокус находится в точке F(0; 2), вершина совпадает с началом координат.
Решение. Будем искать уравнение параболы в виде Х2 = 2Py, так как по условию она симметрична относительно оси OY.
По условию 
, а значит, P = 4. Итак, искомое уравнение имеет вид Х2 = 8У, уравнение ее директрисы у = –2.
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать
Парабола
Параболой называется множество точек плоскости, равноудаленных от данной точки F этой плоскости, называемой фокусом параболы, и данной прямой, называемой ее директрисой.
Построим уравнение параболы.
Пусть ось Оx проходит через фокус F параболы и перпендикулярен директрисе, а ось Оу проходит посередине между фокусом и директрисой. Обозначим через p – расстояние между фокусом и директрисой. Тогда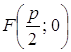 
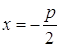
, а уравнение директрисы 
.
Число p – называется фокальным параметром параболы.
Пусть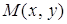 
– произвольная точка параболы. Пусть 
– фокальный радиус точки M. d – расстояние от точки М до директрисы. Тогда 
По определению параболы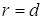 
. Следовательно
Возведем это уравнение в квадрат
(20)
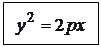
– каноническое уравнение параболы, симметричной относительно оси Оx и проходящей через начало координат.
Точка (0; 0) – вершина параболы.
Если р > 0 (р > 0 ), то парабола (20) расположена правее (левее) оси Оу.
Так как для параболы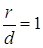 
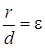
, а для эллипса и гиперболы 
, то, следовательно, эксцентриситет параболы равен 1 (e = 1).
Заметим, что парабола, симметричная относительно Оу и проходящая через начало координат, определяется уравнением
Фокус этой параболы находится в точке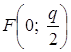 
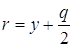
. Уравнение ее директрисы 
. Фокальный радиус ее точки М(х, у) выражается формулой 
.
Если q > 0 (q 2 + у 2 – 4х + 6у – 3 = 0.
Выделим полные квадраты в данном уравнении:
х 2 + у 2 – 4х + 6у – 3 = (х 2 – 4х + 4) – 4 + (у 2 + 6у + 9) – 9 – 3 = 0
Þ (х – 2) 2 + (у + 3) 2 = 16.
Учитывая уравнение окружности (1), имеем, что ее центр находится в точке с координатами (2; –3), а радиус равен 4.
Эллипс, симметричный относительно осей координат, фокусы которого находятся на оси Ох, проходит через точку М(–4;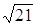 
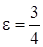
) и имеет эксцентриситет 
. Написать уравнение эллипса и найти фокальные радиусы точки М.
Каноническое уравнение эллипса имеет вид 
Так как эллипс проходит через точку М, то ее координаты должны удовлетворять этому уравнению
Фокусы находятся на оси Ох, следовательно
Объединив полученные два уравнения в систему, найдем а 2 и в 2 :
Следовательно, уравнение данного эллипса имеет вид:
Фокальные радиусы точки М определим по формулам (8): х = –4, 
, .
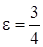
Þ r1 = а + eх =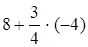 
= 8 – 3 = 5,
r2 = а – eх =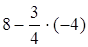 
= 8 + 3 = 11.
Определить траекторию точки М, которая при своем движении остается вдвое ближе к точке F (–1; 0), чем к прямой х = –4.
Пусть М (х, у). Тогда çMNú = 2 çMFú, çMNú = ç–4 – xú, çMFú= =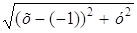 
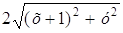
, Þ ç– (4 + х)ú = 
.
Возведем в квадрат: (4 + х) 2 = 4 ((х + 1) 2 + у 2 ),
Þ 16 + 8х + х 2 = (х 2 + 2х + 1 + у 2 ) · 4 = 4х 2 + 8х + 4 + 4у 2 ,
Þ 3х 2 + 4у 2 = 12 Þ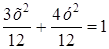 
Þ 
.
Таким образом, точка М (х, у) движется по эллипсу.
Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса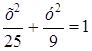 
.
Из уравнения данного эллипса имеем: а = 5; в = 3, а > в.
Следовательно,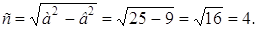 
Поэтому, вершинами эллипса будут точки (±5; 0), (0; ±3), а фокусами точки F1(–с; 0) = (–4; 0), F2(4; 0).
Так как фокусы эллипса находятся на оси Ох (а > в), то вершины (±5; 0) будут фокусами гиперболы. Каноническое уравнение гиперболы, имеющей фокусы на оси Ох, имеет вид (13)
,
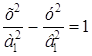
причем F1(–5; 0), F2(5; 0) – фокусы данной гиперболы, т. е. с1 = 5. Найдем а1 и в1.
Так как вершины данной гиперболы находятся в фокусах эллипса, то а1 = с = 4. Следовательно:
.
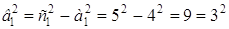
Таким образом, уравнение гиперболы имеет вид
Составить уравнение геометрического места точек, одинаково удаленных от точки F(2; 0) и от прямой у = 2. Найти вершину параболы, точки пересечения ее с осью Ох.
Пусть точка М (х, у) – принадлежит данному множеству точек.
Следовательно çFMú = çNMú , çFMú == 
, çNMú = 2 – у, Þ 2 – у = 
.
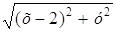
Возведем в квадрат:
– парабола, ветви которой направлены вниз.
Найдем точки пересечения данной параболы с осью Ох.
у = 0 Þ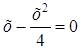 
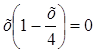
Þ 
Þ х1 = 0; х2 = 4.
Т. е. это будут точки (0; 0); (4; 0).
Þ Вершина параболы будет в точке с абсциссой х = 2 Þ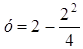 
= = 2 – 1 = 1, т. е.
Вершиной параболы будет точка (2; 1).
На параболе у 2 = 6х найти точку, фокальный радиус которой равен 4,5.
Так как у 2 = 2рх Þ 2р = 6, р = 3.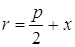 
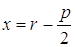
Þ 
= = 
Значит у 2 = 6 · 3 = 18 Þ у = ± 
= ±
. Þ (3; ±) – две таких точки.
1. Гусак А. А. Аналитическая геометрия и линейная алгебра.– Мн.: Тетрасистемс, 1998.
2. Овсеец М. И., Светлая Е. М. Сборник задач по высшей математике. Учебное издание.– Мн.: ЧИУиП, 2006.– 67 с.
💥 Видео
ГРАФИК ФУНКЦИЙ — Сдвиги Графика Функции, Как строить Графики Функции // Алгебра 8 классСкачать
ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать
Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать
Как легко составить уравнение параболы из графикаСкачать
Геометрические преобразования графиков функций. Растяжение, сжатие и симметрия относительно оси ОХСкачать
Преобразования графиков функций. Урок 13. Симметрия относительно оси ординат.Скачать
Как определить уравнение параболы по графику?Скачать
Преобразование графиков функций. y= f(x) + n. Сдвиг по оси OY. 10 класс.Скачать
КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать
Симметрия относительно прямойСкачать
Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать
Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать
Вариант 72, № 5. Уравнение оси симметрии параболы. Пример 2Скачать
Преобразование графиков функций. Сжатие и растяжение. 10 класс.Скачать
§24 Каноническое уравнение параболыСкачать
Симметричные отображения графиков относительно осей координатСкачать
Преобразование графиков функций. y= f(x + n). Сдвиг по оси OX. 10 класс.Скачать
