Уравнение параболы с вершиной в точке 1 3 проходящей через

Видео:Как легко составить уравнение параболы из графикаСкачать

Как определить a, b и c по графику параболы

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

Видео:Как определить уравнение параболы по графику?Скачать

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент (a) можно найти с помощью следующих фактов:

— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

Решаем систему.
Пример:

Вычтем из второго уравнения первое:

Подставим (9a) вместо (b):

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение (a):

Получается квадратичная функция: (y=-x^2-9x-15).

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

Сложим 2 уравнения:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.

График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

Видео:№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать

Уравнение параболы с вершиной в точке ( — 1 ; — 3), проходящей через точку (1 ; 1), имеет вид?

Алгебра | 5 — 9 классы

Уравнение параболы с вершиной в точке ( — 1 ; — 3), проходящей через точку (1 ; 1), имеет вид.

Составим систему уравнений с тремя неизвестными по имеющимся координатам вершины и одной точки на параболе :

Сначала выведу b и c через a : $left < << frac=-1> atop > right. = textgreater left < <atop > right. = textgreater left < <atop > right.$

Найду a : $a+b+c=1 \ a+2a+a-3=1 \ 4a=4 \ a=1$

Тогда b = 2a = 2, а c = a — 3 = — 2

Ответ : уравнение параболы : y = x² + 2x — 2.

Видео:Как найти вершину параболы?Скачать

Напишите уравнение параболы у = kx ^ 2, проходящей через точку K( — 2 ; — 20)?

Напишите уравнение параболы у = kx ^ 2, проходящей через точку K( — 2 ; — 20).

Видео:Вершина параболы и ось симметрии. ПримерСкачать

Уравнение прямой, проходящей через точки A(1 ; — 5) B( — 4 ; — 2) имеет вид ?

Уравнение прямой, проходящей через точки A(1 ; — 5) B( — 4 ; — 2) имеет вид :

Видео:Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

Напишите уравнение прямой, проходящей через точки пересечения парабол и?

Напишите уравнение прямой, проходящей через точки пересечения парабол и.

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

График квадратичной функции — парабола с вершиной в точке А(0 ; — 3), проходящий через точку В(3 ; 24) Задать эту функцию формулой?

График квадратичной функции — парабола с вершиной в точке А(0 ; — 3), проходящий через точку В(3 ; 24) Задать эту функцию формулой!

Видео:Построение параболыСкачать

Ордината вершины параболы y = — x в квадрате + ax + 5 проходящей через точку (2 ; 5) равна?

Ордината вершины параболы y = — x в квадрате + ax + 5 проходящей через точку (2 ; 5) равна.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Задайте формулой квадратичную функцию график которой парабола с вершиной в точке (1 ; 11), проходящей через точку (0 ; 10)?

Задайте формулой квадратичную функцию график которой парабола с вершиной в точке (1 ; 11), проходящей через точку (0 ; 10).

Видео:213. Фокус и директриса параболы.Скачать

Уравнение прямой, проходящей через точки А( — 3 ; 1) и В( — 5 ; 9), имеет вид?

Уравнение прямой, проходящей через точки А( — 3 ; 1) и В( — 5 ; 9), имеет вид.

Видео:Составляем уравнение прямой по точкамСкачать

Составить уравнение параболы, проходящей через точки (0 ; 0) и точку (2 ; — 4) симметрично оси Oy?

Составить уравнение параболы, проходящей через точки (0 ; 0) и точку (2 ; — 4) симметрично оси Oy.

Видео:Вычисляем высоту через координаты вершин 1Скачать

Составить уравнение параболы, проходящей через точки (0 ; 0) и точку ( — 1 ; — 3) симметрично оси Ox?

Составить уравнение параболы, проходящей через точки (0 ; 0) и точку ( — 1 ; — 3) симметрично оси Ox.

Видео:Уравнения стороны треугольника и медианыСкачать

Общее уравнение прямой, проходящей через точки А( — 2, 3) и В(2, — 3) имеет вид?

Общее уравнение прямой, проходящей через точки А( — 2, 3) и В(2, — 3) имеет вид.

Вы зашли на страницу вопроса Уравнение параболы с вершиной в точке ( — 1 ; — 3), проходящей через точку (1 ; 1), имеет вид?, который относится к категории Алгебра. По уровню сложности вопрос соответствует учебной программе для учащихся 5 — 9 классов. В этой же категории вы найдете ответ и на другие, похожие вопросы по теме, найти который можно с помощью автоматической системы «умный поиск». Интересную информацию можно найти в комментариях-ответах пользователей, с которыми есть обратная связь для обсуждения темы. Если предложенные варианты ответов не удовлетворяют, создайте свой вариант запроса в верхней строке.

Видео:Как найти уравнение параболы Найти коэффициент а через точки ОГЭ математика задание 5Скачать

Уравнение параболы с вершиной в точке 1 3 проходящей через

Видео:10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Глава 20. Парабола

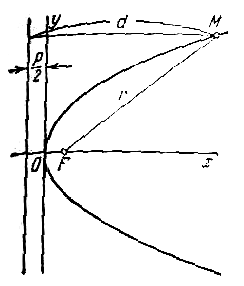
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением

(1)

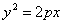
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

.

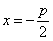
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле

.

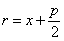
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид

(2)

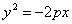
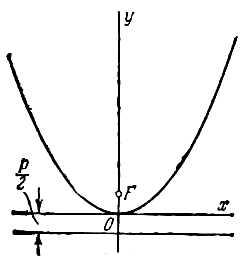
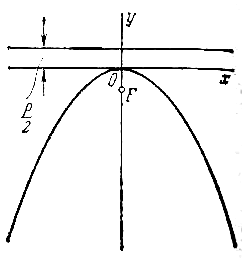
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение

(3)

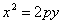
если она лежит в верхней полуплоскости (рис.), и

(4)

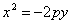
если в нижней полуплоскости (рис.)

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.

🌟 Видео

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Как найти все коэффициенты параболы по графику? Большой ответ на этот вопрос.Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Урок 100. Квадратичная функция и ее свойства (8 класс)Скачать