Парабола Есть геометрическое место точек на плоскости, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
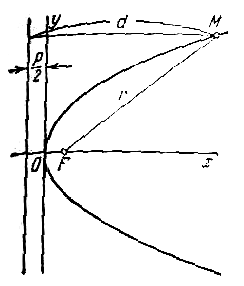
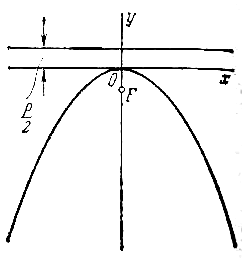
Выберем систему координат таким образом (рисунок 2.7): за ось ОХ примем прямую, проходящую через фокус F перпендикулярно к директрисе, за положительное направление примем направление от директрисы к фокусу. За начало координат примем середину О отрезка от точки F до директрисы, длину которого обозначим через Р и будем называть параметром параболы. Пусть М(Х, У) произвольная точка, лежащая на параболе. Пусть точка N основание перпендикуляра, опущенного из М На директрису. По определению параболы MN = MF.
Из этого условия получаем Каноническое уравнение параболы в выбранной системе координат
Пусть P > 0, исследуем форму параболы.
Из канонического уравнения параболы видно, что Х не может принимать отрицательных значений, т. е. все точки параболы лежат справа от оси ОY. Уравнение содержит переменную У В квадрате, значит парабола симметрична относительно оси ОХ, эта ось называется Осью Параболы. Точка О пересечения параболы с ее осью симметрии называется Вершиной параболы.
Для параболы, заданной уравнением (2.11), вершина совпадает с началом координат, а ось симметрии – с осью ОХ. График параболы имеет вид, изображенный на рисунке 2.7. Уравнение директрисы записывается в виде 
Фокус параболы для параболы с осью симметрии – осью Х имеет вид F(

Определяет параболу, область определения которой 
Имеет вершину в начале координат, фокус 

Пример 2.4. Составить уравнение параболы и ее директрисы, зная, что она симметрична относительно оси ОY, фокус находится в точке F(0; 2), вершина совпадает с началом координат.
Решение. Будем искать уравнение параболы в виде Х2 = 2Py, так как по условию она симметрична относительно оси OY.
По условию 
- Квадратичная функция. Построение параболы
- Основные понятия
- Построение квадратичной функции
- Алгоритм построения параболы
- Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
- Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
- Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
- Уравнение параболы с вершиной в начале координат и ветви которой направлены вправо имеет вид
- Глава 20. Парабола
- 📸 Видео
Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Квадратичная функция. Построение параболы
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Видео:Как легко составить уравнение параболы из графикаСкачать

Основные понятия
Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию означает определить правило, в соответствии с которым каждому значению аргумента соответствует единственное значение функции. Вот какими способами ее можно задать:
- Табличный способ. Помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ: наглядно.
- Аналитический способ, через формулы. Компактно и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек координатной плоскости, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.
Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.
Видео:КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать

Построение квадратичной функции
Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0.
График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 в частном случае при b = 0, c = 0:
Точки, обозначенные фиолетовыми кружками, называют базовыми точками. Чтобы найти их координаты для функции y = x 2 , нужно составить таблицу:
x
y
Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов. При увеличении старшего коэффициента график сужается, при уменьшении — расширяется.
График функции y = –x 2 выглядит, как перевернутая парабола:
Зафиксируем координаты базовых точек в таблице:
x
y
Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:
- Если старший коэффициент больше нуля (a > 0), то ветви параболы напрaвлены вверх.
- Если старший коэффициент меньше нуля (a 2 + bx + c. Чтобы найти точки пересечения с осью Ox, нужно решить квадратное уравнение ax 2 + bx + c = 0. В процессе найдем дискриминант D = b 2 — 4ac, который даст нам информацию о количестве корней квадратного уравнения.
Рассмотрим три случая:
- Если D 0,то график выглядит так:
- Если D = 0, то уравнение имеет одно решение, а парабола пересекает ось ОХ в одной точке. Если a > 0, то график имеет такой вид:
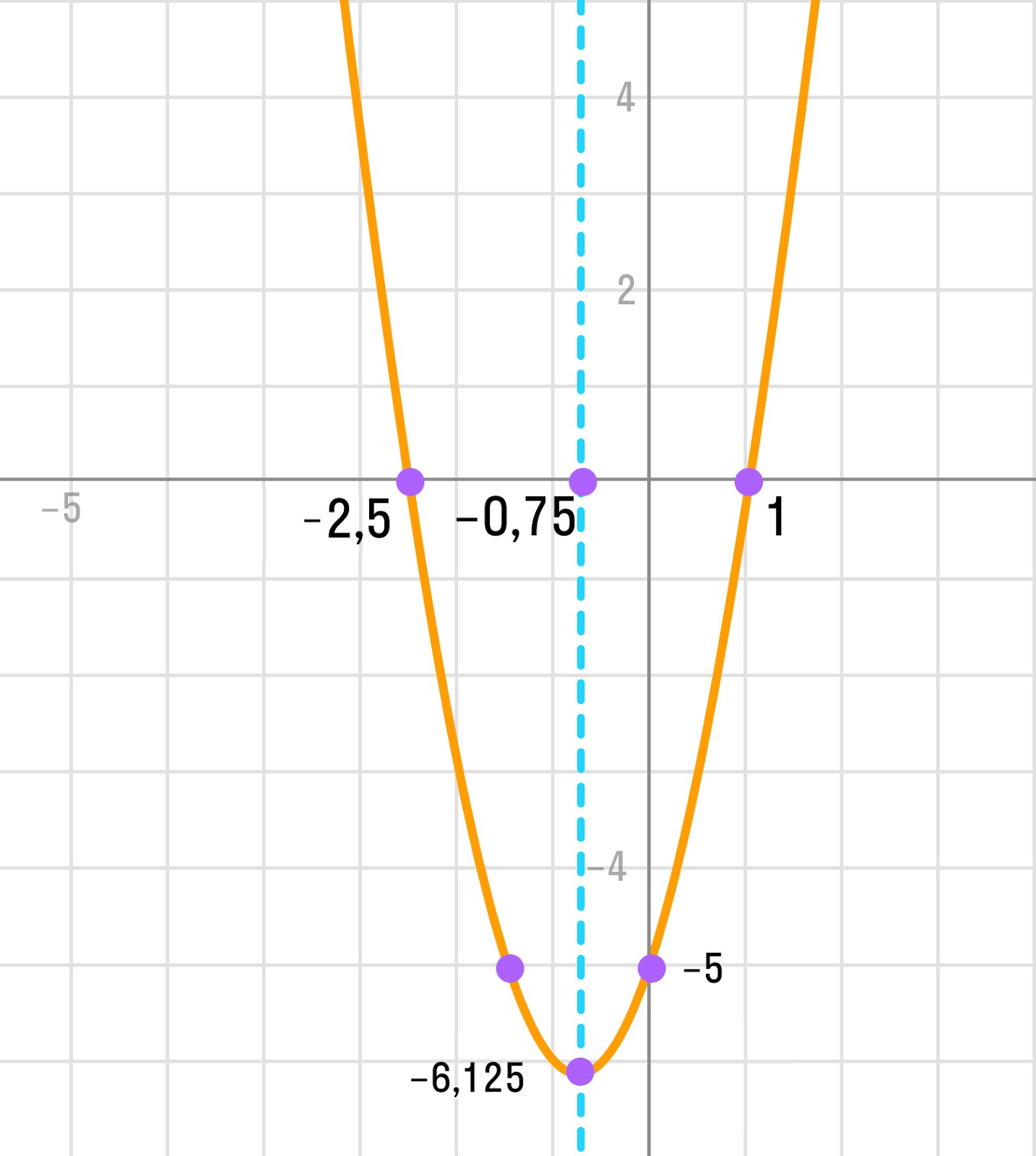
- Если D > 0, то уравнение имеет два решения, а парабола пересекает ось ОХ в двух точках, которые можно найти следующим образом:
Если a > 0, то график выглядит как-то так:
0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>
Теперь понятно, что, зная направление ветвей параболы и знак дискриминанта, мы можем схематично представить график конкретной функции.
Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:
Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.
Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).
На изображении отмечены основные параметры графика квадратичной функции:
Видео:ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график ПараболаСкачать

Алгоритм построения параболы
Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.
Видео:Парабола. Квадратичная функцияСкачать

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.
Разберем общий алгоритм на примере y = 2x 2 + 3x — 5.
Как строим:
- Определим направление ветвей параболы. Так как а = 2 > 0, ветви параболы направлены вверх.
- Найдем дискриминант квадратного трехчлена 2x 2 + 3x — 5.
D = b 2 — 4ac = 9 — 4 * 2 * (-5) = 49 > 0
В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:
Точка пересечения с осью OY находится: (0; -5) относительно оси симметрии.
Нанесем эти точки на координатную плоскость и построим график параболы:
Видео:Построение параболыСкачать

Уравнение квадратичной функции имеет вид y = a * (x — x₀) 2 + y₀
Зная координаты вершины параболы и старший коэффициент, можно записать уравнение квадратичной функции в виде у = a(x − x0) + y0, где x0, y0 — координаты вершины параболы.
Координаты его вершины: (x₀; y₀). В уравнении квадратичной функции y = 2x 2 + 3x — 5 при а = 1, то второй коэффициент является четным числом.
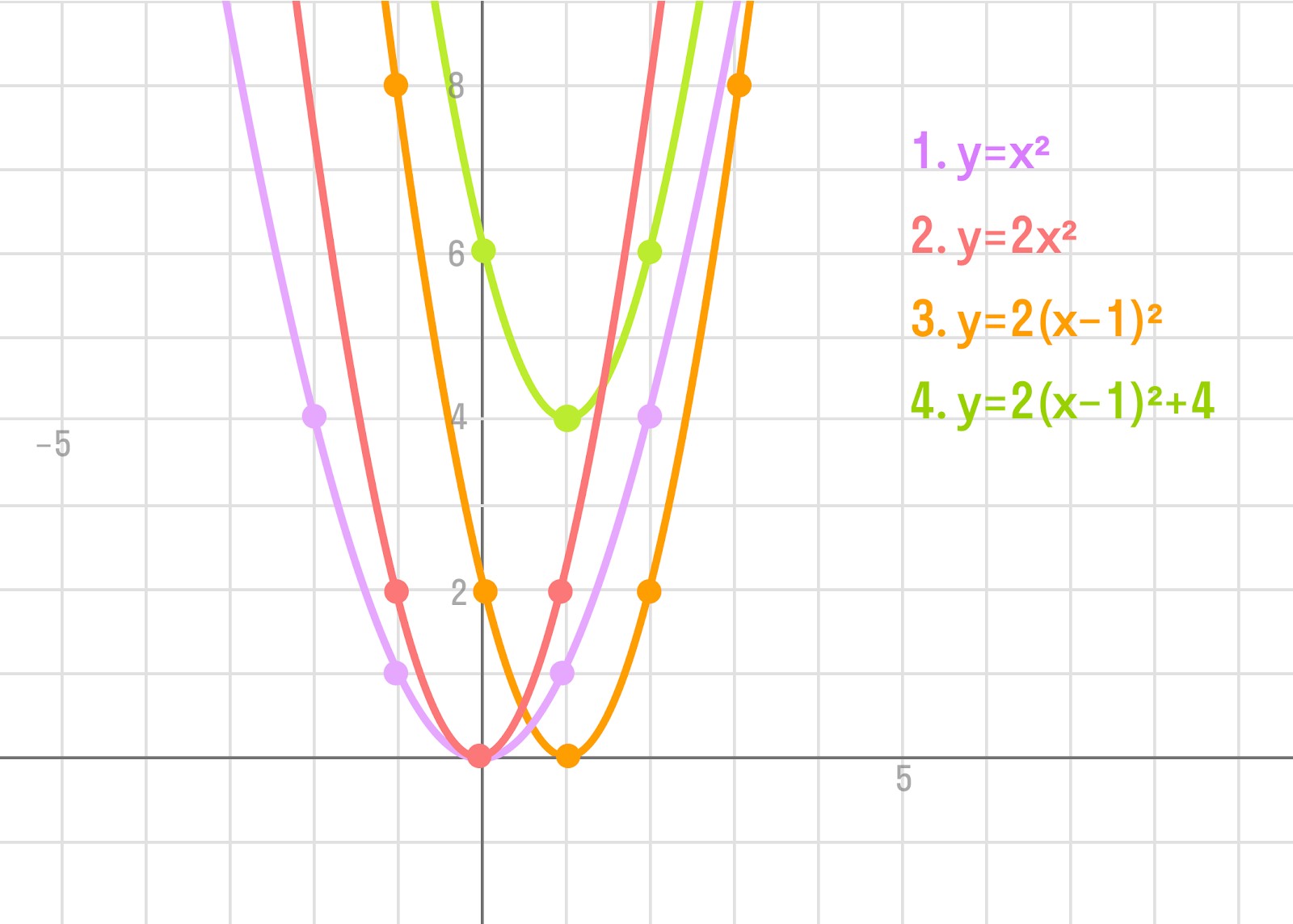
Рассмотрим пример: y = 2 * (x — 1) 2 + 4.
Как строим:
- Воспользуемся линейным преобразованием графиков функций. Для этого понадобится:
- построить график функции y = x 2 ,
- умножить ординаты всех точек графика на 2,
- сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- сдвинуть его вдоль оси OY на 4 единицы вверх.
Построить график параболы для каждого случая.
Видео:Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)
Рассмотрим следующий пример: y = (x − 2) × (x + 1).
Как строим:
Данный вид функции позволяет быстро найти нули функции:
(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.
Определим координаты вершины параболы:
Найти точку пересечения с осью OY:
с = ab = (−2) × (1) = −2 и ей симметричная относительно оси симметрии параболы.
Отметим эти точки на координатной плоскости и соединим плавной прямой линией.
Видео:Квадратичная функция. Вершина параболы и нули функции. 8 класс.Скачать

Уравнение параболы с вершиной в начале координат и ветви которой направлены вправо имеет вид
Видео:§24 Каноническое уравнение параболыСкачать

Глава 20. Парабола
Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой. Фокус параболы обозначается буквой F , расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.
Пусть дана некоторая парабола. Введем декартову прямоугольную систему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посередине между фокусом и директрисой (рис.). В этой системе координат данная парабола будет определяться уравнением
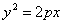
Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение
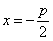
Фокальный радиус произвольной точки М( x; y ) параболы (то есть длина отрезка F(M ) может быть вычислен по формуле
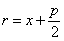
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка пересечения параболы с осью называется ее вершиной. При указанном выше выборе координатной системы ось параолы совмещена с осью абсцисс, вершина находится в начале координат, вся парабола лежит в правой полуплоскости.
Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в левой полуплоскости (рис.), то ее уравнение будет иметь вид
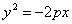
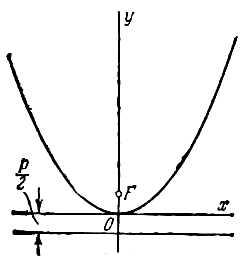
В случае, когда начало координат находится в вершине, а с осью совмещена ось ординат, парабола будет иметь уравнение
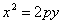
если она лежит в верхней полуплоскости (рис.), и
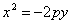
если в нижней полуплоскости (рис.)
Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), называется каноническим.
📸 Видео
213. Фокус и директриса параболы.Скачать

Урок 100. Квадратичная функция и ее свойства (8 класс)Скачать

Парабола (часть 1). Каноническое уравнение параболы. Высшая математика.Скачать

Как найти вершину параболы?Скачать

Видеоурок "Парабола"Скачать

Графики №11. Парабола(ОГЭ)Скачать

Квадратичная функция и ее график. 8 класс.Скачать

Вершина параболы и ось симметрии. ПримерСкачать

Как строить параболу? | TutorOnlineСкачать

Как определить уравнение параболы по графику?Скачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать