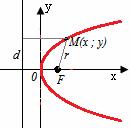
Уравнение параболы по директрисе онлайн (8 видео)

Парабола

Элементы параболы
0F — фокальная ось
0 — вершина
— фокус
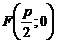
ε=1 — эксцентриситет
— фокальный радиус
— директриса
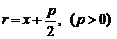
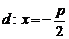
p — фокальный параметр

Каноническое уравнение параболы (ось Ox совпадает с фокальной осью, начало координат – с вершиной параболы): y 2 =2px
При p x 2 =2py
При p>0 ветви параболы направлены вверх, при p 2 /2+(y-1) 2 /2=1, необходимо набрать в поле x^2/2+(y-1)^2/2=1 и нажать кнопку График параболы .

Самостоятельно построить график можно, используя операцию выделения полного квадрата.

Содержание

Решение задач по математике онлайн
Калькулятор онлайн. Построение графика квадратичной функции.
Парабола: формулы, примеры решения задач
📹 Видео

Видео:Как определить уравнение параболы по графику?Скачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Как легко составить уравнение параболы из графикаСкачать

Калькулятор онлайн.
Построение графика квадратичной функции.

Если вам нужно просто построить график любой функции, то для этого у нас есть отдельная программа.

Эта математическая программа для построения графика квадратичной функции сначала делает преобразование вида
( y=ax^2+cx+b ;; rightarrow ;; y=a(x+p)^2+q )
а затем последовательно строит графики функций:
$$ y=ax^2 $$
$$ y=a(x+p)^2+q $$

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода квадратного многочлена, рекомендуем с ними ознакомиться.

В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.

Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.

Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x — 3,5x^2

Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.

Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 — 5&6/5x +1/7x^2
Результат: ( 3frac — 5frac x + fracx^2 )

При вводе выражения можно использовать скобки. В этом случае при решении введённое выражение сначала упрощается.
Например: 1/2(x-1)(x+1)-(5x-10&1/2)

Видео:Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать

Парабола: формулы, примеры решения задач

Определение параболы. Параболой называется множество всех точек плоскости, таких, каждая из которых находится на одинаковом расстоянии от точки, называемой фокусом, и от прямой, называемой директрисой и не проходящей через фокус.

Каноническое уравнение параболы имеет вид:

где число p, называемое параметром параболы, есть расстояние от фокуса до директрисы.

На чертеже линия параболы — бордового цвета, директриса — ярко-красного цвета, расстояния от точки до фокуса и директрисы — оранжевого.

В математическом анализе принята другая запись уравнения параболы:

то есть ось параболы выбрана за ось координат. Можно заметить, что ax² — это квадратный трёхчлен ax² + bx + c , в котором b = 0 и c = 0 . График любого квадратного трёхчлена, то есть левой части квадратного уравнения, будет параболой.

Фокус параболы имеет координаты

Директриса параболы определяется уравнением .

Расстояние r от любой точки параболы до фокуса определяется формулой .

Для каждой из точек параболы расстояние до фокуса равно расстоянию до директрисы.

Пример 1. Определить координаты фокуса параболы

Решение. Число p расстояние от фокуса параболы до её директрисы. Начало координат в данном случае — в роли любой точки, расстояния от которой от фокуса до директрисы равны. Находим p:

Находим координаты фокуса параболы:

Пример 2. Составить уравнение директрисы параболы

Решение. Находим p:

Получаем уравнение директрисы параболы:

Пример 3. Составить уравнение параболы, если расстояние от фокуса до директрисы равно 2.

Решение. Параметр p — это и есть данное расстояние от фокуса до директрисы. Подставляем и получаем:

Траектория камня, брошенного под углом к горизонту, летящего футбольного мяча или артиллерийского снаряда будет параболой (при отсутствии сопротивления воздуха). Зона достижимости для пущенных камней вновь будет параболой. В данном случае речь идёт об огибающей кривой траекторий камней, выпущенных из данной точки под разными углами, но с одной и той же начальной скоростью.

Парабола обладает следующим оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы, после отражения оказываются направленными параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, зеркала которых имеют вид параболоидов вращения (фигур, получающихся при вращении параболы вокруг оси). Пучок параллельных лучей, двигающийся вдоль оси параболы, отражаясь, собирается в её фокусе.