Уравнение падающего и отраженного лучей

Определение.

Закон отражения света имеет следующее определение: угол отражения равен углу падения. Падающий и отраженный лучи и перпендикуляр к поверхности зеркала в точке падения лежат в одной плоскости. Более подробно о физическом смысле закона и о том на базе чего он был сформулирован читайте далее в этой статье.

Небольшое вступление.

Если вы не знаете, что находится по ту сторону зеркала, спросите физика! Он скажет вам, что вы найдете там не перевернутую копию нашего мира, а другой, столь же загадочный мир физики. Он произнесет множество благозвучных физических названий, таких как видимый образ, закон отражения и луч света.

Хотя сегодня мы не можем представить себе жизнь без зеркал, или плоских стеклянных зеркал, их история не особенно длинна. Однако само явление отражения, благодаря которому зеркала могут существовать и работать, известно уже много веков и не менее увлекательно, чем они сами.

Видео:Законы преломления и отражения | Оптика | ЕГЭ по физике | Николай Ньютон. ТехноскулСкачать

Явление отражения света

Проведите наблюдение, которое позволит вам понять механизм формирования изображения при отражении световых лучей, как вы это наблюдаете на поверхности зеркала или поверхности воды.

Что вам понадобится?

• зеркало без рамы;
• фонарик с сильным светом (он может быть встроенным в телефон);
• расчёска;
• лист бумаги;
• линейка;
• карандаш;
• широкий пластырь или серебристая изоляционная лента.

Инструкция.

1. Нанесите ленту на зубья расчески так, чтобы в середине остались один или два зазора.
2. На листе бумаги проведите линию, перпендикулярную длинному краю бумаги.
3. На тот же край листа бумаги, лежащего на столе, вертикально положите отражающую сторону зеркала.
4. Положите расческу на стол вдоль длинного края бумаги напротив зеркала так, чтобы кончики зубцов были перпендикулярны столешнице.
5. Осветите расческу, чтобы один или два луча света прошли через незапечатанные щели.
6. Осветите зеркало так, чтобы свет фонарика падал на точку, где нарисованная линия пересекается с поверхностью зеркала.
7. Изменяйте угол освещения зеркала, располагая расческу под разными углами к листу бумаги — всегда держите фонарик так, чтобы свет падал на расческу перпендикулярно.
8. Что происходит с лучом света, отраженным от зеркала?

Подведём итог эксперимента.

Для того чтобы избежать двусмысленности в описании наблюдаемого нами явления, следует сначала выучить определения нескольких терминов.

В физике все гладкие поверхности, отражающие свет, называются зеркалами. Линия, перпендикулярная поверхности зеркала, называется нормалью. Свет фонаря падал в точку, где перпендикуляр (нормаль) пересекался с поверхностью зеркала. Угол между падающим лучом и перпендикуляром называется углом падения. Падающий луч отражается от поверхности зеркала, и получается отраженный луч. Угол между отраженным лучом и перпендикуляром называется углом отражения.

Наблюдения показали, что изменение угла, под которым свет фонаря падает на зеркало после прохождения через расчёску, влечет за собой изменение угла, под которым отражается падающий свет. Когда угол падения увеличивается, угол его отражения также увеличивается; когда он уменьшается, угол отражения также уменьшается.

Видео:Физика 9 класс (Урок№28 - Отражение света. Плоское зеркало.)Скачать

Закона отражения света

Изменяя угол падения, мы одновременно изменяем угол отражения. Угол падения и угол отражения вместе с перпендикуляром лежат в одной плоскости и равны друг другу.

Иллюстрация закона отражения света

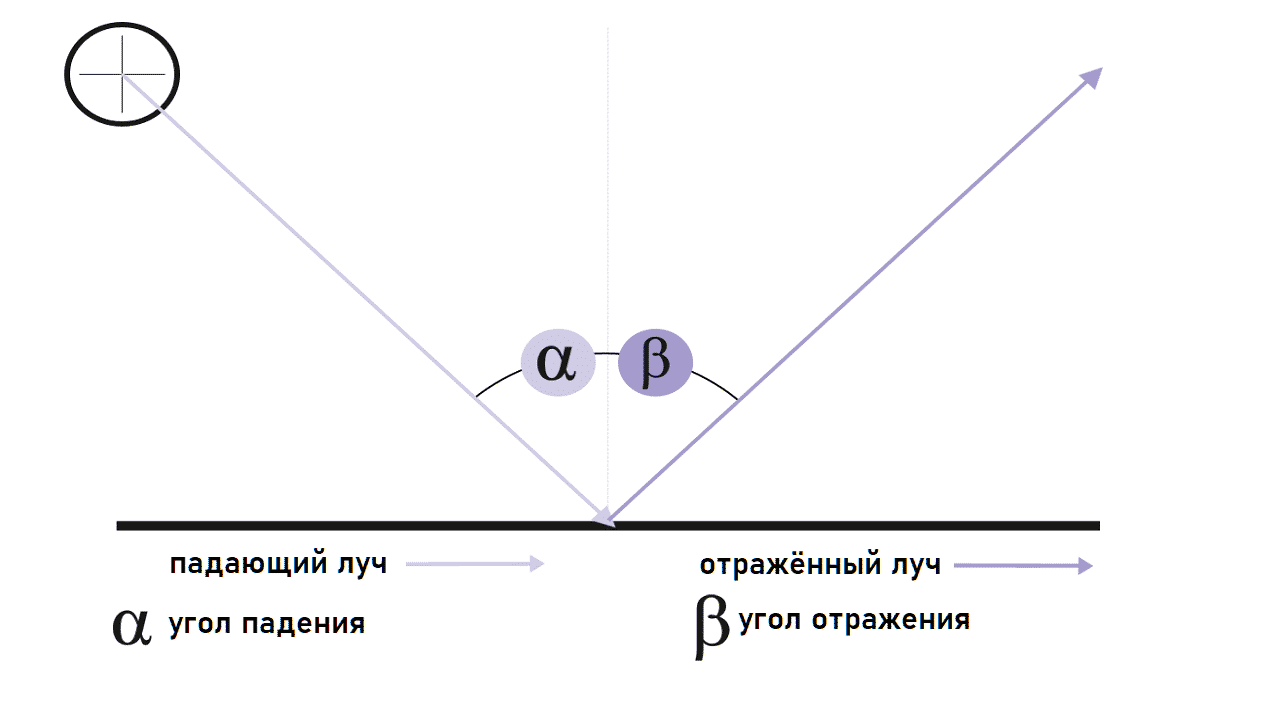
Формулировка закона и его формула.

Закон отражения света гласит так: угол отражения равен углу падения. Падающий и отраженный лучи и перпендикуляр к поверхности зеркала в точке падения лежат в одной плоскости.

В виде формулы закон отражения света записывается следующим образом: ∠ α = ∠ β.

Применение

Закон отражения используется во многих оптических системах. Повседневное значение имеют применения, описанные ниже.

Закон отражения используется для всех типов зеркал (плоские зеркала, вогнутые зеркала, выпуклые зеркала, параболические зеркала) и их применения (например, фары, фонари, косметические зеркала).

Он также используется для светоотражателей, которые должны быть установлены, например, на велосипедах. Они имеют гладкие стеклянные или пластиковые поверхности снаружи и множество маленьких призм внутри, на которых свет отражается таким образом, что выходит в том же направлении, откуда вошел. Поэтому велосипеды, находящиеся точно по направлению движения автомобиля, могут быть распознаны в темноте гораздо раньше, чем это было бы возможно без дополнительного оснащения светоотражателями.

Также закон отражения должен соблюдаться и в других местах. Гладкая поверхность воды отражает свет. И в тоже время, отражение тел видно на поверхности воды.

В помещениях, освещаемых сфокусированными прожекторами — например, на сцене театра — установка больших стеклопакетов может быть запрещена строительными нормами. Это связано с тем, что стекла воспринимаются только в том случае, если глаз смотрит на отраженный луч света. Для всех остальных людей существует опасность столкнуться со стеклом. В музеях, где много стеклянных витрин с точечным освещением, можно неоднократно наблюдать, как гости ударяются головой о стеклянную обшивку, потому что не заметили само стекло. Поэтому комнаты с большим количеством стеклянных витрин должны иметь рассеянное освещение.

Обратимость световых лучей

Световые пути обычно обратимы. Что это значит, показано на двух рисунках на рис. 2 на простом примере.

В левом изображении на рис. 2 свет исходит слева и отражается от зеркала. Читая угловую шкалу, можно увидеть, что закон отражения выполняется.

В правом изображении на рис. 2 луч света падает на зеркало точно с того направления, в котором луч света был отражен ранее. Вы видите, что теперь отраженный луч света проходит точно там же, где раньше проходил луч падающего света: поэтому путь света является обратимым.

Обратимость светового пути является важным основным принципом геометрической оптики, а также применима к гораздо более сложным явлениям, например, к преломлению света на воде.

Видео:Урок 198 (осн). Отражение света. Законы отраженияСкачать

Законы отражения света

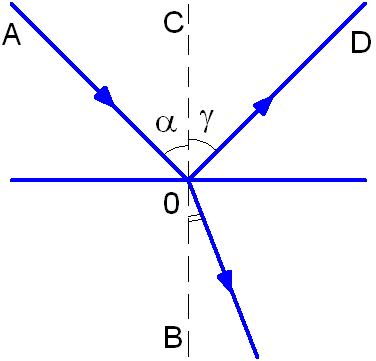
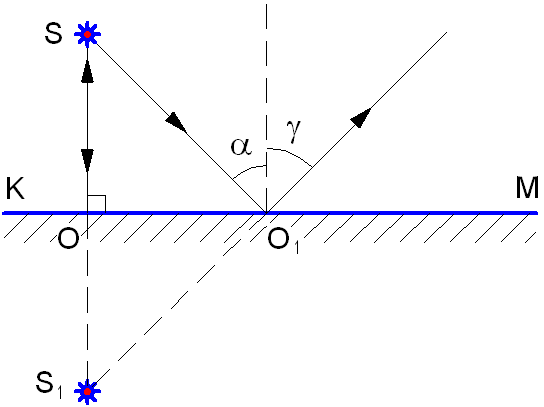
На границе раздела двух различных сред, если эта граница раздела значительно превышает длину волны, происходит изменение направления распространения света: часть световой энергии возвращается в первую среду, то есть отражается, а часть проникает во вторую среду и при этом преломляется. Луч АО носит название падающий луч, а луч OD – отраженный луч (см. рис. 1.3). Взаимное расположение этих лучей определяют законы отражения и преломления света.

Рис. 1.3. Отражение и преломление света.

Угол α между падающим лучом и перпендикуляром к границе раздела, восстановленным к поверхности в точке падения луча, носит название угол падения.

Угол γ между отражённым лучом и тем же перпендикуляром, носит название угол отражения.

Каждая среда в определённой степени (то есть по своему) отражает и поглощает световое излучение. Величина, которая характеризует отражательную способность поверхности вещества, называется коэффициент отражения. Коэффициент отражения показывает, какую часть принесённой излучением на поверхность тела энергии составляет энергия, унесённая от этой поверхности отражённым излучением. Этот коэффициент зависит от многих причин, например, от состава излучения и от угла падения. Свет полностью отражается от тонкой плёнки серебра или жидкой ртути, нанесённой на лист стекла.

Законы отражения света

Законы отражения света были найдены экспериментально ещё в 3 веке до нашей эры древнегреческим учёным Евклидом. Также эти законы могут быть получены как следствие принципа Гюйгенса, согласно которому каждая точка среды, до которой дошло возмущение, является источником вторичных волн. Волновая поверхность (фронт волны) в следующий момент представляет собой касательную поверхность ко всем вторичным волнам. Принцип Гюйгенса является чисто геометрическим.

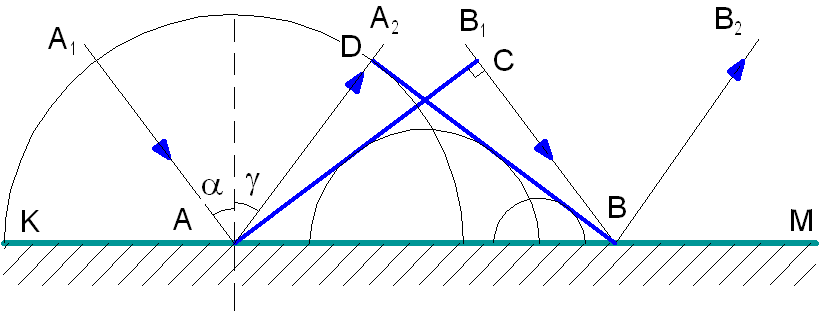
На гладкую отражательную поверхность КМ (рис. 1.4) падает плоская волна, то есть волна, волновые поверхности которой представляют собой полоски.

Рис. 1.4. Построение Гюйгенса.

А₁А и В₁В – лучи падающей волны, АС – волновая поверхность этой волны (или фронт волны).

Пока фронт волны из точки С переместится за время t в точку В, из точки А распространится вторичная волна по полусфере на расстояние AD = CB, так как AD = vt и CB = vt, где v – скорость распространения волны.

Волновая поверхность отражённой волны – это прямая BD, касательная к полусферам. Дальше волновая поверхность будет двигаться параллельно самой себе по направлению отражённых лучей АА₂ и ВВ₂.

Прямоугольные треугольники ΔАСВ и ΔADB имеют общую гипотенузу АВ и равные катеты AD = CB. Следовательно, они равны.

Углы САВ = = α и DBA = = γ равны, потому что это углы со взаимно перпендикулярными сторонами. А из равенства треугольников следует, что α = γ .

Из построения Гюйгенса также следует, что падающий и отражённый лучи лежат в одной плоскости с перпендикуляром к поверхности, восстановленным в точке падения луча.

Законы отражения справедливы при обратном направлении хода световых лучей. В следствие обратимости хода световых лучей имеем, что луч, распространяющийся по пути отражённого, отражается по пути падающего.

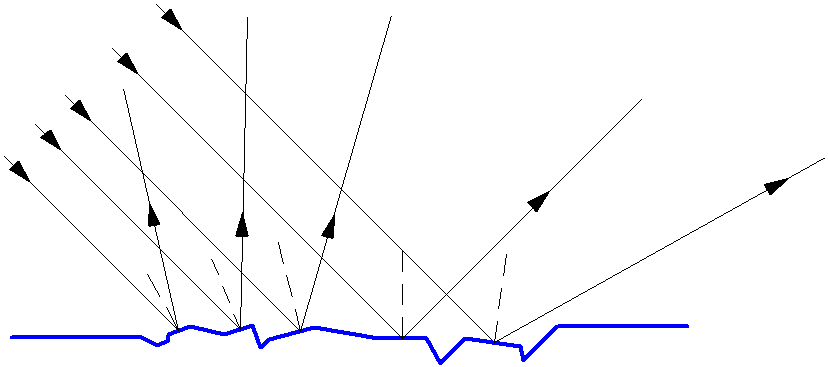
Большинство тел лишь отражают падающее на них излучение, не являясь при этом источником света. Освещённые предметы видны со всех сторон, так как от их поверхности свет отражается в разных направлениях, рассеиваясь. Это явление называется диффузное отражение или рассеянное отражение. Диффузное отражение света (рис. 1.5) происходит от всех шероховатых поверхностей. Для определения хода отражённого луча такой поверхности в точке падения луча проводится плоскость, касательная к поверхности, и по отношению к этой плоскости строятся углы падения и отражения.

Рис. 1.5. Диффузное отражение света.

Например, 85% белого света отражается от поверхности снега, 75% — от белой бумаги, 0,5% — от чёрного бархата. Диффузное отражение света не вызывает неприятных ощущений в глазу человека, в отличие от зеркального.

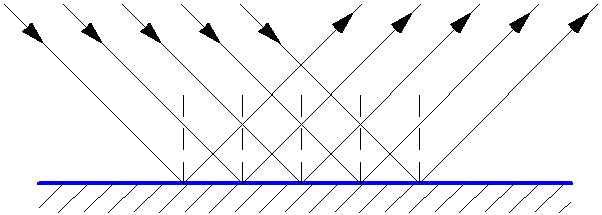
Зеркальное отражение света – это когда падающие на гладкую поверхность под определённым углом лучи света отражаются преимущественно в одном направлении (рис. 1.6). Отражающая поверхность в этом случае называется зеркало (или зеркальная поверхность). Зеркальные поверхности можно считать оптически гладкими, если размеры неровностей и неоднородностей на них не превышают длины световой волны (меньше 1 мкм). Для таких поверхностей выполняется закон отражения света.

Рис. 1.6. Зеркальное отражение света.

Плоское зеркало – это зеркало, отражающая поверхность которого представляет собой плоскость. Плоское зеркало даёт возможность видеть предметы, находящиеся перед ним, причём эти предметы кажутся расположенными за зеркальной плоскостью. В геометрической оптике каждая точка источника света S считается центром расходящегося пучка лучей (рис. 1.7). Такой пучок лучей называется гомоцентрическим. Изображением точки S в оптическом устройстве называется центр S’ гомоцентрического отражённого и преломлённого пучка лучей в различных средах. Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь от него, падает в глаз наблюдателя, то в зеркале видны изображения этих тел.

Рис. 1.7. Изображение, возникающее с помощью плоского зеркала.

Изображение S’ называется действительным, если в точке S’ пересекаются сами отражённые (преломлённые) лучи пучка. Изображение S’ называется мнимым, если в ней пересекаются не сами отражённые (преломлённые) лучи, а их продолжения. Световая энергия в эту точку не поступает. На рис. 1.7 представлено изображение светящейся точки S, возникающее с помощью плоского зеркала.

Луч SO падает на зеркало КМ под углом 0°, следовательно, угол отражения равен 0°, и данный луч после отражения идёт по пути OS. Из всего множества попадающих из точки S лучей на плоское зеркало выделим луч SO₁.

Луч SO₁ падает на зеркало под углом α и отражается под углом γ ( α = γ ). Если продолжить отражённые лучи за зеркало, то они сойдутся в точке S₁, которая является мнимым изображением точки S в плоском зеркале. Таким образом, человеку кажется, что лучи выходят из точки S₁, хотя на самом деле лучей, выходящих их этой точки и попадающих в глаз, не существует. Изображение точки S₁расположено симметрично самой светящейся точке S относительно зеркала КМ. Докажем это.

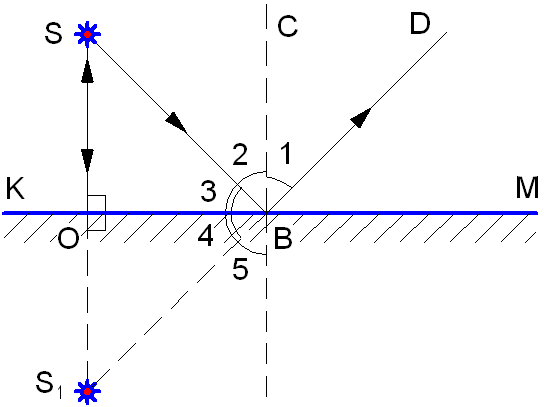
Луч SB, падающий на зеркало под углом 2 (рис. 1.8), согласно закону отражения света отражается под углом 1 = 2.

Рис. 1.8. Отражение от плоского зеркала.

Из рис. 1.8 видно, что углы 1 и 5 равны – как вертикальные. Суммы углов 2 + 3 = 5 + 4 = 90°. Следовательно, углы 3 = 4 и 2 = 5.

Прямоугольные треугольники ΔSOB и ΔS₁OB имеют общий катет ОВ и равные острые углы 3 и 4, следовательно, эти треугольники равны по стороне и двум прилежащим к катету углам. Это означает, что SO = OS₁, то есть точка S₁ расположена симметрично точке S относительно зеркала.

Для того чтобы найти изображение предмета АВ в плоском зеркале, достаточно опустить перпендикуляры из крайних точек предмета на зеркало и, продолжив их за пределы зеркала, отложить за ним расстояние, равное расстоянию от зеркала до крайней точки предмета (рис. 1.9). Это изображение будет мнимым и в натуральную величину. Размеры и взаимное расположение предметов сохраняются, но при этом в зеркале левая и правая стороны у изображения меняются местами по сравнению с самим предметом. Параллельность падающих на плоское зеркало световых лучей после отражения также не нарушается.

Рис. 1.9. Изображение предмета в плоском зеркале.

В технике часто применяют зеркала со сложной кривой отражающей поверхностью, например, сферические зеркала. Сферическое зеркало – это поверхность тела, имеющая форму сферического сегмента и зеркально отражающая свет. Параллельность лучей при отражении от таких поверхностей нарушается. Зеркало называют вогнутым, если лучи отражаются от внутренней поверхности сферического сегмента. Параллельные световые лучи после отражения от такой поверхности собираются в одну точку, поэтому вогнутое зеркало называют собирающим. Если лучи отражаются от наружной поверхности зеркала, то оно будет выпуклым. Параллельные световые лучи рассеиваются в разные стороны, поэтому выпуклое зеркало называют рассеивающим.

Видео:Отражение света, законы отражения, плоские зеркала. 8 класс.Скачать

Отражение и преломление света

Содержание:

Преломление света – явление изменения направления распространения света при прохождении через границу раздела сред с разными оптическими свойствами. Закон прямолинейного распространения света: в однородной оптической среде свет распространяется прямолинейно. Закон отражения света: луч падающий, луч отражённый и нормаль к отражающей поверхности в точке падения лежат в одной плоскости.

На странице -> решение задач по физике собраны решения задач и заданий с решёнными примерами по всем темам физики.

Видео:Закон преломления света. Полное отражение | Физика 11 класс #28 | ИнфоурокСкачать

Отражение и преломление света

Отражение света — это изменение направления световой волны при падении на границу раздела двух сред, в результате чего волна продолжает распространяться в первой среде.

Преломление света – это явление при котором лучи света меняют свое направление и расположение. Такое явление можно наблюдать поместив карандаш или любой продолговатый объект в стакан наполненный водой.

Световой луч и световой пучок

Световым лучом называется то направление, по которому распространяется свет. Так как светящаяся точка испускает свет по всем направлениям, то любая прямая, проведённая из этой точки, представляет световой луч.

Из нашего определения ясно, что световой луч есть понятие чисто геометрическое.

На практике свет всегда распространяется внутри прямолинейно ограниченного конуса, в виде светового пучка.

На рисунке 254 световой пучок изображён тремя лучами: осевым SO и лучами SА и SB, ограничивающими пучок.

Пучок света в чистом воздухе невидим; но если воздух содержит мелкие частички — пылинки, дым или мелкие капельки воды (туман), то благодаря освещённым частичкам пучок света становится видимым.

Во всяком действительном опыте, как уже указывалось, мы имеем дело не со световым лучом, а со световым пучком. Смотря по тому, как он ограничен, мы различаем параллельный, расходящийся и сходящийся пучки (рис. 255).

При помощи диафрагм ширина пучка может быть сделана малой, но не произвольно малой. При уменьшении размеров отверстия диафрагмы, через которое проходит пучок лучей, прямолинейность лучей постепенно нарушается—свет начинает заходить в область тени (на это же указывалось в § 127).

Наш глаз обычно воспринимает расходящиеся пучки лучей, и в месте пересечения этих лучей мы видим светящуюся точку. При этом возможны два случая: 1) точка пересечения лучей действительно существует; тогда видимую светящуюся точку называют действительной; 2) расходящийся пучок лучей не имеет действительной точки пересечения, но глазу она представляется существующей в месте пересечения воображаемых продолжений расходящихся лучей; такая точка называется мнимой. Однако ничего мнимого здесь нет. Где-то существует реальная светящаяся точка, из которой вышли лучи, попавшие в наш глаз. Но не всегда мы видим её там, где на самом деле она находится, и в этом смысле употребляется термин «мнимая точка».

Отдел учения о свете, в котором явления распространения света рассматриваются на основе представлений о световом луче, называется геометрической или лучевой оптикой.

Явления, происходящие при падении света на тела

Когда свет падает на какое-нибудь тело, то, во-первых, часть падающего света отражается от поверхности тела. Такое явление называется отражением света.

Во-вторых, часть света проникает внутрь тела и может распространяться в нём дальше. При этом на поверхности тела эта часть света может изменить первоначальное направление и дальше в теле распространяться по другому направлению. Это явление называется преломлением света.

Если сложить отражённый и преломлённый световые потоки, то их сумма будет равна величине полного светового потока, падающего на тело. Но в процессе распространения света внутри тела интенсивность света постепенно уменьшается вследствие поглощения его средой. При этом световая энергия превращается в другие виды энергии, в частности, она может перейти во внутреннюю энергию тела. Хорошо известно, например, что под действием света тела нагреваются.

Относительная величина отражённого и преломлённого света определяется рядом факторов: веществом тела, состоянием его поверхности, составом самого света, углом падения и др.

Поглощение также зависит от вещества тела и от состава светового потока.

Итак, при падении света на поверхность тела можно наблюдать явления отражения и преломления, а при прохождении его в теле — явление поглощения света.

Законы отражения света

Познакомимся с законами отражения света на опыте.

Установим плоское зеркальце РР в центре кругового диска, разделённого на градусы, так, чтобы лучи падали к основанию перпендикуляра CN, восставленного к плоскости зеркальца (рис. 256). Пусть SC — падающий луч, a — отражённый луч. Точка С — точка падения луча. Угол SCN между падающим лучом SC и перпендикуляром CN называется углом падения. Угол между отражённым лучом и тем же перпендикуляром CN называется углом отражения.

Из опыта видно, что луч падающий и луч отражённый лежат в одной плоскости с перпендикуляром к зеркалу, проведённым из точки падения луча.

Вращая диск, будем менять угол, под которым падает луч на зеркальце, мы заметим, что при этом меняется и угол отражения.

Измеряя каждый раз угол падения и соответствующий ему угол отражения, можно установить, что они равны друг другу.

Таким образом, отражение света происходит по следующим законам:

1. Отражённый луч лежит в той же плоскости, в которой лежат падающий луч и перпендикуляр к отражающей поверхности, восставленный в точке падения луча.
2. Угол отражения равен углу падения.

Если падающий луч идёт по направлению , то, строя ход отражённого луча согласно сформулированным выше законам отражения, найдём, что отражённый луч пойдёт по Следовательно, падающий и отражённый лучи света взаимообратимы.

Диффузное и зеркальное отражения

Громадное большинство видимых нами тел не являются источниками света и видимы только в том случае, если на них попадает свет от какого-либо источника. Но видеть предметы мы можем только тогда, когда к нам в глаз попадают лучи света. Таким образом, мы приходим к тому выводу, что освещённые тела отражают свет. При этом следует различать рассеянное (диффузное) отражение от зеркального отражения.

При рассеянном отражении отражённые от предмета лучи распространяются во все стороны, вследствие чего предмет мы видим со всех сторон. Диффузно отражает свет, например, обычный лист бумаги (рис. 257).

Диффузно отражающую поверхность можно представить в виде элементарных плоскостей, различно расположенных и пересекающихся под различными углами. Но если падающий на тело параллельный пучок лучей света отражается в одном определённом направлении, то в этом случае мы говорим о зеркальном отражении (рис. 258). Зеркально отражают свет, например, тщательно отполированные металлы.

Плоское зеркало

Плоским зеркалом называют плоскую поверхность, зеркально отражающую свет.

Пусть MN (рис. 259) — плоское зеркало, S — светящаяся точка, находящаяся перед зеркалом. Из этой точки лучи выходят по разным направлениям: и т. д. От поверхности зеркала эти лучи отражаются и идут по направлениям AD, BE, CF и т. д.

расходящимся пучком. Если такой расходящийся пучок лучей попадёт в глаз, то нам будет казаться, что эти лучи выходят из точки , находящейся на пересечении продолжения этих лучей за зеркалом. Нетрудно доказать из равенства прямоугольных треугольников , что точка находится за зеркалом на таком же расстоянии от него, на каком точка S находится перед зеркалом.

Две точки называются симметричными по отношению к плоскости зеркала, причём точка называется мнимым изображением светящейся точки S.

Зная, как строится изображение светящейся точки, легко построить изображение предмета. Пусть АВ — лицо (рис. 260), находящееся перед зеркалом MN. Все точки этого лица дадут симметричные мнимые изображения за зеркалом. Так, например, изображением точки А будет точка точки В — точка и т.д. Изображение всего лица АВ в зеркале будет иметь ту же величину, что и само лицо, и будет расположено симметрично ему.

Изображение предмета в плоском зеркале, так же как и изображение точки, будет мнимым.

Вогнутое сферическое зеркало

Сферическое зеркало представляет собой тщательно отполированную поверхность шарового сегмента. Сферические зеркала бывают вогнутыми и выпуклыми. Центр шаровой поверхности С называется оптическим центром зеркала (рис. 261); вершима шарового сегмента О — полюсом зеркала.

Всякая прямая, проходящая через оптический центр зеркала С, называется оптической осью зеркала. Оптическая ось СО, проходящая через центр сферы С и полюс зеркала О, называется главной оптической осью.

Угол , образуемый двумя лежащими в одной плоскости с осью радиусами, проведёнными к краям зеркала, называется угловым отверстием зеркала или апертурой.

Лучи, идущие вблизи главной оптической оси, называются осевыми или центральными лучами. Все наши дальнейшие выводы будут относиться именно к таким лучам.

Если на вогнутое зеркало пустить пучок лучей, параллельных главной оптической оси, то лучи эти, отразившись от зеркала, сойдутся в небольшой области пространства, лежащей на оси приблизительно на середине радиуса.

Если такой опыт произвести с солнечными лучами и поместить в то место, в котором сходятся отражённые от зеркала лучи, какое-нибудь тело, то оно будет сильно освещено и даже нагреется, а легко воспламеняющееся вещество может даже загореться.

По этой причине вогнутые зеркала называются собирающими.

Фокус вогнутого сферического зеркала

Пусть на вогнутое зеркало падает осевой луч SA параллельно главной оптической оси зеркала ОС (рис 262). Проведём из центра С сферической поверхности зеркала перпендикуляр СА и построим отражённый луч АВ. Этот луч пересечёт оптическую ось в точке F. Легко показать, что эта точка расположена на половине расстояния ОС, т. е.

— радиус сферической поверхности зеркала.

В самом деле, как внутренние накрест лежащие углы. Но есть угол падения луча, следовательно, и угол отражения луча В треугольнике CFA CF=AF, но так как луч SA— центральный луч, то точки A и О близки друг другу, а это значит, что OF=AF; отсюда что и требовалось доказать.

Точка F, в которой центральный луч. параллельный главной оптической оси зеркала, после отражения пересекает эту ось зеркала, называется фокусом зеркала.

Расстояние OF от вершины зеркала до фокуса называется фокусным расстоянием. Для краткости оно обозначается одной буквой F.

В фокусе собирается после отражения от зеркала весь центральный пучок лучей, падающий на зеркало параллельно главной оптической оси зеркала (рис. 263).

Плоскость, проходящая через фокус перпендикулярно глазной оптической оси, называется фокальной плоскостью.

На рисунке 264 светящаяся точка S расположена перед вогнутым зеркалом. Проведём от неё к зеркалу три центральных луча

и, согласно законам отражения, построим отражённые лучи. Все три отражённых луча пересеклись в одной точке . Так как мы взяли три произвольных центральных луча, то и все прочие центральные лучи, исходящие из точки S, тоже пересекутся в точке . В таком случае будет изображением точки S. Если расположить глаз так, как показано на рисунке 264, то мы увидим в точке светящуюся точку. Следовательно, после отражения от зеркала центральные лучи, исходящие из различных точек предмета, должны пересечься в соответствующих точках и совокупность их — образовать изображение предмета. Проверим это на опыте.

Установив зажжённую свечу перед зеркалом примерно так, как показано на рисунке 265, и расположив соответствующим образом глаз, мы действительно увидим перед зеркалом (при данном расположении свечи относительно зеркала) уменьшенное и обратное изображение свечи. Если там, где мы увидели изображение, поместить лист белой бумаги, то на нём получится изображение пламени свечи, видное со всех сторон, так как белый лист бумаги отражает свет диффузно.

Таким образом, опыт подтверждает наше предположение, что все центральные лучи, исходящие из одной точки, после отражения от вогнутого зеркала пересекаются тоже в одной точке.

Построение изображений в вогнутом зеркале

Мы видели, что все центральные лучи, исходящие из светящейся точки после отражения от сферического зеркала, пересекаются в одной точке, т. е. после отражения от зеркала «точечный» источник света даёт точечное изображение.

Поэтому для изображения точки достаточно знать направление распространения только двух лучей, выходящих из этой точки: их точка пересечения будет точкой пересечения и других лучей, исходящих из данной точки. Лучи эти могут быть выбраны совершенно произвольно, но удобнее всего пользоваться определёнными лучами, направление распространения которых после отражения заранее известно. Изображение предмета складывается из совокупности изображений отдельных точек этого предмета.

Допустим, что нам нужно построить изображение предмета AВ в вогнутом зеркале (рис. 266а).

Проводим из точки А два луча: один — параллельно главной оптической оси, второй — через оптический центр С, после отражения от зеркала первый пройдёт через фокус F, второй — обратно по тому же направлению. Через точку пересечения этих лучей пройдут и все остальные лучи, выходящие из точки А и отразившиеся от зеркала: точка будет изображением точки А. Таким же образом построим и изображение точки В, это будет точка . Изображения остальных точек предмета АВ расположатся между точками и и, следовательно, будет изображением предмета АВ.

На рисунке 266 б предмет АВ находится между фокусом и зеркалом. Изображение предмета — увеличенное и мнимое.

В зависимости от положения предмета по отношению к зеркалу его изображения могут быть действительные и мнимые, прямые и обратные, увеличенные и уменьшённые. На рисунке 267 показана установка для получения изображений лампочки в вогнутом зеркале.

Применение вогнутых зеркал

Вогнутые зеркала находят весьма широкое применение в науке и технике. Например, вогнутыми зеркалами пользуются в тех случаях, когда нужно направить в какое-либо место концентрированный пучок света. Так устраиваются осветители в автомобильных, проекционных и карманных фонарях. В каждом из них за источником света помещается вогнутое зеркало. Примером может служить автомобильная фара, изображённая на рисунке 268.

Вогнутые зеркала (параболические) находят чрезвычайно важное применение при устройстве прожекторов. Прожектор состоит из двух главных частей: мощного источника света (электрической дуги) и большого вогнутого зеркала, помещаемого сзади источника света так, чтобы источник света оказался в фокусе зеркала.

Прожектор как осветитель применяется при киносъёмках, при освещении строительных площадок, стадионов, площадей.

В военном деле прожекторы употребляются для освещения и сигнализации.
Вогнутые зеркала находят весьма важное применение при устройстве телескопов-рефлекторов.

Выпуклое зеркало

Пусть MN — выпуклое зеркало (рис. 269). Поместим перед ним светящуюся точку S и построим её изображение.

Лучи от этой точки после отражения идут расходящимся пучком. Вершина этого пучка лежит за зеркалом в точке пересечения продолжения расходящихся лучей . В этой точке, как было уже указано в § 135, мы и увидим мнимое изображение светящейся точки S. Где бы предмет ни находился относительно выпуклого зеркала, его изображение в зеркале всегда мнимое и уменьшенное. Построение изображения предмета в выпуклом зеркале показано на рисунке 270; здесь АВ —предмет, а — его изображение.

Законы преломления света

Когда луч света падает на гладкую поверхность прозрачной среды, то образуется не один только отражённый луч. Из точки падения луча выходит ещё второй луч, распространяющийся во второй прозрачной среде, его называют преломлённым лучом. Направление преломлённого луча не совпадает с направлением падающего луча, однако между ними существует определённая г связь, которую можно установить на опыте.

На рисунке 271а пучок света падает на полированную поверхность стеклянной пластинки. На границе, разделяющей стекло и воздух, этот пучок раздваивается на два пучка; один из них отражается от поверхности стекла, другой же переходит в стекло, резко изменив своё направление. SO — осевой луч падающего пучка света; — отражённого и — преломлённого пучка.

Сравнив направление преломлённого луча с направлением перпендикуляра On, проведённого к границе в точке падения, мы увидим, что преломлённый луч лежит по ту же сторону перпендикуляра, где находится и луч отражённый . Угол — угол падения луча; обозначим его буквой ; угол между преломлённым лучом и перпендикуляром On называется углом преломления; обозначим его буквой . При изменении угла падения меняется и угол преломления. Угол преломления равен нулю, когда угол падения равен нулю; с увеличением же угла падения увеличивается и угол преломления; однако всё время угол преломления остаётся меньше угла падения.

На рисунке 271 б изображена установка для наблюдения явления преломления света при переходе из воздуха в воду и из воды в воздух.

Возьмём стеклянную пластинку, нижняя грань которой параллельна верхней и покрыта тонким слоем серебра (рис. 272). Пустим на пластинку луч света под углом и проследим ход его из стекла в воздух. Мы заметим, что в этом случае угол преломления всегда больше угла падения. Упав на нижнюю грань под углом , луч отразится от неё и, встретив под этим углом верхнюю грань, выйдет в воздух под некоторым углом . Измерив углы можно убедиться, что они равны: Если падающий луч будет пущен по направлению преломлённого луча, то луч преломлённый пойдёт по линии луча падающего, т. е. луч падающий и луч преломлённый взаимообратимы.

На основании опытов были установлены следующие законы преломления света:

• 1. Преломлённый луч лежит в той же плоскости, в которой лежат падающий луч и перпендикуляр, восставленный в точке падения луча к границе раздела двух сред.
• 2. При всех изменениях углов падения и преломления отношение синуса угла падения ксинусу угла преломления для данных двух сред есть величина постоянная, называемая показателем преломления второй среды относительно первой.

Математически этот закон можно написать в виде следующей формулы:

где — угол падения, — угол преломления и п — показатель преломления.

Показатель преломления данного вещества по отношению к вакууму называется абсолютным показателем преломления этого вещества.

Практически показатель преломления определяется обычно относительно воздуха, а не относительно вакуума. Чтобы получить показатель преломления данного вещества относительно вакуума, надо значение показателя преломления этого вещества относительно воздуха умножить на абсолютный показатель преломления воздуха, равный 1,0003.

Величина показателя преломления для данного вещества зависит от цветности лучей света.

Несколько значений показателей преломления для красного света даны в нижеследующей таблице.

При сравнении двух веществ то из них, которое имеет больший показатель преломления, называется оптически более плотным.

Понятие показателя преломления имеет глубокое физическое содержание. Абсолютный показатель преломления (п) указывает, во сколько раз скорость света в вакууме (с) больше скорости света () в данном веществе, т. е.

Этот важный вывод вытекает из волновой теории распространения света, основы которой будут изложены в главе IX.

Полное отражение света

Рассмотрим подробнее случай перехода света из оптически более плотной среды в менее плотную.

Пусть на границу MN стекло — воздух из стекла падает расходящийся пучок света. Определим его тремя лучами — двумя крайними I и III и осевым II (рис. 273,а). У границы часть пучка отразится в стекло, часть перейдёт в воздух. Будем постепенно увеличивать угол падения. Мы заметим, что по мере возрастания угла падения яркость отражённого пучка будет возрастать, а преломлённого уменьшаться. При некотором угле падения луч I будет скользить по поверхности раздела (рис. 273,6). При увеличении угла падения то же произойдёт и с осевым лучом // и, наконец, с лучом ///. При дальнейшем увеличении угла падения луча /// преломлённого пучка уже не будет, весь падающий пучок отразится в стекло (рис. 273, е). Такое явление называется полным отражением.

Наименьший угол падения, при котором наступает полное отражение, называется предельным углом полного отражения.

Таким образом, полное отражение наблюдается при переходе света из оптически более плотной среды в менее плотную в том случае, если все лучи заданного пучка падают под углом, большим предельного.

Предельному углу падения соответствует угол преломления, равный 90°. Пусть показатель преломления стекла относительно воздуха — п; тогда на основании закона преломления света и свойства обратимости луча можно написать:

отсюда

Из полученного соотношения вычисляется предельный угол полного отражения. Для воды (n=1,33) этот угол равен 48°,5, для стекла (n=1,51) 42°, а для алмаза (п = 2,4) предельный угол равен 24°,5.

Полное отражение широко используется в различных оптических приборах, например в полевых биноклях, перископах и т. д.

Полным отражением объясняется целый ряд явлений, например блеск капель росы при солнечном свете, светящиеся фонтаны, блеск («игра») бриллиантов, образование миражей и т. д.

Изменение светового потока при отражении и преломлении

Допустим, что свет, падающий на границу раздела двух сред, не поглощается второй средой. Часть светового потока отражается от поверхности раздела сред, другая же часть проникает во вторую среду и распространяется в ней. При таких условиях

Из этого равенства следует, что как отражённая, так и преломлённая части потока света в отдельности не равны падающему потоку света; это легко можно заметить и в наших опытах (рис. 273). Кроме того, опыт показывает, что при малых углах падения преломлённый поток света значительно больше отражённого. По мере же увеличения угла падения увеличивается и отражённый поток, между тем как преломлённый поток уменьшается.

Кроме того, отражённый поток света зависит от оптических свойств тех двух сред, граница между которыми отражает свет. Оказывается, чем больше разница между показателями преломления обеих сред, тем больший поток отражается. Если показатели преломления обеих сред одинаковы, то свет вообще не отражается.

Так, например, показатель преломления кедрового масла весьма близок к показателю преломления стекла; поэтому стеклянная палочка, погружённая в кедровое масло, невидима (несветящиеся тела мы видим благодаря отражённому свету). Этим свойством веществ пользуются для склеивания стёкол в оптических приборах, подбирая такие склеивающие вещества, показатель преломления которых близок к показателю преломления стекла.

Прохождение света через прозрачную пластинку с параллельными гранями

Практически большое значение имеет случай, когда свет переходит из одной среды в другую и затем снова выходит в первую, т. е. свет проходит через какое-либо оптически прозрачное тело. Поверхности раздела могут быть при этом самыми разнообразными. Мы прежде всего разберём случай, когда свет проходит через пластинку, ограниченную параллельными плоскостями.

Пусть — плоско-параллельная пластинка (рис. 274). Легко показать, что луч SO пучка света, падающего на пластинку, после двух преломлений выйдет наружу по направлению , параллельному SO.

Обозначим угол падения луча SO через , а угол преломления через . Вследствие параллельности плоскостей луч, пройдя стекло, встретит плоскость пластинки под углом и, следовательно, выйдет из неё под углом Таким образом, при прохождении через плоско-параллельную пластинку луч света не изменяет своего направления, он только смещается. Чем толще пластинка, тем значительнее будет это смещение. Если рассматривать предмет через плоско-параллельное стекло, то он будет казаться нам сдвинутым относительно своего истинного положения.

Прохождение света через прозрачную треугольную призму

На рисунке 275а АВ и АС — плоские поверхности призмы, ограничивающие её преломляющий угол . Плоскость чертежа

перпендикулярна к обеим преломляющим поверхностям призмы и представляет собой сечение призмы. Пусть на грань АВ этой призмы падает какой-нибудь одноцветный, например красный, пучок лучей света (на рис. 275а показан только осевой луч DE этого пучка). В точке Е луч DE преломится и пойдёт внутри призмы по направлению EF. У грани АС этот луч ещё раз преломится, отклоняясь к грани ВС. Вышедший из призмы луч света после двукратного преломления отклонится на угол . Величина угла отклонения зависит от преломляющего угла призмы и показателя преломления вещества призмы п. Если рассматривать какой-либо предмет через треугольную призму, то предмет покажется смещённым к вершине угла, образованного плоскостями, через которые проходят лучи от источника (рис. 275 б).

Если пропускать пучок лучей на одну из граней стеклянной равнобедренной прямоугольной призмы ABC (рис. 276), то внутри призмы лучи отразятся от грани призмы АС, испытав полное отражение, так как в этом случае угол падения лучей на грань АС больше 42°, т. е. больше предельного угла для стекла. Прямоугольная призма ABC в положениях, показанных на рисунке, может быть использована для поворота светового пучка на 90° и для обращения какого-либо изображения, получающегося в оптическом приборе. В последнем случае нижние лучи, отразившись внутри призмы от грани АС, по выходе из призмы становятся верхними, а верхние — нижними. Такая призма называется оборотной и применяется во многих оптических приборах, в частности в призматическом бинокле.

Линзы

Прозрачные для света тела, ограниченные с двух сторон сферическими или иными кривыми поверхностями (одна из двух поверхностей может быть плоской), называются оптическими стёклами или линзами.

По форме ограничивающих поверхностей линзы могут быть сферическими, цилиндрическими и другими (в дальнейшем будут рассматриваться только сферические линзы).

Линзы, у которых середина толще, чем края, называются выпуклыми; те же линзы, у которых края толще середины, называются вогнутыми.

На рисунке 277 изображены в поперечном разрезе различные виды сферических линз: 1, 2, 3 — выпуклые линзы; 4, 5, 6—вогнутые линзы.

Пустим параллельный пучок лучей света на выпуклую линзу, а за линзой поместим экран. Перемещая экран относительно линзы, мы получим на нём небольшое светлое пятно. Выпуклая линза, преломляя падающие на неё лучи, собирает их. Поэтому такая линза называется собирающей. Вогнутая же линза, преломляя свет, рассеивает его в стороны. Такая линза называется рассеивающей.

Рисунок 278 поясняет действие собирающих и рассеивающих линз. Собирающую линзу можно представить в виде совокупности большого числа призм, расширяющихся к середине линзы, а рассеивающую — как совокупность большого числа призм, расширяющихся к краям.

Известно, что каждая призма отклоняет лучи света к грани, лежащей против преломляющего угла; величина отклонения зависит от величины отклоняющего угла. Понятно, что линзы с утолщением на середине отклоняют лучи к середине, собирая их, линзы же с утолщением по краям отклоняют лучи к краям, т. е.

рассеивают их. Середина линзы действует как плоско-параллельная пластинка.

Мы будем рассматривать только очень тонкие линзы, в которых расстояние между краями очень мало по сравнению с расстояниями (рис. 279). В таких линзах практически точки можно считать сливающимися в одной точке О. Эту точку О называют оптическим центром линзы.

Всякая прямая, проходящая через оптический центр, называется оптической осью линзы. Оптическая ось, проходящая через центры сферических преломляющих поверхностей , образующих линзу, называется главной оптической осью линзы (рис. 279), другие — побочными осями.

Луч света, идущий по какой-либо из оптических осей, проходит тонкую линзу, не меняя своего направления.

Фокус линзы

Если направить на собирающую линзу осевой луч SE, параллельный её оси (рис. 280), то, пройдя линзу, этот луч пересечёт ось на определённом расстоянии от линзы —

в точке F. Расстояние OF называется фокусным расстоянием линзы, а самая точка F называется фокусом линзы. У всякой линзы два фокуса, по обе стороны её.

Основываясь на законах преломления света, можно теоретически доказать, что все осевые лучи, т. е. лучи, идущие вблизи главной оптической оси, падающие на тонкую собирающую линзу параллельно её оси, сходятся в фокусе. Опыт подтверждает это теоретическое доказательство (рис. 281).

Пустив пучок осевых лучей параллельно главной оптической оси на тонкую двояковогнутую линзу (рис. 282), мы заметим, что из линзы лучи выйдут расходящимся пучком. Если такой расходящийся пучок попадёт в наш глаз, то нам будет казаться, что лучи выходят из одной точки F. Эта точка называется мнимым фокусом двояковогнутой линзы.

Плоскость MN, проведённая через фокус линзы перпендикулярно к главной оптической оси, называется фокальной плоскостью линзы (рис. 283). Фокальных плоскостей у линзы две, и расположены они по обе стороны линзы.

Когда на линзу падает пучок лучей, параллельных какой-либо побочной оптической оси, то после преломления в линзе он сходится на соответствующей побочной оптической оси в месте её пересечения с фокальной плоскостью (рис. 283).

Оптическая сила линзы

Величина, обратная фокусному расстоянию линзы F, называется оптической силой D линзы:

За единицу оптической силы линзы принимается оптическая сила такой линзы, фокусное расстояние которой равно 1 м; такая единица называется диоптрией.

У выпуклых линз оптическая сила положительна, у вогнутых — отрицательна.
Пример. Чему равна оптическая сила очковой выпуклой линзы, фокусное расстояние которой F=50 см?

Величина фокусного расстояния линзы, а следовательно, и её оптическая сила определяются показателем преломления вещества линзы и радиусами сферических поверхностей, её ограничивающих.

Теория даёт формулу, по которой можно рассчитать оптическую силу линзы:

В этой формуле п — показатель преломления вещества линзы, — радиусы кривизны поверхностей линзы. Радиусы выпуклых поверхностей считаются положительными, вогнутых — отрицательными.

Изображение точки в собирающей линзе

Теория показывает и опыт подтверждает, что осевые лучи, вышедшие из одной светящейся точки, после прохождения через линзу сходятся также в одной точке, которая называется изображением первой точки.

Этим важным положением можно воспользоваться для нахождения изображения светящейся точки в собирающей линзе путём геометрического построения хода центральных (осевых) лучей.

Так как все центральные лучи, выходящие из одной точки, пройдя через собирающую линзу, сходятся в одной точке, то для построения изображения её достаточно найти точку пересечения каких-либо двух лучей.

Построим, например, изображение светящейся точки (рис. 284а). Проще всего это можно выполнить при помощи лучей, указанных на этом рисунке. Один из них — луч SC, параллельный главной оптической оси, преломившись в линзе, пройдёт через фокус линзы F; другой луч SD, идущий из точки S через фокус F, за линзой пойдёт параллельно оси линзы. Третий луч SO пройдёт через оптический центр линзы, не преломляясь. Ход всякого иного луча, выходящего из точки S, нужно было бы строить, применяя законы преломления света, что значительно сложнее. Но в этом нет никакой необходимости, так как все центральные (осевые) лучи, выходящие из точки S, преломившись в линзе, обязательно пройдут через точку .

Построим изображение точки S, лежащей на оптической оси линзы (рис. 2846). Для этого проведём из точки S на линзу какой-нибудь луч. Параллельно этому лучу проведём побочную оптическую ось ВС, которая пересечёт фокальную плоскость MN в точке С. После преломления в линзе через точку С пройдёт весь

пучок света, параллельный побочной оптической оси ВС; следовательно, через эту точку пройдёт и луч SA. Главную оптическую ось этот луч пересечёт в точке , которая и является изображением точки S. Второй луч из S направлен вдоль главной оптической оси.

Выбранные нами лучи для построения изображения точки не обязательно должны пройти через линзу.

Так, например, на рисунке 285 лучи SA и SB не проходят через линзу, но могут быть использованы для построения изображения точки, которое, очевидно, определится пучком реальных лучей, вышедших из точки S и ограниченных размерами линзы. Этот реальный пучок, преломившись в линзе, пройдёт через точку .

Изображение предметов в собирающей линзе

Рассматривая предмет как совокупность точек и пользуясь свойством центральных лучей, выходящих из точки после преломления в линзе, собираться также в точке, можно геометрически построить изображение предмета в линзе.

Построим, например, изображение предмета АВ в собирающей линзе (рис. 286). Для этого достаточно построить изображение двух его крайних точек А и В. При построении же изображения, например точки A, проще всего провести из этой точки два луча: один параллельно главной оптической оси линзы, другой через оптический центр линзы, т. е. по побочной оптической оси .

После прохождения линзы оба луча пересекутся в точке . Таким же способом строим изображение точки В. Изображения остальных точек предмета расположатся между точками . Таким образом, является изображением предмета АВ. Изображение — действительное, обратное и уменьшённое.

На рисунке 287 показано построение изображения предмета, расположенного относительно линзы на расстоянии, меньшем фокусного расстояния. В этом случае изображение получается мнимое.

Характер получаемого от линзы изображения предмета, т. е. его величина и положение, зависит от положения предмета относительно линзы. Местонахождение изображения предмета и его величина могут быть найдены с помощью формулы линзы.
На рисунке 288 показана установка для получения изображения с помощью линзы.

Формула линзы

Для вывода формулы линзы воспользуемся рисунком 289. Здесь АВ — предмет, — его изображение. Исходя из подобия прямоугольных треугольников FOC и , можно написать:

Из подобия треугольников имеем:

Так как АВ=ОС, то левые части равенств (1) и (2) равны между собой. Приравнивая правые части этих равенств, мы получим:

или, заменяя — расстояние изображения от линзы, ВО=d— расстояние предмета от линзы, получим:

откуда

или

Разделив обе части последнего равенства на получим формулы линзы:

Отсчёт расстояний d, f и F производится от оптического центра линзы. Величины d и F, входящие в формулу выпуклой линзы, всегда положительные, величина же f в случае мнимых изображений отрицательна; она откладывается по ту же сторону от центра линзы, что и величина d.

Отношение линейного размера изображения к размеру предмета АВ называется линейным увеличением линзы.

Обозначая линейное увеличение буквой k, получаем:

Так как то из этого следует, что линейное увеличение линзы

Двояковогнутая линза

Построим изображение точки, даваемое двояковогнутой линзой. Лучи от светящейся точки S после прохождения линзы идут расходящимся пучком (рис.290), но нам будет казаться, что эти лучи выходят из одной точки, находящейся перед линзой, из точки , которая и является мнимым изображением точки S.

Проделав опыт с двояковогнутой линзой, легко убедиться, что изображения предметов в ней всегда мнимые, уменьшённые и прямые, независимо от того, на каком расстоянии от линзы находится предмет.

Видео:Поляризация света и угол БрюстераСкачать

Отражение и преломление света и его определение

Свет — это электромагнитные колебания определенного диапазона длин волн — видимое оптическое излучение (от фиолетового до красного), которые воспринимает человеческий глаз.

Отражение света — это изменение направления световой волны при падении на границу раздела двух сред, в результате чего волна продолжает распространяться в первой среде.

Преломление света – явление изменения направления распространения света при прохождении через границу раздела сред с разными оптическими свойствами. Закон прямолинейного распространения света: в однородной оптической среде свет распространяется прямолинейно. Закон отражения света: луч падающий, луч отражённый и нормаль к отражающей поверхности в точке падения лежат в одной плоскости, причём угол падения равен углу отражения.

Оптические явления на границе раздела двух прозрачных сред

Вспомним, что в однородной среде свет распространяется прямолинейно. Это дает возможность при описании распространения света в такой среде пользоваться световыми лучами.

Изменение направления распространения света происходит на границе раздела двух различных сред. Поэтому, если установить из опытов законы, позволяющие точно определять такие изменения, то с помощью световых лучей можно описывать ход многих оптических явлений, не учитывая физической природы светового излучения. Часть оптики, в которой используется такой метод описания явлений, называют геометрической оптикой. В этой главе рассматриваются законы, которым подчиняются оптические явления, происходящие на границе раздела двух прозрачных сред.

Когда на поверхность воды из воздуха падает тонкий пучок света (рис. 29.1), то можно заметить, что в точке падения О часть света отражается, а часть проникает в воду и при этом преломляется. Вспомним, что углы и соответственно называют углом падения и углом отражения (§ 24.19). Угол составленный преломленным лучом и перпендикуляром к поверхности раздела двух сред в точке падения лучей, называют углом преломления.

Возникает вопрос: сколько энергии, принесенной излучением на поверхность раздела двух сред, унесут отраженные лучи и сколько — преломленные? Пусть излучение приносит в точку О за некоторое время энергию Дальше эта энергия разделяется: одну ее часть уносят отраженные, а другую — преломленные лучи. Из закона сохранения энергии следует, что

Поскольку всякая среда (кроме вакуума) поглощает энергию излучения, это равенство справедливо только при измерении энергии вблизи точки О. Если световое излучение проходит в среде значительные расстояния, мало ослабляясь, то среду называют прозрачной (например, стекло, воду, спирт и т. п.). Напротив, металлы очень сильно поглощают проникающее в них световое излучение, т. е. непрозрачны для него. Большую часть падающего на них излучения они отражают.

Вспомним, что морская вода и другие электролиты — хорошие проводники электрического тока, но слабо поглощают видимое излучение и этим резко отличаются от металлов. Это объясняется тем, что в электролитах нет свободных электронов, а ионы из-за своей сравнительно большой массы не успевают следовать высокочастотным колебаниям в световом луче.

Итак, каждая среда в той или иной степени отражает и поглощает световое излучение. Отражение и поглощение падающего на тело излучения зависят от рода вещества, от состояния поверхности, от состава излучения, от угла падения лучей и других причин. При увеличении угла падения лучей доля отраженного света увеличивается, а проникающего — уменьшается.

Заметим, что зависимость отражения и поглощения от частоты колебаний чаще всего имеет избирательный характер, т. е. колебания с одной частотой вещество отражает или поглощает сильно, а с другой — слабо. Например, атмосфера Земли сильно поглощает короткие волны видимого спектра и значительно слабее — его длинные волны. (Подумайте, почему в качестве сигнала об опасности используется красный свет, хотя наибольшая чувствительность глаза относится к зеленым лучам.)

Законы отражения света

С помощью опытов законы отражения для светового излучения были найдены еще в III в. до н. э. древнегреческим ученым Евклидом. В современных условиях проверка этих законов делается с помощью оптической шайбы (рис. 29.2). Она состоит из источника света А, который можно перемещать вокруг диска, разделенного на градусы. Направляя свет на отражающую поверхность 3, измеряют углы и

Законы отражения света совпадают с законами отражения волн от препятствий (§24.19).

1. Луч падающий и луч отраженный лежат в одной плоскости в перпендикуляром к отражающей поверхности, восставленным в точке падения луча.

2. Угол отражения луча равен углу его падения:

С помощью оптической шайбы можно показать, что падающий и отраженный лучи обратимы, т. е. если падающий луч направить по пути отраженного луча, то отраженный луч пойдет по пути падающего луча.

Законы отражения для сферического фронта волны. Покажем теперь, что они справедливы и для плоского фронта волны, т. е. для случая падения на плоскую поверхность параллельных лучей.

Пусть на гладкую поверхность КМ (рис. 29.3) падает плоская волна, фронт которой в какой-либо момент времени занимает положение A₁B₁. Через некоторое время он займет положение АС. В этот момент времени (мы примем его за нуль) от точки А начнет распространяться отраженная элементарная волна. Пока фронт волны за время t из точки С переместится в точку В, волна из точки А распространится по полусфере на расстояние AD, равное СВ, так как и ( — скорость распространения волн). Новым положением фронта волны после отражения лучей будет касательная к полусфере, проведенная из точки В, т. е. прямая BD. Дальше этот фронт волны будет двигаться параллельно самому себе по направлению лучей АА» или ВВ».

Поскольку прямоугольные треугольники ADB и АСВ имеют общую гипотенузу АВ и равные катеты AD и СВ, то они равны между собой. Поэтому Так как и как углы со взаимно перпендикулярными сторонами, то т. е. угол падения равен углу отражения, что и требовалось доказать.

Зеркальное и диффузное отражение. Плоское зеркало

Когда отражение света происходит от неровной поверхности, то ход отраженного луча в каждой ее точке определяется следующим образом. В точке падения луча проводится плоскость, касательная к поверхности, от которой происходит отражение, а затем строятся углы падения и отражения по отношению к этой плоскости.

Таким способом определены направления отраженных лучей в различных точках поверхности на рис. 29.4, где видно, что лучи, которые до отражения шли параллельным пучком, после отражения идут в разных направлениях. Такое отражение называют диффузным или рассеянным. Диффузное отражение света происходит от всех шероховатых поверхностей. Рассеянный свет, идущий от поверхностей различных тел, позволяет нам видеть эти тела.

Идеально гладкую поверхность, хорошо отражающую свет, называют зеркальной. Плоская зеркальная поверхность является плоским зеркалом (кроме плоских зеркал бывают сферические, параболические и т. д.). Пучок параллельных лучей после отражения от плоского зеркала остается параллельным, но изменяет направление своего распространения (рис. 29.5). Такое отражение называют зеркальным или правильным. На практике зеркальное отражение получается, если размеры неровностей на поверхности не превышают длины волны светового излучения.

Когда световые лучи от сильного источника света после отражения от плоского зеркала попадают в глаз человека, то они ослепляют его. Диффузное отражение неприятных ощущений в глазу не вызывает.

Если свет, рассеянный поверхностями различных тел, попадает на плоское зеркало, а затем, отражаясь, попадает в глаз человека, то в зеркале видны изображения этих тел. Выясним, как они возникают. Сначала рассмотрим, как получается изображение одной светящейся точки в плоском зеркале.

Пусть над поверхностью зеркала КМ (рис. 29.6) находится точечный источник света S. Луч SA, который идет от источника S по перпендикуляру к зеркалу, после отражения меняет свое направление на противоположное, т. е. идет по пути AS. Из всего множества лучей, попадающих из S на зеркало выделим луч SB, который падает на зеркало под углом i. После отражения он идет по пути BD, причем На рис. 29.6 видно, что лучи, падающие в точки А и В, после отражения идут так, как будто бы они вышли из одной точки S₁, расположенной симметрично точке S относительно зеркала КМ. Докажем это.

Угол равен углу поэтому и Поскольку , то и , т. е. Это означает, что прямоугольные треугольники SAB и S₁AB равны, так как имеют общий катет АВ и равные острые углы 1 и 2. Следовательно, SA =S₁A. Это равенство справедливо для всех лучей, падающих из точки S на зеркало.

Таким образом, когда человек смотрит в зеркало, то он видит изображение источника света S в точке S₁ хотя в действительности лучей, выходящих из точки S₁ и попадающих в глаз, не существует. Поэтому такое изображение принято называть мнимым. Если в точку S₁, где человек видит светящуюся точку, поместить экран, то на нем изображения точки S не получится. Это характерное Свойство мнимого изображения. Во всех других отношениях для наблюдателя мнимое изображение ничем не отличается от действительного.

Итак, в плоском зеркале получается мнимое изображение светящейся точки S, расположенное симметрично ей относительно зеркала в точке S₁.

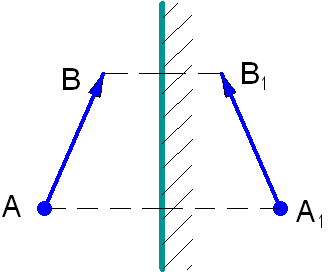
Представим теперь себе, что перед плоским зеркалом КМ находится предмет, который на рис. 29.7 условно изображен стрелкой BА. Положение изображения этого предмета в зеркале можно найти следующим образом. Опустив из крайних точек предмета перпендикуляры на зеркало и продолжив их за зеркало на расстояние, равное их длине до зеркала, получим точки A₁ и B₁ Соединив эти точки прямой линией, получим изображение стрелки ВА в зеркале. Это изображение будет мнимое и в натуральную величину. Оно имеет следующую особенность, отличающую его от других изображений: по сравнению с самим предметом левая и правая стороны у изображения в зеркале меняются местами. Такое изображение принято называть зеркальным.

Оказывается, что мнимыми бывают не только изображения, но и источники света. Пусть на пути лучей, которые должны сойтись в точке А (такие лучи можно получить с помощью линз), поместили плоское зеркало КМ (рис. 29.8). Тогда после отражения от зеркала лучи сойдутся в точке A₁ и затем уже пойдут расходящимся пучком, т. е. в точке A₁ получится действительное изображение источника света А, симметричное относительно зеркала КМ. Поскольку в точке А источника света в действительности нет, условились считать, что в ней находится мнимый источник света.

Итак, изображение действительного источника света в плоском зеркале получается мнимое и за зеркалом, а изображение мнимого источника света получается действительное и перед зеркалом.

Сферические зеркала

Зеркала, поверхности которых составляет часть поверхности шара, называют сферическими; они бывают вогнутые (рис. 29.9, а) и выпуклые (29.9, б). На рис. 29.9 R — радиус кривизны зеркала. Диаметр КМ окружности, ограничивающей зеркало, называют отверстием зеркала, а самую удаленную от него точку О зеркальной поверхности называют вершиной зеркала. Прямую, проходящую через сферический центр зеркала С и его вершину O, называют главной оптической осью зеркала, а любую другую прямую, проходящую через точку С и поверхность зеркала, называют побочной оптической осью зеркала.

Когда луч света идет по какой-либо оптической оси, то угол его падения на поверхность зеркала равен нулю, поэтому такой луч после отражения идет по той же оптической оси в обратную сторону.

Если на вогнутое зеркало падает пучок лучей, параллельных его главной оптической оси, то после отражения от зеркала эти лучи проходят через точку Ф, лежащую на главной оптической оси (рис. 29.10, а), которую называют главным фокусом зеркала. После отражения от выпуклого зеркала такие лучи идут расходящимся пучком (рис. 29.10, б), но так, что их продолжения тоже сходятся в одной точке Ф (за зеркалом) — главном фокусе зеркала.

Таким образом, вогнутые зеркала являются собирающими. Главный фокус у них действительный. Выпуклые зеркала — рассеивающие, главный фокус у них мнимый. Расстояние от главного фокуса до вершины зеркала ОФ называют главным фокусным расстоянием F.

Когда лучи падают на зеркало параллельно одной из его побочных оптических осей, например АС (рис. 29.11), то после отражения в фокусе зеркала. Если побочные оси составляют небольшой угол с главной оптической осью, то все фокусы зеркала располагаются в фокальной плоскости КМ, проходящей через главный фокус Ф перпендикулярно главной оптической оси.

Выясним, как связано главное фокусное расстояние F с радиусом кривизны зеркала R. Луч АА₁, параллельный главной оптической оси зеркала, после отражения идет по пути А₁Ф (рис. 29.10, а). Соединим точку А₁ со сферическим центром зеркала С. Из законов отражения следует, что Так как то Следовательно, и равнобедренный, т. е. Поскольку поверхность зеркала всегда составляет малую часть сферы, приближенно можно считать Таким образом, Это означает, что точка Ф делит радиус зеркала ОС пополам, т. е.

(29.1)

Из законов отражения следует, что падающий и отраженный лучи в сферических зеркалах обладают обратимостью. Поэтому, если источник света поместить в главный фокус вогнутого зеркала, то после отражения от зеркала лучи практически пойдут параллельно главной оптической оси зеркала (рис. 29.12).

Для получения параллельных пучков света на практике вместо сферического зеркала используют параболическое зеркало, отражающая поверхность которого является частью поверхности параболоида вращения *). Параболическое зеркало дает более направленный пучок света. На этом свойстве зеркал основано устройство прожекторов и рефлекторов (отражателей) различного рода.

*) Параболоид вращения — геометрическое тело, получающееся при вращении параболы вокруг ее оси симметрии.

Построение изображений, получаемых с помощью сферических зеркал. Формула сферического зеркала

Сферические зеркала могут давать различные изображения предметов. Для построения изображения одной точки А, создаваемого сферическим зеркалом, пользуются любыми двумя из трех лучей, показанных на рис. 29.13. Луч 1 из точки А проводится параллельно главной оптической оси. После отражения он проходит через главный фокус зеркала Ф. Луч 2 из точки А проводится через главный фокус Ф. После отражения от зеркала он идет параллельно главной оптической оси зеркала. Луч 3 проводится через сферический центр С зеркала. После отражения он идет обратно к точке А по той же прямой.

Примеры изображений предметов, создаваемых сферическими зеркалами, показаны на рис. 29.14. Заметим, что выпуклое зеркало всегда дает мнимое изображение предметов.

Выясним, как найти положение изображения светящейся точки А, расположенной на главной оптической оси ОС зеркала (рис. 29.15). Ясно, что изображение точки должно быть на этой же оси (объясните, почему).

Проведем из точки А произвольный луч АВ. В точку его падения В проведем радиус СВ. Он является нормалью (перпендикуляром) к поверхности зеркала, поэтому что и определяет положение отраженного луча BA₁. В точке А₁ и получится изображение точки А. Положение точки А₁ однозначно определяется положением самой точки А. Поэтому точки А и А₁ называют сопряженными.

Обозначим расстояние АО через d, А₁O — через f и ОС— через R. Для зеркал, поверхность которых составляет малую часть поверхности сферы, приближенно можно считать, что и Так как то линия ВС в треугольнике ABA₁ является биссектрисой угла ABA₁, а это означает, что отрезки АС и A₁C пропорциональны сторонам треугольника ABA₁:

или

Преобразуем последнее соотношение:

После деления на получим Заменяя R его значением из (29.1), получим формулу сопряженных точек зеркала:

(29.2)

Эта формула справедлива как для вогнутых, так и для выпуклых зеркал, но числовые значения действительных величин следует подставлять с плюсом, а мнимых — с минусом. Например, главное фокусное расстояние вогнутых зеркал берется со знаком плюс, а выпуклых — со знаком минус. Отрицательный ответ показывает, что соответствующая ему величина — мнимая.

Законы преломления света

Выше говорилось, что преломление света обусловлено изменением скорости распространения света при переходе излучения из одной среды в другую. Рассмотрим более подробно, как волновая теория объясняет преломление света.

Пусть на поверхность раздела двух прозрачных сред КМ (рис. 29.16) падает пучок параллельных лучей А’В’, фронт волны которых в начальный момент времени занимает положение АС. Если скорость распространения излучения в первой среде больше, чем скорость их распространения во второй среде, то за время t перемещения фронта волны на расстояние в первой среде, во второй среде волны распространяются из точки А по полусфере с радиусом Следовательно, фронт волны к этому моменту времени займет положение BD и дальше будет перемещаться параллельно самому себе в направлении АА» или ВВ».

Таким образом, при переходе из первой среды во вторую световые лучи преломляются так, что угол преломления оказывается меньше угла падения i, т. е. лучи приближаются к перпендикуляру AN.

Найдем математическую связь между углами i и . Из прямоугольного треугольника ABC имеем а из треугольника ABD имеем Разделив почленно эти равенства, получим Так как то

(29.3)

Поскольку отношение скоростей света для двух определенных сред есть величина постоянная, ее обозначают и называют показателем преломления второй среды относительно первой:

(29.4)

Из сопоставления формул (29.3) и (29.4) получаем

(29.5)

Справедливость формулы (29.5) можно проверить на опытах с оптической шайбой (рис. 29.17). При этом можно убедиться еще и в том, что падающий и преломленный лучи находятся в одной плоскости с отраженным лучом.

Итак, преломление света подчиняется двум законам.

1. Луч падающий и луч преломленный лежат в одной плоскости о перпендикуляром, восставленным в точке падения луча к поверхности раздела двух сред.

2. Отношение синуса угла падения к синусу угла преломления для двух данных сред есть величина постоянная:

Из второго закона следует, что при увеличении угла падения увеличивается и угол преломления (но не пропорционально).

Падающий и преломленный лучи обладают обратимостью, т. е. если падающий луч в первой среде, изображенный на рис. 29.18, а, направить по пути преломленного луча во второй среде, то после преломления он пойдет по пути падающего луча (рис. 29.18, 6). (Докажите это сами.) Следовательно, когда луч света переходит из среды оптически более плотной в среду оптически менее плотную, то он удаляется от перпендикуляра. Ясно, что числовое значение показателя преломления в этом случае будет меньше единицы.

Именно удалением световых лучей от перпендикуляра при преломлении объясняется кажущееся уменьшение глубины водоема, когда человек смотрит в воду (рис. 29.19, а). Если на дне водоема лежит камень К на глубине h, то человек видит мнимое изображение камня K₁ на глубине h₁. (Покажите, что где п — показатель преломления воды относительно воздуха.)

Когда человек смотрит в воду сбоку, то камень кажется смещенным еще и в горизонтальном направлении (к наблюдателю), так как человек видит мнимое изображение камня (рис. 29.19, б), положение которого зависит от угла падения лучей, попадающих в глаз.

Если лучи света падают на поверхность раздела прозрачных сред перпендикулярно к этой поверхности, то они проникают в другую среду, не преломляясь.

Абсолютный показатель преломления и его связь с относительным показателем преломления

Показатель преломления среды относительно вакуума, т. е. для случая перехода световых лучей из вакуума в среду, называется абсолютным (§ 27.7) и определяется формулой (27.10) :

При расчетах абсолютные показатели преломления берут из таблиц, поскольку их величина определена достаточно точно с помощью опытов. Так как с больше то абсолютный показатель преломления всегда больше единицы.

Если световое излучение переходит из вакуума в среду, то формулу второго закона преломления записывают в виде

(29.6)

Формулой (29.6) на практике часто пользуются и при переходе лучей из воздуха в среду, так как скорость распространения света в воздухе очень мало отличается от с. Это видно из того, что абсолютный показатель преломления воздуха равен 1,0029.

Когда луч идет из среды в вакуум (в воздух), то формула второго закона преломления принимает вид

(29.7)

В этом случае лучи при выходе из среды обязательно удаляются от перпендикуляра к поверхности раздела среды и вакуума.

Выясним, как можно найти относительный показатель преломления по абсолютным показателям преломления. Пусть свет переходит из среды с абсолютным показателем в среду с абсолютным показателем Тогда и откуда

(29.8)

Формулу второго закона преломления для такого случая часто записывают следующим образом:

(29.9)

Вспомним, что по теории Максвелла абсолютный показатель преломления можно найти из соотношения (27.11): Так как у веществ, прозрачных для светового излучения, практически равно единице, то можно считать, что

(29.10)

Поскольку частота колебаний в световом излучении имеет порядок 1014 Гц, ни диполи, ни ионы в диэлектрике, имеющие сравнительно большую массу, не успевают изменять своего положения с такой частотой, и диэлектрические свойства вещества в этих условиях определяются только электронной поляризацией его атомов (§ 15.10). Именно этим объясняется различие между значением из (29.10) и в электростатике. Так, у воды а у ионного твердого диэлектрика NaCl а Когда вещество состоит из однородных атомов или неполярных молекул, т. е. в нем нет ни ионов, ни природных диполей, то его поляризация может быть только электронной. Для подобных веществ из (29.10) и совпадают. Примером такого вещества является алмаз, состоящий только из атомов углерода.

Заметим, что величина абсолютного показателя преломления, кроме рода вещества, зависит еще от частоты колебаний, или от длины волны излучения. С уменьшением длины волны, как правило, показатель преломления увеличивается. Для стекла зависимость показателя преломления от длины волны приведена на рис. 34.3.

Полное отражение света. Предельный угол

Поместим источник света в какую-либо прозрачную среду и будем наблюдать переход светового излучения в среду оптически менее плотную, например в воздух (рис. 29.20).

На поверхности раздела свет будет и отражаться, и преломляться; по мере увеличения угла падения i энергия отраженного света будет возрастать, а энергия преломленного света — убывать. Кроме того, можно еще заметить, что при некотором угле падения i_п преломленный луч скользит по поверхности раздела сред, а при угле падения, большем i_п, преломленных лучей вообще нет. Явления такого рода можно обнаружить только в тех случаях, когда свет падает на поверхность раздела со стороны среды оптически более плотной, т. е. когда лучи при преломлении удаляются от перпендикуляра к поверхности раздела сред. Явление, при котором световое излучение полностью отражается от поверхности раздела прозрачных сред, называют полным отражением света.

Граница, отделяющая частично отраженные лучи от полностью отраженных лучей, определяется величиной угла i_п (рис. 29.20). Угол падения лучей i_п, при котором их угол преломления равен называют предельным углом падения. Заметим, что полное отражение происходит только у тех лучей, которые падают на поверхность раздела под углом i, большим предельного угла i_п. Величину предельного угла в каждом случае можно определить по относительному показателю преломления двух сред. Действительно, поскольку для угла i_п угол из формулы (29.9) имеем

Учитывая, что окончательно получим

(29.11)

Когда световое излучение переходит из какой-либо среды в вакуум (в воздух), отношение (29.11) принимает вид

(29.11а)

(Объясните, почему при переходе лучей из среды оптически менее плотной в среду более плотную полное отражение невозможно.)

Полая пробирка, опущенная в воду, и пузырьки газа в воде иногда блестят, как посеребренные. Это явление объясняется полным отражением лучей на границе жидкости или твердого тела с газообразной средой. Полное отражение света используется при устройстве светопроводящих волокон. Свет направляют внутрь прозрачного волокна через один торец, а выходит он через другой торец, многократно отражаясь от стенок волокна и следуя всем его изгибам.

Светопроводы используются для оптической связи. С помощью модуляции света, идущего по светопроводу, можно передавать по нему несравненно больший поток информации, чем по обычному высокочастотному кабелю.

По пучку светопроводящих волокон можно передавать изображение предмета, помещенного перед торцом пучка. Это используется в медицине для осмотра внутренних органов больного (при этом часть волокон используется для внутреннего освещения).

Прохождение света через пластинку с параллельными гранями и через трехгранную призму. Призма с полным отражением

Выясним, как изменяет ход световых лучей прозрачная пластинка с двумя плоскими и параллельными гранями. Примером такой пластинки является хорошее оконное стекло.

Пусть на пластинку, сделанную из вещества с показателем преломления n, падает из воздуха узкий пучок света AO₁ под углом i₁ (рис. 29.21). После преломления на верхней грани этот пучок идет внутри пластинки по пути O₁O₂, вторично преломляется на нижней грани и идет в воздухе по пути O₂B. Сравним углы i₁ и Для верхней грани формула второго закона преломления в данном случае принимает вид

а для нижней грани

Поскольку и равны, после почленного умножения этих равенств получим

откуда и означает, что луч AO₁ параллелен лучу О₂В. Следовательно, лучи света после прохождения через пластинку с плоскими и параллельными гранями смещаются параллельно самим себе. Расстояние, на которое смещается луч после прохождения пластинки, тем больше, чем толще пластинка и чем больше показатель преломления ее вещества. Кроме того, смещение d зависит от угла падения лучей i₁. Поэтому, когда человек смотрит сквозь толстую прозрачную пластинку под углом, все Предметы кажутся ему смещенными (рис. 29.22).

В прикладной оптике часто используют прозрачные трехгранные призмы. Две грани призмы, сквозь которые лучи входят в призму и выходят из нее, называют преломляющими гранями, а двугранный угол составленный этими гранями, называют преломляющим углом призмы.

Допустим, что на призму с показателем преломления n из воздуха падает узкий пучок света AO₁, какого-то определенного цвета (рис. 29.23, а). В призме он идет по пути O₁O₂. При выходе из призмы он удаляется от перпендикуляра к грани и идет по пути О₂В. Итак, в результате прохождения сквозь призму пучок света отклоняется к ее широкой части. Поскольку до призмы свет шел по направлению AO₁, а после призмы идет по направлению О₂В, то смещение пучка произошло на угол (рис. 29.23, а), который называют углом отклонения, Этот угол тем больше, чем больше показатель преломления вещества призмы n и ее преломляющий угол

Заметим, что поскольку показатель преломления n зависит от то и отклонение лучей в призме зависит от их цвета. Например, красные лучи отклоняются на меньший угол чем фиолетовые. Подробнее этот вопрос рассмотрим дальше (§ 34.2).

Если трехгранную призму поместить в такую среду, относительно которой показатель преломления вещества призмы окажется меньше единицы, то, пройдя призму, луч AO₁ (рис. 29.23, б) будет отклоняться в сторону преломляющего угла а не к широкой части призмы, на угол (Объясните, почему параллельные лучи, падающие на призму, после выхода из нее остаются параллельными.)

Подсчет показывает, что предельный угол для стекла составляет около 42. Поэтому в стеклянной прямоугольной призме с углами по 45° легко получить полное отражение света. На рис. 29.24, а показан поворот лучей на 90° в такой призме, а на рис. 29.24, б показано, как поворачивается изображение в такой же призме. На рис. 29.24, в изображена призма прямого зрения и ход лучей в ней. Видно, что верхние и нижние лучи меняются местами, но продолжают распространяться в прежнем направлении.

Услуги по физике:

Лекции по физике:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

📹 Видео

Урок 202 (осн). Преломление света. Законы преломленияСкачать

Отражение света. Законы отражения света | Физика 8 класс #27 | ИнфоурокСкачать

8 класс. Решение задач на преломление света.Скачать

Законы отражения света. Плоское зеркало.Скачать

Поляризация отраженного светаСкачать

Урок 199 (осн). Задачи на законы отраженияСкачать

Отражение света, законы отражения, плоские зеркала. Практическая часть - решение задачи. 8 класс.Скачать

Отражение света от плоского зеркалаСкачать

Урок 203 (осн). Задачи на законы преломления - 1Скачать

ПРЕЛОМЛЕНИЕ СВЕТА закон 8 класс физика ПерышкинСкачать

Преломление света, закон преломления света, полное внутреннее отражение. 8 класс.Скачать

Урок 381. Принцип Гюйгенса. Вывод законов отражения и преломления волнСкачать

Урок 423. Поляризация света. Закон МалюсаСкачать

Физика 11 класс (Урок№12 - Световые волны.)Скачать