Уравнение отрезка в трехмерном пространстве

Эта статья является продолжением темы прямая в пространстве. Здесь мы от геометрического описания прямой линии в пространстве перейдем к алгебраическому описанию, то есть, определим прямую с помощью уравнений в фиксированной прямоугольной системе координат Oxyz в трехмерном пространстве.

Статья построена следующим образом: сначала приведена общая информация, которая раскрывает значение фразы «уравнения прямой в пространстве», после этого рассмотрены уравнения прямой в пространстве различного вида, показана связь между ними и приведены примеры уравнений прямой.

Навигация по странице.

Видео:11. Прямая в пространстве и ее уравненияСкачать

Уравнения прямой в пространстве – начальные сведения.

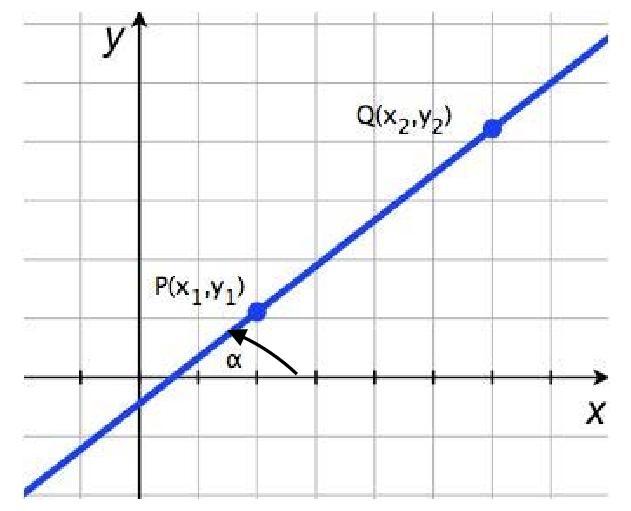
Уравнение прямой на плоскости в прямоугольной системе координат Oxy представляет собой линейное уравнение с двумя переменными x и y , которому удовлетворяют координаты любой точки прямой и не удовлетворяют координаты никаких других точек. С прямой в трехмерном пространстве дело обстоит немного иначе – не существует линейного уравнения с тремя переменными x , y и z , которому бы удовлетворяли только координаты точек прямой, заданной в прямоугольной системе координат Oxyz . Действительно, уравнение вида , где x , y и z – переменные, а A , B , C и D – некоторые действительные числа, причем А , В и С одновременно не равны нулю, представляет собой общее уравнение плоскости. Тогда встает вопрос: «Каким же образом можно описать прямую линию в прямоугольной системе координат Oxyz »?

Ответ на него содержится в следующих пунктах статьи.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнения прямой в пространстве — это уравнения двух пересекающихся плоскостей.

Напомним одну аксиому: если две плоскости в пространстве имеют общую точку, то они имеют общую прямую, на которой находятся все общие точки этих плоскостей. Таким образом, прямую линию в пространстве можно задать, указав две плоскости, пересекающиеся по этой прямой.

Переведем последнее утверждение на язык алгебры.

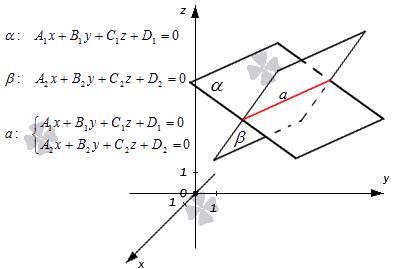
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz и известно, что прямая a является линией пересечения двух плоскостей и , которым отвечают общие уравнения плоскости вида и соответственно. Так как прямая a представляет собой множество всех общих точек плоскостей и , то координаты любой точки прямой a будут удовлетворять одновременно и уравнению и уравнению , координаты никаких других точек не будут удовлетворять одновременно обоим уравнениям плоскостей. Следовательно, координаты любой точки прямой a в прямоугольной системе координат Oxyz представляют собой частное решение системы линейных уравнений вида , а общее решение системы уравнений определяет координаты каждой точки прямой a , то есть, определяет прямую a .

Итак, прямая в пространстве в прямоугольной системе координат Oxyz может быть задана системой из уравнений двух пересекающихся плоскостей .

Вот пример задания прямой линии в пространстве с помощью системы двух уравнений — .

Рекомендуем продолжить изучение этой темы, обратившись к статье уравнения прямой в пространстве — уравнения двух пересекающихся плоскостей. В ней дана более детальная информация, подробно разобраны решения характерных примеров и задач, а также показан способ перехода к уравнениям прямой в пространстве другого вида.

Следует отметить, что существуют различные способы задания прямой в пространстве, и на практике прямая чаще задается не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, лежащей на этой прямой. В этих случаях проще получить канонические и параметрические уравнения прямой в пространстве. О них поговорим в следующих пунктах.

Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Параметрические уравнения прямой в пространстве.

Параметрические уравнения прямой в пространстве имеют вид , где x₁ , y₁ и z₁ – координаты некоторой точки прямой, a_x , a_y и a_z ( a_x , a_y и a_z одновременно не равны нулю) — соответствующие координаты направляющего вектора прямой, а — некоторый параметр, который может принимать любые действительные значения.

При любом значении параметра по параметрическим уравнениям прямой в пространстве мы можем вычислить тройку чисел , она будет соответствовать некоторой точке прямой (отсюда и название этого вида уравнений прямой). К примеру, при из параметрических уравнений прямой в пространстве получаем координаты x₁ , y₁ и z₁ : .

В качестве примера рассмотрим прямую, которую задают параметрические уравнения вида . Эта прямая проходит через точку , а направляющий вектор этой прямой имеет координаты .

Рекомендуем продолжить изучение темы, обратившись к материалу статьи параметрические уравнения прямой в пространстве. В ней показан вывод параметрических уравнений прямой в пространстве, разобраны частные случаи параметрических уравнений прямой в пространстве, даны графические иллюстрации, приведены развернутые решения характерных задач и указана связь параметрических уравнений прямой с другими видами уравнений прямой.

Видео:Уравнение прямой в пространстве. 11 класс.Скачать

Канонические уравнения прямой в пространстве.

Разрешив каждое из параметрических уравнений прямой вида относительно параметра , легко перейти к каноническим уравнениям прямой в пространстве вида .

Канонические уравнения прямой в пространстве определяют прямую, проходящую через точку , а направляющим вектором прямой является вектор . К примеру, уравнения прямой в каноническом виде соответствуют прямой, проходящей через точку пространства с координатами , направляющий вектор этой прямой имеет координаты .

Следует отметить, что одно или два из чисел в канонических уравнениях прямой могут быть равны нулю (все три числа одновременно не могут быть равны нулю, так как направляющий вектор прямой не может быть нулевым). Тогда запись вида считается формальной (так как в знаменателях одной или двух дробей будут нули) и ее следует понимать как , где .

Если одно из чисел в канонических уравнениях прямой равно нулю, то прямая лежит в одной из координатных плоскостей, либо в плоскости ей параллельной. Если два из чисел равны нулю, то прямая либо совпадает с одной из координатных осей, либо параллельна ей. Например прямая, соответствующая каноническим уравнениям прямой в пространстве вида , лежит в плоскости z=-2 , которая параллельна координатной плоскости Oxy , а координатная ось Oy определяется каноническими уравнениями .

Графические иллюстрации этих случаев, вывод канонических уравнений прямой в пространстве, подробные решения характерных примеров и задач, а также переход от канонических уравнений прямой к другим уравнениям прямой в пространстве смотрите в статье канонические уравнения прямой в пространстве.

Видео:§51 Уравнение прямой в пространстве, проходящей через две точкиСкачать

Способы задавания уравнений прямых в плоскости и в трехмерном пространстве

Прямая является основным геометрическим объектом на плоскости и в трехмерном пространстве. Именно из прямых строятся многие фигуры, например: параллелограмм, треугольник, призма, пирамида и так далее. Рассмотрим в статье различные способы задавания уравнений прямых.

Видео:Написать канонические и параметрические уравнения прямой в пространствеСкачать

Определение прямой и виды уравнений для ее описания

Каждый школьник хорошо себе представляет, о каком геометрическом объекте идет речь. Прямую можно представить как совокупность точек, причем если соединить каждую из них по очереди со всеми остальными, то мы получим набор параллельных векторов. Иными словами, попасть в каждую точку прямой можно из одной фиксированной ее точки, перенося ее на некоторый единичный вектор, умноженный на действительное число. Это определение прямой используется для задавания векторного равенства для ее математического описания как на плоскости, так и в трехмерном пространстве.

Вам будет интересно: Муляж — это необходимость или выдумка?

Прямая может быть математически представлена следующими видами уравнений:

• общее;
• векторное;
• параметрическое;
• в отрезках;
• симметричное (каноническое).

Далее рассмотрим все названные виды и покажем на примерах решения задач, как с ними работать.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Векторное и параметрическое описание прямой

Вам будет интересно: Размер бумаги А3 в сантиметрах и не только: краткий путеводитель

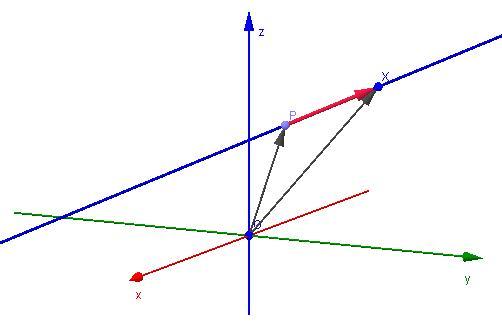
Начнем с задавания прямой через известный вектор. Предположим, что в пространстве имеется фиксированная точка M(x0; y0; z0). Известно, что прямая проходит через нее и направлена вдоль векторного отрезка v¯(a; b; c). Как по этим данным найти произвольную точку прямой? Ответ на этот вопрос даст следующее равенство:

(x; y; z) = (x0; y0; z0) + λ * (a; b; c)

Где λ — произвольное число.

Аналогичное выражение можно записать для двумерного случая, где координаты векторов и точек представлены набором из двух чисел:

(x; y) = (x0; y0) + λ * (a; b)

Записанные уравнения называются векторными, а сам направленный отрезок v¯ — это направляющий вектор для прямой.

Из записанных выражений соответствующие параметрические уравнения получаются просто, достаточно лишь переписать их в явном виде. Например, для случая в пространстве получаем следующее уравнение:

С параметрическими уравнениями удобно работать, если необходимо проанализировать поведение каждой координаты. Заметим, что хотя параметр λ может принимать произвольные значения, но во всех трех равенствах он должен быть одинаковым.

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Общее уравнение

Другим способом задавания прямой, который часто используют для работы с рассматриваемым геометрическим объектом, является применение уравнения общего вида. Для двумерного случая оно имеет вид:

A * x + B * y + C = 0

Здесь большие латинские буквы представляют конкретные числовые значения. Удобство данного равенства при решении задач заключается в том, что оно в явном виде содержит вектор, который перпендикулярен прямой. Если обозначить его n¯, тогда можно записать:

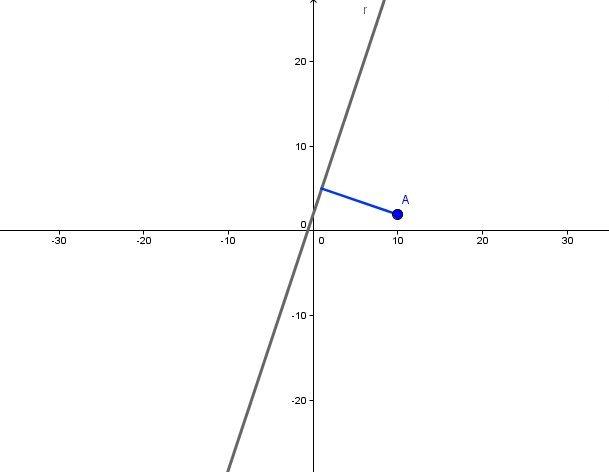
Кроме того, выражение удобно применять для определения расстояния от прямой до некоторой точки P(x1; y1). Формула для расстояния d имеет вид:

d = |A * x1 + B * y1 + C| / √(A2 + B2)

Несложно показать, что если из общего уравнения выразить явно переменную y, то получится следующая известная форма записи прямой:

Где k и b однозначно определяются числами A, B, C.

Видео:12. Уравнения прямой в пространстве Решение задачСкачать

Уравнение в отрезках и каноническое

Уравнение в отрезках проще всего получить из общего вида. Покажем, как это можно сделать.

Предположим, что имеется следующая прямая:

A * x + B * y + C = 0

Перенесем свободный член в правую часть равенства, затем поделим на него все уравнение, получаем:

x / (-C / A) + y / (-C / B) = 1;

x / q + y / p = 1, где q = -C / A, p = -C / B

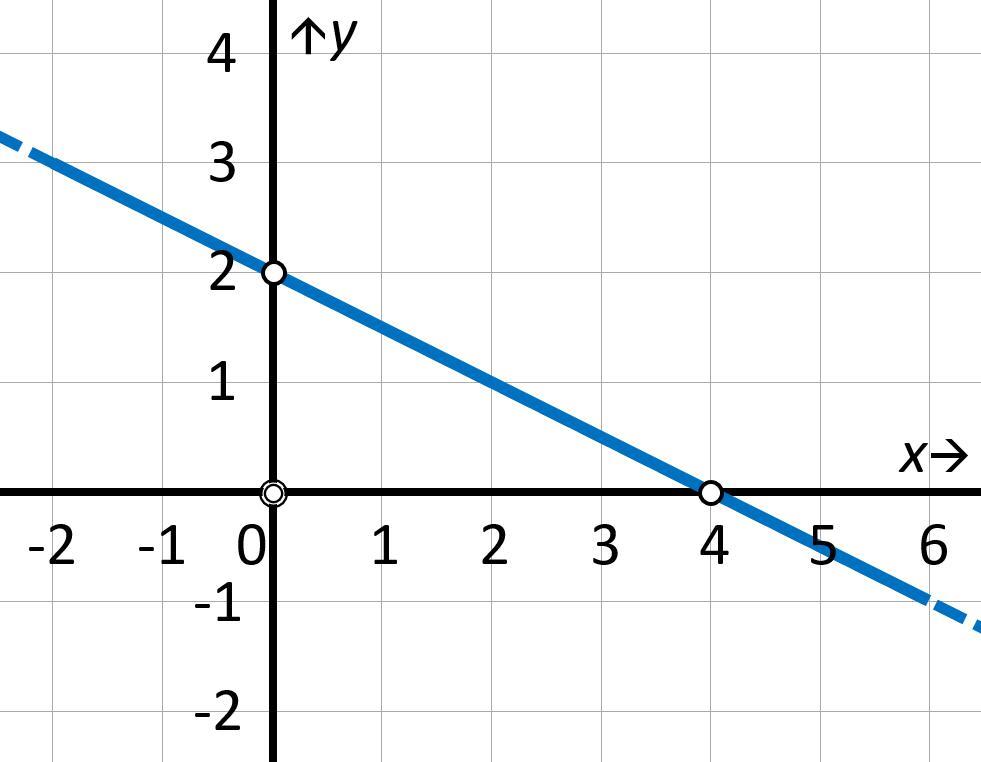
Мы получили так называемое уравнение в отрезках. Свое название оно получило по причине того, что знаменатель, на который делится каждая переменная, показывает значение координаты пересечения прямой с соответствующей осью. Этот факт удобно использовать для изображения прямой в координатной системе, а также для анализа ее взаимного расположения по отношению к другим геометрическим объектам (прямым, точкам).

Теперь перейдем к получению канонического уравнения. Это проще сделать, если рассмотреть параметрический вариант. Для случая на плоскости имеем:

Выразим параметр λ в каждом равенстве, затем приравняем их, получаем:

(x — x0) / a = (y — y0) / b

Это и есть искомое уравнение, записанное в симметричной форме. Так же, как и векторное выражение, оно в явной форме содержит координаты направляющего вектора и координаты одной из точек, которая принадлежит прямой.

Можно заметить, что в данном пункте мы привели уравнения для двумерного случая. Аналогичным образом можно составить уравнение прямой в пространстве. Здесь нужно заметить, что если каноническая форма записи и выражение в отрезках будут иметь такой же вид, то общее уравнение в пространстве для прямой представляется системой из двух уравнений для пересекающихся плоскостей.

Видео:Видеоурок "Канонические уравнения прямой"Скачать

Задача на построение уравнения прямой

Из геометрии каждый школьник знает, что через две точки можно начертить единственную линию. Предположим, что в координатной плоскости заданы следующие точки:

Следует найти уравнение прямой, которой принадлежат обе точки, в отрезках, в векторном, каноническом и в общем виде.

Получим сначала векторное уравнение. Для этого следует определить для прямой направляющий вектор M1M2¯:

M1M2¯ = (-1; 3) — (1; 2) = (-2; 1)

Теперь можно составить векторное уравнение, взяв одну из двух заданных в условии задачи точек, например, M2:

(x; y) = (-1; 3) + λ * (-2; 1)

Чтобы получить каноническое уравнение, достаточно преобразовать найденное равенство в параметрический вид и исключить параметр λ. Имеем:

x = -1 — 2 * λ, следовательно, λ = x + 1 / (-2);

y = 3 + λ, далее получаем λ = y — 3;

x + 1 / (-2) = (y — 3) / 1

Оставшиеся два уравнения (общее и в отрезках) можно найти из канонического, преобразуя его следующим образом:

общее уравнение: x + 2 * y — 5 = 0;

в отрезках уравнение: x / 5 + y / 2,5 = 1

Полученные уравнения показывают, что вектор (1; 2) должен быть перпендикулярен прямой. Действительно, если найти его скалярное произведение с направляющим вектором, то оно будет равно нулю. Уравнение в отрезках говорит, что прямая пересекает ось x в точке (5; 0), а ось y — в точке (2,5; 0).

Видео:Видеоурок "Параметрические уравнения прямой"Скачать

Задача на определение точки пересечения прямых

На плоскости заданы две прямые следующими уравнениями:

(x; y) = (0; -1) + λ * (-1; 3)

Необходимо определить координаты точки, в которой эти прямые пересекаются.

Решить задачу можно двумя способами:

Не выполнять никаких преобразований, а просто подставить координату точки пересечения, выраженную через параметр λ, в первое уравнение. Затем найти значение параметра.

Поступим вторым способом. Имеем:

2 * (-λ) + (-1) + 3 * λ — 1 = 0;

Подставляем полученное число в векторное уравнение:

(x; y) = (0; -1) + 2 * (-1; 3) = (-2; 5)

Таким образом, единственной точкой, которая принадлежит обеим прямым, является точка с координатами (-2; 5). В ней прямые пересекаются.

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Уравнения прямой, виды уравнений прямой в пространстве

Материал этой статьи продолжает тему прямой в пространстве. От геометрического описания пойдем к алгебраическому: зададим прямую при помощи уравнений в фиксированной прямоугольной системе координат трехмерного пространства. Приведем общую информацию, расскажем о видах уравнений прямой в пространстве и их связи между собой.

Видео:Длина отрезкаСкачать

Уравнение прямой в пространстве: общие сведения

Уравнение прямой на плоскости в прямоугольной системе координат O x y – это линейное уравнение с переменными x и y , которому отвечают координаты всех точек прямой и не удовлетворяют координаты никаких прочих точек.

Если речь идет о прямой в трехмерном пространстве, все несколько иначе: не существует такого линейного уравнения с тремя переменными x , y , z , которому бы отвечали только координаты точек заданной прямой. В самом деле, уравнение A x + B y + C z + D = 0 , где x , y , z – переменные, а А , В , С и D – некоторые действительные числа ( А , В , С одновременно не равны нулю) – это общее уравнение плоскости. Тогда как же задать прямую линию в прямоугольной системе координат O x y z ? Найдем ответ на этот вопрос в следующих пунктах темы.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнение прямой в пространстве как уравнение двух пересекающихся плоскостей

Когда две плоскости в пространстве имеют общую точку, существует их общая прямая, на которой находятся все общие точки этих плоскостей.

Рассмотрим это утверждение в алгебраическом толковании.

Допустим, в трехмерном пространстве зафиксирована прямоугольная система координат O x y z и задано, что прямая a – это линия пересечения двух плоскостей α и β , которые соответственно описываются уравнениями плоскости A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 . Поскольку прямая a – это множество общих точек плоскостей α и β , то координаты любой точки прямой a будут одновременно отвечать обоим уравнениям. Никакие прочие точки одновременно удовлетворять условия обоих уравнений не будут.

Таким образом, координаты любой точки прямой a в прямоугольной системе координат станут частным решением системы линейных уравнений вида

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0

Общее же решение системы уравнений _ A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 определит координаты каждой точки прямой a , т.е. по сути задает саму прямую a .

Резюмируем: прямая в пространстве в прямоугольной системе координат O x y z может быть задана системой уравнений двух плоскостей, которые пересекаются:

A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0

Приведем пример описания прямой линии в пространстве при помощи системы уравнений:

x + 3 y — 2 1 z + 11 3 y + 1 4 z — 2 = 0

Навык определения прямой линии уравнениями пересекающихся плоскостей необходим при решении задач на нахождение координат точки пересечения прямой и плоскости или нахождение координат точки пересечения двух прямых в пространстве.

Подробнее изучить эту тему можно, обратившись к статье об уравнениях прямой в пространстве, уравнениях двух пересекающихся прямых.

Заметим, что существует несколько способов описания прямой в пространстве. В практике прямую чаще задают не двумя пересекающимися плоскостями, а направляющим вектором прямой и точкой, принадлежащей этой прямой. В подобных случаях легче задать канонические и параметрические уравнения прямой в пространстве. Поговорим о них ниже.

Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

Параметрические уравнения прямой в пространстве

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , где x 1 , y 1 , z 1 – координаты некой точки прямой; а x , а y и a z (одновременно не равны нулю) – координаты направляющего вектора прямой. а · λ – некий параметр, принимающий любые действительные значения.

Любое значение параметра λ позволяет, используя параметрические уравнения прямой в пространстве, определить тройку чисел ( x , y , z ) , соответствующую некой точке прямой (отсюда и название такого вида уравнений). Например, пусть λ = 0 , тогда из параметрических уравнений прямой в пространстве получим координаты:

x = x 1 + a x · 0 y = y 1 + a y · 0 z = z 1 + a z · 0 ⇔ x = x 1 y = y 1 z = z 1

Рассмотрим конкретный пример:

Пусть прямая задана параметрическими уравнениями вида x = 3 + 2 · a x y = — 2 · a y z = 2 + 2 · a z .

Заданная прямая проходит через точку М 1 ( 3 , 0 , 2 ) ; направляющий вектор этой прямой имеет координаты 2 , — 2 , 2 .

Продолжение изучения этой темы можно найти в статье о параметрических уравнениях прямой в пространстве.

Видео:Видеоурок "Уравнение прямой в отрезках"Скачать

Канонические уравнения прямой в пространстве

Если разрешить каждое из параметрических уравнений прямой

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ относительно параметра λ , возможно просто перейти к каноническим уравнениям прямой в пространстве x — x 1 a x = y — y 1 a y = z — z 1 a z .

Канонические уравнения прямой в пространстве задают прямую, которая проходит через точку М 1 ( x 1 , y 1 , z 1 ) , и у которой направляющий вектор равен a → = ( a x , a y , a z ) . Например, задана прямая, описываемая каноническим уравнением x — 1 1 = y 2 = z + 5 7 . Эта прямая проходит через точку с координатами ( 1 , 0 , — 5 ) , ее направляющий вектор имеет координаты ( 1 , 2 , — 7 ) .

Отметим, что одно или два числа из чисел а x , а y и а z в канонических уравнениях прямой могут быть равны нулю (все три числа не могут быть равны нулю, поскольку направляющий вектор не может быть нулевым). В таком случае запись вида x — x 1 a x = y — y 1 a y = z — z 1 a z является формальной (поскольку в знаменателях одной или двух дробей будут нули) и понимать ее нужно как:

x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , где λ ∈ R .

Если одно из чисел а x , а y и a z канонического уравнения прямой равно нулю, то прямая лежит в какой-то из координатных плоскостей, или в плоскости, ей параллельной. Если два из чисел а x , а y и a z равны нулю, то прямая или совпадает с какой-либо из координатных осей, или параллельна ей. К примеру, прямая, описываемая каноническим уравнением x + 4 3 = y — 5 2 = z + 2 0 , лежит в плоскости z = — 2 , параллельной координатной плоскости O x y , а координатная ось O y описывается каноническими уравнениями x 0 = y 1 = z 0 .

Графические иллюстрации подобных случаев, составление канонических уравнений прямой в пространстве, примеры решения типовых задач, а также алгоритм перехода от канонических уравнений к другим видам уравнений прямой в пространстве рассмотрены в статье о канонических уравнениях прямой в пространстве.

🌟 Видео

10. Параллельность и перпендикулярность плоскостей Решение задачСкачать

Уравнения стороны треугольника и медианыСкачать

Лекция 28. Виды уравнения прямой в пространстве.Скачать