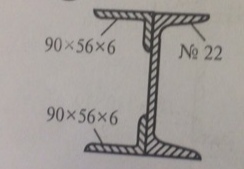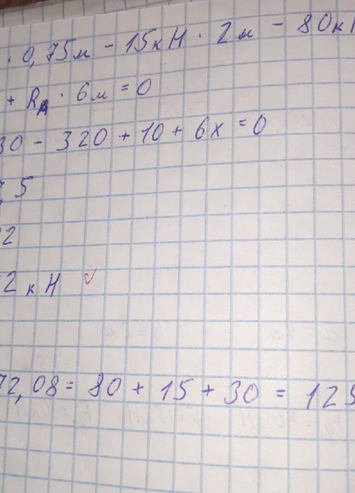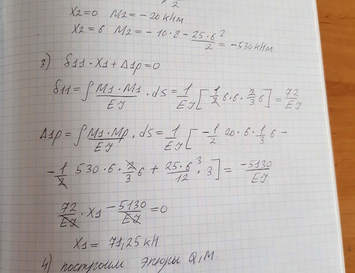Виды выражений
Решение
Дано ур-ние линии 2-порядка:
$$36 x^ — 36 x + 36 y^ — 24 y — 23 = 0$$
Это уравнение имеет вид:
$$a_ x^ + 2 a_ x y + 2 a_ x + a_ y^ + 2 a_ y + a_ = 0$$
где
$$a_ = 36$$
$$a_ = 0$$
$$a_ = -18$$
$$a_ = 36$$
$$a_ = -12$$
$$a_ = -23$$
Вычислим определитель
$$Delta = left|begina_ & a_\a_ & a_endright|$$
или, подставляем
$$Delta = left|begin36 & 0\0 & 36endright|$$
$$Delta = 1296$$
Т.к.
$$Delta$$
не равен 0, то
находим центр канонической системы координат. Для этого решаем систему уравнений
$$a_ x_ + a_ y_ + a_ = 0$$
$$a_ x_ + a_ y_ + a_ = 0$$
подставляем коэффициенты
$$36 x_ — 18 = 0$$
$$36 y_ — 12 = 0$$
тогда
$$x_ = frac$$
$$y_ = frac$$
Тем самым мы перешли к уравнению в системе координат O’x’y’
$$a’_ + a_ x’^ + 2 a_ x’ y’ + a_ y’^ = 0$$
где
$$a’_ = a_ x_ + a_ y_ + a_$$
или
$$a’_ = — 18 x_ — 12 y_ — 23$$
$$a’_ = -36$$
тогда ур-ние превратится в
$$36 x’^ + 36 y’^ — 36 = 0$$
Данное уравнение является окружностью
$$frac<tilde x^><1^> + frac<tilde y^><1^> = 1$$
— приведено к каноническому виду
Центр канонической системы координат в точке O
Базис канонической системы координат
$$vec e_1 = left ( 1, quad 0right )$$
$$vec e_2 = left ( 0, quad 1right )$$
Дано ур-ние линии 2-порядка:
$$36 x^ — 36 x + 36 y^ — 24 y — 23 = 0$$
Это уравнение имеет вид:
$$a_ x^ + 2 a_ x y + 2 a_ x + a_ y^ + 2 a_ y + a_ = 0$$
где
$$a_ = 36$$
$$a_ = 0$$
$$a_ = -18$$
$$a_ = 36$$
$$a_ = -12$$
$$a_ = -23$$
Инвариантами данного уравнения при преобразовании координат являются определители:
$$I_ = a_ + a_$$
подставляем коэффициенты
$$I_ = 72$$
$$I_ = left|begin36 & 0 & -18\0 & 36 & -12\-18 & -12 & -23endright|$$
$$I = left|begin- lambda + 36 & 0\0 & — lambda + 36endright|$$
© Контрольная работа РУ — калькуляторы онлайн
Видео:Лекция 23. Виды уравнений прямой на плоскости.Скачать
Где учитесь?
Для правильного составления решения, укажите:
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать
Неравенства
Решение неравенств онлайн
Перед тем как решать неравенства, необходимо хорошо усвоить как решаются уравнения.
Не важно каким является неравенство – строгим ( ) или нестрогим (≤, ≥), первым делом приступают к решению уравнения, заменив знак неравенства на равенство (=).
Поясним что означает решить неравенство?
После изучения уравнений в голове у школьника складывается следующая картина: нужно найти такие значения переменной, при которых обе части уравнения принимают одинаковые значения. Другими словами, найти все точки, в которых выполняется равенство. Всё правильно!
Когда говорят о неравенствах, имеют в виду нахождение интервалов (отрезков), на которых выполняется неравенство. Если в неравенстве две переменные, то решением будут уже не интервалы, а какие-то площади на плоскости. Догадайтесь сами, что будет решением неравенства от трех переменных?
Как решать неравенства?
Универсальным способом решения неравенств считают метод интервалов (он же метод промежутков), который заключается в определении всех интервалов, в границах которых будет выполняться заданное неравенство.
Не вдаваясь в тип неравенства, в данном случае это не суть, требуется решить соответствующее уравнение и определить его корни с последующим обозначением этих решений на числовой оси.
Можно сказать на этом полдела сделано. Далее, взяв любую точку на каждом интервале, осталось определить выполняется ли само неравенство? Если выполняется, то он входит в решение неравенства. Ели нет, то пропускаем его.
Как правильно записывать решение неравенства?
Когда вы определили интервалы решений неравенства, нужно грамотно выписать само решение. Есть важный нюанс – входят ли границы интервалов в решение?
Тут всё просто. Если решение уравнения удовлетворяет ОДЗ и неравенство является нестрогим, то граница интервала входит в решение неравенства. В противном случае – нет.
Рассматривая каждый интервал, решением неравенства может оказаться сам интервал, либо полуинтервал (когда одна из его границ удовлетворяет неравенству), либо отрезок – интервал вместе с его границами.
Не думайте, что решением неравенства могут быть только интервалы, полуинтервалы и отрезки. Нет, в решение могут входить и отдельно взятые точки.
Например, у неравенства |x|≤0 всего одно решение – это точка 0.
Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать
Материалы для скачивания
Рейтинг ↑ не забываем
Порядок действий при демонтаже кондиционеров (посмотреть)
Свод правил вентиляции и кондиционирования 2017 год (посмотреть)
Условные обозначения систем вентиляции и кондиционирования (посмотреть)
Требования к пожарной безопастности по вентиляции и кондиционированию (посмотреть).
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Ответы на задачи по технической механике
Если Вы не нашли свой вариант ответа, обращайтесь перейдя по ссылке в группу ВК опубликовав Ваши задачи прям в ленту группы ,по возможности постараемся Вам помочь. На данной странице не все ответы, перейдя по ссылке попадаете на другую страницу с ответами
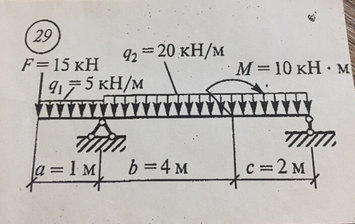
Задача № 29 Найти реакцию опор
Ответ к задачи №29
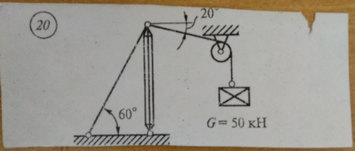
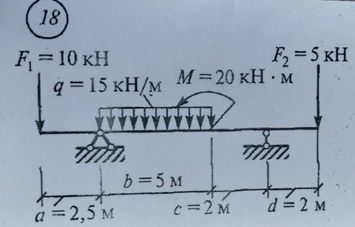
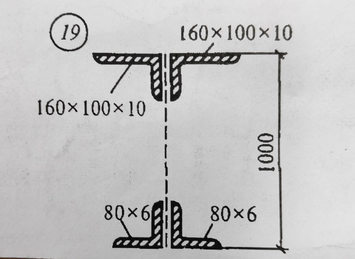
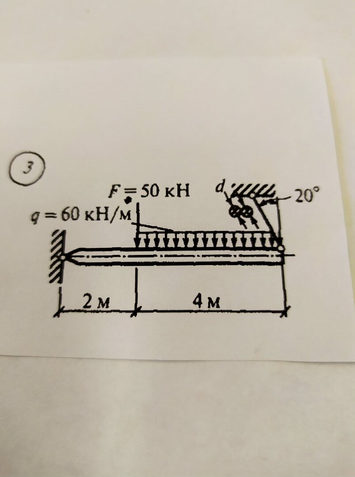
Задача № 20 Натяжка троса
Ответ к задачи № 20
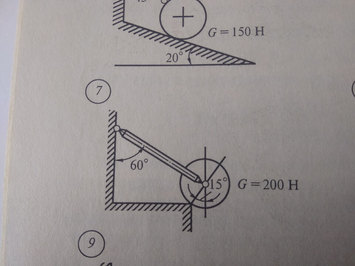
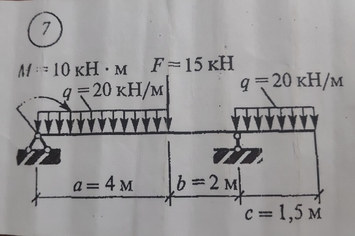
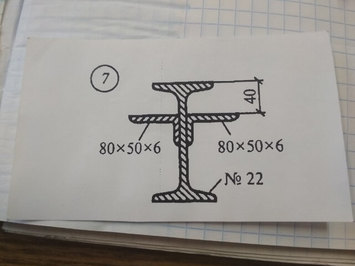
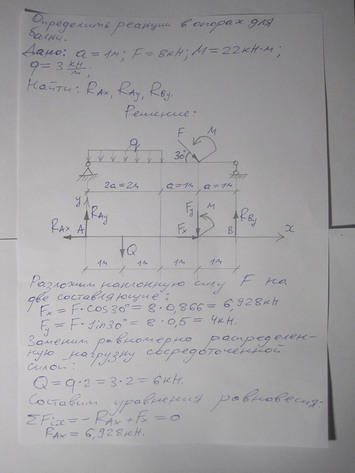
Задача №7 Найти реакцию опор
Ответ к задаче №7
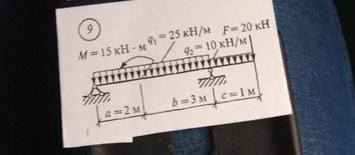
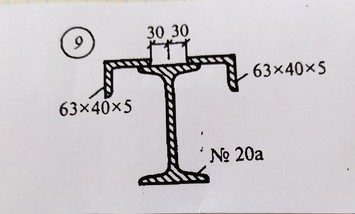
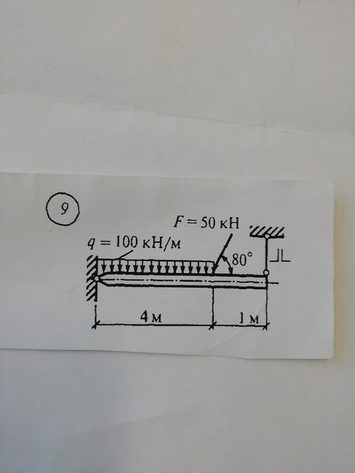
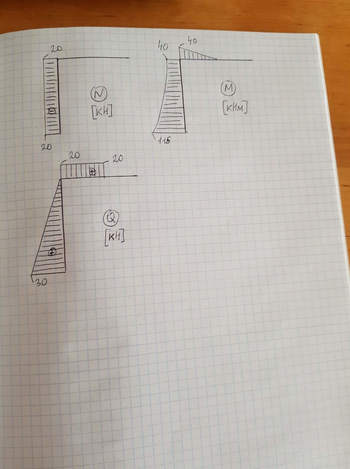
Задача № 9 Распределение нагрузки
Ответ к задачи № 9
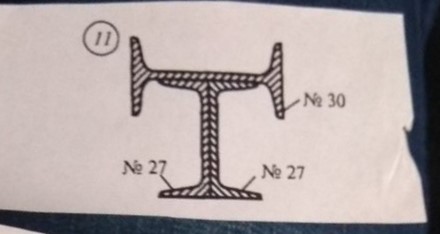
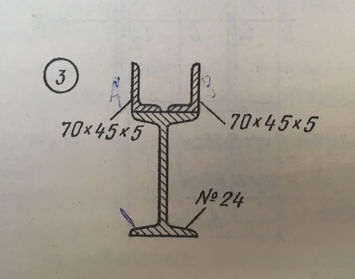
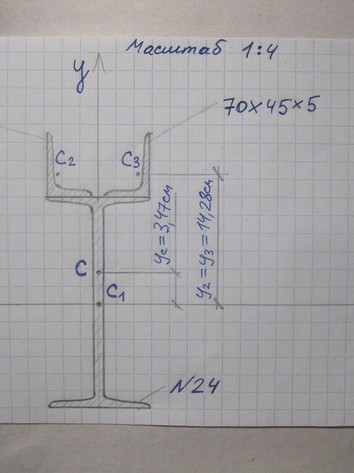
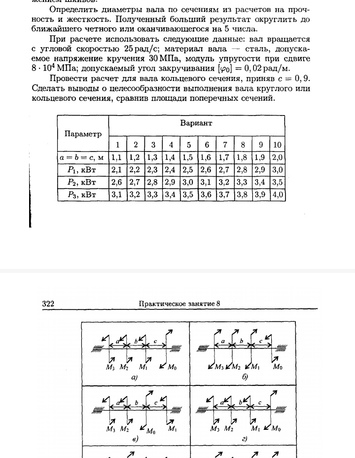
Задача № 11 Определить координаты центра тяжести сечения
Ответ к задачи № 11 С решением
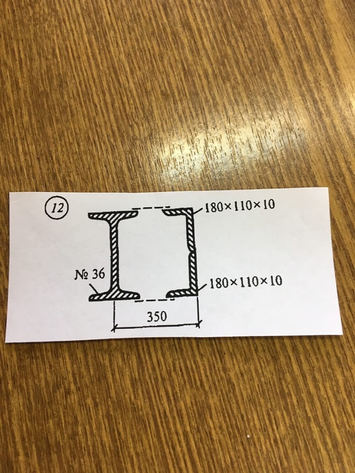
Задача № 12 Найти реакцию опор
Ответ к задачи №12
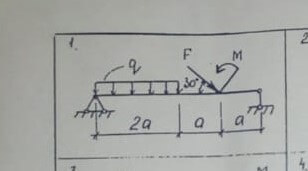
Задача № 13 Решить графически
Ответ к задаче №13
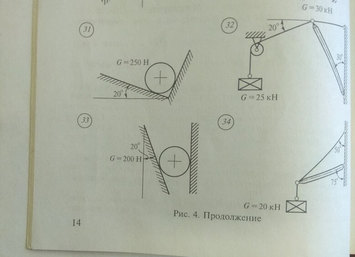
Задача № 33 Решить графически
Ответ к задачи № 33
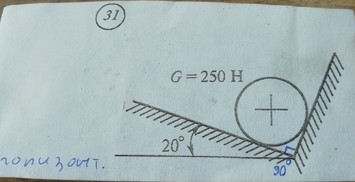
Задача № 33 Силы давящие на шар
Ответ к задачи № 33 Силы давящие на шар
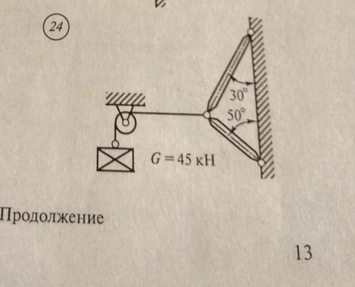
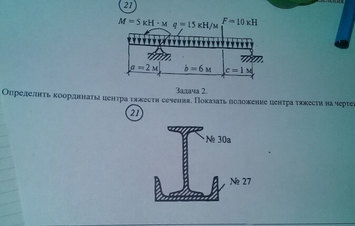
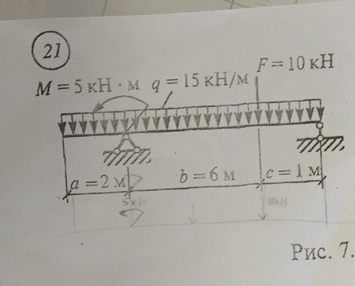
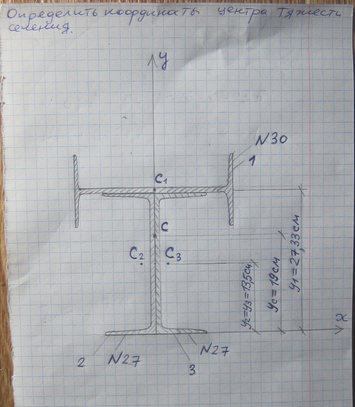
Задача № Задача №21 Определить координат центра тяжести
Ответ к задаче № 21 Определить координат центра тяжести
Ответ № 21 /2 Определить координат центра тяжести 30А Ответ на координат центр тяжести № 21 -27
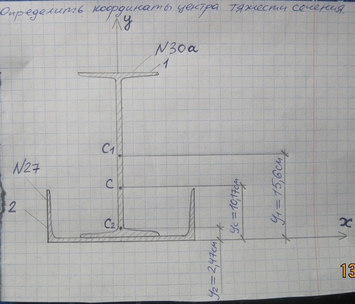
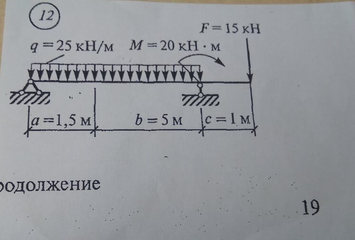
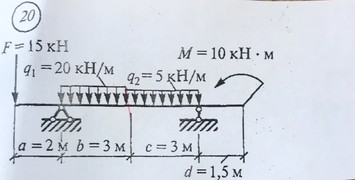
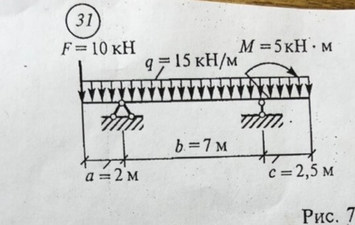
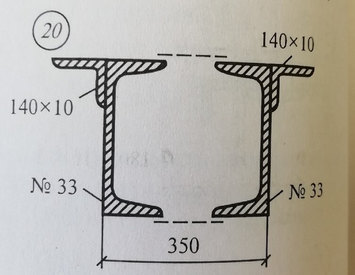
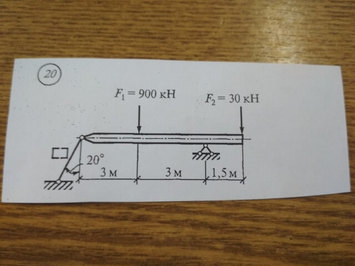
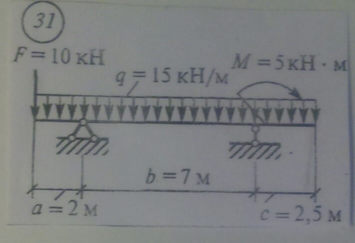
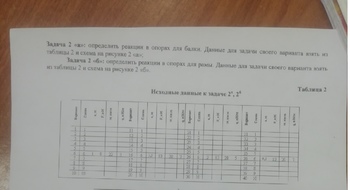
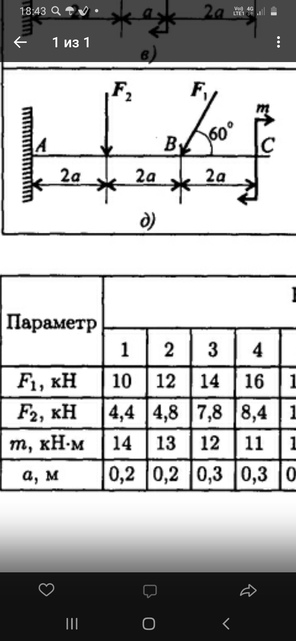
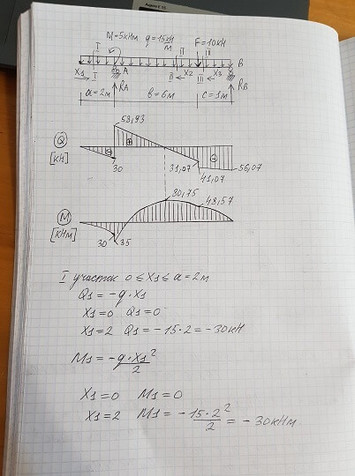
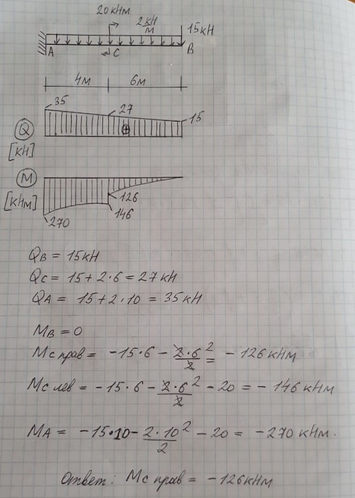
Задача № 20 Определить опорные реакции балки.Проверить правильность их определения
Ответ к задачи № 20 Определить опорные реакции балки.Проверить правильность их определения
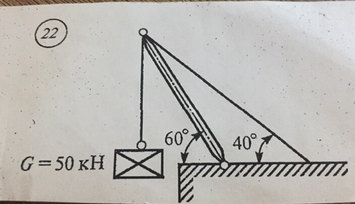
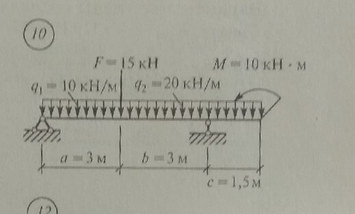
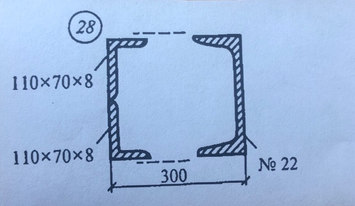
Задача № 22 Задача № 22 найти R(a) и R(b)
Ответ к задачи Задача № 22 найти R(a) и R(b)
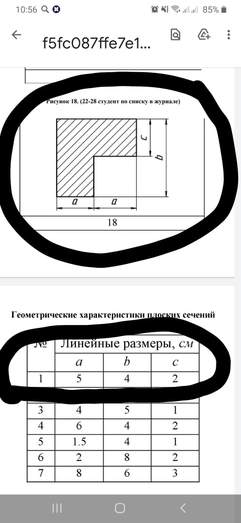
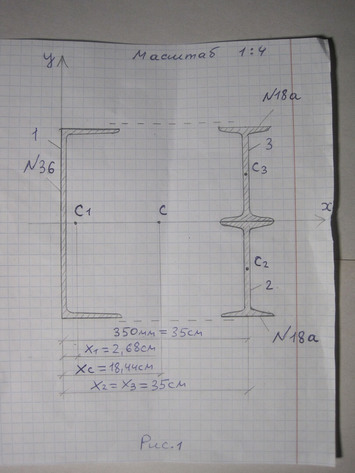
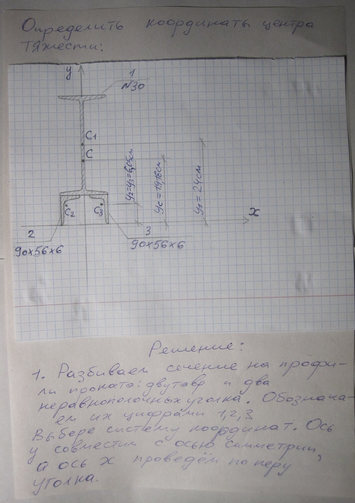
Задача Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже
Ответ к задачи Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже
Задача № 10 Найти реакцию опор
Ответ к задачи №10 Найти реакцию опор
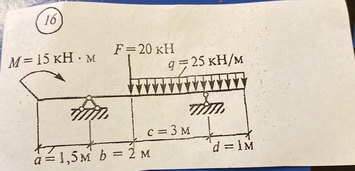
Задача № 16 Определить опорные реакции балки.Проверить правильность их определения
Ответ к задачи № 16
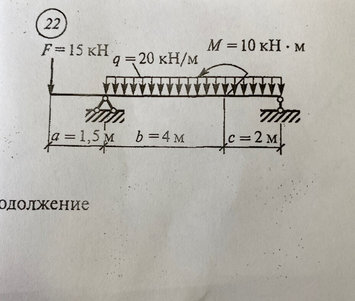
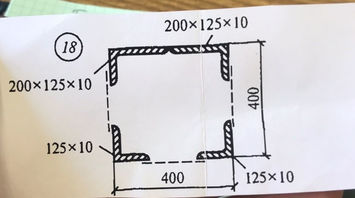
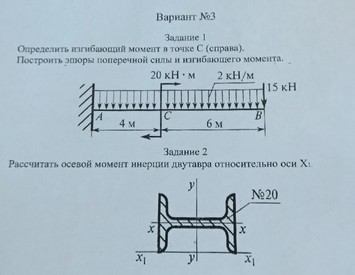
Задача № 22 Определить опорные реакции балки. Проверить правильность их определения
Ответ к задачи № 22 Определить опорные реакции балки Проверить правильность их определения
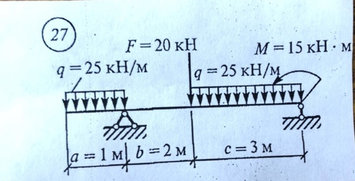
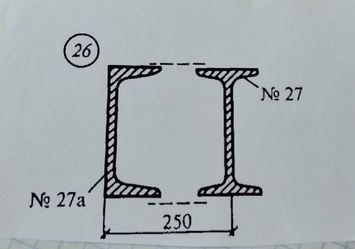
Задача № 27 Определить опорные реакции балки Проверить правильность их определения
Ответ к задачи № 27 Определить опорные реакции балки Проверить правильность их определения
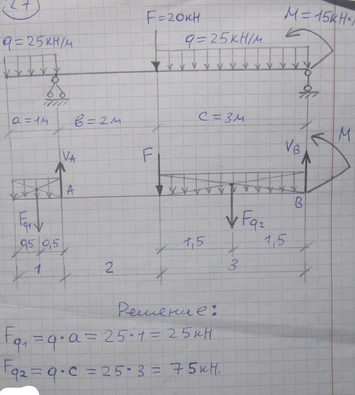
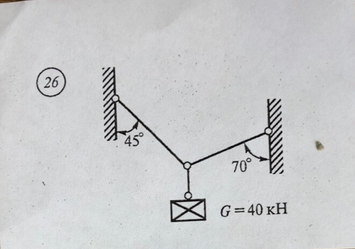
Задача № 26 Определить опорные реакции балки Проверить правильность их определения
Ответ к задачи № 26 Определить опорные реакции балки Проверить правильность их определения
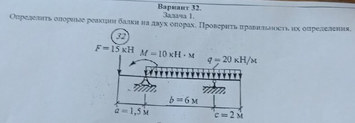
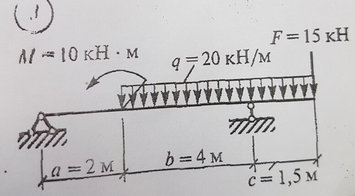
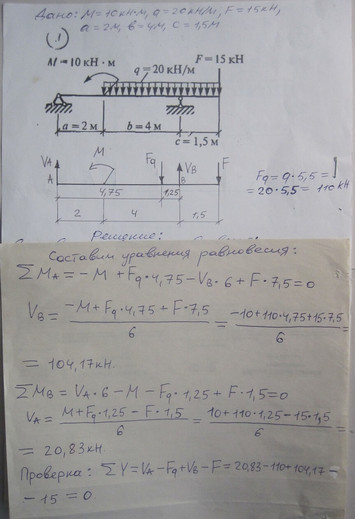
Вариант 32 задача № 1Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Ответ к варианту 32 задача №1Определить опорные реакции балки на двух опорах. Проверить правильность их определения
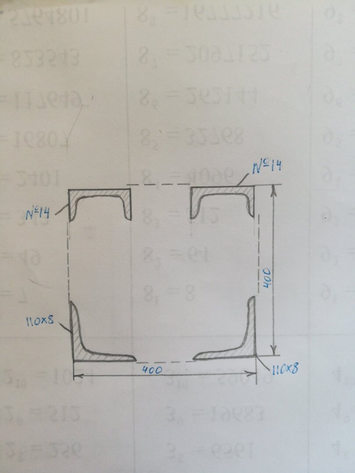
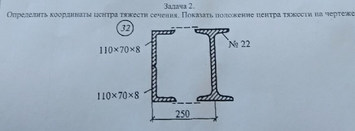
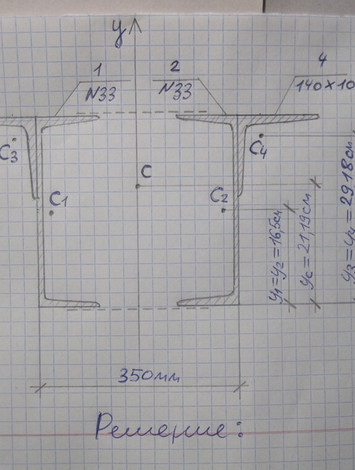
Вариант 32 задача №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
Ответ к варианту 32 №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
Решение к варианту 32 № 2
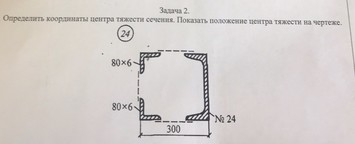
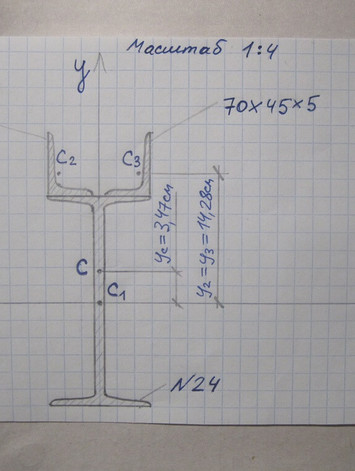
Вариант 24 задача № 2 Определить координаты центра тяжести сечения Показать положения центра тяжести на чертеже
Ответ к варианту 24 задача № 2 Определить координаты центра тяжести сечения
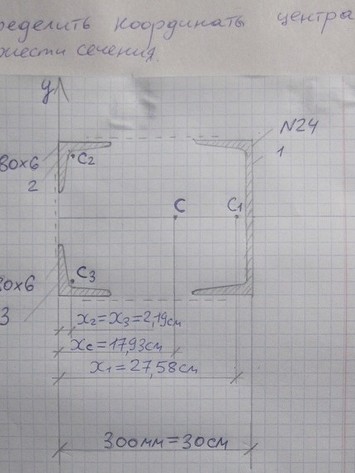
Задача Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба
Ответ к задачи Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба
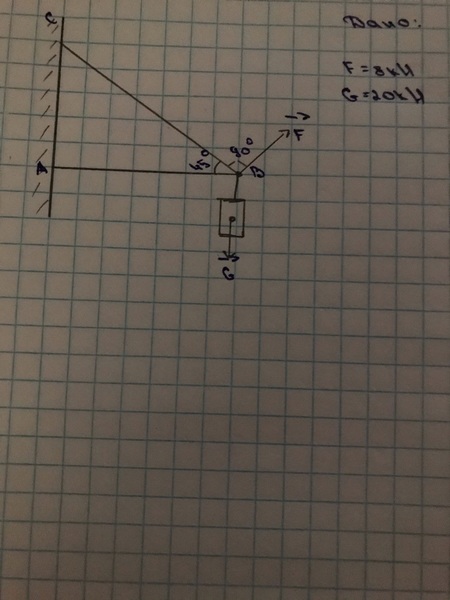
Задача — Определить величину и направления реакцию связей
Ответ к задаче -Определить величину и направления реакций связей
Задача- Определить опорные реакции балки на 2-х опорах
Ответ к задачи Определить опорные реакции балки на 2-х опорах
Задача № 9 Найти центр тяжести
Ответ к задаче № 9 найти центр тяжести
Найти центр тяжести
Решение к задаче Найти центр тяжести
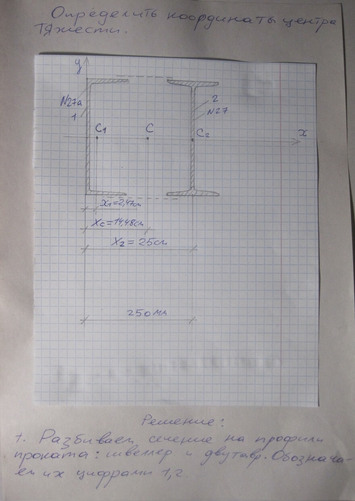
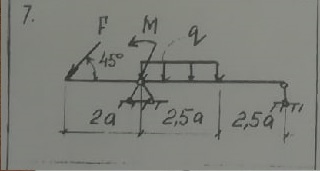
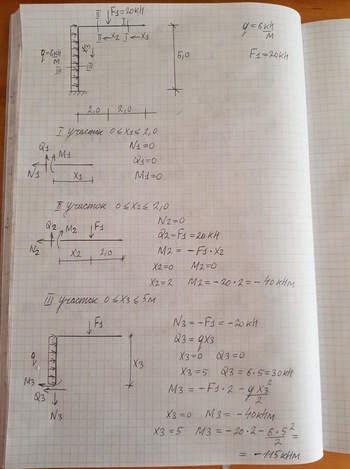
Решение к задаче № 7
28 задача Определить положение координаты центра тяжести
Ответ к 28 задачи Определить положение координаты центра тяжести
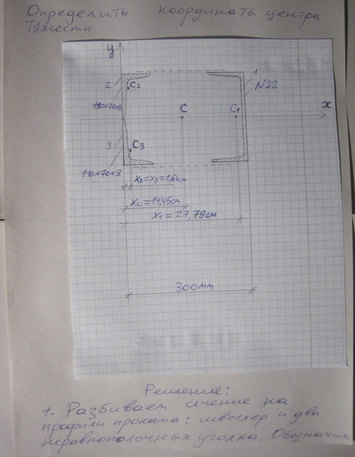
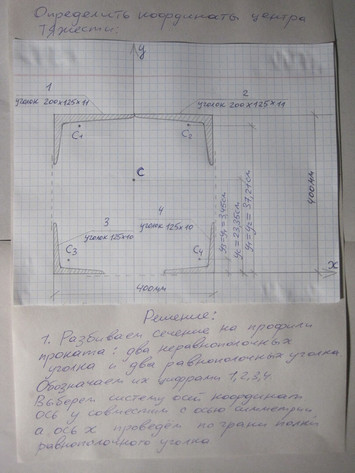
Ответ к задаче — Момент силы относительно точки
Задача — Понятие о внецентренном растяжении ( сжатии)
Ответ к задаче — Понятие о внецентренном растяжении ( сжатии)
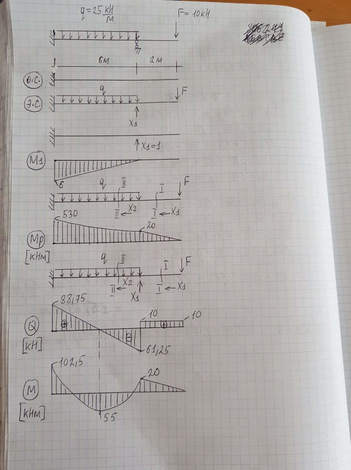
Ответ к заданию для Натальи Добринской
Рисунок Д вариант чисел 1 Задача
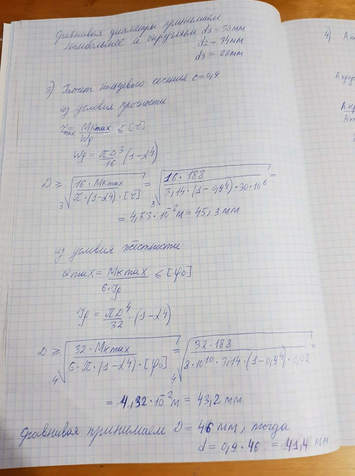
ПЕРЕХОДИ НА ДРУГУЮ СТРАНИЦУ САЙТА
ОТВЕТЫ ПО ТЕХ-МЕХУ НА СЛЕДУЮЩЕЙ СТРАНИЦЕ
Мы занимаемся установкой систем вентиляции и кондиционирования в Подольске с 2009 года, затем география наших услуг расширилась до городов Щербинка, Чехов, Серпухов, Домодедово.
Сейчас наши специалисты выезжают в города по всей Московской области. Квалификация подтверждается ежегодно, путём прохождения аттестации в климатических компаниях мировых лидеров.
Полученные знания и навыки позволяют нам найти и решить проблему любой сложности.
Наши цены Вас приятно удивят!
Монтаж кондиционера или вентиляционного оборудования можно заказать по телефонам в Подольске, Чехове, Щербинке и других городах Московской области
О Компании
Климатическая техника сегодня – уже не роскошь, а иногда, это даже потребность и необходимость. Чтобы Ваш дом был полон заботы и комфорта, кондиционер – одна из его немногих составляющих.
Меню опросов
Контакты
Адрес: МО, Г.о. Подольск,
Железнодорожная 2б, офис1
📽️ Видео
Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать
Уравнение прямой на плоскостиСкачать
2. Уравнение плоскости примеры решения задач #1Скачать
Уравнения прямой на плоскости | Векторная алгебраСкачать
Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать
3. Частные случаи общего уравнения плоскости Неполные уравнения плоскостиСкачать
§8.1 Общее уравнение прямой на плоскостиСкачать
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать
11 класс, 8 урок, Уравнение плоскостиСкачать
Видеоурок "Уравнение плоскости в отрезках"Скачать
Уравнение плоскости. 11 класс.Скачать
5. Нормальное уравнение плоскости выводСкачать
Анализ общего уравнения плоскостиСкачать
§36 Векторные уравнения прямой на плоскостиСкачать
Лекция 25. Виды уравнений плоскости в пространстве.Скачать
