Уравнение описывающее гармонические колебания тела определяется формулой х a sin t 0

Видео:10 класс, 19 урок, График гармонического колебанияСкачать

Тестирование онлайн

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

Видео:Урок 327. Гармонические колебанияСкачать

График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Видео:Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Видео:Гармонические колебания | Физика 11 класс #8 | ИнфоурокСкачать

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Видео:Выполнялка 53.Гармонические колебания.Скачать

Как получить зависимости v(t) и a(t)

Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).

При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.

Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Гармонические колебания

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Видео:Превращение энергии при колебаниях. Уравнение колебательного движения. 1 часть. 9 класс.Скачать

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Видео:Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Видео:Урок 343. Затухающие колебания (часть 1)Скачать

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Видео:5.4 Уравнение гармонических колебанийСкачать

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний

T = t/N

N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .

Она используется в уравнении гармонических колебаний:

Видео:Физика ЦТ | Механические колебания. Часть1. Уравнение колебаний гармонического осциллятораСкачать

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

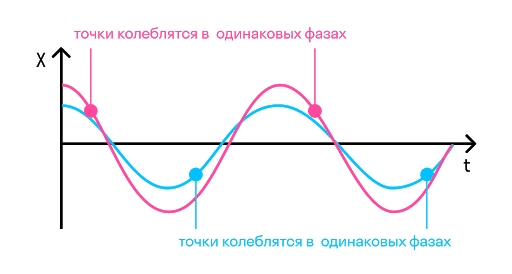
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

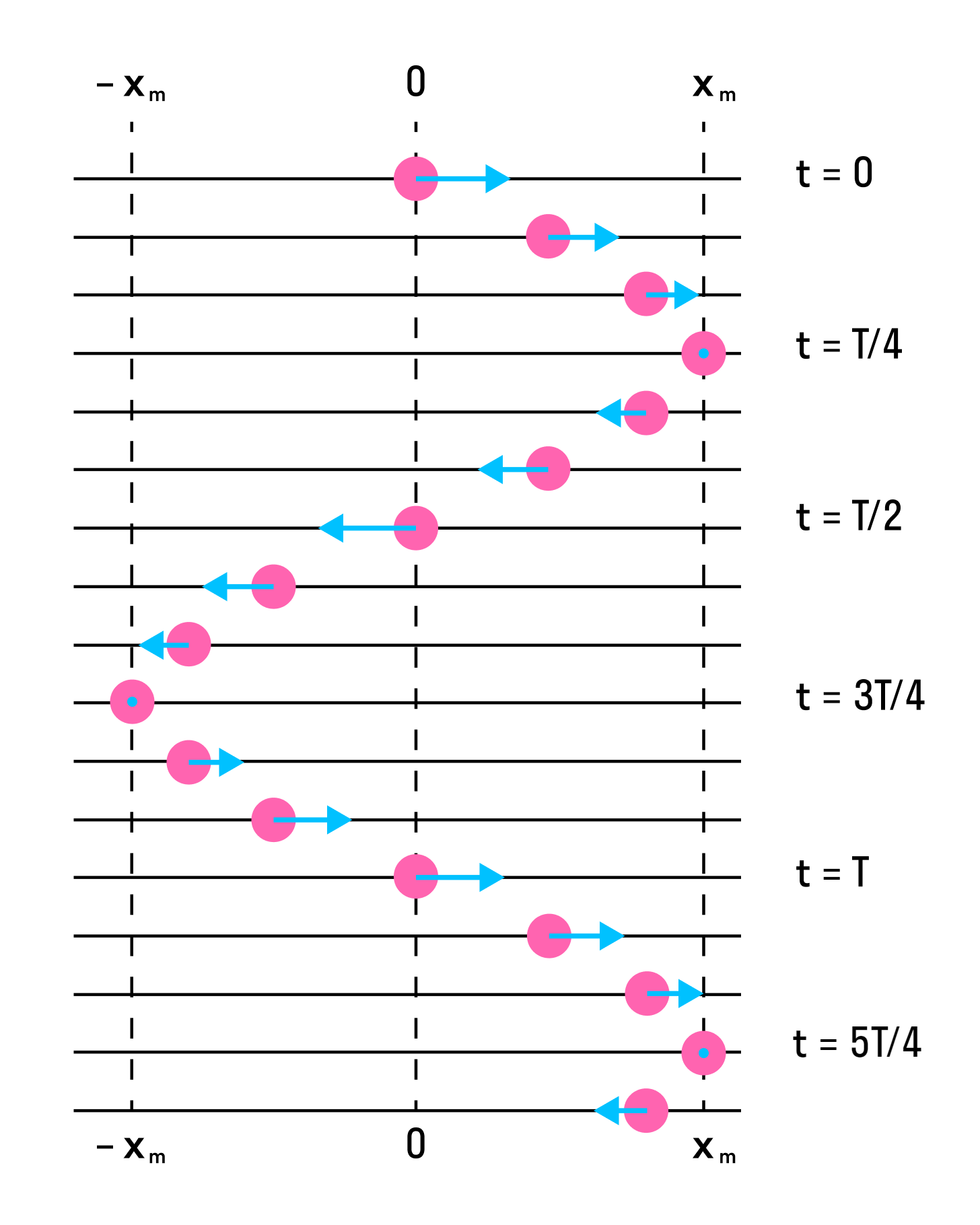
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Видео:Урок 329. Задачи на гармонические колебания - 1Скачать

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Видео:Урок 335. Анализ графика гармонических колебанийСкачать

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Видео:10й класс; Физика; "Решение задач. Гармонические колебания"Скачать

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Видео:Урок 325. Колебательное движение и его характеристикиСкачать

Гармоническое колебание (пример формулы)

Гармоническое колебание это простейшее периодическое колебание, при котором смещение х меняется со временем по закону синуса (или косинуса).

Видео:9 класс. Уравнение гармонических колебаний. Для сдающих ОГЭ.Скачать

Видео:Физика 10 класс. Гармонические колебания. Решение задачСкачать

Что такое гармоническое колебание

Это периодически повторяющееся движение, при котором тело отклоняется от некоторого среднего положения то в одну, то в другую сторону, называется колебательным движением; этот вид движения весьма распространен в природе.

Оно свойственно частицам вещества: атомам и молекулам, с колебательным движением частиц среды связаны звуковые явления, оно лежит в основе многих электриче ских явлении, например переменного тока, электрических колебаний, электромагнитных волн и т. п.

Изучение колебательного движения начнем с наиболее простого случая — механических колебаний. При этом обратим главное внимание на колебательное движение таких тел, которые имеют только одно положение устойчивого равновесия.

Если такое тело выведено из положения равновесия внешней силой, то оно под действием внутренних сил возвращается в него постепенно путем многократных колебаний около этого положения.

Такое колебательное движение могут совершать, например ножки камертона, натянутая струна, любое свободно подвешенное тело (качели, маятник) и т. п.

При колебательном движении положение тела в каждый данный момент времени определяется расстоянием его от среднего положения, которое называется смещением, а также направлением движения.

Весьма распространенным видом колебательного движения является простое, или гармоническое, колебание.

Оно происходит под действием силы, прямо пропорциональной смещению и направленной к положению равновесия.

Характерным признаком гармонического колебания является изменение смещения во времени по закону синуса или косинуса.

Пример гармонического колебания

В качестве примера рассмотрим свободное колебание горизонтального пружинного маятника (рис. 2, а).

Маятник состоит из тела С, подвешенного к стойке АВ, с помощью тяги АС и упорного стержня ВС, которые могут свободно поворачиваться вокруг оси стойки.

Такая подвеска полностью уравновешивает силу тяжести тела С при любом его положении.

С обеих сторон к телу С прикреплены пружины F, закрепленные в неподвижной раме Е. При отклонении тела С от среднего положения одна из пружин растягивается. Сила F, с которой пружина действует на тело, прямо пропорциональна его смещению s и направлена в сторону, обратную смещению:

где k — коэффициент пропорциональности, зависящий от свойств пружины, а знак минус указывает, что действие силы обратно направлению смещения.

Если отклонить тело С из среднего положения и затем представить действию упругих сил пружин, то оно будет совершать колебательное движение: возвратившись под действием силы пружин к среднему положе нию, тело по инерции пройдет его и отклонится в противоположную сторо ну; достигнув максимального отклонени я , тело под действием силы пружин снова возвратится в исходное сложение, по инерции пройдет его в обратном направлении и т. д.

Как характеризуются колебательные движения

Колебательное движение, в том числе и гармоническое колебание, характеризуются:

1. Наибольшим смещением или амплитудой колебания
2. Периодом колебания или временем, в течение которого совершается одно полное колебание.

Период колебания Т измеряется в секундах. Вместо периода колебание можно характеризовать частотой v. Частота колебаний— это величина, обратная периоду v = 1/Т.

Иначе, частота — это число колебаний, которое тело совершает в течение 1 сек. Размерность частоты 1/сек или сек -1 . Практически частота измеряется в единицах, называемых герц (гц).

Герц — это частота, при которой за 1 сек происходит одно полное колебание. В герцах измеряют частоту колебаний любой природы.

Изучение колебаний

Гармоническое колебание удобно изучать, например, с помощью модели. На горизонтальном диске А, который вращается с постоянной скоростью, укреплен на стержне маленький шарик N.

Шарик совершает равномерное движение по окружности. Рассмотрим движение, которое совершает точка п, являющаяся проекцией шарика N на любой из диаметров окружности.

В качестве проекции шарика на диаметр окружности можно рассматривать его тень, отбрасываемую на экран Э, установленный рядом с диском перпендикулярно направлению световых лучей. При вращении диска тень шарика на экране будет совершать колебательное движение.

Составим уравнение для этого движения, которое связывает между собой смещение s, амплитуду а и период Т (или частоту v) колебания и таким образом позволяет определить величину и знак смещения в любой заданный момент времени.

Рассмотрим положение точек N и п в какой-либо момент времени t (рис. 3). Соединим точку N с центром окружности. Радиус ON совершает вращательное движение с угловой скоростью:

ω = 2 π /Т ,

где Т — есть период обращения. За начало отсчета времени t = 0 примем момент, когда точка N находится на горизонтальном диаметре, а точка п соответственно — в центре окружности. Тогда угол φ, пройденный радиусом ON за время t , будет:

Из треугольника ONn (угол при вершине которого равен углу φ как угол имеющий параллельные стороны) следует, что On = ON sin φ, где On — смещение s точки п в момент времени t, ON —радиус окружности или амплитуда а колебания. Подставляя эти значения, получим:

s = a sin φ = a sin ωt.

Смещение изменяется от времени по закону синуса, следовательно, точка п совершает гармоническое колебание. Уравнению можно придать также и несколько иной вид:

s = a sin( 2 π t/Т) = a sin 2 π vt

Величина, находящаяся под знаком синуса, т. е.

φ = ωt = 2 π vt = 2 π t/Т

называется фазой колебания и измеряется в градусах или радианах. Величину ω = 2 π v = 2 π t/Т входящую в выражение для фазы колебания, называют к руговой частотой гармонического колебания.

Что такое ф аза колебания

Фаза колебания есть величина, характеризующая состояние колебательного процесса в каждый заданный момент времени.

Зная фазу колебания и его амплитуду, можно для любого момента времени определить величину и знак смещения, т. е. определить положение колеблющегося тела.

Имея в виду, что определенным частям периода соответствуют определенные величины фазы колебания, можно, зная эти величины и найдя соответствующие им синусы углов, определить величину смещения в долях амплитуды а.

Можно построить график, соответствующий уравнению гармонического колебания. График показывает изменение смещения s тела (откладывается по оси ординат) от времени t, которое отложено по оси абсцисс.

По форме график является синусоидой (рис. 4) и может быть построен, пользуясь данными таблицы.

График колебания

График колебания можно получить также и путем непосредственной записи движения тела на равномерно движущейся бумажной ленте.

Например, к телу С нашего горизонтального маятника можно прикрепить воронку с мелким песком, а под ним расположить лист смазанной клеем белой бумаги, который равномерно передвигается в направлении, перпендикулярном направлению колебаний (см. рис. 2, а).

Тогда песочная струйка запишет на бумаге кривую (см. рис. 2, б), ординаты которой соответствуют смещениям маятника в различные последующие моменты времени.

Полученная таким образом кривая совпадает по характеру с графиком (рис. 4). В обоих случаях кривые изображают колебание, развернутое по времени: каждая точка кривой является концом ординаты, изображающей смещение тела в последующие, равномерно расположенные по горизонтальной оси моменты времени.

В первом случае это получается в результате движения ленты, во втором — это обеспечивается в самом процессе построения графика.

Амплитуда гармонических колебаний

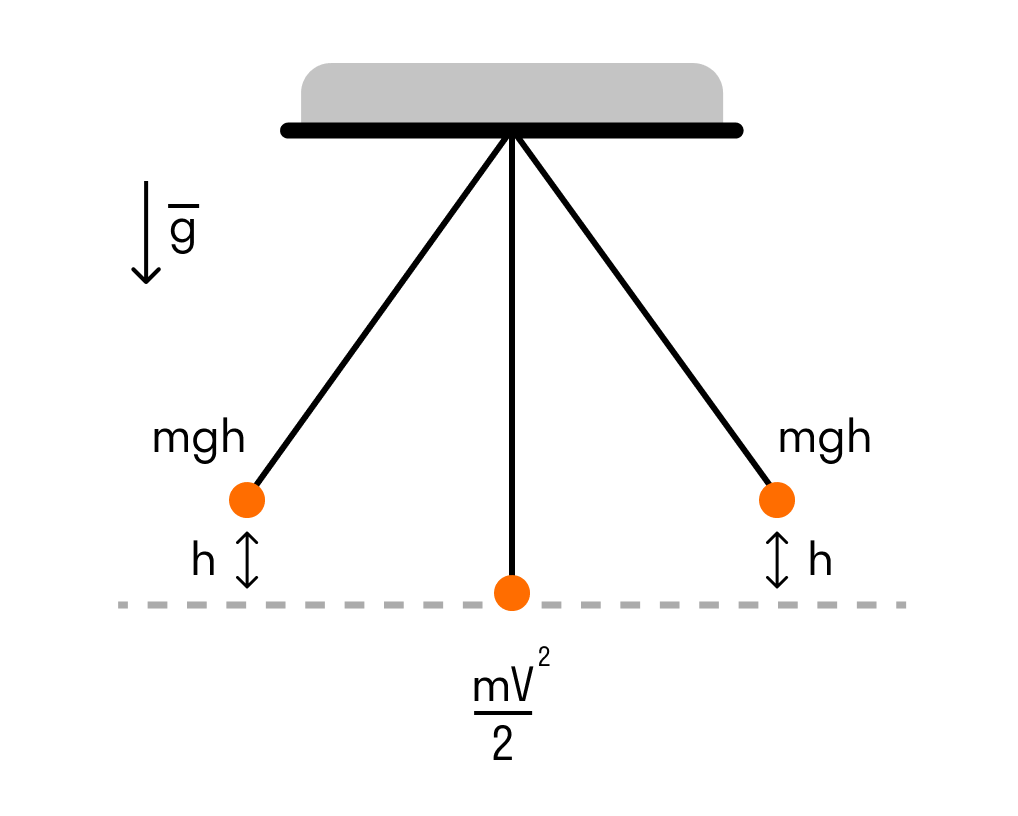
Энергия Е тела, совершающего гармоническое колебание, состоит из кинетической и потенциальной, которые в процессе колебания периодически переходят одна в другую.

В момент наибольшего смещения скорость тела на мгновение делается равной нулю и вся энергия тела является потенциальной:

По мере движения тела к положению равновесия скорость его увеличивается и потенциальная энергия постепенно переходит в кинетическую.

При прохождении телом положения равновесия скорость его максимальна и вся энергия переходит в кинетическую:

Определим эту энергию. рассмотренной модели гармонического колебания (см. рис. 2) наибольшая скорость υ_m точки п при прохождении среднего положения равняется скорости υ движения точки N по окружности, так как в этот момент скорости этих точек параллельны и одинаковы по величине.

Эта скорость υ_m = 2 π а/Т, где а — амплитуда колебания или радиус окружности, а Т — период колебания. Поэтому для энергии Е тела с массой т, совершающего гармоническое колебание, можно написать следующее выражение:

Подставляя значение скорости υ_m, получаем:

Е = (mυ 2 m)/2 = m/2((2 π a/T) 2 ) = 2 π 2 ma 2 v 2

Энергия тела, совершающего гармоническое колебание, прямо пропорциональна массе тела, квадрату амплитуды и квадрату частоты.

Пример амплитуды гармонических колебаний

Рассмотрим колебание тела, которое началось на промежуток времени t₀ раньше момента начала отсчета времени (обычно время t₀ выражают в долях периода Т колебания).

В этом случае к началу отсчета времени тело уже имеет смещение s₀, как это показано на графике рис. 5 , а. Смещению s₀ соответствует фаза колебания φ₀, которая называется начальной фазой, и по общему правилу может быть представлена так:

Составим уравнение для данного колебания . Угол φ ‘, определяющий положение радиуса точки N в момент времени t, будет φ ‘= φ + φ₀ . где φ₀ —угол, соответствующий начальной фазе колебания (величина постоянная), а φ — угол, образуемый при движении точки N и прямо пропорциональный промежутку времени t: φ =ωt.

Тогда, рассуждая аналогично предыдущему случаю (см. рис 3), можно написать:

График колебания, описываемый этим уравнением, изображен на рис. 5 , а.

Рассуждая аналогично, можно убедиться, что если колебание началось на промежуток времени t₀ позже начала отсчета времени, то его уравнение будет иметь вид:

Его график изображен на рис. 5 , б.

Если два колебания одинаковой частоты начинаются одновременно, то говорят, что они имеют одинаковую фазу или что они находятся в фазе.

Если сопоставляются два колебания одинаковой частоты, начавшиеся не одновременно, то говорят, что они имеют разность фаз или сдвиг фазы φ_{1- 2}, соответствующий разнице во времени t_1-2 между началами колебания (рис. 5, в).

При этом одно из них называют опережающим (или наоборот, запаздывающим) по фазе относительно другого.

Про два колебания, разность фаз у которых составляет π или 180°, говорят, что они находятся в противофазе.

Связь между гармоническим колебанием и равномерным движением по окружности

Представим себе произвольную точку D, равномерно вращающуюся по окружности радиуса А против часовой стрелки с постоянной угловой скоростью ω рад/с (рис. ). Уравнение движения точки D примет вид

где φ — угол поворота подвижного радиуса 0D относительно неподвижного OK, а φ₀ — начальное значение угла φ в момент времени t = 0.

В то время как точка D вращается по окружности от К к L и снова к K, проекция точки D на диаметр MN — точка D’ — движется вдоль отрезка МN от одного из его концов к другому и обратно, совершая колебательное движение.

Обозначим расстояние 0D’ через х. Тогда уравнение движения точки D’можно записать в виде

Если в момент времени t = 0 начальное значение угла φ₀ = 0, то уравнение движения точки D’ примет вид

х = A sin φ = A sin ωt.

Функция sin ωt является простейшей периодической функцией от времени, значит точка D’ совершает периодические колебания.

Если на оси ординат откладывать значения смещения х, а на оси абсцисс время t, то можно получить график гармонического колебания, который представляет собой синусоиду.

Поскольку sin φ меняется в пределах от +1 до —1, то смещение х точки D’ от центра колебаний 0 находится в пределах:

—A≤x≤A.

Максимальная величина этого смещения |х |макс = A называется амплитудой колебания.

Затухающие и незатухающие колебания

Колебания, происходящие с неизменной амплитудой, называются незатухающими. Колебания, происходящие с уменьшающейся амплитудой, называются затухающими.

Чтобы поддерживать незатухающие колебания, необходимо создать такой механизм, который за одно полное колебание точки сообщит ей дополнительно столько энергии, сколько потеряно точкой за это же время на преодоление трения, сопротивления и т. п.

Аргумент ωt стоящий под знаком синуса, называется фазой колебания. Величина со, характеризующая угловую скорость вращения точки D, называется циклической частотой гармонического колебания точки D’.

Время, в течение которого тело совершает одно полное колебание (время между двумя последовательными прохождениями точки через положение равновесия в одном и том же направлении), называется периодом полного колебания Т.

Время движения колеблющегося тела от положения равновесия до максимального отклонения и обратно до положения равновесия называется периодом простого колебания. Период простого колебания равен половине периода полного колебания.

Циклическая частота со связана с периодом Т и обычной частотой v (v — число колебаний за единицу времени) такими соотношениями

ω = 2 π/Т

ω = 2 π v .

Частота v измеряется в герцах. 1 Гц равен 1 колебанию в секунду. Фазу колебания φ можно записать в виде

Фаза показывает, какая часть периода прошла от момента начала колебания.

Статья на тему Гармоническое колебание

Похожие страницы:

Понравилась статья поделись ей

Leave a Comment

Для отправки комментария вам необходимо авторизоваться.