Уравнение окружности в сферических координатах (6 видео)

Формулы аналитической геометрии в пространстве

$d=sqrt$

НАПРАВЛЯЮЩИЙ КОСИНУС ЛИНИИ, СОЕДИНЯЮЩЕЯ ТОЧКИ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$
$l=cosalpha=frac$, $m=cosbeta=frac$, $n=cosgamma=frac$

где $alpha,beta,gamma$ углы, которые линия $P_1P_2$ образовывает с положительными осями $x,y,z$ соответственно, а $d$ определено на рисунке вверху.

ОТНОШЕНИЕ МЕЖДУ НАПРЯВЛЯЮЩИМИ КОСИНУСАМИ
$cos^2alpha+cos^2beta+cos^2gamma=1$ или $l^2+m^2+n^2=1$

НАПРАВЛЯЮЩИЕ ЧИСЛА
Числа $L,M,N$, которые есть пропорциональны к направляющим косинусам $l, m, n$ называются направляющими числами. Отношение между ними

Это также действительно, если $l, m, n$ заменяются на $L, M, N$ соответственно.

УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ
$x=x_1+lt$, $y=y_1+mt$, $z=z_1+nt$

Это также действительно если $l, m, n$ заменяются на $L, M, N$ соответственно.

УГОЛ $phi$ МЕЖДУ ДВУМЯ ЛИНЯМИ С НАПРАВЛЯЮЩИМИ КОСИНУСАМИ $l_1, m_1, n_1$ И $l_2, m_2, n_2$
$cosphi=l_1l_2+m_1m_2+n_1n_2$

ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
$Ax + By + Cz + D = 0$ [$A, B, C, D$ — константы]

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКИ $(x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)$

$beginx-x_1 & y-y_1 & z-z_1\ x_2-x_1 & y_2-y_1 & z_2-z_1\ x_3-x_1 & y_3-y_1 & z_3-z_1end=0$

$begin y_2-y_1 & z_2-z_1\ y_3-y_1 & z_3-z_1end(x-x_1)$ $+begin z_2-z_1 & x_2-x_1\ z_3-z_1 & x_3-x_1end(y-y_1)$ $+begin x_2-x_1 & y_2-y_1\ x_3-x_1 & y_3-y_1end(z-z_1)=0$

где $a, b, c$ есть пересечения на осях $x, y, z$ соответственно.

Обратите внимание, что направляющие числа для линии, перпендикулярной к плоскости $Ax + By + Cz + D = 0$ есть $A, B, C$.

где знак выбирается так, что расстояние не является отрицательным.

НОРМАЛЬНОЕ УРАВНЕНИЯ ПЛОСКОСТИ
$xcosalpha+ycosbeta+zcosgamma=p$

где $p$ = перпендикулярному расстоянию от $O$ к плоскости в $P$ и $alpha, beta, gamma$ есть углами между $OP$ и положительными осями $x, y, z$.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ
$left<beginx=x’+x_0\ y=y’+y_0\ z=z’+z_0endright.$ $left<beginx’=x-x_0\ y’=y-y_0\ z’=z-z_0endright.$

где $(x, y, z)$ — старые координаты [т.e. координаты относительно системы xyz], $(x’, y’, z’)$ — новые координаты [относительно системы $x’y’z’$] и $(x_0,y_0,z_0)$ координаты нового центра $O’$ относительно старой координатной системы $xyz$.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ВРАЩЕНИИ

где центры систем $xyz$ и $x’y’z’$ находятся в одной точке и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ И ВРАЩЕНИИ

$left<beginx=l_1x’+l_2y’+l_3z’+x_0\ y=m_1x’+m_2y’+m_3z’+y_0\ z=n_1x’+n_2y’+n_3z’+z_0endright.$

$left<beginx’=l_1(x-x_0)+m_1(y-y_0)+n_1(z-z_0)\ y’=l_2(x-x_0)+m_2(y-y_0)+n_2(z-z_0)\ z’=l_3(x-x_0)+m_3(y-y_0)+n_3(z-z_0)endright.$

где $O’$ системы $x’y’z’$ имеет координаты $(x_0,y_0,z_0)$ относительно системы $xyz$ и $l_1,m_1,n_1; l_2,m_2,n_2; l_3,m_3,n_3$ направляющие косинусы осей $x’, y’, z’$ относительно осей $x, y, z$ соответственно.

ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ $(r, theta, z)$
Точка $P$ может быть определена как цилиндрическими координатами $(r, theta, z)$, так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя координатами есть

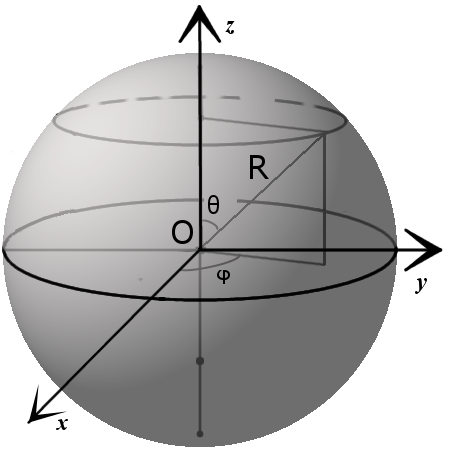
СФЕРИЧЕСКИЕ КООРДИНАТЫ $(r, theta, phi)$
Точка $P$ может быть определена как сферическими координатами $(r, theta, phi)$ так и прямоугольными координатами $(x, y, z)$.
Преобразование между этими двумя кординатами есть

$left<beginx=rsinthetacosphi\ y=rsinthetasinphi\ z=rcosthetaendright.$

УРАВНЕНИЕ СФЕРЫ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
$(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$

где сфера имеет центр $(x_0,y_0,z_0)$ и радиус $R$.

УРАВНЕНИЕ СФЕРЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
$r^2-2r_0r(theta-theta_0)+r_0^2+(z-z_0)^2=R^2$

где сфера имеет центр $(r_0;theta_0;z_0)$ в цилиндрических координатах и радиус $R$.

Если центр находится в начале координат, уравнение имеет вид:

УРАВНЕНИЕ СФЕРЫ В СФЕРИЧЕСКИХ КООРДИНАТАХ
$r^2+r_0^2-2r_0 rsinthetasintheta_0cos(phi-phi_0)=R^2$

где сфера имеет центр $(r_0; theta_0; phi_0)$ в сферических координатах и радиус $R$.

Если центр в начале координат, уравнение имеет вид:

ЭЛЛИПТИЧЕСКИЙ ЦИЛИНДР С ОСЬЮ КАК $z$ ОСЬ
$frac+frac=1$

где $a, b$ — полуоси эллиптического сечения.
Если $b = a$, фигура превращается в цилиндрический цилиндр с радиусом $a$.

Обратите внимание на ориентацию осей этой фигуры.

Содержание

Уравнение окружности в сферических координатах
Основные положения сферической геометрии
Прямые, отрезки, расстояния и углы на сфере
Сферический треугольник
Координаты на сфере
Уравнение окружности в сферических координатах
Формулы аналитической геометрии в пространстве
Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Уравнение сферы
Основные свойства сферы и шара
Секущая, хорда, секущая плоскость сферы и их свойства
Касательная, касательная плоскость к сфере и их свойства
Уравнение окружности в сферических координатах
🎦 Видео

Видео:Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать

Уравнение окружности в сферических координатах

Сферическая геометрия – математическая дисциплина, изучающая геометрические образы (точки, линии, фигуры), находящиеся на сфере, и соотношения между ними.

По-видимому, первым обращением человечества к тому, что потом получит название сферической геометрии, была планетарная теория греческого математика Евдокса (ок. 408–355), одного из участников Академии Платона. Это была попытка объяснить движение планет вокруг Земли с помощью четырех вращающихся концентрических сфер, каждая из которых имела особую ось вращения с концами, закрепленными на охватывающей сфере, к которой, в свою очередь, были «прибиты» звезды. Таким образом объяснялись замысловатые траектории планет (в переводе с греческого «планета» – блуждающая). Именно благодаря такой модели древнегреческие ученые умели достаточно точно описывать и предсказывать движения планет. Это было необходимо, например, в мореплавании, а так же во многих других «земных» задачах, где нужно было учитывать, что Земля – не плоский блин, покоящийся на трех китах. Значительный вклад в сферическую геометрию внес Менелай из Александрии (ок. 100 н.э.). Его труд Сферика стал вершиной достижений греков в этой области. В Сферике рассматриваются сферические треугольники – предмет, которого нет у Евклида. Менелай перенес на сферу евклидову теорию плоских треугольников и в числе прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая, причем, в отличие от Птолемея (ок. 150), у которого в работах немало вычислений, трактат Менелая геометричен строго в духе евклидовой традиции.

Основные положения сферической геометрии

Всякая плоскость, пересекающая сферу, дает в сечении окружность. Если плоскость проходит через центр сферы, то в сечении получается так называемый большой круг. Через любые две точки на сфере, кроме диаметрально противоположных, можно провести единственный большой круг. (На глобусе примером большого круга служит экватор и все меридианы.) Через диаметрально противоположные точки проходит же бесконечное количество больших кругов. Меньшая дуга AmB (рис. 1) большого круга является кратчайшей из всех линий на сфере, соединяющих заданные точки. Такая линия называется геодезической. Геодезические линии играют на сфере ту же роль, что и прямые в планиметрии. Многие положения геометрии на плоскости справедливы и на сфере, но, в отличие от плоскости, две сферические прямые пересекаются в двух диаметрально противоположных точках. Таким образом, в сферической геометрии просто не существует понятия параллельности. Еще одно отличие – сферическая прямая замкнута, т.е. двигаясь по ней в одном и том же направлении, мы вернемся в исходную точку, точка не разбивает прямую на две части. И еще один удивительный с точки зрения планиметрии факт – треугольник на сфере может иметь все три прямых угла.

Рисунок 1 – Сферическая прямая

Прямые, отрезки, расстояния и углы на сфере

Прямыми на сфере считаются большие окружности. Если две точки принадлежат большой окружности, то длина меньшей из дуг, соединяющих эти точки, определяется как сферическое расстояние между этими точками, а сама дуга – как сферический отрезок. Диаметрально противоположные точки соединены бесконечным числом сферических отрезков – больших полуокружностей. Длина сферического отрезка определяется через радианную меру центрального угла α и радиус сферы R (рис. 2), по формуле длины дуги она равна R α. Любая точка С сферического отрезка АВ разбивает его на два, и сумма их сферических длин, как и в планиметрии, равна длине всего отрезка, т.е. АОС + СОВ = АОВ. Для любой же точки D вне отрезка АВ имеет место сферическое неравенство треугольника : сумма сферических расстояний от D до А и от D до В больше АВ, т.е. AOD + DOB > AOB, – полное соответствие между сферической и плоской геометриями. Неравенство треугольника – одно из основополагающих в сферической геометрии, из него следует, что, как и в планиметрии, сферический отрезок короче любой сферической ломаной, а значит, и любой кривой на сфере, соединяющей его концы.

Рисунок 2 – Длина сферического отрезка

Таким же образом на сферу можно перенести и многие другие понятия планиметрии, в частности те, которые можно выразить через расстояния. Например, сферическая окружность – множество точек сферы, равноудаленных от заданной точки Р. Легко показать, что окружность лежит в плоскости, перпендикулярной диаметру сферы РР` (рис. 3), т.е. это обычная плоская окружность с центром на диаметре РР`. Но сферических центров у нее два: Р и Р`. Эти центры принято называть полюсами. Если обратиться к глобусу, то можно видеть, что идет речь именно о таких окружностях, как параллели, и сферическими центрами всех параллелей являются Северный и Южный полюса. Если диаметр r сферической окружности равен π/2, то сферическая окружность превращается в сферическую прямую. (На глобусе – экватор). В этом случае такую окружность называют полярой каждой из точек Р и P`.

Рисунок 3 – Сферическая окружность

Одним из важнейших понятий в геометрии является равенство фигур. Фигуры считаются равными, если одну на другую можно отобразить таким образом (поворотом и переносом), что сохранятся расстояния. Это верно и для сферической геометрии.

Углы на сфере определяются следующим образом. При пересечении двух сферических прямых a и b на сфере образуются четыре сферических двуугольника, подобно тому, как две пересекающиеся прямые на плоскости разбивают ее на четыре плоских угла (рис. 4). Каждому из двуугольников соответствует двугранный угол, образованный диаметральными плоскостями, содержащими a и b. А угол между сферическими прямыми равен меньшему из углов образуемых ими двуугольников.

Рисунок 4 – Углы на сфере

Отметим так же, что угол ABC, образованный на сфере двумя дугами большого круга, измеряют углом A`BC` между касательными к соответствующим дугам в точке В (рис. 5) или двугранным углом, образованным диаметральными плоскостями, содержащими сферические отрезки АВ и ВС.

Рисунок 5 – Угол на сфере, образованный дугами большого круга

Точно так же, как и в стереометрии, каждой точке сферы сопоставляется луч, проведенный из центра сферы в эту точку, а любой фигуре на сфере – объединение всех пересекающих ее лучей. Так, сферической прямой соответствует содержащая ее диаметральная плоскость, сферическому отрезку – плоский угол, двуугольнику – двугранный угол, сферической окружности – коническая поверхность, ось которой проходит через полюсы окружности.

Многогранный угол с вершиной в центре сферы пересекает сферу по сферическому многоугольнику (рис. 6). Это область на сфере, ограниченная ломаной из сферических отрезков. Звенья ломаной – стороны сферического многоугольника. Их длины равны величинам соответствующих плоских углов многогранного угла, а величина угла при любой вершине А равна величине двугранного угла при ребре ОА.

Рисунок 6 – Многогранный угол

Сферический треугольник

Среди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Три больших окружности, пересекаясь попарно в двух точках, образуют на сфере восемь сферических треугольников. Зная элементы (стороны и углы) одного из них, можно определить элементы все остальных, поэтому рассматривают соотношения между элементами одного из них, того, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла ОАВС, углы треугольника – двугранными углами того же трехгранного угла (рис. 7).

Рисунок 7 – Трехгранный угол

Многие свойства сферического треугольника (а они одновременно являются и свойствами трехгранных углов) почти полностью повторяют свойства обычного треугольника. Среди них – неравенство треугольника, которое на языке трехгранных углов гласит, что любой плоский угол трёхгранного угла меньше суммы двух других. Или, например, три признака равенства треугольников. Все планиметрические следствия упомянутых теорем вместе с их доказательствами остаются справедливыми на сфере. Так, множество точек, равноудаленных от концов отрезка, будет и на сфере перпендикулярной к нему прямой, проходящей через его середину, откуда следует, что серединные перпендикуляры к сторонам сферического треугольника AВС имеют общую точку, точнее, две диаметрально противоположные общие точки Р и Р`, являющиеся полюсами его единственной описанной окружности (рис. 8). В стереометрии это означает, что около любого трёхгранного угла можно описать конус. Легко перенести на сферу и теорему о том, что биссектрисы треугольника пересекаются в центре его вписанной окружности.

Рисунок 8 – Описанная окружность сферического треугольника

Теоремы о пересечении высот и медиан также остаются верными, но их обычные доказательства в планиметрии прямо или косвенно используют параллельность, которой, на сфере нет, и потому проще доказать их заново, на языке стереометрии. Рис. 9 иллюстрирует доказательство сферической теоремы о медианах: плоскости, содержащие медианы сферического треугольника АВС, пересекают плоский треугольник с теми же вершинами по его обычным медианам, следовательно, все они содержат радиус сферы, проходящий через точку пересечения плоских медиан. Конец радиуса и будет общей точкой трех «сферических» медиан.

Рисунок 9 – Доказательство сферической теоремы о медианах

Свойства сферических треугольников во многом отличаются от свойств треугольников на плоскости. Так, к известным трем случаям равенства прямолинейных треугольников добавляется еще и четвертый: два треугольника АВС и А`В`С` равны, если равны соответственно три угла РА = РА`, РВ = РВ`, РС = РС`. Таким образом, на сфере не существует подобных треугольников, более того, в сферической геометрии нет самого понятия подобия, т.к. не существует преобразований, изменяющих все расстояния в одинаковое (не равное 1) число раз. Эти особенности связаны с нарушением евклидовой аксиомы о параллельных прямых и также присущи геометрии Лобачевского. Треугольники, имеющие равные элементы и различную ориентацию, называются симметричными, таковы, например, треугольники АС`С и ВСС` (рис. 10).

Рисунок 10 – Симметричные треугольники

Сумма углов всякого сферического треугольника всегда больше 180°. Разность А + В + С – π = d (измеряемая в радианах) – величина положительная и называется сферическим избытком данного сферического треугольника. Площадь сферического треугольника: S = R 2 d где R – радиус сферы, а d – сферический избыток. Эта формула впервые была опубликована голландцем А.Жираром в 1629 и названа его именем.

Если рассматривать двуугольник с углом a, то при 226 = 2π/n (n – целое число) сферу можно разрезать ровно на n копий такого двуугольника, а площадь сферы равна 4πR 2 = 4π при R = 1, поэтому площадь двуугольника равна 4π/n = 2α. Эта формула верна и при α = 2πm/n и, следовательно, верна для всех a. Если продолжить стороны сферического треугольника АВС и выразить площадь сферы через площади образующихся при этом двуугольников с углами А, В, С и его собственную площадь, то можно прийти к вышеприведенной формуле Жирара.

Координаты на сфере

Каждая точка на сфере вполне определяется заданием двух чисел; эти числа (координаты) определяются следующим образом (рис. 11). Фиксируется некоторый большой круг QQ` (экватор), одна из двух точек пересечения диаметра сферы PP`, перпендикулярного к плоскости экватора, с поверхностью сферы, например Р (полюс), и один из больших полукругов PAP`, выходящих из полюса (первый меридиан). Большие полукруги, выходящие из P, называются меридианами, малые круги, параллельные экватору, такие, как LL`, – параллелями. В качестве одной из координат точки M на сфере принимается угол q = POM (высота точки), в качестве второй – угол j = AON между первым меридианом и меридианом, проходящим через точку M (долгота точки, отсчитываемая против часовой стрелки).

Рисунок 11 – Координаты точки на сфере

В географии (на глобусе) в качестве первого меридиана принято использовать Гринвичский меридиан, проходящий через главный зал Гринвичской обсерватории (Гринвич – городской округ Лондона), он разделяет Землю на Восточное и Западное полушария, соответственно и долгота бывает восточной либо западной и измеряется от 0 до 180° в обе стороны от Гринвича. А вместо высоты точки в географии принято использовать широту, т.е. угол NOM = 90° – θ, отсчитываемый от экватора. Т.к. экватор делит Землю на Северное и Южное полушария, то и широта бывает северной либо южной и изменяется от 0 до 90°.

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Уравнение окружности в сферических координатах

Видео:§2 Различные уравнения окружностиСкачать

Формулы аналитической геометрии в пространстве

$d=sqrt $

НАПРАВЛЯЮЩИЙ КОСИНУС ЛИНИИ, СОЕДИНЯЮЩЕЯ ТОЧКИ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$
$l=cosalpha=frac $, $m=cosbeta=frac $, $n=cosgamma=frac $

ОТНОШЕНИЕ МЕЖДУ НАПРЯВЛЯЮЩИМИ КОСИНУСАМИ
$cos^2alpha+cos^2beta+cos^2gamma=1$ или $l^2+m^2+n^2=1$

Это также действительно, если $l, m, n$ заменяются на $L, M, N$ соответственно.

УРАВНЕНИЯ ЛИНИИ, СОЕДИНЯЮЩЕЙ $P_1(x_1,y_1,z_1)$ И $P_2(x_2,y_2,z_2)$ В ПАРАМЕТРИЧЕСКОЙ ФОРМЕ
$x=x_1+lt$, $y=y_1+mt$, $z=z_1+nt$

Это также действительно если $l, m, n$ заменяются на $L, M, N$ соответственно.

УГОЛ $phi$ МЕЖДУ ДВУМЯ ЛИНЯМИ С НАПРАВЛЯЮЩИМИ КОСИНУСАМИ $l_1, m_1, n_1$ И $l_2, m_2, n_2$
$cosphi=l_1l_2+m_1m_2+n_1n_2$

ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
$Ax + By + Cz + D = 0$ [$A, B, C, D$ — константы]

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКИ $(x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)$

$begin x-x_1 & y-y_1 & z-z_1\ x_2-x_1 & y_2-y_1 & z_2-z_1\ x_3-x_1 & y_3-y_1 & z_3-z_1end =0$

$begin y_2-y_1 & z_2-z_1\ y_3-y_1 & z_3-z_1end (x-x_1)$ $+begin z_2-z_1 & x_2-x_1\ z_3-z_1 & x_3-x_1end (y-y_1)$ $+begin x_2-x_1 & y_2-y_1\ x_3-x_1 & y_3-y_1end (z-z_1)=0$

где $a, b, c$ есть пересечения на осях $x, y, z$ соответственно.

Обратите внимание, что направляющие числа для линии, перпендикулярной к плоскости $Ax + By + Cz + D = 0$ есть $A, B, C$.

где знак выбирается так, что расстояние не является отрицательным.

НОРМАЛЬНОЕ УРАВНЕНИЯ ПЛОСКОСТИ
$xcosalpha+ycosbeta+zcosgamma=p$

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ВРАЩЕНИИ

ПРЕОБРАЗОВАНИЕ КООРДИНАТ ПРИ ПЕРЕМЕЩЕНИИ И ВРАЩЕНИИ

$left x=l_1x’+l_2y’+l_3z’+x_0\ y=m_1x’+m_2y’+m_3z’+y_0\ z=n_1x’+n_2y’+n_3z’+z_0endright.$

$left x’=l_1(x-x_0)+m_1(y-y_0)+n_1(z-z_0)\ y’=l_2(x-x_0)+m_2(y-y_0)+n_2(z-z_0)\ z’=l_3(x-x_0)+m_3(y-y_0)+n_3(z-z_0)endright.$

$left x=rsinthetacosphi\ y=rsinthetasinphi\ z=rcosthetaendright.$

УРАВНЕНИЕ СФЕРЫ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ
$(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=R^2$

где сфера имеет центр $(x_0,y_0,z_0)$ и радиус $R$.

УРАВНЕНИЕ СФЕРЫ В ЦИЛИНДРИЧЕСКИХ КООРДИНАТАХ
$r^2-2r_0r(theta-theta_0)+r_0^2+(z-z_0)^2=R^2$

где сфера имеет центр $(r_0;theta_0;z_0)$ в цилиндрических координатах и радиус $R$.

Если центр находится в начале координат, уравнение имеет вид:

УРАВНЕНИЕ СФЕРЫ В СФЕРИЧЕСКИХ КООРДИНАТАХ
$r^2+r_0^2-2r_0 rsinthetasintheta_0cos(phi-phi_0)=R^2$

где сфера имеет центр $(r_0; theta_0; phi_0)$ в сферических координатах и радиус $R$.

Если центр в начале координат, уравнение имеет вид:

ЭЛЛИПТИЧЕСКИЙ ЦИЛИНДР С ОСЬЮ КАК $z$ ОСЬ
$frac +frac =1$

Обратите внимание на ориентацию осей этой фигуры.

Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

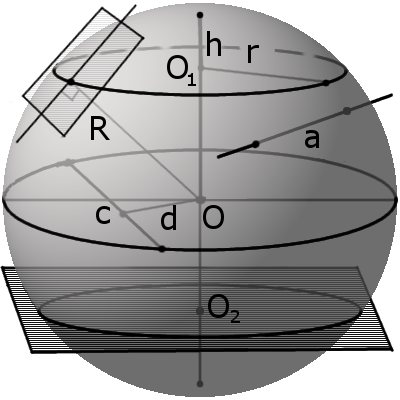
Сфера, шар, сегмент и сектор. Формулы и свойства сферы

Формула. Объём шара:

V =	4	π R 3 =	1	π D 3
	3		6

S = 4 π R 2 = π D 2

Видео:Уравнение окружности (1)Скачать

Уравнение сферы

x 2 + y 2 + z 2 = R 2

( x — x ₀) 2 + ( y — y ₀) 2 + ( z — z ₀) 2 = R 2

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Основные свойства сферы и шара

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Секущая, хорда, секущая плоскость сферы и их свойства

d m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m r такого круга можно найти по формуле:

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Видео:Полярная система координатСкачать

Касательная, касательная плоскость к сфере и их свойства

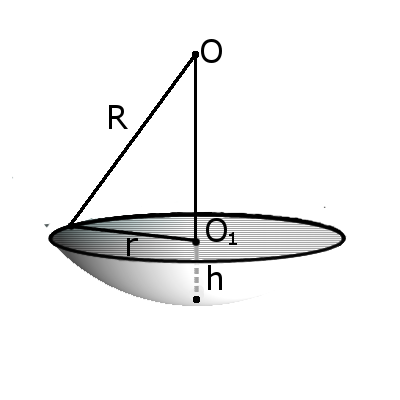
Формула. Объём сегмента сферы с высотой h через радиус сферы R:

V =	h 2 π	(3R — h )
	3

S = π R(2 h + √ 2 h R — h 2 )

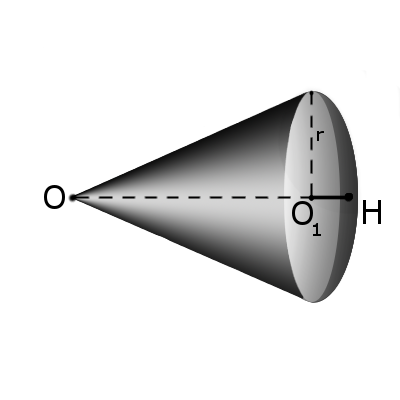
Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

V =	2 π R 2 h
	3

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Видео:Скорость и ускорение точки в полярных координатахСкачать

Уравнение окружности в сферических координатах

Декартова система координат хорошо известна. И всё же сформулируем подробнее, каким образом она задаётся на плоскости, и какие величины в результате однозначно определяют положение точки на плоскости. Не будем, однако, слишком углубляться в терминологию, т.к. используемые понятия просты и подробно изучаются в курсе средней школы.

Как уже было замечено в гл.1, § 6, задать декартову систему координат на плоскости означает зафиксировать, во-первых, точку начала координат, а во-вторых, две перпендикулярные направленные оси (так называемые, оси координат). Причём, эти оси занумерованы. И, конечно, понадобится единичный отрезок, чтобы численно обозначать расстояние между двумя точками.

Таким образом, положение любой точки на плоскости однозначно определено двумя числами: первое число – величина проекции точки на первую ось (взятая с плюсом, если проекция попала на “положительную” часть оси, или с минусом, если на “отрицательную”), а второе – величина проекции на вторую ось.

Стандартным образом декартова система координат обозначается Oxy, оси нумеруются таким образом, что поворот от первой оси ко второй осуществляется против часовой стрелки. Координаты точки – (x,y).

Для того, чтобы задать полярную систему координат на плоскости, надо зафиксировать, во-первых, точку начала координат, а во-вторых, луч, выходящий из этой точки. Необходимо также определить единичный отрезок и положительное направление отсчета угла между лучом и отрезком, соединяющим начало координат с какой-либо точкой плоскости.

Положение точки на плоскости задаётся двумя числами. Первое – расстояние от точки до начала координат, а второе – угол между зафиксированным лучом и отрезком, соединяющим точку и начало координат.

Обычно направление отсчета угла выбирают против часовой стрелки. Стандартное обозначение координат точки в полярной системе – (ρ ,φ) . Очевидно, ρ0.

Существуют формулы перехода между заданными стандартным образом декартовой и полярной системами координат. Если они друг другу соответствуют (т.е. должны совпадать начала координат в обеих системах, луч полярной системы координат должен совпадать с “положительной” частью первой оси декартовой системы, должны быть одинаковыми единичные отрезки), то

В других случаях формулы зависят от постановки задачи, но получить их легко из геометрических соображений.

С помощью этих формул можно осуществлять переход между двумя системами координат, преобразовывать координаты точек, уравнения кривых и т.д..

В полярной системе координат очень просто выглядят уравнения прямых, проходящих через начало координат и окружностей с центром в этой точке. Кроме того, уравнения многих стандартных, часто используемых, кривых принято (с точки зрения простоты) записывать в полярных координатах.

Пример 1. Найти полярные координаты точки с заданными декартовыми координатами.

Пример 2. Найти декартовы координаты точки с заданными полярными координатами.

Декартовы координаты в пространстве задаются с помощью точки начала координат и трёх взаимно-перпендикулярных направленных прямых. Прямые занумерованы, задан единичный отрезок. Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.

Цилиндрическая система координат в пространстве – “родственница” полярной системы координат на плоскости. Чтобы получить цилиндрическую систему надо на плоскости ввести полярную систему координат и добавить вертикальную координатную ось. Т.о., координаты точки – три числа: первые два – полярные координаты проекции нашей точки на плоскость, третье – величина проекции точки на вертикальную ось.

Из геометрических соображений можно получить формулы перехода между цилиндрической и декартовой системами координат. В случае, изображённом на рисунке, формулы перехода такие:

Пример 3. В декартовой системе координат поверхность задана уравнением . Перепишем это уравнение в цилиндрической системе координат.

Сферическая система координат вводится следующим образом: фиксируем плоскость, на ней — точку О начала координат, а из точки О выпускаем луч, перпендикулярный плоскости, и луч, лежащий в плоскости. Положение точки М задаётся тремя числами: первое – расстояние от начала координат О до точки М; второе – угол между проекцией отрезка ОМ на плоскость и лежащим в плоскости лучом; третье – угол между перпендикулярным плоскости лучом и отрезком ОМ.

Из геометрических соображений можно получить формулы перехода между сферической и декартовой системами координат. В случае, изображённом на рисунке, формулы перехода такие: