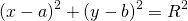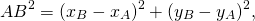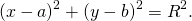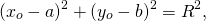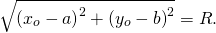Уравнение окружности в прямоугольных координатах

Видео:Уравнение окружности (1)Скачать

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Видео:Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

что и требовалось доказать.

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Уравнение окружности

Уравнение окружности с центром в точке (a;b) и радиусом R в прямоугольной системе координат имеет вид

1. Пусть в прямоугольной системе координат задана окружность с центром в точке A (a;b) и радиусом R (R>0).

Чтобы составить уравнение этой окружности, выберем на окружности произвольную точку B (x;y).

По определению окружности, расстояние от центра до любой точки окружности равно радиусу R, то есть AB=R.

Так как B (x;y) — произвольная точка окружности, координаты любой точки окружности удовлетворяют этому уравнению.

2. Если пара чисел (x_o;y_o) удовлетворяет данному уравнению, то

А это значит, что расстояние между точками C(x_o;y_o) и A(a;b) равно R. Значит, точка C(x_o;y_o) принадлежит окружности с центром в точке A(a;b) и радиусом R.

Следовательно, данное уравнение фигуры является уравнением окружности.

Видео:§2 Различные уравнения окружностиСкачать

Окружность уравнение окружности в прямоугольных декартовых координатах

Видео:Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

Декартовы координаты точек плоскости. Уравнение окружности

Числовая ось

Прямоугольная декартова система координат на плоскости

Формула для расстояния между двумя точками координатной плоскости

Уравнение окружности на координатной плоскости

Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Числовая ось

Определение 1 . Числовой осью ( числовой прямой, координатной прямой ) Ox называют прямую линию, на которой точка O выбрана началом отсчёта (началом координат) (рис.1), направление

указано в качестве положительного направления и отмечен отрезок, длина которого принята за единицу длины.

Определение 2 . Отрезок, длина которого принята за единицу длины, называют масштабом .

Каждая точка числовой оси имеет координату , являющуюся вещественным числом. Координата точки O равна нулю. Координата произвольной точки A , лежащей на луче Ox , равна длине отрезка OA . Координата произвольной точки A числовой оси, не лежащей на луче Ox , отрицательна, а по абсолютной величине равна длине отрезка OA .

Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Прямоугольная декартова система координат на плоскости

Определение 3 . Прямоугольной декартовой системой координат Oxy на плоскости называют две взаимно перпендикулярных числовых оси Ox и Oy с одинаковыми масштабами и общим началом отсчёта в точке O , причём таких, что поворот от луча Ox на угол 90° до луча Oy осуществляется в направлении против хода часовой стрелки (рис.2).

Замечание . Прямоугольную декартову систему координат Oxy , изображённую на рисунке 2, называют правой системой координат , в отличие от левых систем координат , в которых поворот луча Ox на угол 90° до луча Oy осуществляется в направлении по ходу часовой стрелки. В данном справочнике мы рассматриваем только правые системы координат, не оговаривая этого особо.

Если на плоскости ввести какую-нибудь систему прямоугольных декартовых координат Oxy , то каждая точка плоскости приобретёт две координаты – абсциссу и ординату, которые вычисляются следующим образом. Пусть A – произвольная точка плоскости. Опустим из точки A перпендикуляры AA₁ и AA₂ на прямые Ox и Oy соответственно (рис.3).

Определение 4 . Абсциссой точки A называют координату точки A₁ на числовой оси Ox , ординатой точки A называют координату точки A₂ на числовой оси Oy .

Обозначение . Координаты (абсциссу и ординату) точки A в прямоугольной декартовой системе координат Oxy (рис.4) принято обозначать A (x ; y) или A = (x ; y).

Замечание . Точка O , называемая началом координат , имеет координаты O (0 ; 0) .

Определение 5 . В прямоугольной декартовой системе координат Oxy числовую ось Ox называют осью абсцисс , а числовую ось Oy называют осью ординат (рис. 5).

Определение 6 . Каждая прямоугольная декартова система координат делит плоскость на 4 четверти ( квадранта ), нумерация которых показана на рисунке 5.

Определение 7 . Плоскость, на которой задана прямоугольная декартова система координат, называют координатной плоскостью .

Замечание . Ось абсцисс задаётся на координатной плоскости уравнением y = 0 , ось ординат задаётся на координатной плоскости уравнением x = 0.

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Формула для расстояния между двумя точками координатной плоскости

Утверждение 1 . Расстояние между двумя точками координатной плоскости

вычисляется по формуле

Доказательство . Рассмотрим рисунок 6.

что и требовалось доказать.

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнение окружности на координатной плоскости

Поскольку расстояние от любой точки окружности до центра равно радиусу, то, в соответствии с формулой (1), получаем:

Уравнение (2) и есть искомое уравнение окружности радиуса R с центром в точке A₀ (x₀ ; y₀) .

Следствие . Уравнение окружности радиуса R с центром в начале координат имеет вид

Видео:Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

Уравнение окружности

Уравнение окружности с центром в точке (a;b) и радиусом R в прямоугольной системе координат имеет вид

1. Пусть в прямоугольной системе координат задана окружность с центром в точке A (a;b) и радиусом R (R>0).

Чтобы составить уравнение этой окружности, выберем на окружности произвольную точку B (x;y).

По определению окружности, расстояние от центра до любой точки окружности равно радиусу R, то есть AB=R.

Так как B (x;y) — произвольная точка окружности, координаты любой точки окружности удовлетворяют этому уравнению.

2. Если пара чисел (x_o;y_o) удовлетворяет данному уравнению, то

А это значит, что расстояние между точками C(x_o;y_o) и A(a;b) равно R. Значит, точка C(x_o;y_o) принадлежит окружности с центром в точке A(a;b) и радиусом R.

Следовательно, данное уравнение фигуры является уравнением окружности.

Видео:Площадь фигуры через двойной интеграл в полярных координатахСкачать

Уравнение окружности

Общее уравнение окружности записывается как:

Точка — центр окружности, R — её радиус.

Уравнение окружности радиуса R с центром в начале координат:

Уравнение окружности, проходящей через три точки (с помощью определителя) ,

Окружность также можно описать с помощью параметрического уравнения:

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:

Если центр окружности совпадает с началом координат, функции принимают вид:

Видео:Полярная система координатСкачать

Перенос начала координат

В аналитической геометрии основное значение имеет так называемая задача преобразования координат. Она заключается в следующем. Даны две системы координат (на плоскости или в пространстве) — «старая» и «новая». Требуется, зная координаты какой-нибудь точки или вектора в одной системе координат, найти координаты той же точки или вектора в другой системе.

Предположим, что даны две координатные системы, у которых одни и те же единичные векторы, но разные начала О и О’, так что новая система координат О’ получается из старой О, сдвигом на вектор ОО’ (рисунок представлен ниже).

При этом даны координаты точки О’ относительно системы О е₁ е₂ : О’ = (a, b). Мы уже знаем, что в этом случае координаты каждого вектора u в обеих системах одинаковы, потому что этими координатами являются координаты вектора u относительно одного и того же базиса, т.е. коэффициенты x, y в представлении

u = xe₁ + ye₂.

Посмотрим, как связаны между собою координаты x, y и x’, y’ произвольной точки М в обеих системах. Числа x, y суть координаты вектора ОМ (рисунок представлен ниже), а числа x’, y’- координаты вектора О’М (относительно того же базиса е₁ е₂). Но

Причем для вектора ОМ, ОО’, О’М (и базиса е₁ е₂) имеем

Так что векторное равенство (1) равносильно совокупности двух числовых равенств:

Эти формулы и решают поставленную задачу.

В случае плоскости вместо трех равенств (2) получаем два: если координаты нового начала О’ относительно старой системы координат суть a, b,так что O’ = (a, b) в старой системы координат, то координаты x, y произвольной точки М в старой системе выражаются через координаты той же точки в новой системе формулами:

Иногда при решении задач удобно вместо данной системы XOY использовать другую X’O’Y’, определенным образом ориентированную относительно данной системы.

Пусть новая система X’O’Y’ получена из старой ХОY параллельным переносом осей координат, т.е. оси новой системы параллельны осям старой и имеют одинаковое с ними направление (Рисунок представлен ниже). Пусть начало О’ новой системы имеет координаты (a, b) в старой системе.

Возьмем точку М на плоскости и найдем зависимость между ее координатами (х, у) в старой системе и (х’, у’) в новой. Из рисунка ясно, что

Если уравнение не содержит члена с произведением координат (В= 0), то с помощью параллельного переноса оно приводится к каноническому виду. Для этого необходимо в случае А ? 0, С ? 0 выделить полные квадраты для членов, содержащих у, и членов, содержащих х, затем для полученных полных квадратов вида (х — а) 2 , (y — b) 2 .

🔥 Видео

№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Уравнение окружности в декартовых координатахСкачать

Уравнение окружностиСкачать

§12 Полярное уравнение прямойСкачать