Уравнение окружности касающейся оси координат

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Уравнение окружности касающейся оси координат

Составить уравнение окружности, проходящей через точку A (2; 1) и касающейся осей координат.

Пусть (a; 0) — координаты точки касания окружности с осью Ox. Тогда (см. рисунок) точка касания окружности с осью Oy имеет координаты (0; a), центр окружности имеет координаты (a; a) и радиус окружности равен a, поскольку окружность проходит через точку A(2; 1), у которой каждая координата больше нуля. Это означает, что окружность расположена в I квадранте, в котором a > 0.

Следовательно, уравнение окружности имеет вид (x — a) 2 + (y — a) 2 = a 2 .

Так как окружность проходит через точку A(2; 1), то имеем (2 — a) 2 + (1 — a) 2 = a 2 , откуда a = 1 или a = 5.

Искомое уравнение окружности: (x — 1) 2 + (y — 1) 2 = 1 или (x — 5) 2 + (y — 5) 2 = 25.

Видео:Уравнение окружности (1)Скачать

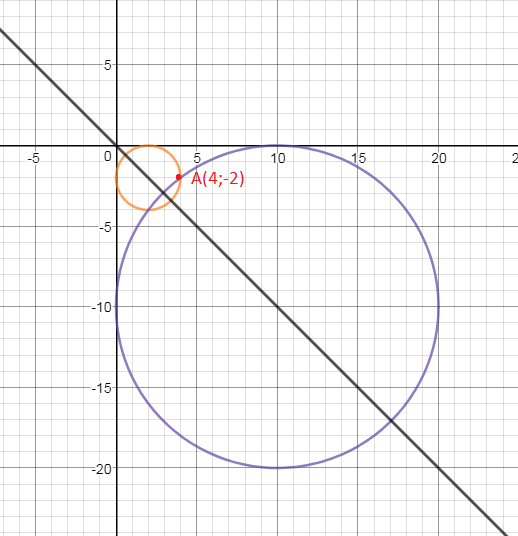
Задача 28098 4.3.4) Найти уравнение окружности.

Условие

4.3.4) Найти уравнение окружности, касающейся осей координат и проходящей через точку (4; -2).

Решение

Окружность касается осей координат и проходит через точку, расположенную в четвертой координатной четверти, значит центр окружности лежит на биссектрисе второго и четвертого координатных углов, т.е на прямой y = — x.
и потому центр окружности имеет координаты (R;-R)

Следовательно, уравнение окружности имеет вид
(x — R)^2 + (y -(- R))^2 = R^2.

Поскольку точка A(4;-2) лежит на окружности, координаты этой точки удовлетворяют полученному уравнению,
т.е.
(4 — R)^2 + (-2 + R)^2 = R^2.
16-8R+R^2+4-4R+R^2=R^2
R^2-12R+20=0
D=144-80=64
R=2 или R=10

(x — 2)^2 + (y+2)^2 = 4 или
(x — 10)^2 + (y+10)^2 = 100

.

Видео:Составьте уравнение окружности, касающейся осей координат и проходящей через точку M(2;-1)Скачать

Окружность касается оси ох в начале координат

Видео:Уравнение окружностиСкачать

Окружность касается оси ох в начале координат

Найти уравнение окружности, касающейся оси Ox в начале координат и пересекающей ось Oy в точке A(0, 10).

Известно, что диаметр окружности, проведенной в точку касания, перпендикулярен касательной. Это значит, что диаметр AO окружности направлен по оси Oy, центр окружности находится в точке C(0, 5), а радиус окружности r = 5. Искомое уравнение имеет вид x 2 + (y — 5) 2 = 25, или x 2 + y 2 — 10y = 0.

Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Окружность касается оси абцисс в начале координат и проходит через точку(0 ; — 4)?

Алгебра | 10 — 11 классы

Окружность касается оси абцисс в начале координат и проходит через точку(0 ; — 4).

Составить уравнение этой окружности и найти её точки пересечения с биссектрисами координатных углов.

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций :

y = yo + — V(R ^ 2 — (x — xo) ^ 2).

Примечание — V — это знак корня квадратного.

Если окружность касается оси абсцисс в начале координат и проходит через точку(0 ; — 4), то радиус её равен 4 / 2 = 2, а координаты её центра :

Уравнение этой окружности будет иметь вид : y = — 2 + — V(4 — x ^ 2).

Уравнения биссектрис координатных углов у = х и у = — х, если решить совместно эти уравнения, получим координаты точек пересечения с биссектрисами координатных углов :

это( — 2 ; — 2) и (2 ; — 2).

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Составьте уравнение окружности с центром в точке ( — 4 ; — 6), касающейся оси х?

Составьте уравнение окружности с центром в точке ( — 4 ; — 6), касающейся оси х.

Видео:Уравнение окружности ? Окружность в системе координат / Функция окружностиСкачать

Центр окружности А(4?

Центр окружности А(4.

Найдите координаты точек пересечения этой окружности с координатными осями.

Видео:№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

Найти угол АСО если сторона СА касается окружности в точке А?

Найти угол АСО если сторона СА касается окружности в точке А.

О — центр окружности, отрезок ОС пересекает окружность в точке В, а меньшая дуга окружности АВ, заключенная внутри этого угла равна 58° Ответ дайте в градусах.

Видео:УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать

Найдите центр и радиус окружности, заданной уравнением (выше)?

Найдите центр и радиус окружности, заданной уравнением (выше).

И найдите точки пересечения этой окружности с осями координат.

Видео:Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

Напишите уравнение окружности с центром в точке(2 ; — 3), если окружность касается оси абсцисс?

Напишите уравнение окружности с центром в точке(2 ; — 3), если окружность касается оси абсцисс.

Видео:ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Напишите уравнение окружности с центром в начале координат, если известно, что она проходит через точку A(5 ; 12)?

Напишите уравнение окружности с центром в начале координат, если известно, что она проходит через точку A(5 ; 12).

Видео:УРАВНЕНИЯ ОКРУЖНОСТИ И ПРЯМОЙ 9 класс геометрияСкачать

Найдите координаты точки пересечения графика функции y = — 2x — 14 с осью абцисс?

Найдите координаты точки пересечения графика функции y = — 2x — 14 с осью абцисс.

Видео:№970. Напишите уравнение окружности, проходящей через точку А (1; 3), если известноСкачать

Составmте уравyение окружности зная что она касается оси OX в начале координат и пересекает ось OYв точке А(0, 4)?

Составmте уравyение окружности зная что она касается оси OX в начале координат и пересекает ось OYв точке А(0, 4).

Видео:№971. Напишите уравнение окружности, проходящей через точки А (-3; 0) и B (0; 9), если известноСкачать

Найдите координаты точки пересечения графика функции у = — 2х — 14 с осью абцисс?

Найдите координаты точки пересечения графика функции у = — 2х — 14 с осью абцисс.

Видео:Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

Точка А(3 ; — 2) — центр окружности радиусом 3 ?

Точка А(3 ; — 2) — центр окружности радиусом 3 .

Найдите координату точки пересечения окружности с осью Оу .

Вы открыли страницу вопроса Окружность касается оси абцисс в начале координат и проходит через точку(0 ; — 4)?. Он относится к категории Алгебра. Уровень сложности вопроса – для учащихся 10 — 11 классов. Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие ответы по интересующей теме. Чтобы получить наиболее развернутый ответ, можно просмотреть другие, похожие вопросы в категории Алгебра, воспользовавшись поисковой системой, или ознакомиться с ответами других пользователей. Для расширения границ поиска создайте новый вопрос, используя ключевые слова. Введите его в строку, нажав кнопку вверху.

Х = 2 + 2 х = 4 ответ : 4.

3аx = — 45 Если x = 3, то 3×а×3 = — 45 = 9а = — 45 Решаем уравнение 9а = — 45 a = — 45÷9 a = — 5 При значении а = — 5.

В данное уравнение вместо х подставляем 3 и решаем новое уравнение. 3 * а * 3 = — 45 9 * а = — 45 а = — 45 : 9 а = — 5 Ответ : при а = — 5.

13 — t + 17 — (t — 18 + 14) = 13 — t + 17 — t + 18 — 14 = 34.

X + x / 12 = — 13 / 6 12x / 12 + x / 12 + 26 / 12 = 0 x + 12 + 26 = 0 13x = — 26 x = — 2.

1) = 2)121 / 11 = 11.

9√64 * 18√64 = 9 * 18 * √64² = 9 * 18 * 64 = 10368 Log₃121 / log₃11 = log₁₁121 = log₁₁11² = 2.

Х км / ч — собственнаяскорость теплохода (х + 4) км / ч — скорость теплохода потечению (х — 4) км / ч — скорость теплохода противтечения 180 км — расстояние, которое теплоход проходит по течению реки и это же расстояние он проходит против течения 180..

Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Если окружность касается оси ох

Видео:9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Если окружность касается оси ох

Найти уравнение окружности, касающейся оси Ox в начале координат и пересекающей ось Oy в точке A(0, 10).

Известно, что диаметр окружности, проведенной в точку касания, перпендикулярен касательной. Это значит, что диаметр AO окружности направлен по оси Oy, центр окружности находится в точке C(0, 5), а радиус окружности r = 5. Искомое уравнение имеет вид x 2 + (y — 5) 2 = 25, или x 2 + y 2 — 10y = 0.

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Касательная к окружности

О чем эта статья:

Касательная к окружности, секущая и хорда — в чем разница

В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.

Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.

Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).

Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.

Свойства касательной к окружности

Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.

Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.

Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:

• окружность с центральной точкой А;
• прямая а — касательная к ней;
• радиус АВ, проведенный к касательной.

Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.

Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.

В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.

Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Задача

У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.

Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.

Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.

∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°

Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.

Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.

Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.

Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.

Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.

Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.

Задача 1

У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.

Решение

Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.

∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).

Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:

∠BDC = ∠BDA × 2 = 30° × 2 = 60°

Итак, угол между касательными составляет 60°.

Задача 2

К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.

Решение

Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.

Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.

∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°

Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.

Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.

Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.

Задача 1

Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.

Решение

Исходя из соотношения касательной и секущей МА 2 = МВ × МС.

Найдем длину внешней части секущей:

МС = МВ — ВС = 16 — 12 = 4 (см)

МА 2 = МВ × МС = 16 х 4 = 64

Задача 2

Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.

Решение

Допустим, что МО = у, а радиус окружности обозначим как R.

В таком случае МВ = у + R, а МС = у – R.

Поскольку МВ = 2 МА, значит:

МА = МВ : 2 = (у + R) : 2

Согласно теореме о касательной и секущей, МА 2 = МВ × МС.

(у + R) 2 : 4 = (у + R) × (у — R)

Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:

Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).

Ответ: MO = 10 см.

Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.

Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.

Задача 1

Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.

Решение

Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.

АВ = ∠АВС × 2 = 32° × 2 = 64°

Задача 2

У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.

Решение

Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:

КМ = 2 ∠МКВ = 2 х 84° = 168°

Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.

∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2

Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:

∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°