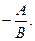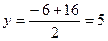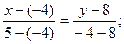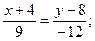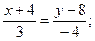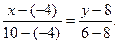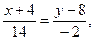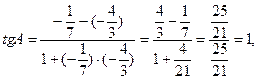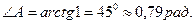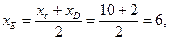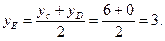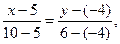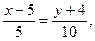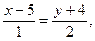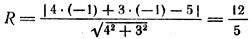Уравнение окружности для которой есть диаметр

Видео:9 класс, 6 урок, Уравнение окружностиСкачать

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Видео:Уравнение окружности (1)Скачать

Уравнение окружности для которой высота сd есть диаметр

Видео:№969. Напишите уравнение окружности с диаметром MN, если: а) М (-3; 5),Скачать

ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

НА ПЛОСКОСТИ

1. Метод координат. Виды уравнений прямой на плоскости.

2. Взаимное расположение 2 – х прямых на плоскости. Угол между 2 – мя прямыми. Условие параллельности и перпендикулярности 2 – х прямых на плоскости.

3. Кривые 2 – го порядка: окружность, эллипс, парабола, гипербола.

Решение типового примера

Пример 3.1.

Даны координаты вершин треугольника ABC: A(4; 3), B(16; — 6), C(20; 16). Найти

1) длину стороны АВ:

(1)

Применяя (1), находим длину стороны АВ:

2) уравнения сторон АВ и ВС и их угловые коэффициенты:

(2)

является уравнением прямой, проходящей через две точки

Подставляя в (2) координаты точек A и B, получим уравнение прямой АВ:

; ; 4y-12=-3x+12; или 3x+4y -24=0 (АВ).

называется уравнением прямой с угловым коэффициентом; k — угло­вой коэффициент, b — величина отрезка, ко­торый отсекает прямая на оси Оу, считая от начала координат.

Если прямая задана общим уравнением Ах+Ву+С=0, то её угловой коэффициент определяется по формуле k =

Решив последнее уравнение относительно y, находим уравнение стороны АВ в виде уравнения прямой с угловым коэффициентом:

4y =-3x+24, или y = — x+6, откуда k _АВ =

Аналогичным образом, подставляя координаты точек B и C в (2), находим уравнение прямой BC: 11x- 2y -188=0 (ВС) откуда k _ВС =

Если известны угловые коэффициенты двух прямых k₁ и k₂, то один из углов φ между этими прямыми определяется по формуле

(3)

Искомый угол В образован прямыми АВ и BC, угловые коэффициенты которых известны из предыдущего пункта. Применяя (3), получим

= 2.

4) уравнение медианы АЕ:

Определим координаты точки Е, которая является серединой отрезка BC по формулам координат середины данного отрезка:

, (4)

Имеем для точки Е: ,
Таким образом, Е(18; 5).

Подставляя в (2) координаты точек А и Е, находим уравнение медианы АЕ:

; ; x-7y +17=0 (АЕ).

5) уравнение и длину высоты СД:

является уравнением прямой, которая проходит через точку М₀ (х₀ ; у₀) и имеет угловой коэффициент k.

Высота СД перпендикулярна стороне АВ. Воспользуемся условием перпендикулярности 2 – х прямых на плоскости. Признаком перпендикулярности двух прямых является соотношение

k₁k₂= —1 или k₂= —

Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку. Отсюда

k_CD= — =

Подставив в (5) координаты точки С и k_CD получим уравнение высоты СD:

у — 16 = (x—20); 4x-3y -32=0 (СD).

Для нахождения длины высоты СD определим координаты точки D как точки пересечения прямых АВ и СD, решив совместно систему уравнений, их задающих:

6) уравнение окружности, для которой высота СD есть диаметр;

Уравнение окружности с центром в точке О(а; b) радиуса R имеет вид:

(x-a) 2 +(y-b) 2 =R 2 (6)

Если СD есть диаметр, то центр окружности – точка О – есть середина СD . Используя формулы (4) имеем для О:

, ,

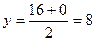
Таким образом, О(14; 8).

Если СD есть диаметр, то радиус окружности – есть отрезок СО . Используя (1) найдем радиус:

R=

Тогда, (x-14) 2 +(y-8) 2 =80 – уравнение искомой окружности.

7) уравнение прямой, проходящей через точку Е параллельно стороне

АВ, и точку K ее пересечения с высотой СD:

Т.к. заданная прямая параллельна стороне АВ, то можем использовать условие параллельности 2 – х прямых на плоскости: Признаком параллельности двух прямых является равенство их угловых коэффициентов

т.е. k = k_AB = —3/4. Знаем, что прямая проходит через точку Е с заданным угловым коэффициентом. Можем использовать уравнение (5):

Точку K пересечения EL с высотой СD найдем, решив совместно систему уравнений, задающих эти прямые:

8) систему линейных неравенств, определяющих треугольник АВС:

Используя неравенство треугольника (сумма двух любых сторон треугольника меньше третьей его стороны), получаем систему:

Из п. 2 известны 3x+4y -24=0 (АВ), 11x- 2y -188=0 (ВС). Запишем уравнение АС, используя (2):

; ; 13(x-4)=16(y-3); 13x-16y-4=0 (АС).

Тогда, система линейных неравенств, определяющих треугольник АВС примет вид:

Или

Задачи контрольной работы

В задачах 3.1.1- 3.1.20 даны координаты вершин треугольника АВС. Найти:

· длину стороны АВ;

· уравнения сторон АВ и ВС и их угловые коэффициенты;

· угол B в радианах;

· уравнение медианы АЕ;

· уравнение и длину высоты СД;

· уравнение окружности, для которой высота СД есть диаметр;

· уравнение прямой, проходящей через точку Е параллельно стороне

АВ, и точку ее пересечения с высотой СД;

· систему линейных неравенств, определяющих треугольник АВС.

Решение типового примера

Пример 3.2. Определить вид кривой, построить, найти координаты фокусов и эксцентриситет:

Пусть дана кривая .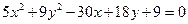

Решение:

Приведем данное уравнение к каноническому виду. Для этого сгруппируем отдельно члены, содержащие переменные и :

.

В каждой из скобок вынесем коэффициент при квадрате переменной, а затем выделим полный квадрат, используя формулы сокращенного умножения :

.

Первые три слагаемые в скобках образуют полный квадрат разности , следовательно

.

Аналогичные действия осуществим для переменной :

.

Первые три слагаемые в скобках образуют полный квадрат суммы , следовательно

.

Тогда исходное уравнение примет вид:

,

,

.

Введем обозначения: . Произведенную замену будем рассматривать, как преобразование декартовых координат в координаты при параллельном сдвиге координатных осей. Причем новое начало координат находится в точке . В этой системе координат наше уравнение примет вид:

.

Это каноническое уравнение эллипса. Его полуоси . Кроме того, , следовательно эксцентриситет . остается найти координаты вершин и фокусов эллипса. В новой системе координаты вершин таковы: ; координаты фокусов . Так как старые координаты выражаются через новые по формулам , то, возвращаясь к первоначальной системе координат получим: , .

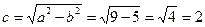
Видео:начертить окружность. Привести уравнение окружности к стандартному виду. Координаты центра и радиус.Скачать

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Видео:УРАВНЕНИЕ ОКРУЖНОСТИСкачать

Элементы линейной алгебры, аналитической геометрии и линейного программирования

Элементы линейной алгебры, аналитической геометрии и линейного программирования — раздел Математика, Продемонстрировать эффективность применения изучаемых математических методов в туристической индустрии По Теме «Аналитическая Геометрия» Рассмотрим Решение Типовой Задачи. .

По теме «Аналитическая геометрия» рассмотрим решение типовой задачи.

Задача 1. Даны вершины треугольника АВС: А(-4;8), В(5;-4), С(10;6).

1) длину стороны АВ;

2) уравнения сторон АВ и АС и их угловые коэффициенты;

3) угол А в радианах;

4) уравнение высоты СD и ее длину;

5) уравнение окружности, для которой высота СD есть диаметр;

6) систему линейных неравенств, определяющих треугольник АВС.

1. Найдем длину стороны АВ.

. (1)

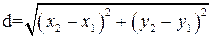
Подставив в эту формулу координаты точек А и В, имеем:

АВ=.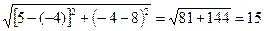

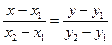
(2)

Подставив в (2) координаты точек А и В, получим уравнение прямой АВ:

Для нахождения углового коэффициента к_АВ прямой АВ, разрешим полученное уравнение относительно у: у = .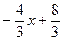

Отсюда к_АВ =.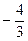

Подставив в формулу (2) координаты точек А и С, найдем уравнение прямой АС:

Отсюда к_АС =.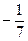

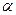
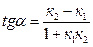
3. Угол между двумя прямыми, угловые коэффициенты которых равны к₁ и к₂, определяется по формуле:

(3)

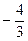
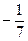
Угол А, образованный прямыми АВ и АС, найдем по формуле (3), подставив в нее к₁ = к_АВ = , к₁ = к_АС =.

4. Так как высота СD перпендикулярна стороне АВ, то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.

к_СD = .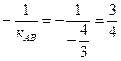

Уравнение прямой, проходящей через данную точку М₁(х₁; у₁) в заданном направлении, имеет вид:

(4)

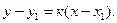
Подставив в (4) координаты точки С(10;6) и к_СD = 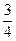, получим уравнение высоты СD:

у – 6 = 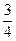(х – 10), 4у – 24 = 3х – 30, 3х – 4у – 6 = 0 (СD). (5)

Для нахождения длины СD определим координаты точки D, решив систему уравнений (АВ) и (CD):

, откуда х = 2, у = 0, то есть D (2; 0).

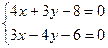
Подставив в формулу (1) координаты точек С и D, находим:

СD =.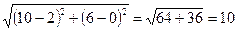

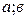
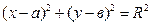
5. Уравнение окружности радиуса R с центром в точка Е() имеет вид:

(6)

Так как СD является диаметром искомой окружности, то ее центр Е есть середина отрезка СD. Воспользуемся формулами деления отрезка пополам, получим:

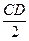
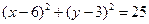
Следовательно, Е(6; 3) и R = = 5. Используя формулу (6), получаем уравнение искомой окружности:

.

6. Множество точек треугольника АВС есть пересечение трех полуплоскостей, первая из которых ограничена прямой АВ и содержит точку С, вторая ограничена прямой ВС и содержит точку А, а третья ограничена прямой АС и содержит точку В.

Для получения неравенства, определяющего полуплоскость, ограниченную прямой АВ и содержащую точку С, подставим в уравнение прямой АВ координаты точки С:

> 0.

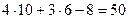
Поэтому искомое неравенство имеет вид: 4х+3у .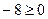

Для составления неравенства, определяющего полуплоскость, ограниченную прямой ВС и содержащую точку А, найдем уравнение прямой ВС, подставив в формулу (2) координаты точек В и С:

(ВС).

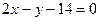
Подставив в последнее уравнение координаты точки А, имеем:

Развернуть

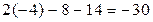
Эта тема принадлежит разделу:

Продемонстрировать эффективность применения изучаемых математических методов в туристической индустрии

Высшего профессионального образования города москвы.. московский государственный институт индустрии туризма имени ю а сенкевича..

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Элементы линейной алгебры, аналитической геометрии и линейного программирования

Видео:Составить уравнение окружности. Геометрия. Задачи по рисункам.Скачать

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Организационно-учебные нормы
Название контрольной точки Срок сдачи Срок проверки Первое задание – выполнить конт­ро

Тематический план изучения дисциплины, 1 семестр
Тема Виды учебных занятий Всего Ауд. работа Самостоя­тельные занятия

Матричный метод решения системы линейных уравнений
Рассмотрим систему линейных уравнений (1) Обозначим через А – матрицу

Дифференциальное и интегральное исчисление
Исследование функций и построение графиков рекомендуется проводить по следующей схеме: 1) Найти область определения функции. 2) Исследовать функцию на непрерывность; найти точки р

Элементы теории вероятностей
Случайное событие, называемое также событием, – это такое явление, которое может либо произойти, либо не произойти в результате испытания. Классическое определение вероятнос

Случайные величины
Случайной величиной называется величина, которая в результате испытания принимает одной возможное числовое значение. Случайные величины (с.в.) обозначаются заглавными латинскими буквами.

Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

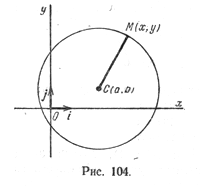
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = ( sqrt ), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

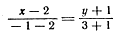
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

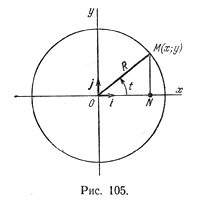
Пусть в прямоугольной системе координат дана окружность x 2 + у 2 = R 2 . Рассмотрим ее произвольную точку М(х; у) (рис. 105).

Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем

🔍 Видео

Радиус и диаметрСкачать

Составляем уравнение окружностиСкачать

ПРОСТОЙ СЕКРЕТ ДЛЯ НАЧИНАЮЩИХ! Реши алгебру за 12 минут — Уравнение ОкружностиСкачать

Уравнение окружностиСкачать

№967. Напишите уравнение окружности с центром в начале координат, проходящей через точку В (-1; 3).Скачать

ГЕОМЕТРИЯ 9 класс: Уравнение окружности и прямойСкачать

Всё про углы в окружности. Геометрия | МатематикаСкачать

Уравнение окружности | Геометрия 7-9 класс #90| ИнфоурокСкачать

Длина окружности. Математика 6 класс.Скачать

Длина окружности. Площадь круга. 6 класс.Скачать

УРАВНЕНИЕ ОКРУЖНОСТИ. ЗАДАНИЕ 18 (С5). АРТУР ШАРИФОВСкачать

Окружность, диаметр, хорда геометрия 7 классСкачать