1. Понятие регрессионного уравнения.
2. Метод наименьших квадратов.
3. Проверка адекватности регрессионного уравнения.
3.1. Показатели качества подгонки.
3.2. Проверка различных гипотез относительно регрессионного уравнения.
3.3. «Хорошие» свойства оценок.
3.4. Экономический смысл коэффициентов регрессии.
1. Регрессионное уравнение модели отражает зависимость между экономическими переменными, а именно между одной зависимой (эндогенной) и одной или более независимыми (экзогенными) переменными. Зависимая переменная обозначается через «у», а независимая через «х».
Направление причинно-следственной связи между переменными определяется через предварительное обоснование и включается в модель как гипотеза.
Регрессионный анализ проверяет статистическую состоятельность модели при данной гипотезе.
Регрессионное уравнение может быть однофакторным и многофакторным. В первом случае одна переменная зависит от другой, во втором случае одна переменная зависит от нескольких других.
Регрессионное уравнение, которое отражает зависимость между математическим ожиданием (условным распределением) одной переменной и соответствующим значением другой переменной, называется однофакторным регрессионным уравнением.
В общем виде однофакторное регрессионное уравнение может быть записано в следующем виде:
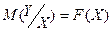
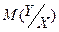
Частным случаем однофакторного регрессионного уравнения является линейная модель зависимости, которая записывается следующим образом:
yi=a+bxi+ 
yi – объяснимая (зависимая) переменная;
xi – объясняющая (независимая) переменная;
а – свободный член регрессии или постоянная;
b – коэффициент регрессии, отражает наклон линии, вдоль которой рассеяны данные наблюдения модели. Коэффициент регрессии может быть истолкован как показатель, характеризующий процентное изменение переменной, которым вызвано изменение значения х на единицу.
Если знак перед b положителен, то говорим, что переменные коррелированны положительно, при отрицательном знаке переменные отрицательно коррелированны.

1. любая регрессионная модель является упрощением действительной, на самом деле есть другие параметры, от которых зависит yi.
2. присутствуют ошибки измерений.
Необходимо различать кросс-секционную регрессию и регрессию временных рядов.
Кросс-секционная регрессия проверяет связь между переменными в определенный период времени. Например, зависимость между количеством работников предприятия и прибылью, полученной этим предприятием. Чтобы измерить эту связь мы должны собрать данные по численности работников за 1 период (например, год) и данные о размерах прибыли достаточно большого числа предприятий за тот же самый период.
Данные о прибылях компаний соответствовали бы зависимой переменной, а данные о количестве работников были бы независимыми переменными.
При анализе регрессии во временных рядах данные по каждой из переменных собираются в течение следующих друг за другом периодов времени.
Регрессионный анализ временных рядов позволяет установить взаимосвязь между переменными в среднем в течение того периода времени по которому имеются данные. Независимо от того проводится кросс-секционный анализ или анализ временных рядов, основные принципы положения регрессионного анализа остаются те же.
2.Для статистической проверки взаимозависимости между зависимой (у) и независимой (х) переменными, необходимо найти значения а, b, 
Метод оценки этих параметров должен быть таким, чтобы это были «хорошие» оценки.
Метод, используемый чаще других для нахождения параметров регрессионного уравнения и известный как метод наименьших квадратов дает наилучшие линейные несмещенные оценки. Метод называется так потому, что при расчете параметров линии с помощью этого метода минимизируются суммы квадратов значений ошибок 



 |  |
 |  |
 |  |
 |  |
 |
Допустим на графике нанесены наблюдения о совокупных доходах семей (х) и расходах этих же семей на питание (y). Анализируя графики можно сделать следующие выводы:
1. Точки не лежат на одной кривой и можно только провести некоторую линию в непосредственной близости от всех этих точек.
2. Можно сделать допущение, иными словами выдвинуть гипотезу, что доходы и расходы связаны линейной зависимостью, то есть можно построить некоторую прямую 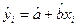
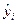
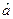
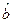
Для того, чтобы теоретическая прямая лежала в непосредственной близости от фактически наблюдаемых уi необходимо минимизировать сумму квадратов отклонений между фактическими и расчетными значениями.
Разрыв скобки получим стандартную форму нормальных уравнений (для краткости опустим индексы у знаков сумм).
из этой системы находим 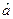
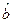
ковариация (cov) показывает тесноту связи
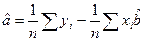
n – количество наблюдений.
Так рассчитываются величины регрессии.
Ошибка или случайная компонента 
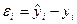
3. Адекватность регрессионного уравнения. То есть его соответствие реальному моделироваемому процессу, достоверность его параметров; исследуется с нескольких позиций:
1. Анализируются показатели качества подгонки регрессионного уравнения.
2. Проверяются различные гипотезы относительно параметров регрессионного уравнения.
3. Проверяется выполнение условий для получения «хороших» оценок МНК.
4. Производится содержательный анализ регрессионного уравнения.
3.1. Показатели качества подгонки отражают соотношение расчетных значений зависимой переменной 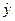
Эти показатели как правило основываются на сумме квадратов разности этих показателей:
Первый из таких показателей – остаточная дисперсия.
Для однофакторного уравнения однофакторная дисперсия определяется по формуле:
Чем меньше 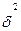
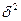
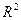
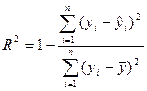
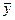
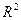
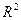
Этот показатель также независим от единиц измерения и характеризует силу и направление линейной связи между двумя переменными.
Значение коэффициента находится в интервале от (-1;1).
Если коэффициент близок к -1, то говорят об отрицательной линейной связи. Когда показатель близок к 0, то говорят о линейной независимости двух переменных. Когда показатель близок к 1 – о положительной линейной связи. При анализе коэффициентов корреляции необходимо учитывать, что коэффициент корреляции показывает только силу линейной связи.
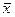
3.2. Приведенные ранее показатели качества подгонки не позволяют принять статистического решения по пригодности регрессионного уравнения, хотя и дают некоторое представление о качестве подгонки. Такие решения принимают на основе статистических критериев. Одним из таких критериев является F- критерий. Принятие решения на основе F-критерия опирается на общую процедуру проверки гипотезы. После оценки свободного члена регрессии и коэффициента регрессии выдвигается гипотеза о том, что линейная связь между x и y не подтверждается. Отсутствие связи можно изучить на основе отклонений расчетных значений 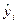
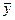
Близкое к 0 значение свидетельствует об отсутствии какой-либо тенденции для yi в связи с изменениями x. Строгое решение об опровержении линейной связи проверяется на основе F-статистики. Если F таб расч , то гипотезу об отсутствии линейной связи отвергаем с вероятностью p.
Значения F таб , берутся из таблицы критических точек распределения F (Фишера-Снедекора) для степеней свободы n1=1, n2=n-2.
Отдельно исследуется коэффициент регрессии b. Выдвигается гипотеза о том, что x влияет на y несущественно, то есть y изменяется по каким-то другим причинам, а не в связи с изменением x. Выдвинутая гипотеза равноценна тому, что b равен 0 для генеральной совокупности. Если наша гипотеза верна, то t-статистика подчиняется t-распределению со степенями свободы n-2.
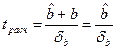
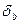
Если t расч >t табл , то с заданной вероятностью гипотезу о том, что b=0 отвергаем. t табл находится по таблице критических точек распределения Стьюдента с заданной вероятностью p b степенью свободы n-2. t-статистика используется также при построении доверительного интервала для коэффициента b.
Видео:Эконометрика. Линейная парная регрессияСкачать

ПОСТРОЕНИЕ ОДНОФАКТОРНОГО УРАВНЕНИЯ РЕГРЕССИИ
Читайте также:
|
│►12. Рассмотрим построение однофакторного уравнения регрессии зависимости производительности труда у от стажа работы х по данным табл. 4. (10 рабочих одной бригады заняты производством радиоэлектронных изделий, данные ранжированы по стажу их работы). Исходя из экономических соображений стаж работы выбран в качестве независимой переменной х. Сопоставление данных параллельных рядов признаков х и у показывает, что с возрастанием признака х (стажа работы), растет, хотя и не всегда, результативный признак у (производительность труда). Следовательно, между х и у существует прямая зависимость, пусть неполная, но выраженная достаточно ясно. Таблица 13 Распределение рабочих бригады по выработке и стажу работы
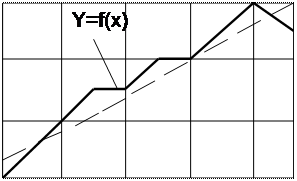
Для уточнения формы связи между рассматриваемыми признаками используем графический метод. Нанесем на график точки, соответствующие значениям х, у, получим корреляционное поле, а соединив их отрезками, — ломаную регрессии* (рис. 3). Анализируя ломаную линию, можно предположить, что возрастание выработки у идет равномерно, пропорционально росту стажа работы рабочих х. В основе этой зависимости в данных конкретных условиях лежит прямолинейная связь (см. пунктирную линию на рис. 3), которая может быть выражена простым линейным уравнением регрессии: где Данный метод эффективен лишь при небольшом объеме совокупности и достаточно тесной связи между признаками. Более наглядную характеристику связи можно получить, построив ломаную регрессии по частным средним.
1 3 5 7 9 х, годы Рис.3. Зависимость выработки одного рабочего у от стажа работы х (по данным табл.13) Пользуясь расчетными значениями (табл. 13), исчислим параметры для данного уравнения регрессии: Следовательно, регрессионная модель распределения выработки по стажу работы для данного примера может быть записана в виде конкретного простого уравнения регрессии: Это уравнение характеризует зависимость среднего уровня выработки рабочими бригады от стажа работы. Расчетные значения у, найденные по данному уравнению, приведены в табл.1. Правильность расчета параметров уравнения регрессии может быть проверена сравнением сумм итогов граф по у и У табл.13 (при этом возможно некоторое расхождение вследствие округления расчетов). ◄ 4.2. ПРОВЕРКА АДЕКВАТНОСТИ РЕГРЕССИОННОЙ МОДЕЛИ Для практического использования моделей регрессии большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным. Корреляционный и регрессионный анализ обычно (особенно в условиях так называемого малого и среднего бизнеса) проводится для ограниченной по объему совокупности. Поэтому показатели регрессии и корреляции — пара метры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить насколько эти показатели характерны для всей генеральной совокупности, не являются ли они результатом стечения случайных обстоятельств, необходимо проверить адекватность построенных статистических моделей. При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют, на сколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин. Рассмотрим t-критерий Стьюдента. Значимость коэффициентов простой линейной регрессии (применительно к совокупностям, у которых n tтабл. В таком случае практически невероятно, что найденные значения параметров обусловлены только случайными совпадениями.
│►13. Для проверки значимости коэффициентов регрессии исследуемого уравнения Рассмотрим вспомогательную таблицу (табл. 14). Расчетные значения, необходимые для исчисления
Средние квадратические отклонения (табл. 14): Расчетные значения t-критерия Стьюдента: По таблице распределения Стьюдента для Поскольку расчетное значение tрасч>tтабл, оба параметра а0, а1 признаются значимыми по величине). ◄ Можно провести экономическую интерпретацию параметров уравнения регрессии После проверки адекватности, установления точности и надежности построенной модели (уравнения регрессии) ее необходимо проанализировать. Прежде всего, нужно проверить согласуются ли знаки параметров с теоретическими представлениями и соображениями о направлении влияния признака-фактора на результативный признак (показатель). В Из уравнения следует, что возрастание на 1 год стажа рабочего приводит к увеличению им дневной выработки в среднем на 0,6 изделия (величина параметра а1). Для удобства интерпретации параметра а1 используют коэффициент эластичности. Он показывает средние изменения результативного признака при изменении факторного признака на 1% и вычисляется по формуле, %: В рассматриваемом примере Следовательно, с возрастанием стажа работы на 1% следует ожидать повышения производительности труда в среднем на 0,45%. Этот вывод справедлив только для изучаемой совокупности рабочих при конкретных условиях работы. Если данная совокупность и условия работы типичны, то коэффициент регрессии может быть использован для нормирования и планирования производительности труда рабочих этой профессии. Имеет смысл вычислить остатки Анализируя остатки, можно сделать ряд практических выводов. Значение остатков (табл. 7) имеют как положительные, так и отрицательные отклонения от ожидаемого уровня анализируемого показателя. Экономический интерес представляют выработки рабочих, обозначенные номерами: 5; 1; 4; 8; 7, поскольку их выработки отличаются наибольшими отклонениями. Тем самым выявляются передовые рабочие – номера 1; 8; 7, обеспечивающие наибольшее повышение средней выработки (наибольшие положительные остатки) и отстающие, требующие особого внимания рабочие – номера 5, 4 (наибольшие отрицательные остатки). В итоге положительные отклонения выработки большинства рабочих уравновешиваются отрицательными отклонениями небольшого числа рабочих, т.е. Дата добавления: 2014-12-23 ; просмотров: 206 ; Нарушение авторских прав Видео:Множественная регрессияСкачать  Построение линейной однофакторной регрессионной модели зависимости результативного признака Y от фактора Х.Линейное однофакторное уравнение регрессии имеет вид: Коэффициенты уравнения регрессии вычисляются по формулам: Для расчета коэффициентов строится вспомогательная табл.2.2 (расчеты проведены с применением пакета MS Excel): Расчетная таблица для построения и анализа Линейной модели парной регрессии
Расчет коэффициентов уравнения регрессии на основе данных табл.2.2: Вывод. Линейная регрессионная модель связи изучаемых признаков имеет вид уравнения Коэффициент регрессии 3. Проверка уравнения регрессии на адекватность[2]. 1. Оценка практической пригодности построенной модели связи Расчет R 2 : Вывод. Критерий практической пригодности модели связи R 2 > 0,5 не выполняется. Однако поскольку значение R 2 практически совпадает с 0,5, можно считать, что построенное регрессионное уравнение в достаточной мере отражает фактическую зависимость признаков и пригодно для практического применения. 2. Оценка статистической значимости (неслучайности) коэффициента R 2 по F-критерию Р.Фишера рассчитывается по формуле: где m – число коэффициентов уравнения регрессии (параметров уравнения регрессии), n- число наблюдений. Расчет значения F при n=30, m=2: Табличное (критическое) значение F-критерия Fтабл имеет общий вид Так как Fрасч>Fтабл, то величина найденного коэффициента детерминации R 2. признается неслучайной с вероятностью 0,95. Вывод. Построенное уравнение регрессии можно считать адекватным с надежностью 95%. 📹 ВидеоМножественная регрессия в ExcelСкачать  Эконометрика Линейная регрессия и корреляцияСкачать  Что такое линейная регрессия? Душкин объяснитСкачать  Эконометрика. Построение модели множественной регрессии в Excel. Часть 1.Скачать  Парная регрессия: линейная зависимостьСкачать  Точечный прогноз. Интервальный прогноз. Построение уравнения регрессии с помощью анализа данныхСкачать  Линейная регрессияСкачать  Математика #1 | Корреляция и регрессияСкачать  Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать  Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать  Корреляционно-регрессионный анализ многомерных данных в ExcelСкачать  Построение уравнения линейной регрессии методом наименьших квадратов.Скачать  Множественная регрессия в Excel и мультиколлинеарностьСкачать  Линейная регрессия в Python за 13 МИН для чайников [#Машинное Обучения от 16 летнего Школьника]Скачать ![Линейная регрессия в Python за 13 МИН для чайников [#Машинное Обучения от 16 летнего Школьника]](https://i.ytimg.com/vi/y--76SrfRm8/0.jpg) Эконометрика. Построение модели множественной регрессии в Excel.Скачать  Практика Многофакторная регрессияСкачать  Эконометрика. Множественная регрессия и корреляция.Скачать  Линейная парная регрессия в Eviews(англ.интерфейс)Скачать  |
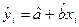
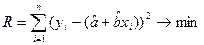
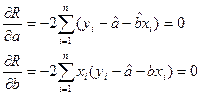
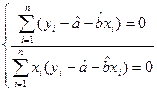
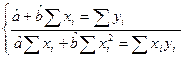
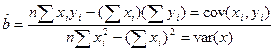
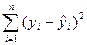
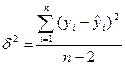
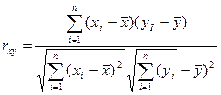
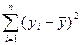
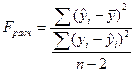
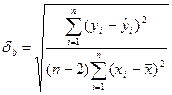
 (46)
(46)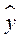 — теоретические значения результативного признака, полученные по уравнению регрессии;
— теоретические значения результативного признака, полученные по уравнению регрессии;  ,
, 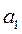 — коэффициенты (параметры) уравнения регрессии.
— коэффициенты (параметры) уравнения регрессии. от выравненных
от выравненных 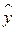 :
: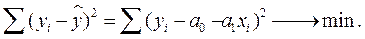 (47)
(47)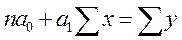 ; (48)
; (48)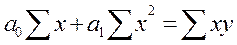 .
. ; (49)
; (49) . (50)
. (50)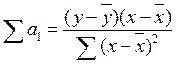 , (51)
, (51)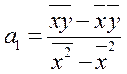 , (52)
, (52)
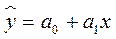 , находим значения
, находим значения 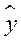 , зависящие только от заданного значения х [6].
, зависящие только от заданного значения х [6].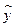
 =55
=55 =73
=73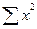 =385
=385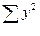 =565
=565 =451
=451
 — теоретические расчетные значения результативного признака (выработки одного рабочего, шт.), полученные по уравнению регрессии; а0,а1 — неизвестные параметры уравнения регрессии; х — стаж работы рабочих, годы.
— теоретические расчетные значения результативного признака (выработки одного рабочего, шт.), полученные по уравнению регрессии; а0,а1 — неизвестные параметры уравнения регрессии; х — стаж работы рабочих, годы.
 ;
;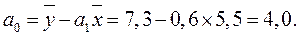


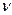 =10-2 = 8 степенями свободы.
=10-2 = 8 степенями свободы. ,
, 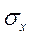

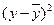


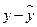




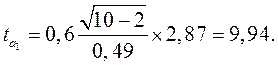
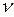 =8 находим критическое значение t-критерия: (tнабл=3,307 при α=0,05).
=8 находим критическое значение t-критерия: (tнабл=3,307 при α=0,05).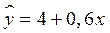 , характеризующем зависимость выработки за смену рабочим у от стажа работы х, параметр а1>0. Следовательно, с возрастанием стажа выработка увеличивается.
, характеризующем зависимость выработки за смену рабочим у от стажа работы х, параметр а1>0. Следовательно, с возрастанием стажа выработка увеличивается. (57)
(57) .
.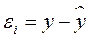 , характеризующие отклонение i-х наблюдений от значений, которые следует ожидать в среднем.
, характеризующие отклонение i-х наблюдений от значений, которые следует ожидать в среднем. .
.

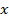






 0,245
0,245 = 2184,9-0,245∙2321,67=1616,091
= 2184,9-0,245∙2321,67=1616,091
 показывает, что при увеличении факторного признака Выручка от продажи продукциина 1 млн руб. значение результативного признака Прибыль от продажи продукции увеличивается в среднем на
показывает, что при увеличении факторного признака Выручка от продажи продукциина 1 млн руб. значение результативного признака Прибыль от продажи продукции увеличивается в среднем на  млн руб.
млн руб. по величине коэффициента детерминации R 2.
по величине коэффициента детерминации R 2.

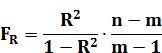
 = 27,888
= 27,888 , где
, где  — уровень значимости, m– число коэффициентов уравнения регрессии. При уровне значимости
— уровень значимости, m– число коэффициентов уравнения регрессии. При уровне значимости  0,05 и m=2
0,05 и m=2

